超效率数据包络分析模型在装备维修保障方案评估中的应用

王秀华 ，　李忠光，　何志桂

(1. 装备学院 研究生管理大队， 北京 101416； 　2. 66186部队)

超效率数据包络分析模型在装备维修保障方案评估中的应用

王秀华1，李忠光1，何志桂2

(1. 装备学院 研究生管理大队， 北京 101416； 2. 66186部队)

摘要针对传统数据包络分析方法在方案评估中不能对多个有效决策单元进一步排序的问题，采用超效率数据包络分析对装备维修保障方案进行评估。分析构建了评估指标体系，建立了基于超效率数据包络分析的装备维修保障方案评估模型；运用MATLAB编程，得到各方案的目标函数值θ*，依据θ*值大小对装备维修保障方案的优劣进行排序，并对无效方案提出改进办法。实际应用表明了方法的有效性。

关键词数据包络分析；超效率数据包络分析；装备维修；保障方案；评估

为保证装备维修保障工作及时高效进行，各级保障部门都要制定装备维修保障方案，以完成遂行装备保障任务与年度维修保障计划。装备保障单位执行装备保障任务时可能有多个保障方案，因此对装备维修保障方案的评估与选择成为装备保障的重要内容之一。对装备维修保障方案进行评估，是为了尽可能地反映方案的客观内容，考查方案完成任务的效率，并对多个方案进行排序优选，寻找装备维修保障资源分配中存在若干问题，为科学制订装备维修保障方案，优化资源配置与结构，提高装备保障能力提供借鉴。目前常见的装备维修保障方案评估方法诸如层次分析法、模糊综合分析法、灰色关联分析法、神经网络分析法、主成分分析法等，这些方法在权重的确定上有很大的主观色彩，导致结果的不稳定和可信度降低[1]。

美国著名运筹学家Charnes等[2]所提出的数据包络分析(DEA)方法，是利用经济活动中决策单元投入与产出之间的比率进行相对效率分析的常用研究方法。其变量是各投入产出项的权重，不需要人为给定，确保了评估结果更客观实际，特别适用于多投入和多产出方面的评估分析。DEA方法被广泛应用于众多领域和行业，目前已延伸到很多非盈利性质的单位。近年来，数据包络方法在装备领域中的应用研究也越来越多，如装备研制规划方案的评估[3]、装备保障方案的评估[4]、装备维修保障系统效能的评估[5]等。

1装备维修保障方案评估指标

装备维修保障方案是装备维修机构根据作战及其他军事行动任务要求，为组织实施装备维修保障而制定的行动设想。维修活动的进行离不开保障资源，如人员的技术水平与数量、维修器材的数量与种类，以及与之相关的费用。从经济学的角度讲，有投入就有产出，也就有投入与产出的比较与衡量，即如何分配资源能够获得较大产出，或在产出一定的前提下力求投入较少。在这里，投入用及时性和经济性指标来描述，产出则用有效性指标来描述，如表1所示。

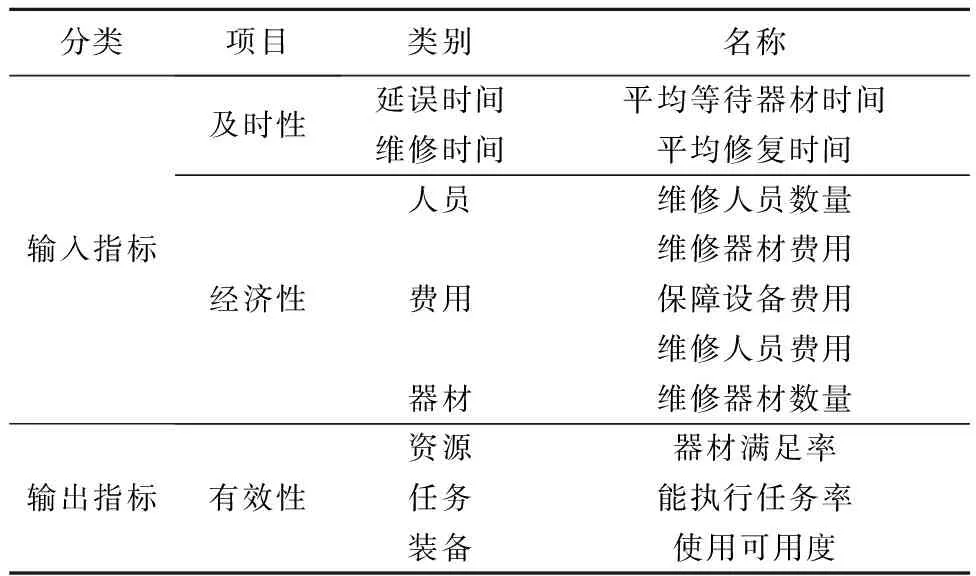
表1　评估指标

1.1及时性

及时性，用来衡量完成装备保障任务的效率，包括维修时间和延误时间两部分。维修时间指恢复装备功能要求的时间长度[6]。本文中，维修时间是指部队进行的预防性维修时间和修复性维修时间，用平均修复时间来度量。延误可能是由于保障机构的组织管理因素或资源缺乏等造成装备无法按时维修，在这里延误时间主要是指在维修过程中因为器材短缺而造成维修活动中断的延误，用平均等待器材时间来度量。

1.2经济性

经济性，主要是指维修保障资源的投入特性，即人、财、物等。人是指直接参加维修保障活动的人员数量，不包括管理机构的人员。财主要是指进行维修保障活动所花费的物质、人员等费用，物在这里主要考虑进行装备维修活动所使用的各类维修器材的数量。

1.3有效性

有效性，即完成装备维修活动的效率特性。装备维修保障方案是否有效还应考虑该方案完成任务的能力，只有最大限度地完成装备维修保障任务才具有更高的保障能力，衡量指标如器材满足率、能执行任务率、使用可用度等。

2DEA与超效率DEA评估模型

2.1DEA模型

根据DEA评估的思想，将各维修保障方案作为DEA模型中的决策单元(Decision Making Units,DMU)。现假设有n个方案DMUj，j=1,2,3,…,n，构造规模收益固定的评估模型CCR[7-8](Charnes,Cooper and Rhodes)：

minθ

(1)

式中，θ为效率值；Xj为第j个投入指标；Yj为第j个产出指标；S-和S+为松弛变量；λj为权系数。根据上式得到的第j个方案结果记为θ*，S*-和S*+，据此判断其DEA有效性如下：

1) 若θ*=1，且S*-=0,S*+=0，则DMUj为DEA有效，表示在这n个方案中，此时的输入Xj能够获得最大的产出Yj；

2) 若θ*=1，至少有某个S*->0或S*+>0，则DMUj为弱DEA有效，表示在这n个方案中，可以通过减少投入或增加产出来改进方案;S*->0表示方案DMUj的某投入指标没有充分利用；S*+>0表示方案DMUj的产出指标不是最佳的，还可以增加产出而使投入不变。

3) 若θ*<1，则DMUj为DEA无效，这表明需改进保障方案，可以通过减少人员、费用、器材的投入或提高器材满足率等使方案趋于有效。

2.2超效率DEA模型

运用CCR模型进行评估时常常会遇到一个棘手问题，即多个有效的决策单元并存。如何对效率值均为1的多个决策单元进行区分，引起了许多学者的关注。1993年Andersen和Petersen提出了超效率DEA模型[9]。超效率DEA的主要内涵是对决策单元进行评估时，约束条件不包括其本身，使得有效的决策单元构成的生产前沿面随之变化，而无效决策单元的效率值和CCR模型计算结果是一致的。因此，运用超效率DEA模型能够克服CCR模型的弊端，实现所有决策单元的优劣排序问题[10]。超效率DEA模型如下：

minθ

(2)

该模型中变量的含义与CCR模型一致。从模型中可以看出，当对第j0个方案进行效率值计算时，其不包括在约束条件中，这是超效率模型与CCR模型的最主要区别。

3评估应用

某型装备执行一次军事训练任务，其装备维修保障方案有10个，每个保障方案的投入产出指标值如表2所示，对这10个装备维修保障方案效率进行评估。X1，X2，X3，X4，X5，X6，X7分别表示平均等待器材时间、平均修复时间、维修人员数量、维修器材费用、保障设备费用、维修人员费用、维修器材数量。Y1，Y2，Y3分别表示器材满足率、能执行任务率、使用可用度。运用前文建立的模型对该案例进行分析求解。利用CCR模型求解各方案的综合效率、技术效率和规模效率。通过分析各方案的投入冗余量和产出不足量，为DEA无效方案提出改进方向；利用超效率DEA模型计算效率值并排序，效率值越高，投资方案越优，进而寻得最佳保障方案。

表2　投入产出指标

3.1DEA有效性分析

运用MATLAB 7.14进行编程，求解模型(1)，得到各方案效率值，如表3所示。

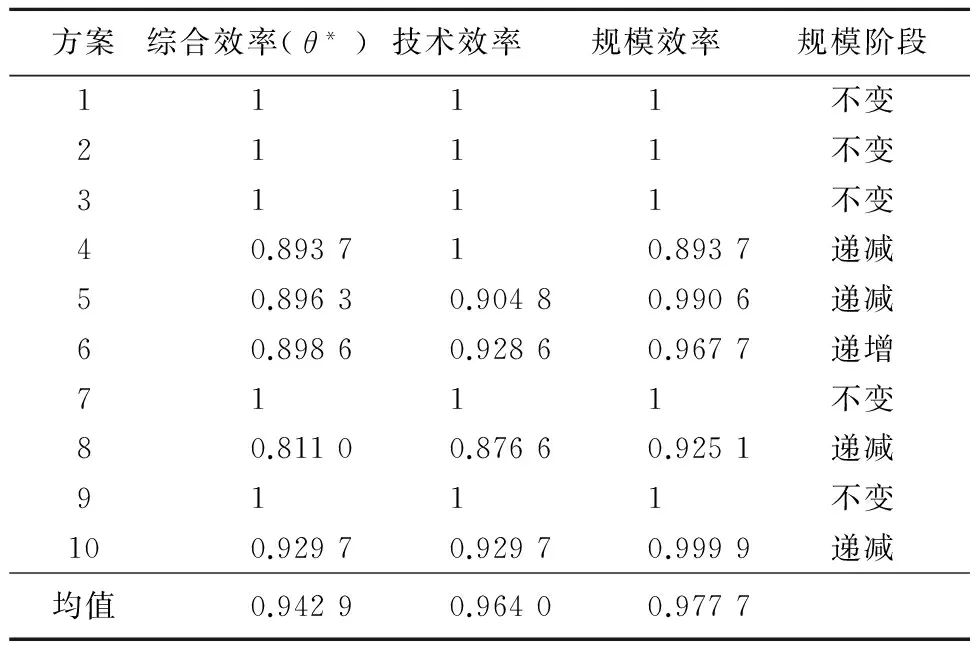
表3　CCR模型效率值

从表3可以看出，上述10个装备维修保障方案的综合效率平均值为0.942 9。DEA有效与无效装备维修保障方案各有5个，分别占方案总数的50%，可见这5个装备维修保障方案还需要进一步提高。1、2、3、7、9这5个有效方案均处在规模效率不变的阶段，说明这5个方案资源利用相对合理，可以采纳。对于4、5、6、8、10这5个无效方案，只有方案4的技术效率是有效的，表明这个方案的无效是由于规模非有效导致的，要改善方案4的保障水平，可以增加规模投入。

3.2保障方案优劣排序

如表3所示，对于用DEA求出的方案效率值中，有5个方案都是有效的，它们的综合效率(θ*)都为1，不能进一步辨别出这5个方案的相对差异。因此，需要运用超效率DEA模型计算效率值θ*。将数据代入模型(2)，结果如表4所示。θ*效率值越高，方案的有效性会随之提高，是DEA选择方向。

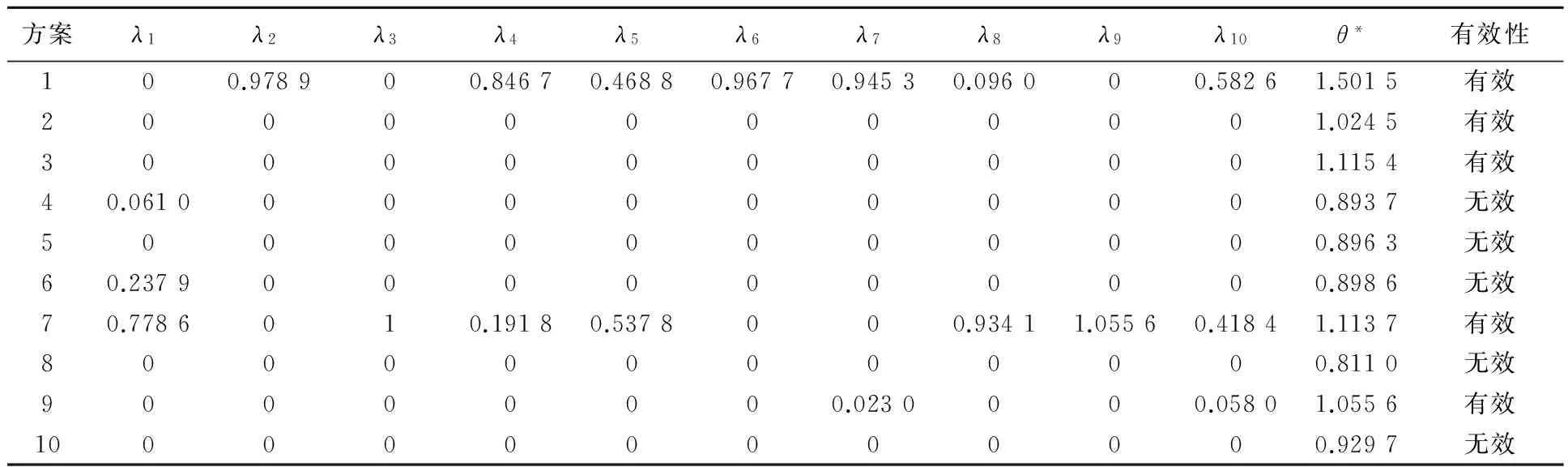
表4　各DEA效率值运算结果

从表4可以看出方案1、2、3、7、9这5个方案是有效的，其余5个方案是无效的，与DEA模型所得的结果一致。最终这10个方案的排序为：DMU1≫DMU3≫DMU7≫DMU9≫DMU2≫DMU10≫DMU6≫DMU5≫DMU4≫DMU8。

3.3无效方案的改进

与方案4不同的是，方案5、6、8、10这4个方案的技术效率和规模效率都小于1，可见这4个方案的DEA无效是由于技术和规模共同导致的。因此，要使这些方案有效，既要考虑调整投入规模也要考虑提高技术效率。对于这5个无效方案，可以通过寻找DEA相对有效前沿面上的投影调整。设S*+,S*-,θ*为模型(1)的最优解。令

(3)

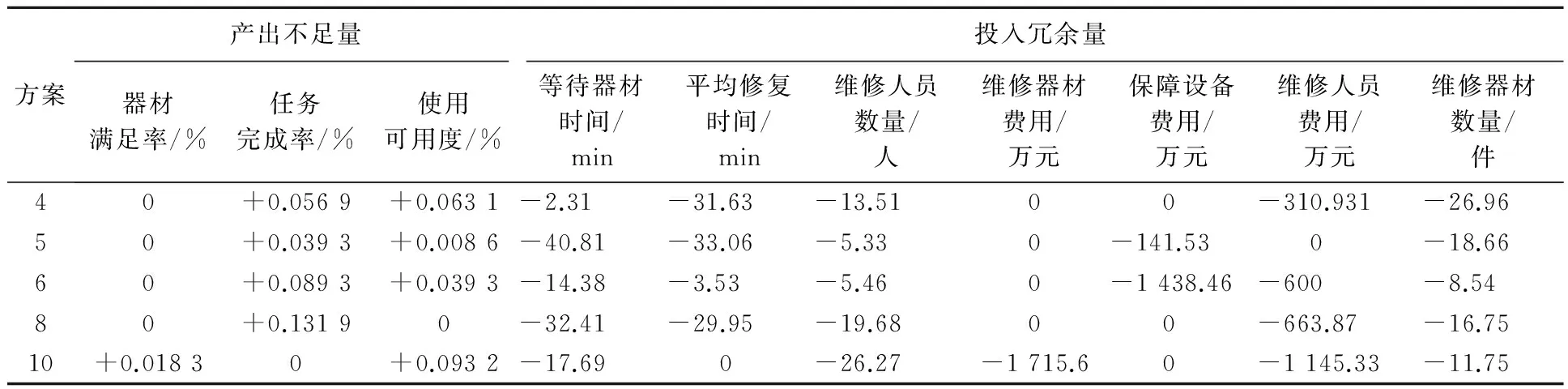
表5　无效方案产出不足和投入冗余

投影值是保障方案效率处于最优状态下投入与产出指标所对应的数值。“+”表示需要增加的产出量，“-”表示需要减少的投入量，“0”表示不需要调整的量。通过表5可以分析无效方案的调整方向和规模，如方案5在投入和产出方面均存在不同程度地浪费和不足。若要使方案5有效，则可以节省平均等待器材时间约40 min，平均修复时间约33 min，减少维修人员数量约5人，降低保障设备费用142万元，减少投入维修器材数量约19件；若不减少投入，要想使此方案有效也可以增加产出，如任务完成率提高约4个百分比，使用可用度提高约1个百分比。另外，器材满足率不需要调整，说明即使将过剩的资源全部发挥其效率，也不会对器材满足率有明显影响，因此增加这些资源的投入显然是没有必要的。由表5可以看出，对无效方案的改进可以从投入与产出两方面着手。

4结 束 语

装备维修保障方案是确定维修资源种类与数量的基本输入信息，也是落实装备维修保障要求与实现保障目标的总体规划。对装备维修保障方案做出科学评估，是检验装备维修保障方案建设水平、保证装备维修保障工作落实的重要途径。超效率DEA是评估装备维修保障方案的有效方法，可以对多个有效的决策单元进一步分析比较，弥补了传统DEA方法的不足。

参考文献(References)

[1]刘千里，刘中昆.航空装备维修保障信息化理论与实践创新[M].北京: 蓝天出版社，2008：136-140.

[2]CHARNES A，COOPER W W.Measuring the efficiency of decision making units[J].European Journal of Operational Research，1978,2(6):429-444.

[3]曲丽丽，康锐.基于DEA的研制阶段装备保障方案评价模型[J].北京航空航天大学学报，2009,35(12):1460-1462.

[4]代海飞，刘小方，张永天, 等.基于DEA的装备保障方案评估[J].四川兵工学报，2013,34(5):58-61.

[5]王猛，陈桂明，郑钦.基于DEA的装备维修保障系统效能评估研究[J].装备指挥技术学院学报，2008,19(1):108-111.

[6]KUMAR U D.可靠性、维修与后勤保障—寿命周期方法[M].刘庆华，宋宁哲，译.北京:电子工业出版社，2010：85-86.

[7]郝海，踪家峰.系统分析与评价方法[M].北京: 经济科学出版社，2007：185-238.

[8]叶义成，柯丽华，黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社，2006：237-254.

[9]ANDERSEN P，PETERSEN N C.A procedure for ranking efficient units in data envelopment analysis[J].Management Science，1993,39(10):1261-1264.

[10]孟明强，周安会.超效率DEA模型在武器装备方案选择中的应用[J].军械工程学院学报，2014,26(1):2-4.

(编辑：李江涛)

Application of SE-DEA model on the Equipment Maintenance Support Scheme Evaluation

WANG Xiuhua1，LI Zhongguang1，HE Zhigui2

(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China;2. 66186 Troops, China)

AbstractTo tackle the issue that traditional data envelopment analysis cannot further sort multiple effective decision units in the scheme evaluation, the paper conducts evaluation on the equipment maintenance support plan with super efficiency data envelopment analysis (SE-DEA). The analysis is used to build up an evaluation indicator system and then an equipment maintenance support scheme based on super efficiency data envelopment analysis; it draws the objective function value of each scheme by MATLAB programming. The paper also sorts the equipment maintenance support schemes according to the advantages and disadvantages in terms of value and proposes improvement approaches for ineffective schemes. The practical applications demonstrate the effectiveness of the approaches.

Keywordsdata envelopment analysis (DEA); super efficiency data envelopment analysis; equipment maintenance; support scheme

收稿日期2015-10-10

基金项目部委级资助项目

作者简介王秀华(1977-)，女，讲师，博士研究生，主要研究方向为装备保障与指挥。wangxiuhuade1@163.com

中图分类号E92

文章编号2095-3828(2016)03-0050-05

文献标志码A

DOI10.3783/j.issn.2095-3828.2016.03.010