捕食与被捕食模型的研究进展

吴楚芬，柯　妍佛山科学技术学院数学与大数据学院，广东佛山　528000



捕食与被捕食模型的研究进展

吴楚芬，柯妍
佛山科学技术学院数学与大数据学院，广东佛山528000

摘要自然界中的生态关系错综复杂，最为常见的一类系统是捕食与被捕食模型。本文讨论了捕食与被捕食模型其功能反应函数的研究进展。

关键词捕食与被捕食；模型；功能反应

“物竞天择，适者生存”是生物进化论里的生存模式。生态系统中生物的演变过程漫长而复杂，而捕食与被捕食这种生物行为是一种较为普遍的现象。捕食现象随处可见，众多种群是如何演变至今？遵循何种规律？动物的增长为何未引起整个生物界混乱？动物受到何种制约条件？生物系统的平衡，种群之间是如何维持的，种群的持久性又涵盖了什么规律。这一系列的问题，吸引了很多学者深入地去研究，用数学式子把它们的变化规律罗列出来。

早在1838年，生物数学家P.F.Verhulst基于前人A.L.J.Quetelet的工作，发现生物增长过程中有阻抗因素后，提出了著名的Logistic方程［1］。P.F.Verhulst 对Malthus模型：

进行了修改，从而得到Verhulst模型：

在（1）、（2）中，t表示时刻，x表示种群密度，r表示相对增长率，模型（2）即是著名的Logistic方程，其主要描述种群增长走势，K表示环境容纳量，也称之为系统的承受能力。

在20世纪Lotka和Volterra开始研究捕食与被捕食模型，即著名的L-V模型［2，3］：

其中，r1为食饵的增长率，r2为捕食者的死亡率，l1， l2表示捕食关系。L-V模型提出之后，很多科学家发现模型虽然解释了大量捕食现象，但是在某些情况下实验结果和理论相差甚远。随后许多科学家对模型进行了改进与定性分析，使得模型更加贴近现实生活。本文从具有功能反应的捕食与被捕食模型出发，分析捕食与被捕食模型的研究进程。

1　具有功能反应的捕食与被捕食模型的数学分析

1.1具有功能反应的捕食与被捕食模型的建立和发展

20世纪20年代，生物学家U.D’Ancona发现，第一次世界大战期间，在地中海周边的码头口岸捕捉回来的几类鱼群中，它们各自所占的百分比较平常时期有所变化，鲨鱼等一系列捕食者所占的比例都明显增长了。他认为，在第一次世界大战时期，渔民作业少，对鱼类的捕捉量大幅度下降，导致海域中的被捕食鱼类增加，随之增加的也有作为捕食者的鱼类。第一次世界大战过后，渔民在海域里频繁地作业，被捕食者鱼类数量逐渐减少，捕食者鱼类也减少，但是U.D’Ancona在数据中发现一个问题，为什么鲨鱼在鱼类总量中所占的比例会上升呢？由此他就去拜访了数学家V.Volterra。

V.Volterra开始思考研究种群数量的变化，Volterra假设，若不存在捕食者、食饵时，种群的增长就符合Malthus方程（1）；而若捕食者存在时，在一定单位时间内每一个捕食者对食饵的捕食量与食饵种群数目成正比，设比例常数为l ，即有：

在（3）式中，x， y 分别表示食饵和捕食者的数量。若再假设捕食者捕食完食饵后，忽略时间滞后的作用，马上转化为能量，给捕食种群提供营养繁殖，设转化系数为α，又设捕食者的死亡率为a ，从而有：

结合以上式子（3）和（4），Volterra得到了由捕食者与食饵两个种群相互作用制约的数学模型，即L-V模型：

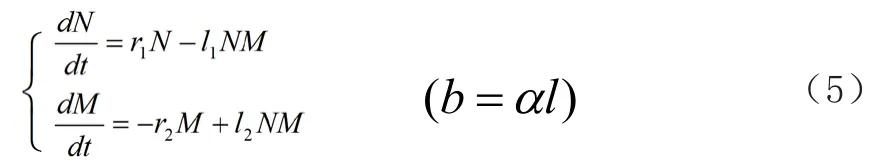
经典的L-V模型成功地阐释了当时生物学家没有办法解决的疑问，但也有一些缺陷，如线性关系的死亡率，从而使得理论数据与现实数据相差甚远，为了模型可以更加完美实用，不少学者都试图对模型进行修正。经典的L-V模型被推广到如下的具有功能性反应函数的捕食与被捕食模型：

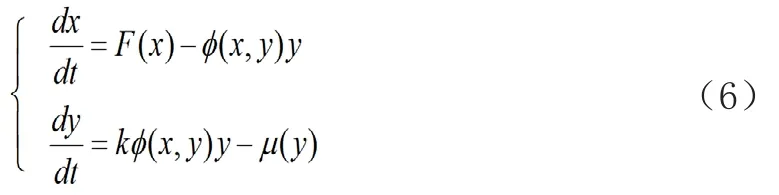
在（6）中，F（x）为食饵在没有捕食者出现时的增长率，φ（x，y）为捕食者的功能反应函数，µ（y）为捕食者的死亡率。模型（6）中，起到关键作用的是功能性反应函数、被捕食者的增长函数和捕食者的死亡率函数，所以学者们围绕这3个方面对L-V模型进行分析。

1.2功能性反应函数的分析讨论

功能反应包含2个方面，食饵依赖型、捕食者依赖型的反应函数。在一开始人们多局限于研究食饵依赖型功能反应。

当食饵的数量无限增多的时候，捕食者并非一味地成正比例增加，而是达到一定程度，会出现缓慢的增长甚至出现停止增长的情况，就如同出现了环境最大容纳量一样。此时，科学家Holling和Watt开始研究其中的原因，提出一个新的关系，他们认为食饵数量增加的时候，捕获率应该由一开始的线性上升直到一个稳定的状态，到达一个捕获的最高水平。他们在否定了L-V模型中简单的线性关系的同时提出了Holling型功能反应函数。在1965年，Holling［4］在实验研究的基础上，对不同种群的捕食者提出了3种不同的功能反应。

第一种是对滤食性动物（软体动物）、大型藻类和酵母的取食过程研究，发现捕食过程都显示出明显的饱和度，增长都趋向于一个定值，把此类情况称为HollingⅠ类功能反应函数。

对于无脊椎动物的实验情况分析，捕食者的捕获率是随着食饵数量的增加而上升的，一直上升到一个饱和水平，当食物足够多时，捕食者的饥饿感降低导致捕获率下降，把此类情况称为HollingⅡ类功能反应函数。

对于脊椎动物的观察研究发现，在食物比较少的时候，动物会去观察然后有方法地捕食，随着食物数量增大捕获率加速增大，当食物数量增多到一定程度时，捕食者的饥饿感减弱捕获率减少，最后达到饱和状态，把此类情况称为HollingⅢ类功能反应函数。

又由于空间都是有限的、食物也会变得少，所以种群内就会发生斗争，斗争导致种群数量下降，然而以上的3个Holling型功能反应函数所表现出来的模型都是在第一象限的单调函数有违实际情况，实际上功能反应函数并非都单调的。在微生物动力学中会出现抑制现象，人口动力学中出现群体御防现象，所以Andrews在文献［5］中提出HollingⅣ类功能反应函数。

依赖于捕食者的功能反应函数，这是一直被学者们忽略的内容。上述的Holling类功能反应函数在捕食与被捕食模型中起着决定性的作用，但是不能否定的是，食饵功能反应函数还不能全面的概括生物的功能反应。当环境变得恶劣时，物种会选择迁徙，当同类太多而食物不足时，种群内就会发生斗争，从而导致群内数量下降。所以在食物充足时，食饵依赖型功能反应函数可以满足现实中的模型增长，食物不足导致种群内部斗争时就要考虑捕食者依赖型功能反应函数。

1955年，科学家Watt通过大量的研究，最终得出了这样一个结论：捕食者的捕食效率是随着捕食者的密度增大而降低的。于是，他提出了2类捕食者依赖型功能反应函数［6］：和

1969年，科学家Hassell和Varlay［6］考虑到捕食者们的相互干扰因素，提出了新的一类捕食者功能反应：φ（x ，y）=pxy-m，0＜m≤1。

1975年，科学家Beddington和DeAngelis［6］指出，捕食者不但要寻找食物，还有处理好与其他种群内捕食者之间的竞争，以至于捕食效率下降，于是，他提出了B-D功能反应函数：

比率依赖型功能反应函数可以认为是食饵种群和捕食者种群的数量（密度）比值的函数。最初提出该理论的是Arditi和Ginzburg，随后很多学者们都展开了研究，最后得到的比率型功能反应表达式如下［6］：

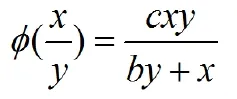
功能性反应函数其类型的不断增加与修正，使得食饵-捕食者系统的应用范围越来越广阔。

参考文献

［1］P.F.Verhulst，Notice sur la loi que la population suit dans son accroissement［J］，Corr. Math. Phys.，1838， 10： 113-121.

［2］A.J. Lotka， Elements of Physical Biology［M］. New York：Williams and Wilkins， 1925.

［3］V. Volterra， Variazionie fluttuazioni del numero d’individui in specie animali conviventi ［J］ ，Men. Acad. Licei.，1926，2 ：31-113.

［4］C.S. Holling， The functional response of predators to prey density and its role in mimicry and population regulation ［J］， Mem. Ent. Soc. Can. 1965， 45： 1-60.

［5］J.F. Andrews， A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates［J， Biotechnol. Bioeng.，1968，10：707-723.

［6］陆征一，王稳地.生物数学前沿［M］.北京：科学出版社，2008.

中图分类号Q-3

文献标识码A

文章编号1674-6708（2016）165-0159-02

基金项目：广东省教育厅教学研究课题：理论与建模相结合的《常微分方程》实践教学（gj41209）。

作者简介：吴楚芬，副教授，研究方向为微分方程理论及应用。