同时考虑实际气体效应和滑移流效应螺旋槽干气密封性能分析

宋鹏云，张帅，许恒杰（昆明理工大学化学工程学院，云南 昆明 650500）



同时考虑实际气体效应和滑移流效应螺旋槽干气密封性能分析

宋鹏云，张帅，许恒杰
（昆明理工大学化学工程学院，云南 昆明 650500）

摘要：为分析考虑实际气体效应和滑移流效应的螺旋槽干气密封性能，通过维里实际气体状态方程代替理想气体状态方程、有效黏性系数代替动力黏度修正窄槽理论螺旋槽干气密封气膜压力控制方程。以氮气（N2）、氢气（H2）、二氧化碳（CO2）为例，分别计算、对比无滑移理想气体、滑移理想气体、无滑移实际气体、滑移实际气体时螺旋槽干气密封的泄漏率、槽根处压力、端面开启力。结果表明：滑移流效应使气体泄漏率增大、槽根处压力和端面开启力降低；实际气体效应使易受压缩气体（压缩因子Z＜1）的泄漏率、槽根压力、端面开启力增大，使不易受压缩气体（压缩因子Z＞1）泄漏率、槽根压力、端面开启力减小。随着气体压力增大，滑移流效应逐渐减弱，而实际气体效应增强；低压下滑移流效应起主导作用，高压下实际气体效应起主导作用。

关键词：干气密封；螺旋槽；滑移流；实际气体；窄槽理论；二氧化碳

2015-08-31收到初稿，2015-12-31收到修改稿。

联系人及第一作者：宋鹏云（1963—），男，教授。

Received date: 2015-08-31.

Foundation item: supported by the National Natural Science Foundation of China (51465026).

引　言

干气密封的气膜厚度很小，气体润滑中气体分子平均自由程与气膜厚度之比处于0.01～0.1之间时，一般需要考虑滑移流效应的影响[1]。目前对螺旋槽干气密封的研究国内外已有诸多报道。Ruan[2]基于有限单元法研究螺旋槽干气密封性能，发现在低速低压工况下，不能忽略滑移流效应的影响。丁雪兴等[3-4]利用PH线性化方法，将非线性雷诺偏微分方程转化成线性偏微分方程，引入复函数将复常数偏微分方程分为两个线性实常数方程，迭代求解分析受滑移流影响的螺旋槽干气密封性能和螺旋槽干气密封润滑气膜角向涡动的稳定性。尹晓妮[5]利用三角形单元形函数有限元分析了低速低压下螺旋槽干气密封受滑移流效应影响的情况。许静等[6-7]同时考虑微尺度效应和热黏效应，利用有限元法研究了滑移流效应和热黏度效应对干气密封的影响。蒋小文等[8]、彭旭东等[9]对螺旋槽干气密封的主要性能参数进行了分析。宋鹏云等[10]采用有效黏性系数的概念，对受滑移流影响的螺旋槽干气密封性能进行解析分析。这些研究都将气体视为理想气体，而随着压力的升高，实际气体效应会偏离理想气体，在一些工况下是无法忽视的。

本文提出了一种同时考虑滑移流效应和实际气体效应影响的螺旋槽密封性能的解析算法，并与不考虑滑移流效应和实际气体效应的干气密封、仅考虑滑移流效应的干气密封、仅考虑实际气体效应的干气密封进行对比分析。所选气体分别为氮气、氢气、二氧化碳。本文解析算法是通过有效黏性系数表达滑移流效应、维里实际气体状态方程表达实际气体效应对螺旋槽窄槽理论进行修正，并求解。

1　有效黏性系数

干气密封低速运转时，流体动压效应较弱，密封动环与静环间的距离很小，气膜厚度很薄，接近分子平均自由程。此时，需考虑气体的滑移流效应。滑移流现象宏观表现等效于黏度的减小。考虑滑移流效应影响的气体黏度为有效黏性系数µeff。有效黏性系数方程如下

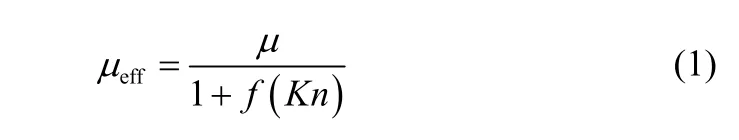
处理滑移流问题的物理模型有多种，本文选用Burgdorfer建立的一阶滑移流模型计算有效黏性系数。Burgdorfer滑移流模型下有效黏性系数µeff方程[11]为

Knudsen数描述了气体偏离连续介质的程度，定义为分子平均自由程λ与气膜厚度h的比值，即Kn=λ/h。将Kn的具体表达代入式（1）中，可获得有效黏性系数µeff与气体动力黏度µ、分子平均自由程λ、气膜厚度h之间的关系式，式（1）中的f( Kn )= 6 Kn即为式（2）。

2　考虑实际气体效应的有效黏性系数

2.1实际气体状态方程

在处理实际气体问题中，通常利用压缩因子Z来表达实际气体效应。实际气体状态方程如下

式中，Z为压缩因子，表示实际气体偏离理想气体的程度，当Z＞1时，实际气体比理想气体难于压缩；当Z＜1时，实际气体比理想气体易于压缩；当Z=1时，式（3）即为理想气体状态方程。

压缩因子Z受气体的温度、压力以及气体种类影响。本文压缩因子Z通过维里方程获得。维里方程有理论基础[12]，它利用统计力学分析分子间的相互作用力获得气体压缩因子[13]

式中，第二维里系数B可通过实验数据或Pitzer方程获得，本文依据Pitzer方程计算获得。Pitzer方程[14]表达式为

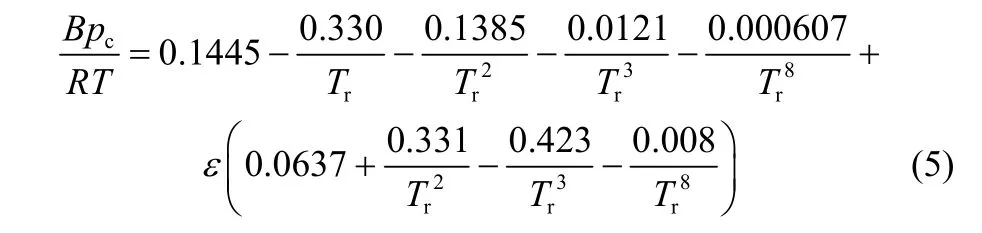
2.2实际气体分子自由程

Chapman等[15]基于气体分子的光滑刚性弹性球模型，利用气体分子在两次碰撞间动量的变化，建立了分子平均自由程λ与分子动力黏度μ、密度ρ以及平均速度之间的关系

根据Jennings[17]精确计算实际气体分子平均自由程的方法，取数值因子用实际气体状态方程式（3）替换式（6）中的气体密度ρ，联立式（4）、式（6）和式（7）可推导出干空气的实际气体分子平均自由程表达式

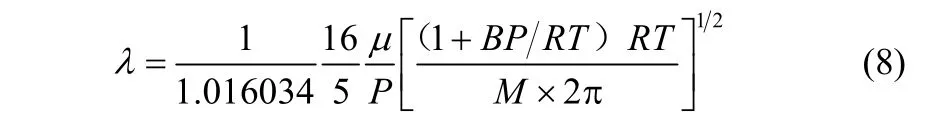
式（8）对于干空气外的其他气体依然适用。

2.3考虑实际气体效应的有效黏性系数

国内外学者对气体滑移流效应已经进行了大量研究，但大多是基于理想气体。常温、常压下，理想气体与实际气体性质较为接近，但是，随着温度降低和压力升高，实际气体和理想气体会出现差异。

将式（8）代入式（2）中，可获得实际气体的有效黏性系数

3　同时考虑实际气体效应和滑移流效应螺旋槽干气密封解析算法

3.1同时考虑实际气体效应和滑移流效应螺旋槽干气密封气膜压力控制方程

本文对螺旋槽干气密封的研究基于Muijderman的窄槽理论，根据该理论气体沿密封环径向气膜压力分布控制方程[18]为：

对于密封坝区

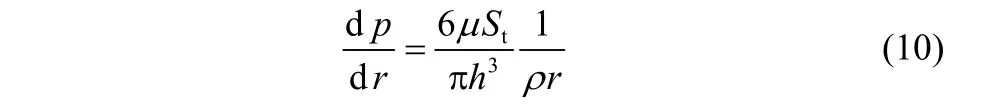
对于开有螺旋槽的槽台区

式中，g1、g2为螺旋槽系数，其具体表达分别为

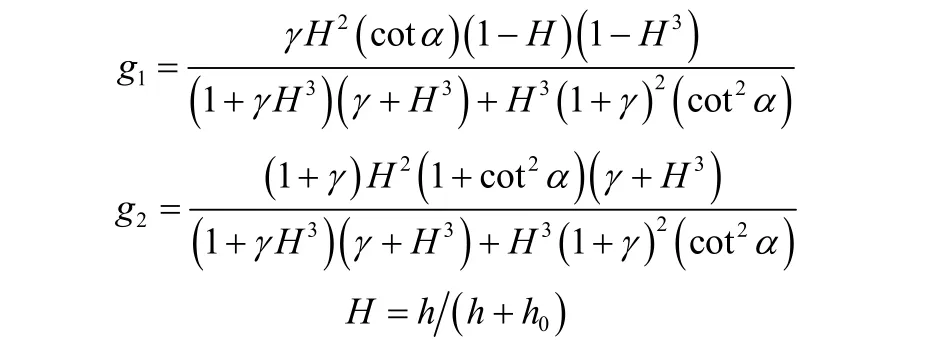
用式（3）实际气体状态方程代替式（10）、式（11）中的密度ρ，压缩因子Z由式（4）维里方程获得；用式（9）实际气体的有效黏性系数µeff代替式（10）、式（11）中的动力黏度项µ，即可获得考虑实际气体效应的低速运转下螺旋槽干气密封径向气膜压力控制方程：

对于密封坝区

对于开有螺旋槽的槽台区

3.2压力边界条件

式（12）、式（13）满足以下边界条件。在密封环内、外径处：

具体计算方法为[10]：根据质量守恒定律，通过开有螺旋槽的槽台区气体质量流量与通过密封坝区气体质量流量相等，同为St。计算时，假设质量流量St数值，利用式（12）及已知条件密封环内径处可计算出螺旋槽槽根处的压力pg，同时可获得密封坝区（ri与rg之间）的气膜压力分布p1( r )。再将所获的槽根处压力rg代入式（13）可获得外边界处压力¢，同时亦可获得槽台区（rg与ro之间）的气膜压力分布p2( r )。如果¢等于外径处的压力po，则试算结束。此时获得的压力分布p( r )即为端面气膜压力分布，泄漏率St即为端面间气体泄漏率。否则，重新假设St，重复上述试算过程，直到满足po¢= po。

通过上述反复试算，可获得端面间气体泄漏率St，槽根处压力pg。计算中常将端面间气体泄漏率质量流量St（kg·s-1）转换成标准状态下气体泄漏率体积流量Q （m3·s-1）。

3.3开启力计算

密封环动环旋转时，气体由于槽台的作用产生流体动压力，流体动压力形成了使密封环两端面分开的开启力。开启力可通过端面间气膜压力分布对端面面积积分获得。开启力F为

4　相对误差

本文基于Muijderman的窄槽理论利用式（12）、式（13）可计算获得同时考虑实际气体效应和滑移流效应螺旋槽干气密封径向压力分布p(r)，同时获得泄漏率St、开启力F。类似于式（12）、式（13），可运用窄槽理论计算获得不考虑滑移效应的理想气体相关密封性能，考虑滑移流效应的理想气体相关密封性能，不考虑滑移效应的实际气体相关密封性能。为更好地表达各因素影响，定义以下误差。

E1=[(非滑移流理想气体结果-非滑移流实际气体结果)/非滑移流实际气体结果]×100%；

E2=[(非滑移流理想气体结果-滑移流理想气体结果)/滑移流理想气体结果]×100%；

E3=[(滑移流理想气体结果-滑移流实际气体结果)/滑移流实际气体结果]×100%。

E4=[(非滑移流实际气体结果-滑移流实际气体结果)/滑移流实际气体结果]×100%。

5　算例结果分析与讨论

5.1算例

本文几何参数选择参照考虑滑移流效应螺旋槽干气密封经典算例[2]。几何参数为：内径ir=30 mm，槽根处半径rg=34.8 mm，外径ro=42 mm，螺旋槽角a=20°，槽深h0=2.5 µm，槽台宽比g1=。环境参数选取内压pi=0.1013 MPa，环境温度T=300 K。转速n=500 r·min-1。

5.2氮气密封性能计算及比较分析

5.2.1氮气第二维里系数计算在压力为0.1013 MPa，温度为300 K条件下，由《Matheson气体数据手册》[19]查得，氮气摩尔质量M=28.013 g·mol-1，临界温度Tc=126.1 K，临界压力pc=3.394 MPa，偏心因子e=0.040，动力黏度m=1.80×10-5Pa·s。由式（5）可计算获得氮气的第二维里系数B=-4.31974×10-6m3·mol-1。

5.2.2密封性能计算及比较分析选取外压po分别为低压0.202 MPa、中压4.5852 MPa、高压10 MPa进行计算分析，压力对氮气动力黏度影响忽略不计，选取不同气膜厚度计算氮气相关密封性能，计算结果绘制成曲线，如图1～图3所示。为准确表现相对误差，取气膜厚度为0.9 µm处相对误差绘制相对误差表格，如表1～表3所示。

图1　氮气泄漏率Fig.1　Leakage for N2

从图1和表1可以看出，氮气作为润滑气体时，低压、中压、高压工况下，E1、E3、E2和E4均小于零，说明滑移流效应和实际气体效应均使螺旋槽干气密封的气体体积泄漏率增大。这是由于滑移流效应宏观上等效于黏度的降低，黏度降低会导致泄漏率增大；同时氮气的第二维里系数B=-4.31974× 10-6，即压缩因子Z＜1，表明氮气实际气体比理想气体更易于压缩，在相同压力的作用下，比理想气体具有更小的体积。这样，通过同样的密封通道（间隙）时，就需要更多体积的气体，宏观表现为标准状态下气体体积泄漏率Q升高。从表1可以看出随着外压po的增加，滑移流效应是减弱的，实际气体效应是增强的。

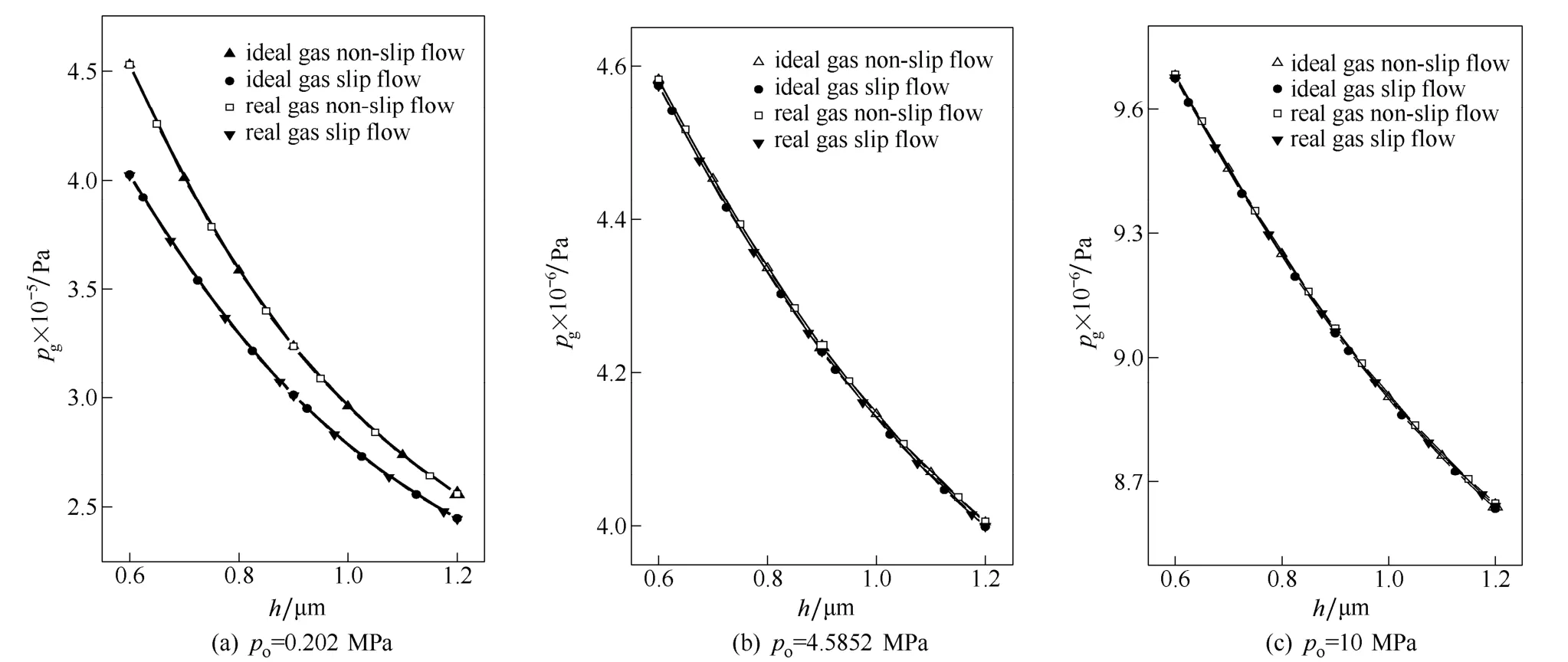
图2　氮气槽根压力Fig.2　Pressure at spiral groove root radius for N2

图3　氮气开启力Fig.3　Opening force for N2

表1　氮气泄漏率相对误差Table 1　Error of leakage for N2

表2　氮气槽根压力相对误差Table 2　Error of pressure at groove root radius for N2

表3　氮气开启力相对误差Table 3　Error of opening force for N2

图2及表2表明，槽根处压力随着气膜厚度的增大而减小。随着外压po的增大，槽根处压力受滑移流效应影响急剧减小，受实际气体效应影响而增大。就本文的计算条件而言，低压工况下，滑移流效应引起的误差最大达到7.4772%，实际气体效应在高压下引起的误差比低压下引起的误差至少大1个数量级。

图3表明，开启力随着气膜厚度的增大而减小。不考虑滑移流影响，相同压力下，氮气实际气体开启力大于理想气体，这与实际气体效应使槽根处压力增大的结果一致。不考虑实际气体效应，相同压力下，氮气受滑移流效应影响，开启力减小。这是由于流体动压效应受黏性剪切作用影响，滑移流效应宏观上等效于黏度的降低，黏度降低造成黏性剪切作用减弱，流体动压效应降低，开启力减小。从表3可以看出，随着压力的增大，滑移流效应减弱，低压时滑移流效应非常明显，而实际气体效应表现不明显，但随着压力增大实际气体效应增强。

5.3氢气密封性能计算及比较分析

5.3.1氢气第二维里系数计算在压力为0.1013 MPa，温度为300 K的条件下，由《Matheson气体数据手册》查得，氢气摩尔质量M=2.015 g·mol-1，临界温度Tc=33.18 K，临界压力pc=1.313 MPa，偏心因子e=-0.220，动力黏度m=0.902×10-5Pa·s。由式（5）可计算获得氢气的第二维里系数B=1.93179×10-5m3·mol-1。

5.3.2密封性能计算及比较分析选取外压po分别为低压0.202 MPa、中压4.5852 MPa、高压10 MPa进行计算分析，压力对氢气动力黏度影响忽略不计，选取不同气膜厚度计算氢气相关密封性能，计算结果绘制成曲线，如图4～图6所示。为准确表现相对误差，取气膜厚度为0.9 µm处相对误差绘制相对误差表格，如表4～表6所示。

图4及表4表明，低压工况下以氢气为密封介质时，滑移流效应影响误差达到18.3%，其误差增幅随气膜厚度的增大有增大的趋势，滑移流效应必须予以考虑。同一外压时，滑移流效应使泄漏率增大，实际气体效应使泄漏率减小。氢气实际气体效应对泄漏率的影响与氮气相反，这是由于氢气的第二维里系数B= 1.93179×10-5，即压缩因子Z＞1，这表明氢气实际气体比理想气体难于压缩，在相同压力的作用下，比理想气体具有更大的体积，宏观表现为标准状态下泄漏率Q降低。随着压力的增大，滑移流效应逐渐减弱，实际气体效应增强。氢气受滑移流效应影响的规律同氮气一致，但是，氢气受滑移流影响更加明显。

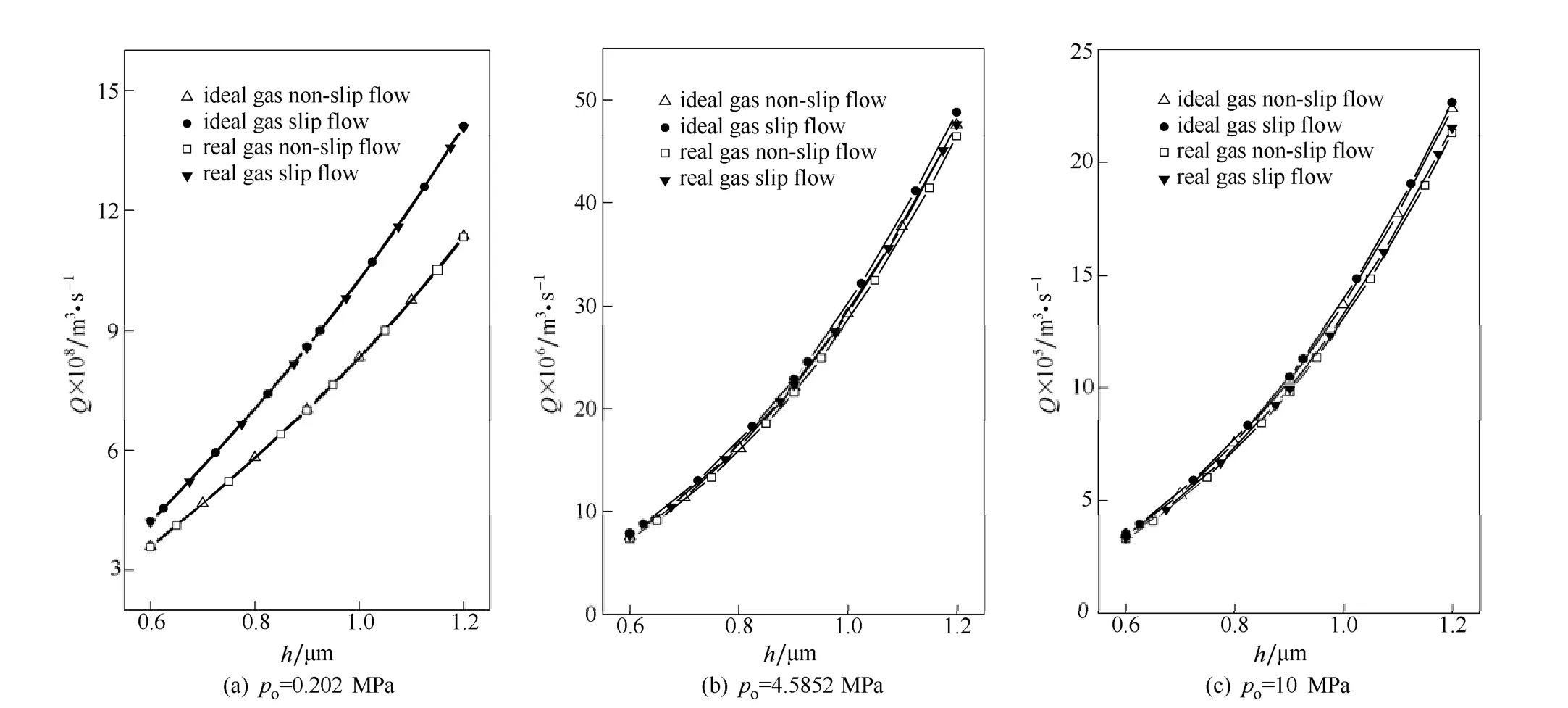
图4　氢气泄漏率Fig.4　Leakage for H2

图5　氢气槽根压力Fig.5　Pressure at spiral groove root radius for H2

图6　氢气开启力Fig.6　Opening force for H2

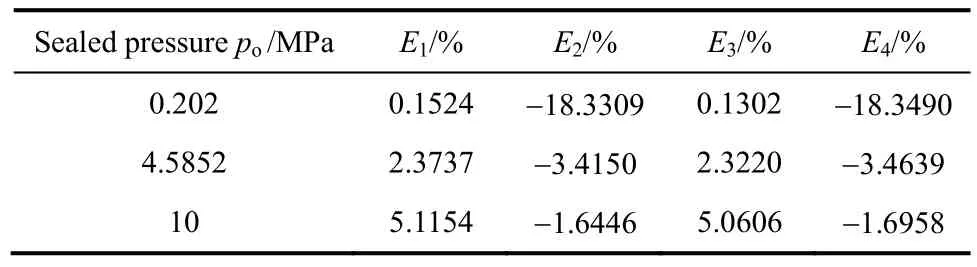
表4　氢气泄漏率相对误差Table 4　Error of leakage for H2

表5　氢气槽根压力相对误差Table 5　Error of pressure at groove root radius for H2

图5及表5表明，对于氢气，相同压力时实际气体效应和滑移流效应都使槽根处压力pg降低，随着压力增大，实际气体效应逐渐变得明显，滑移流效应急剧减弱，中压下4种情况的槽根处压力计算曲线接近，高压下槽根处压力规律与中压一致。

图6及表6表明，考虑实际气体效应时，氢气密封的端面开启力降低，这是由于氢气难于压缩，氢气实际气体槽根压力弱于理想气体，故产生的开启力减小。只考虑滑移流效应时，考虑滑移流影响的开启力低于不考虑滑移流的结果。

表6　氢气开启力相对误差Table 6　Error of opening force for H2

5.4二氧化碳密封性能计算及比较分析

5.4.1CO2第二维里系数计算在压力为0.1013 MPa，温度为300 K条件下，由《Matheson气体数据手册》查得，二氧化碳摩尔质量M=44.01 g·mol-1，临界温度Tc=304.19 K，临界压力pc=7.38 MPa，偏心因子e=0.228，动力黏度m=1.51× 10-5Pa·s。由式（5）可计算获得二氧化碳的第二维里系数B=-1.9172×10-4m3·mol-1。

5.4.2密封性能计算及比较分析选取外压po分别为低压0.202 MPa、中压4.5852 MPa进行计算分析。二氧化碳动力黏度高低压、中压下受压力影响并不明显，可忽略不计，然而，高压下，二氧化碳动力黏度不可视为恒定不变[20]，鉴于黏度与压力关系的复杂性，本文暂不对高压下二氧化碳作为密封气体的干气密封性能进行分析。二氧化碳相关密封性能计算结果如图7～图9所示。为准确表现相对误差，取气膜厚度为0.9 µm处相对误差绘制相对误差表格，如表7～表9所示。

图7表明，以二氧化碳为润滑气体的螺旋槽干气密封受实际气体效应影响规律与氮气相似，随着外压的增大实际气体效应影响急剧增大，滑移流效应影响减弱，这是由于二氧化碳的第二维里系数B=-1.19172×10-4m3·mol-1，即压缩因子小于1，实际气体容易受到压缩。表7显示，不同于氮气，二氧化碳在压力为0.202 MPa时，相对误差E1达到1.0699%，远大于氮气，这说明二氧化碳在低压时实际气体效应就已经很明显了。当压力达到中压4.5852 MPa时，相对误差E1迅速增大至15.149%，与氮气相比出现如此大的增幅是因为二氧化碳的压缩因子偏离理想气体更大，更容易被压缩的缘故。二氧化碳泄漏率受滑移流效应影响的规律同上述氮气、氢气时一致。

图8、表8表明，槽根处压力随气膜厚度增大而减小，低压工况下，实际气体与理想气体曲线近乎贴合，实际气体效应影响可以忽略，滑移流效应影响非常明显，同一压力下，滑移流效应使槽根处压力降低；中压工况下情况下相反，滑移流效应曲线与非滑移流效应曲线贴合，滑移流效应可以忽略，实际气体效应较显著，同一压力下实际气体效应使槽根处压力增大。说明低压下滑移流起主导作用，中压下实际气体效应起主导作用。

图7　二氧化碳泄漏率Fig.7　Leakage for CO2

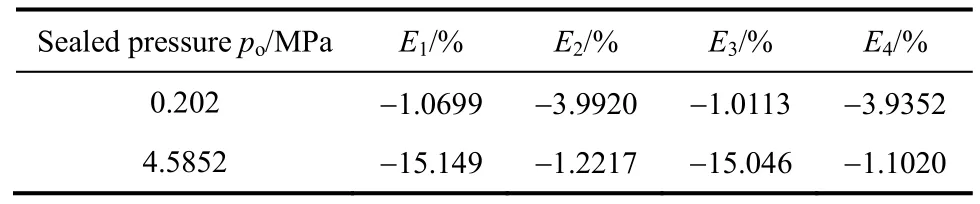
表7　二氧化碳泄漏率相对误差Table 7　Error of leakage for CO2

图9、表9表明，低压工况下，实际气体与理想气体曲线接近重合，滑移流效应使端面开启力减小，随着气膜厚度的增大，滑移流效应逐渐减弱，这是由于气膜厚度增大会导致Knudsen数变小。中压工况时，滑移流效应比较微弱，但此时不宜忽略，实际气体效应使端面开启力增大。

图8　二氧化碳槽根压力Fig.8　Pressure at spiral groove root radius for CO2

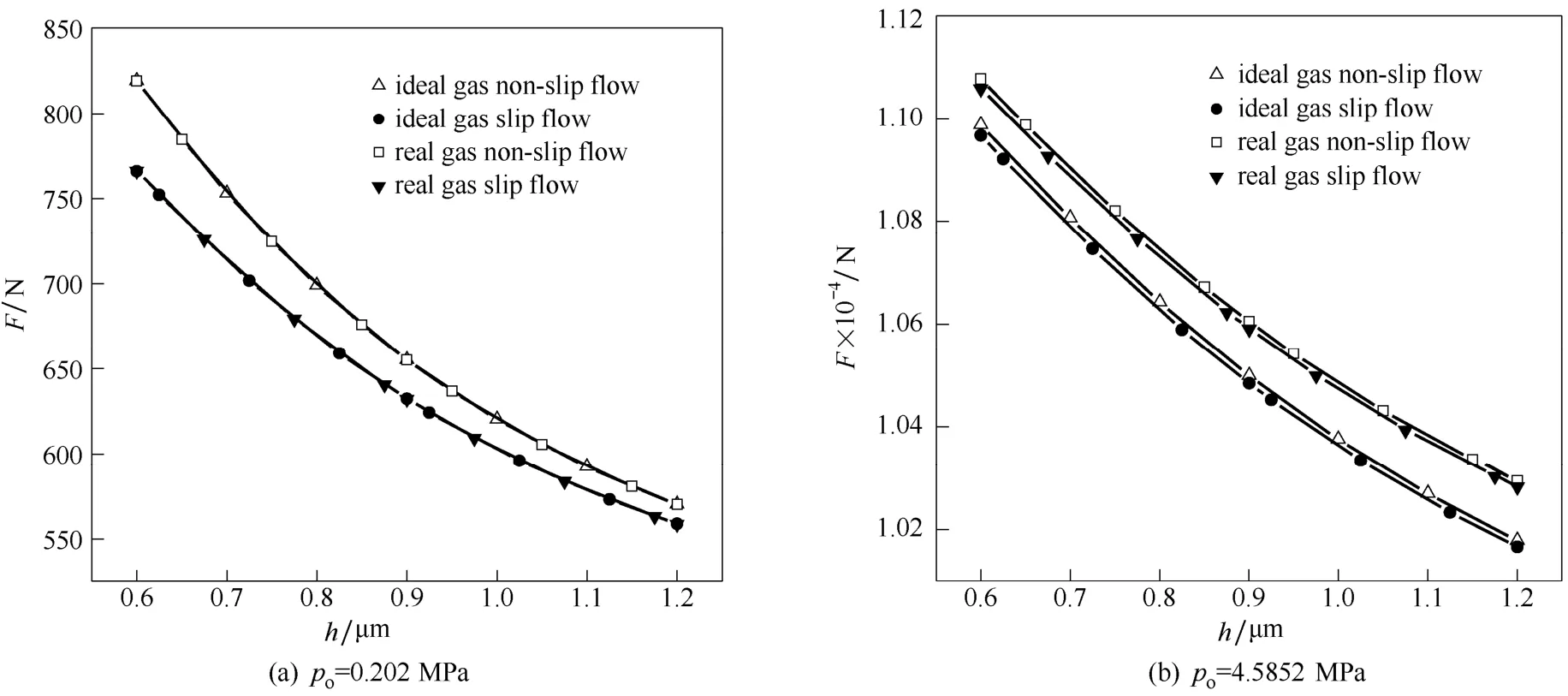
图9　二氧化碳开启力Fig.9　Opening force for CO2

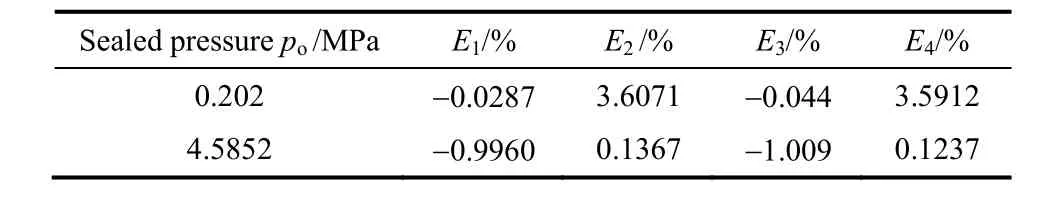
表9　二氧化碳开启力相对误差Table 9　Error of opening force for CO2

6　结　论

（1）基于螺旋槽的窄槽理论，提出了一种同时考虑滑移流效应和实际气体效应的螺旋槽干气密封性能分析的解析方法。用有效黏性系数表现滑移流效应、用维里实际气体状态方程表达实际气体效应。

（2）滑移流效应使气体泄漏率增大，槽根处压力和端面开启力降低；实际气体效应使易受压缩气体（压缩因子Z＜1）的泄漏率、槽根压力、端面开启力增大，例如氮气、二氧化碳等，而使不易受压缩气体（压缩因子Z＞1）的泄漏率、槽根压力、端面开启力减小，例如氢气等。

（3）低压工况下滑移流效应表现明显，实际气体效应微弱。随着压力增大，滑移流效应减弱，实际气体效应增强。低压下滑移流效应起主导作用，高压下实际气体效应起主导作用。较高外压工况下滑移流效应和实际气体效应均对螺旋槽干气密封性能有一定程度的影响，此时需要同时考虑两种效应。

符号说明

B ——第二维里系数，m3·mol-1

h，h0，h1——分别为两端面间非开槽区膜厚、端面开槽深度、开槽区膜厚，μm

μ——气体黏度，Pa·s

μeff——有效黏性系数，Pa·s

ρ——气体密度，kg·m-3

ω——密封环旋转角速度，rad·min-1

References

[1]温诗铸，黄平. 摩擦学原理 [M]. 第4版. 北京: 清华大学出版社，2012: 162-163. WEN S Z，HUANG P. Principles of Tribology [M]. 4th ed. Beijing: Tsinghua University Press，2012: 162-163.

[2]RUAN B. Finite element analysis of the spiral groove gas face at the low speed and the low pressure condition-slip flow consideration [J]. Tribology Transactions，2000，43 (3): 411-418. DOI: 1080/10402000008982357.

[3]丁雪兴，陈德林，张伟政，等. 螺旋槽干气密封微尺度流动场的近似计算及其参数优化 [J]. 应用力学学报，2007，24 (3): 425-428. DOI: 10.3969/j.issn.1000-4939.2007.03.020. DING X X，CHEN D L，ZHANG W Z，et al. An approximate calculation of the micro-scale effect flow field of a spiral groove dry gas seal and parameter optimization [J]. Chinese Journal of Applied Mechanics，2007，24 (3): 425-428. DOI: 10.3969/j.issn.1000-4939.2007.03.020.

[4]丁雪兴，王悦，张伟政，等. 螺旋槽干气密封润滑气膜角向涡动的稳定性分析 [J]. 北京化工大学学报 (自然科学版)，2008，35 (2): 82-86. DOI: 10.3969/j.issn.1671-4628.2008.02.019. DING X X，WANG Y，ZHANG W Z，et al. A stability analysis for lubricating gaseous film of spiral grooved gas seals subjected to angular eddy motion [J]. Journal of Beijing University of Chemical Technology (Natural Science Edition)，2008，35 (2): 82-86. DOI: 10.3969/j.issn.1671-4628.2008.02.019.

[5]尹晓妮. 中低转速螺旋槽干式气体端面密封的数值分析 [D]. 东营: 中国石油大学(华东)，2006. YIN X N. Numerical analyses of spiral-grooved dry gas face seals at low and moderate speeds [D]. Dongying: China University of petroleum (East of China)，2006.

[6]许静，彭旭东，白少先，等. 气体热黏效应对干气密封性能影响的数值分析 [J]. 上海交通大学学报，2012，46 (5): 722-728. XU J，PENG X D，BAI S X，et al. Numerical analysis of gas thermal viscosity effect on performance of a spiral-groove gas face seal [J]. Journal of Shanghai Jiaotong University，2012，46 (5): 722-728.

[7]许静，彭旭东，白少先，等. 端面微尺度效应和热黏效应对干气密封性能的影响 [J]. 化工学报，2013，64 (9): 3291-3300. DOI: 10.3969/j.issn.0438-1157.2013.09.030. XU J，PENG X D，BAI S X，et al. Effects of surface micro-scale and thermal viscosity on sealing performance of spiral-grooved dry gas seal [J]. CIESC Journal，2013，64 (9): 3291-3300. DOI: 10.3969/j.issn.0438-1157.2013.09.030.

[8]蒋小文，顾伯勤. 螺旋槽干气密封端面间气膜特性 [J]. 化工学报，2005，56 (8): 1419-1425. JIANG X W，GU B Q. Characteristic of gas film between spiral groove dry gas seal faces [J]. Journal of Chemical Industry and Engineering (China)，2005，56 (8): 1419-1425.

[9]彭旭东，江锦波，白少先，等. 中低压干气密封螺旋槽结构参数优化 [J]. 化工学报，2014，65 (11): 4536-4542. DOI: 10.3969/j.issn.0438-1157.2014.11.046. PENG X D，JIANG J B，BAI S X，et al. Structural parameter

F ——开启力，N

Kn ——Knudsen数

k ——Boltzmann常数

M ——气体摩尔质量，g·mol-1

m ——单个分子质量，kg

Na——阿伏伽德罗常数

p，p，p，p ——分别为两端面间任意处的压力、螺旋槽

gio

槽根处压力、密封环内径处压力、外径处压力，MPa

pc——临界压力，MPa

Q ——泄漏率， m3·s-1

R ——气体常数，J·(mol·K)-1

r ——密封环端面任意处的半径，mm

ri，ro——分别为密封环内径、外径，mm

rg——密封环端面螺旋槽槽根处半径，mm

St——气体通过密封面的质量流量，kg·s-1

T，Tc——分别为气体热力学温度和临界温度，K

Tr——对比温度，Tr=T/Tc

u ——数值因子

v ——摩尔体积，mol·L-1

Z ——压缩因子

α ——螺旋角

γ ——台宽与槽宽之比

ε ——偏心因子

λ ——分子平均自由程，moptimization of spiral groove dry gas seal under low or medium pressure [J]. CIESC Journal，2014，65 (11): 4536-4542. DOI: 10.3969/j.issn.0438-1157.2014.11.046.

[10]宋鹏云，张帅. 滑移流影响螺旋槽干气密封性能的解析法 [J]. 排灌机械工程学报，2014，32 (10): 877-882. DOI: 10.3969/j.issn.1674-8530.14.002. SONG P Y，ZHANG S. An approximate analytical method of characteristics of spiral groove dry gas seals under slip flow conditions [J]. Journal of Drainage and Irrigation Machinery Engineering，2014，32 (10): 877-882. DOI: 10.3969/j.issn.1674-8530.14.002.

[11]孟光，张文明. 微电系统动力学 [M]. 北京: 科学出版社，2008.151-152. MENG G，ZHANG W M. Micro-Electro-Mechanical System Dynamics [M]. Beijing: Science Press，2008. 151-152.

[12]施云海，王艳莉，彭阳峰，等. 化工热力学 [M]. 上海: 华东理工大学出版社，2007: 19. SHI Y H，WANG Y L，PENG Y F，et al. Chemical Engineering Thermodynamics [M]. Shanghai: East China University of Science and Technology Press，2007: 19.

[13]宋鹏云，胡晓鹏，许恒杰. 实际气体对T槽干气密封动态特性的影响 [J]. 化工学报，2014，65 (4): 1344-1352. DOI: 10.3969/j.issn.0438-1157.2014.04.026. SONG P Y，HU X P，XU H J. Effect of real gas on dynamic performance of T-groove dry gas seal [J]. CIESC Journal，2014，65 (4): 1344-1352. DOI: 10.3969/j.issn.0438-1157.2014.04.026.

[14]ALESSANDRO V. A simple modification of the pitzer method to predict second virial coefficients [J]. The Canadian Journal of Chemical Engineering，2007，85 (1): 118-121. DOI: 10.1002/cjce.5450850112.

[15]CHAPMAN S，COWLING T G. The Mathematical Theory of Non-uniform Gases: an Account of the Kinetic Theory of Viscosity，Thermal Conduction and Diffusion in Gases [M]. 3rd ed. Cambridge: Cambridge University Press，1970: 89-99.

[16]LEVINE I N. Physical Chemistry [M]. 6th ed. New York: McGraw-Hill，2009: 458.

[17]JENNINGS S G. The mean free path in air [J]. Journal of Aerosol Science，1988，19 (2): 159-166. DOI: 10.1016/0021-8502(88)90219-4.

[18]MUIJDERMAN E A. Spiral Groove Bearings [M]. BATHGATE R H trans. New York: Springer-Verlag，1966: 17-21.

[19] 卡尔L 约思. Matheson气体数据手册 [M]. 陶鹏万，黄建彬，朱大方，译. 第7版. 北京: 化学工业出版社，2003: 432-436. CARL Y. Matheson Gas Data Book [M]. TAO P W，HUANG J B，ZHU D F，trans. 7th ed. Beijing: Chemical Industry Press，2003: 432-436.

[20]张家荣，赵廷元. 工程常用物质的热物理性质手册 [M]. 北京: 新时代出版社，1987: 273. ZHANG J R，ZHAO T Y. Handbook of Thermophysical Properties for Commonly Used Engineering Materials [M]. Beijing: New Time Press，1987: 273.

Analysis of performance of spiral groove dry gas seal considered effects of both real gas and slip flow

SONG Pengyun，ZHANG Shuai，XU Hengjie
(Faculty of Chemical Engineering，Kunming University of Science and Technology，Kunming 650500，Yunnan，China)

Abstract:In order to analyze the performance of the spiral groove dry gas seal considered effects of both real gas and slip flow simultaneously，the modified pressure governing equations of the seal based on the narrow groove theory by taking the effective viscosity coefficient instead of the gas dynamic viscosity and the real gas Virial state equation instead of the ideal gas state equation. N2，H2，CO2were taken as examples. The leakage，the pressure at groove root radius and the opening force of the seal were calculated. Meanwhile，the leakage，the pressure at groove root radius and the opening force under the condition of ideal gas without slip flow，ideal gas with slip flow，real gas without slip flow and real gas with slip flow were compared，respectively. The results showed that the effect of slip flow made the leakage increase，and the pressure at groove root radius and the opening force decrease. The effect of real gas made the leakage，the pressure at groove root radius and opening force of susceptible compressed gas (Z＜1) increase whereas the leakage，the pressure at groove root and opening force of non-susceptible compressed gas (Z＞1) decrease. With increasing sealed pressure po，the effect of slip flow was reduced，while that of the real gas was strengthened. Under the condition of low sealed pressure，the slip flow effect was significant. On the contrary，the real gas effect played a predominant role under the condition of high sealed pressure.

Key words:dry gas seal; spiral groove; slip flow; real gas; spiral narrow groove theory; carbon dioxide

DOI：10.11949/j.issn.0438-1157.20151358

中图分类号：S 277.9；TH 136

文献标志码：A

文章编号：0438—1157（2016）04—1405—11

基金项目：国家自然科学基金项目（51465026）。

Corresponding author:Prof. SONG Pengyun，songpengyunkm@sina.com