环丁烯砜合成反应的基团贡献法热力学分析

王修纲，沈阳，田冰虎，吴凤超，吴剑华，（天津大学化工学院，天津 30007；沈阳化工大学化学工程学院，辽宁 沈阳 04）



环丁烯砜合成反应的基团贡献法热力学分析

王修纲1，沈阳2，田冰虎2，吴凤超2，吴剑华1，2
（1天津大学化工学院，天津 300072；2沈阳化工大学化学工程学院，辽宁 沈阳 110142）

摘要：采用基团贡献法对环丁烯砜合成反应进行了热力学分析，计算了300～600 K、0.1～10 MPa反应体系的反应焓变、反应熵变、反应Gibbs自由能变和反应平衡常数，并分析了温度、压力和组成对平衡转化率的影响。结果表明，标准压力下，环丁烯砜合成反应是可逆放热反应，温度小于460 K范围内可以自发进行，降低温度和升高压力有利于反应向正向进行。温度、压力和组成对平衡转化率均有影响，温度影响最为显著。降低温度、升高压力或增大过量比有利于提高平衡转化率，最大平衡转化率接近于1。基团贡献法所得的平衡转化率预测值与实验值吻合较好，相对偏差在10%以内。

关键词：环丁烯砜；基团贡献法；热力学；环丁砜

2015-08-13收到初稿，2015-09-23收到修改稿。

联系人：吴剑华。第一作者：王修纲（1986—），男，博士研究生。

Received date: 2015-08-13.

Foundation item: supported by the National Natural Science Foundation of China(51406125).

引　言

环丁烯砜是合成环丁砜的必要中间体。环丁砜是一种重要的有机溶剂，因其具有热稳定性好、溶解能力强、选择性高、设备腐蚀性弱、易回收、毒性小等优点，使其广泛应用于芳烃抽提、气体净化以及作为反应溶剂等领域[1-3]。

环丁烯砜是由1,3-丁二烯和二氧化硫在阻聚剂的存在下进行Diels-Alder反应制取的。将环丁烯砜脱除过量二氧化硫后催化加氢可获得环丁砜，这是环丁砜工业化合成的唯一路线。国内外对环丁砜的生产工艺、催化剂和应用等已有大量报道[4-6]。然而，由于环丁烯砜热力学数据的缺乏，限制了环丁烯砜合成反应的热力学分析。Mackle等[7]通过计算仅得到了环丁烯砜合成反应是放热反应的结论，未进行深入的热力学分析。关于环丁烯砜合成体系热力学分析的研究鲜有报道。

物质热力学数据的估算方法主要有基团贡献法[8-10]、绝热量热法[11-12]和分子模拟法[13-14]等。本文将采用Benson和Joback基团贡献法对反应体系中各物质缺失的热力学数据进行估算，进而计算不同温度和压力下的反应焓变、Gibbs自由能变和反应平衡常数，并将平衡常数与平衡转化率建立联系，考察温度、压力和组成对环丁烯砜合成反应平衡转化率的影响。进而为该体系反应条件的优化和应用提供理论依据。

1　反应体系热力学数据的计算

环丁烯砜是由1,3-丁二烯与二氧化硫发生Diels-Alder反应生成，其反应方程式如下[4]

表1　环丁烯砜及1,3-丁二烯的热力学基团贡献值（Benson法）Table 1　Thermodynamic data of group contribution of sulfolene and 1,3-butadiene (Benson method)

表2　气相条件下各物质的ΔfH⊝298K、S⊝298K以及不同温度下的c⊝pTable 2　ΔfH⊝298K，S⊝298Kand c⊝pat different temperature in gas phase

反应体系中，1,3-丁二烯与二氧化硫的热力学数据可由文献[15-19]获得，而环丁烯砜热力学数据尚缺失，本文采用基团贡献法进行估算。

1.1气态条件下环丁烯砜热力学数据的估算

Benson基团贡献法具有较高的精度，且适用范围较广，普遍用于估算标准生成焓和标准熵[20]。Benson基团贡献法的计算公式为

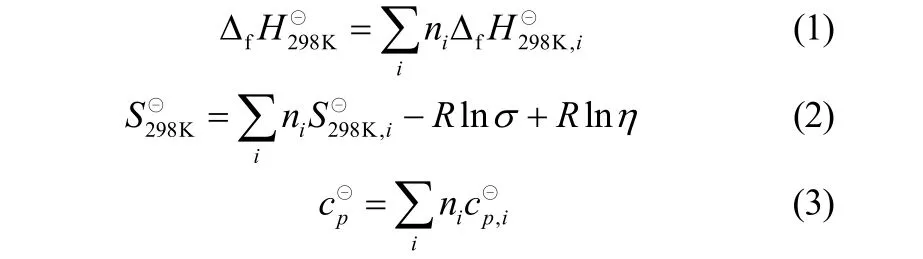
式中，i代表i型基团，也代表本法所规定的修正项；ni是i基团的数目；ΔfH⊝298K,i、S⊝298K,i、c⊝p,i各为相应的i基团的基团参数；σ为总对称数，η为光学异构体数。基团贡献值[21]如表1所示。

经过计算和文献[15]得到气态条件下各物质在298 K时的ΔfH⊝298K和S⊝298K以及不同温度下的c⊝p，列于表2。

1.2环丁烯砜临界温度、临界压力和偏心因子的估算

Joback基团贡献法是按官能团划分基团的，对于相同基团参照该基团所在分子的主体结构及特点进行进一步细分，提高了计算精度[22]。其所用的估算公式为

式中，Tc为临界温度，K；pc为临界压力，bar(1bar=100 kPa)；Tb是正常沸点，K；ΔTci、Δpci分别为基团对临界性质的贡献值，nA是分子中的原子数。各基团的ΔTci、Δpci值列于表3[22]。

表3　环丁烯砜及1,3-丁二烯的热力学基团贡献值（Joback法）Table 3　Thermodynamic data of group contribution of sulfolene and 1,3-butadiene (Joback method)

再通过Edmister方程即可求得偏心因子ω，其计算公式如下

式中，pc的单位是atm（1atm=101.325 kPa）。

通过计算，各物质的Tc、pc和ω值列于表4。

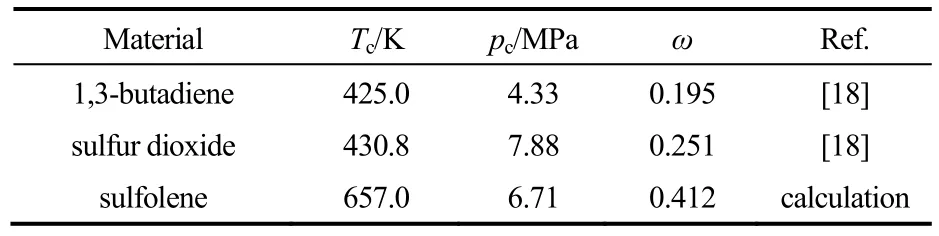
表4　反应体系中各物质的Tc、pc和ω值Table 4　Tc，pcand ω values

Benson法和Joback法计算1,3-丁二烯的各项热力学数据与文献相比较，结果如表5所示。计算结果与文献值的最小相对偏差为0.02%，最大相对偏差为0.91%，说明Benson和Joback基团贡献法得到的环丁烯砜的基础热力学数据是可靠的，可用于下述的热力学计算及分析。

1.3液态条件下各物质热力学数据的估算

通过Riedle方程[式（8）]可以求出环丁烯砜标准沸点下的汽化焓，再通过Watson方程[式（9）]即可算出298 K时各物质的汽化焓。

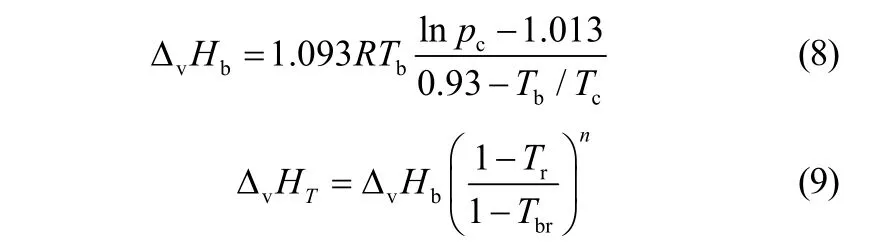
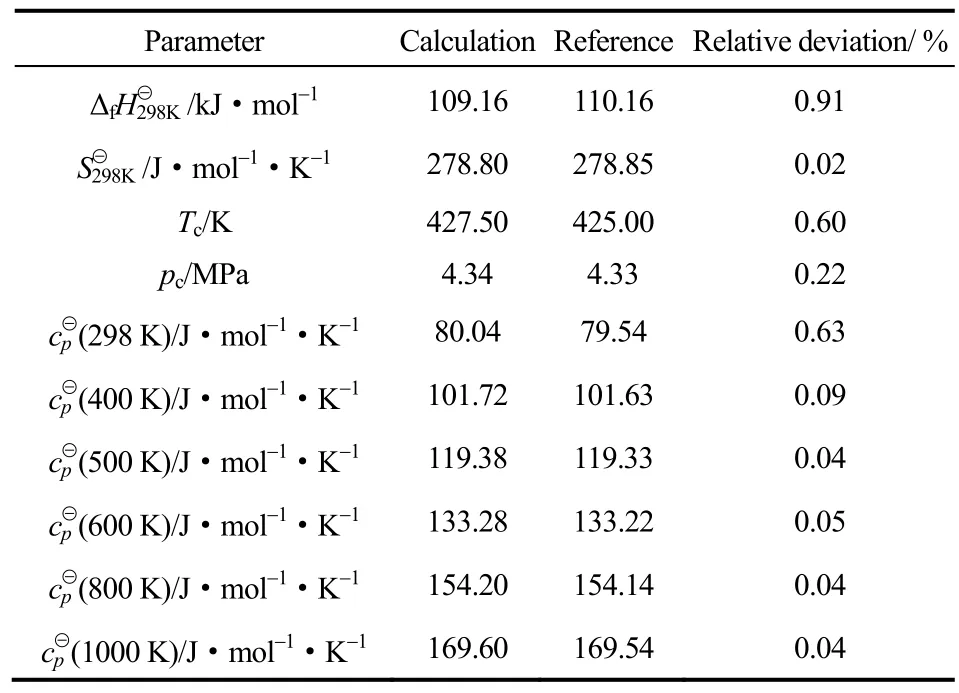
表5　1,3-丁二烯热力学数据计算值与文献值的比较Table 5　Comparison of calculation data and document data of 1,3-butadiene

各物质在标准沸点下的汽化熵由式（10）求得，再通过设计相态循环即可算出298 K时各物质的汽化熵。

再根据式（11）和式（12）即可算出298 K时各物质液相的标准摩尔生成焓和标准熵，其值列于表6。

通过Rowlison-Bondi方程可以计算不同温度下液相环丁烯砜的摩尔热容，液相1,3-丁二烯和二氧化硫的摩尔热容通过文献[16]和文献[17]查得。

再利用Origin软件进行多项式回归得到cpl与T的多项式回归方程如表6所示。

表6　液相条件下各物质的ΔfH⊝298K、S⊝298K以及c⊝p与温度关系的多项式回归方程Table 6　ΔfH⊝298K，S⊝298Kand polynomial equation of c⊝pwith temperature in liquid phase

1.4标准反应焓变、熵变、Gibbs自由能变和平衡常数

通过以上求得的热力学数据，根据热力学公式计算不同温度下标准反应焓变、标准反应熵变、标准反应Gibbs自由能变和标准平衡常数，数值列于表7。

表7　不同温度下反应的ΔrH⊝、ΔrS⊝、ΔrG⊝和lnK⊝Table 7　ΔrH⊝，ΔrS⊝，ΔrG⊝and lnK⊝of reaction at different temperature

2　反应体系热力学分析与讨论

2.1温度对标准反应焓变、Gibbs自由能变和平衡

常数的影响

由表7可以看出标准反应焓变、标准反应Gibbs自由能变和标准平衡常数随温度的变化趋势。环丁烯砜合成反应在300～600 K范围内标准反应焓变均小于零，说明反应为放热反应；随着反应温度的升高，标准反应焓变呈减小趋势，说明随反应温度的升高，反应的放热量增大。反应的标准Gibbs自由能变在温度小于460 K的范围内均小于零，说明在该温度范围内反应自发进行；随着反应温度的升高，Gibbs自由能变增大，说明升高温度不利于该反应向正向进行。反应平衡常数随温度升高而减小，说明反应平衡转化率随温度升高而减小。

2.2压力对反应Gibbs自由能变和平衡常数的

影响

根据热力学第一定律及热力学第二定律推得的基本公式dG=Vdp-SdT进行反应Gibbs自由能变的分析，等温条件下进行积分，并代入ΔrG⊝ (T)，得恒温下ΔrG随压力变化的关系式

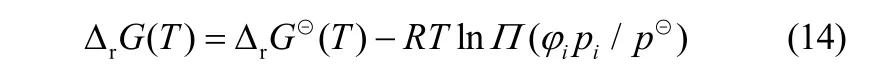
式中，φ表示逸度系数，由高压下预测精度较高的RK方程计算。由于反应需要在较高的温度和压力下进行，利用式（13）、式（14）计算了2、4、6、8和10 MPa下反应的Gibbs自由能变及平衡常数随温度的变化趋势。本文热力学分析的温度和压力范围已覆盖了文献报道和实际生产的反应条件。不同压力下反应的Gibbs自由能变及平衡常数随温度的变化曲线如图1所示。

由图1（a）可以看出ΔrG随压力升高而减小，说明升高压力有利于反应向正向进行。对不同压力，在一定的温度范围内均有ΔrG小于零，说明反应在0.1～10 MPa内均可自发进行。由图1（b）可以看出平衡常数随压力的升高而增大，说明反应平衡转化率随压力升高而增大。

图1　不同压力下反应Gibbs自由能变、平衡常数与温度的关系Fig.1 ΔrG and lnK of reaction at different pressure as a function of temperature

2.3平衡转化率的预测

在实际反应中，平衡转化率是环丁烯砜合成反应的重要指标。将平衡常数与平衡转化率建立关系，获得反应物的平衡转化率可为实际反应体系分析提供参考。

平衡常数与平衡时反应体系中物质浓度之间的关系见式（15）。

式中，yeqB(g)、xeqB(l)分别为体系平衡时气相B和液相B的摩尔分数，p为反应压力，p⊝为标准压力，νB为组分B的化学计量数，φ为逸度系数，γ为活度系数。由于考察范围内1,3-丁二烯和二氧化硫均处于超临界状态或亚临界状态，为简化计算，此处忽略气相反应并将活度系数近似为1去估算平衡转化率，则式（15）简化为式（16）。由式（16）及化学反应方程式可得不同温度、压力及组成下平衡转化率。

本文平衡转化率（α）是以1,3-丁二烯为关键组分定义的。采用过量比（δ）表示反应物组成，定义过量比为二氧化硫与1,3-丁二烯的摩尔比，此处仅讨论二氧化硫过量的情况，即δ≥1。图2为过量比为1.2时，温度与压力变化对平衡转化率的影响；图3为压力为4 MPa时，温度和组成对平衡转化率的影响。

由图2、图3可以看出，温度、压力和组成对平衡转化率均有影响。温度对平衡转化率的影响最为显著，在大部分压力及过量比范围内，温度低于400 K时，平衡转化率接近于1；温度高于520 K时，平衡转化率接近于0；温度在420～480 K之间平衡转化率的变化率较大。压力对平衡转化率的影响较为显著，平衡转化率随压力升高而增大，当压力高于4 MPa时，平衡转化率增大趋势变缓。组成对平衡转化率有一定影响，当过量比接近于1时，平衡转化率减小；δ>1.8时，过量比对平衡转化率的影响减弱。对于1,3-丁二烯过量的情况也进行了计算，其影响关系与二氧化硫过量一致。需要说明的是，由于真实反应中各组分活度系数均小于1，由式（15）可知活度系数取1会使平衡转化率预测值偏低，但图2、图3所示的平衡转化率随各条件的变化趋势仍是有效的。

图2　温度和压力对平衡转化率的影响Fig.2　Effect of temperature and pressure on equilibrium conversion

图3　温度和组成对平衡转化率的影响Fig.3　Effect of temperature and composition on equilibriumconversion

表8　平衡转化率的实验值和预测值对比Table 8　Data comparison of experiment and calculations

为了验证平衡转化率预测值的准确性，本文将平衡转化率预测值与实验值进行对比，结果见表8。从表中可以看出实验值与预测值比较吻合，相对偏差（以实验值为基准）在10%以内，且数值的变化趋势一致，表明平衡转化率的预测值相对可靠。此外，在较低的反应温度下，受动力学因素影响，反应达平衡所需的时间变长，导致在一定反应时间下，低温条件（400 K以下）所得的平衡转化率实验值偏低，相对偏差较大。

3　结　论

通过基团贡献法计算了环丁烯砜合成反应体系中各物质的基础热力学数据，进而获得反应的标准反应焓变、标准反应Gibbs自由能变及标准平衡常数。分析了温度和压力对反应Gibbs自由能变、平衡常数的影响以及温度、压力和组成对平衡转化率的影响。结果表明：

（1）标准压力下，300～600 K温度范围内环丁烯砜合成反应是可逆放热反应，反应Gibbs自由能在温度小于460 K的范围内均小于零，在此温度范围内为自发过程，且平衡常数为1.15～4.30×106，反应在热力学上完全可行。

（2）平衡常数和Gibbs自由能变受温度、压力影响，降低温度或升高压力，反应Gibbs自由能变减小、平衡常数增大，有利于反应向正向进行。

（3）温度、压力和组成对平衡转化率均有影响，温度影响最为显著。降低温度、升高压力或增大过量比有利于提高平衡转化率，最大平衡转化率接近于1。

（4）基团贡献法所得的平衡转化率预测值与实验值吻合较好，相对偏差在10%以内。

符号说明

cp——比定压热容，J·mol-1·K-1

ΔG ——Gibbs自由能变，kJ·mol-1

ΔH ——焓变，kJ·mol-1

K ——化学平衡常数

p ——压力，MPa

R ——摩尔气体常数，J·mol-1·K-1

ΔS ——熵变，J·mol-1·K-1

T ——温度，K

x ——液相的摩尔分数

y ——气相的摩尔分数

α ——平衡转化率

δ

——过量系数

η ——分子光学异构体数

ν ——化学计量数

σ ——分子对称数

φ ——逸度系数

ω ——偏心因子

上角标

eq ——平衡状态

⊝——标准态

下角标

b——常压沸点

c——临界点

f——生成态

g——气态

i——基团数

l——液态

r——反应态

v——蒸发态

References

[1] ULF T. Sulfolane: a versatile dipolar aprotic solvent [J]. Organic Process Research & Development，2012，16(7): 1273-1278.

[2] ZHANG Q，CHEN J J，WANG X Y，et al. Enhanced electrochemical performance and thermal stability of LiNi0.5Mn1.5O4using an electrolyte with sulfolane [J]. Physical Chemistry Chemical Physics，2015，17(16): 10353-10357.

[3] ZARETSKII M I，RUSAK V V，CHARTOV E M. Sulfolane in liquid extraction: a review [J]. Coke and Chemistry，2011，54(6): 211-214.

[4] CLARK E. Kirk-Othmer Encyclopedia of Chemical Technology[M]. New York: John Wiley & Sons，Inc.，2000.

[5] BANDO S，KANDA H，ONODA Y，et al. Method for manufacturing sulfolene compound and method for manufacturing sulfolane compound: US8436193[P]. 2013.

[6] MA Y F，Li W，ZHANG M H，et al. Preparation and catalytic properties of amorphous alloys in hydrogenation of sulfolene [J]. Applied Catalysis A: General，2003，243(2): 215-223.

[7] MACKLE H，MCNALLY D V. Studies in the thermochemistry of sulphones(9): Thermochemistry of the butadiene and isoprene sulphones [J]. Transactions of the Faraday Society，1969，65: 1738-1741.

[8] SADIYE V，TANTEKIN S B. Prediction of gas permeability coefficients of copolyimides by group contribution methods [J]. Journal of Membrane Science，2015，480: 47-63.

[9] VALDERRAMA J O，FORERO L A，ROJAS R E. Extension of a group contribution method to estimate the critical properties of ionic liquids of high molecular mass [J]. Industrial & Engineering Chemistry Research，2015，54(13): 3480-3487.

[10] TABERNERO A，VALLE E M，GALÁN M A. Estimation of sublimation enthalpies of solids constituted by aromatic and/or polycyclic aliphatic rings by using a group contribution method [J]. AIChE Journal，2012，58(9): 2875-2884.

[11] WANG L，TAN Z C，MENG S H，et al. Enhancement of molar heat capacity of nanostructured Al2O3[J]. Journal of Nanoparticle Research，2001，(3): 483-487.

[12] 徐抗震，宋纪蓉，赵凤起，等. 1,1-二氨基-2,2-二硝基乙烯的比热容、热力学性质及绝热至爆时间研究 [J]. 化学学报，2007，65(24): 2827-2831. XU K Z，SONG Q R，ZHAO F Q，et al. Special heat capacity，thermodynamic properties and adiabatic time-to-explosion of 1,1-diamino-2,2-dinitroethylene [J]. Acta Chimica Sinica，2007，65(24): 2827-2831.

[13] 吕乐，杨座国，赵颖. 4-硝基苯胂酸合成反应的热力学计算机模拟[J]. 化工学报，2014，65(9): 3317-3322. DOI: 10.3969/j.issn. 0438-1157.2014.09.002. LÜ L，YANG Z G，ZHAO Y. Thermodynamics computational simulation of 4-nitrophenylarsonic acid synthesis [J]. CIESC Journal，2014，65(9): 3317-3322. DOI: 10.3969/j.issn.0438-1157.2014.09.002.

[14] QI W，RICARDO G C，NORA H D. Mixing thermodynamics of the calcite-structured (Mn,Ca)CO3solid solution: a computer simulation study [J]. The Journal of Physical Chemistry B，2011，115(47): 13854-13861.

[15] 傅献彩，沈文霞，姚天扬，等. 物理化学[M]. 北京: 高等教育出版社，2005: 483-495. FU X C，SHEN W X，YAO T Y，et al. Physics Chemistry[M]. Beijing: Higher Education Press，2005: 483-495.

[16] 刘光启，马连湘，刘杰. 化学化工物性数据手册（有机卷）[M]. 北京: 化学工业出版社，2002: 123 LIU Q G，MA L X，LIU J. Handbook of Chemistry and Chemical Properties Data (Organic Volume) [M]. Beijing: Chemical Industry Press，2002: 242.

[17] 刘光启，马连湘，刘杰. 化学化工物性数据手册（无机卷）[M]. 北京: 化学工业出版社，2002: 123. LIU Q G，MA L X，LIU J. Handbook of Chemical and Chemical Physical Data (Inorganic Volume) [M]. Beijing: Chemical Industry Press，2002: 123.

[18] 朱自强，吴有庭. 化工热力学[M]. 北京: 化学工业出版社，2009: 332-333. ZHU Z Q，WU Y T. Chemical Thermodynamics [M]. Beijing: Chemical Industry Press，2009: 332-333.

[19] DEAN J A. Lange’s Handbook of Chemistry[M]. 15th ed. New York: McGraw-Hill，1999: Section 6: 53，139.

[20] 王琳琳，陈建云，梁杰珍，等. 枞酸与甲醇酯化反应的基团贡献法热力学分析[J]. 化工学报，2013，64(6): 1900-1906. DOI: 10.3969/j.issn.0438-1157.2013.06.002. WANG L L，CHEN J Y，LIANG J Z，et al. Thermodynamic analysis for esterfication of abietic acid with methanol by group-contribution method [J]. CIESC Journal，2013，64(6): 1900-1906. DOI: 10.3969/j.issn. 0438-1157. 2013.06.002.

[21] POLING B E. 气液物性估算手册[M]. 赵红玲，译. 5版. 北京: 化学工业出版社，2006: 48-64. POLING B E. The Properties of Gases and Liquids[M]. ZHAO H L，trans. 5th ed. Beijing: Chemical Industry Press，2006: 48-64.

[22] 董新法，方利国，陈砺. 物性估算原理及计算机计算[M]. 北京: 北京工业出版社，2006: 151-153. DONG X F，FANG L G，CHEN L. Physical Property Estimation Principle and Computer Calculation[M]. Beijing: Chemical Industry Press，2006: 151-153.

Thermodynamic analysis on synthesis of sulfolene by group-contribution method

WANG Xiugang1，SHEN Yang2，TIAN Binghu2，WU Fengchao2，WU Jianhua1,2
(1School of Chemical Engineering and Technology，Tianjin University，Tianjin 300072，China;2School of Chemical Engineering，Shenyang University of Chemical Technology，Shenyang 110142，Liaoning，China)

Abstract:The thermodynamic analysis of sulfolene synthesis reaction was carried out by group-contribution method. The reaction enthalpy，entropy，Gibbs free energy and equilibrium constant were calculated in the temperature range of 300—600 K and the pressure range of 0.1—10 MPa. The effects of temperature，pressure and reactant ratio on equilibrium conversion were also discussed. The calculation results indicate that sulfolene synthesis is a reversible exothermic reaction，and it is spontaneous when the temperature is less than 460 K at standard pressure. The reaction occurs more easily at lower temperatures and higher pressures. Temperature，pressure and the reactants ratio all show significant effect on equilibrium conversion，and the temperature is the most significant factor. Lower temperature，higher pressure and higher reactant ratio favor the promotion of equilibrium conversion，and the maximum equilibrium conversion is close to 1. The experimental results show good agreement with the thermodynamic calculation，and the relative deviation is less than 10%.

Key words:sulfolene; group contribution; thermodynamic; sulfolane

DOI：10.11949/j.issn.0438-1157.20151302

中图分类号：TQ 031.1

文献标志码：A

文章编号：0438—1157（2016）04—1103—07

基金项目：国家自然科学基金项目(51406125)。

Corresponding author:Prof. WU Jianhua，jianhuawu@163.com