算数亚式期权价格敏感性参数估计方法研究

王维国，张博翔

(东北财经大学经济学院，辽宁大连　116025)

算数亚式期权价格敏感性参数估计方法研究

王维国，张博翔

(东北财经大学经济学院，辽宁大连116025)

摘要：结合几何亚式期权敏感性参数的估计，引入控制变量，推导出算数亚式期权价格敏感性参数估计方法，在此基础上，对蒙特卡罗模拟的控制变量法和传统的CRN法进行对比分析，结果发现控制变量法不但改进了估计精度及模拟效率，而且能更好地进行误差控制。

关键词:亚式期权；敏感性参数；控制变量

一、引言

亚式期权(Asian option)是一种重要的奇异期权(exotic option)，与一般欧式期权不同，亚式期权的到期收益取决于某一段时间的平均价格(几何平均价格或算术平均价格)，而非标的资产到期日的价格。与欧式期权类似，影响亚式期权价格的主要因素包括标的资产价格、无风险利率、到期时间等。亚氏期权价格的敏感性参数(Greeks)是指当其中某一因素发生变化时，引起亚氏期权价格变化的情况(大小和方向)。敏感性参数是金融机构和投资者利用期权进行投资管理、风险控制的重要参考指标，因此采用适当的方法提高亚氏期权价格的敏感性参数估计精度具有重要的现实意义。

亚式期权可分为几何平均亚式期权与算术平均亚式期权两类，由于服从对数正态分布的标的资产价格的几何平均值依然服从对数正态分布，因此在Black-Scholes模型假设下几何亚式期权的敏感性参数可以通过类似欧式期权定价的方法获得解析解。然而，市场上算术平均亚式期权较几何平均亚式期权更为常见，但是由于无法获得价格算术平均值的分布函数，算术亚式期权的价格敏感性参数只能通过各类数值方法进行近似估计。本文将利用几何亚式期权的敏感性参数的解析解，构建控制变量，探寻算术亚式期权敏感性参数的最优估计方法。

二、文献评述

Monte Carlo模拟是亚式期权敏感度分析的常用方法[1]，但如果将传统的Monte Carlo模拟直接应用于亚式期权敏感度分析，尤其是算术平均亚式期权，会存在两个重要的缺陷：首先，Monte Carlo模拟给出的估计值不能保证是无偏的；其次，运用Monte Carlo方法进行反复模拟，运算量巨大。鉴于此，国外研究者提出了以无穷小扰动分析法、似然比估计法[2]以及Malliavin积分法[3]等提高Monte Carlo模拟运算效率及估计精度的方法。

算术亚式期权价格敏感度的估计难点主要体现在无法找到对数正态分布样本算术平均的分布函数解析表达式。如果获得了这一分布函数的解析表达式或者近似表达式，就可以像分析几何平均亚式期权一样对算术平均亚式期权进行敏感度分析。针对这一问题，很多算术平均分布函数的近似估计被提出。Turnbull等(1991)[4]以及Levy(1992)[5]先后用艾吉沃斯序列(Edgeworth series)的扩展形式去拟合一个对数正态随机分布的概率密度函数。研究结果发现：这种方法有其适用条件和缺陷，即当标的资产波动率较低、期权到期时间较短时，敏感性参数估计结果有很好的表现，且利用此方法无法度量出估计值误差。为了解决对算术平均亚式期权敏感度估计误差的识别及控制问题，一些学者开始探索敏感度估计值的上界及下界，如Curran(1994)[6]、Rogers等(1995)[7]、Kaas等(2000)[8]、Dhaene等(2002)[9]。与此同时，部分学者通过寻找算术平均亚式期权价格显式表达式或者用一些函数替代来对亚式期权的敏感度进行分析。其中，贡献最大的当属Yor(1992)[10]利用Hartman-Watson理论将算术亚式期权价格采用三重积分形式表达。这种方法可通过拉普拉斯变换将问题转化为数值形式，但是与艾吉沃斯序列方法相反，该方法在波动率与到期时间数值较小的情形下，数值解表现得十分不稳定。此后，Geman等(1995)[11]将快速傅里叶变换技术(fast Fourier inversion technique)用于亚式期权的敏感度分析之中。Abate等(1995)[12]分别利用欧拉方程和Post-Widder定理分析亚式期权的敏感度，Fu等(1999)[13]等人曾对类似的方法做过总结。Ju(2002)[14]对亚式期权价格的波动率进行泰勒展开(Taylor expansion)，从而对亚式期权的敏感度进行估计，这种方法很容易地移植到其他奇异期权敏感度相关问题研究中。Dufresne(2000)[15]与Linetsky(2004)[16]分别利用了Laguerre序列展式对算术平均亚式期权的敏感度等问题展开研究。除此之外，Zhang(2001,2003)[17-18]、D’Halluin等(2005)[19]的二叉树方法也是用于分析亚式期权敏感度的重要方法。Boyle等(2008)[20]在关于亚式期权敏感度分析中总结了对亚式期权敏感度估计的方法，并指出尽管控制变量方法在对亚式期权价格的估计中发挥了很好的作用，但是并不能改进对亚式期权敏感度的估计。

目前，国内对算术平均亚式期权敏感度的相关研究几乎是空白。刘海媛(2006)[21]推导了几何亚式期权的敏感度的计算公式。董成(2011)[22]采用拟蒙特卡罗(QMC)方法和蒙特卡罗(MC)方法，结合各种生成路径，对比分析了亚式期权敏感度模拟结果。

Kemna等(1990)[23]在对算术平均亚式期权价格的估计中曾使用了控制变量方法，将几何平均亚式期权价格的解析解作为控制变量，从而提高了算术平均亚式期权价格Monte Carlo模拟的效率和精度。借鉴这一思路，本文将利用几何平均亚式期权敏感度的Delta解析表达式，试图作为控制变量来提高算术平均亚式期权敏感度的Monte Carlo估计精度及模拟效率。

三、敏感性参数估计方法

(一)控制变量的构建

敏感性参数具体包括Delta、Vega、Rho等，分别代表期权价格对标的资产价格、标的资产价格波动率、无风险利率的偏导数。本文将重点讨论亚式期权Delta的估计方法，对于其他敏感性参数可以通过类似方法进行讨论。在经典Black-Scholes模型假定背景下，标的资产价格S(t)服从几何布朗运动，其价格与时间满足如下关系：

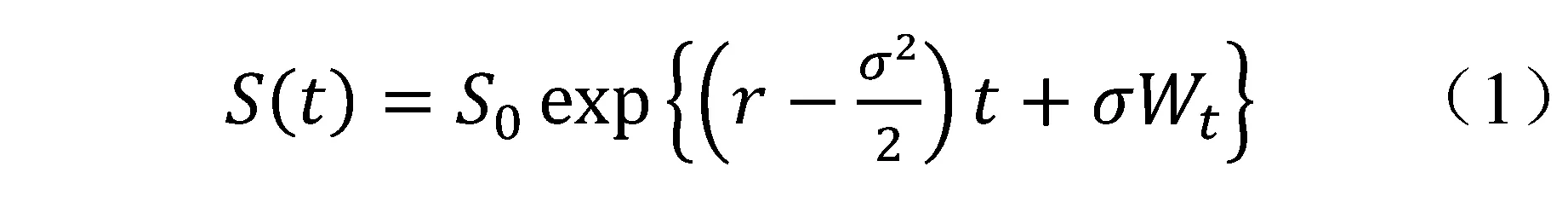
其中：r为无风险利率，σ代表资产价格波动率，Wt是维纳过程。对于普通的欧式看涨期权或看跌期权，可以利用Black-Scholes公式给出期权价格的解析解。而对于算数平均亚式期权，期权价格以及相应的价格敏感度的解析解是不存在的，可以利用几何平均亚式期权价格敏感度的解析解来帮助优化算数平均亚式期权价格敏感度的估计。下面给出几何平均亚式期权价格对于标的资产价格敏感度Delta(简记为Δ)的解析表达式，以Δ为例讨论如何利用控制变量法对期权敏感度估计进行优化。

对于一个随机变量X，当需要估计其数学期望μX=E(X)时，如果存在另外一个期望值已知的随机变量Y，便可以构建估计量：

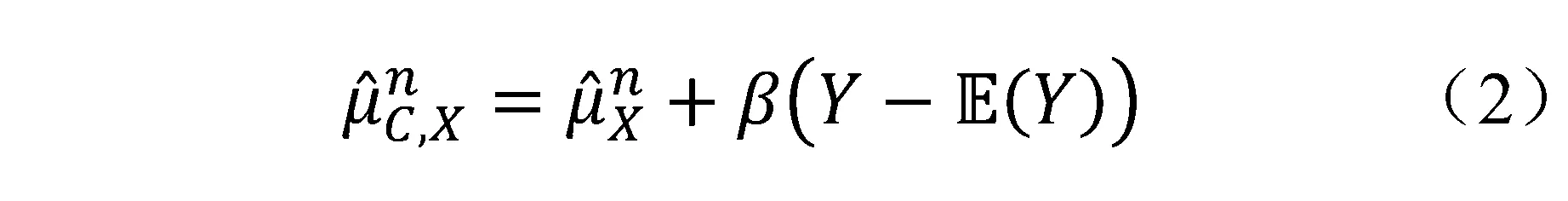
其中：

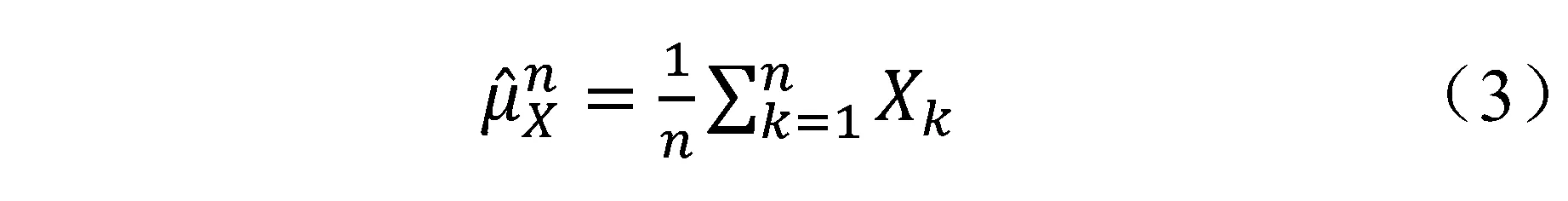
因为

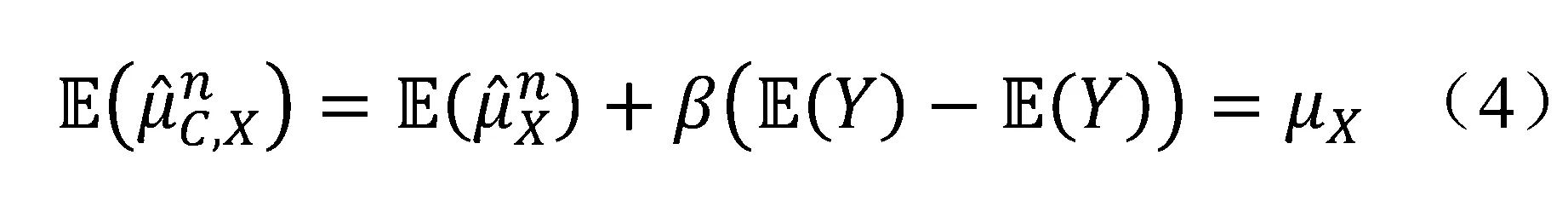
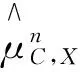
对式(2)两边取方差有

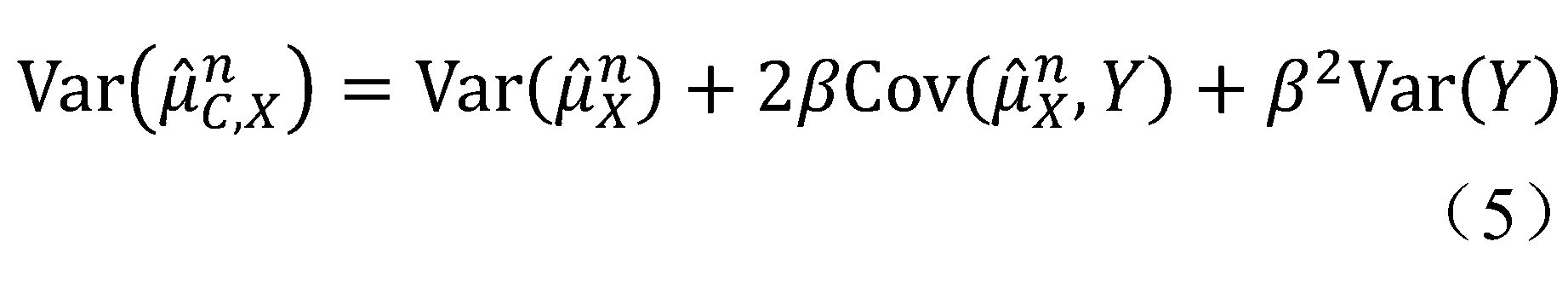
对式(5)计算关于β的导数可得

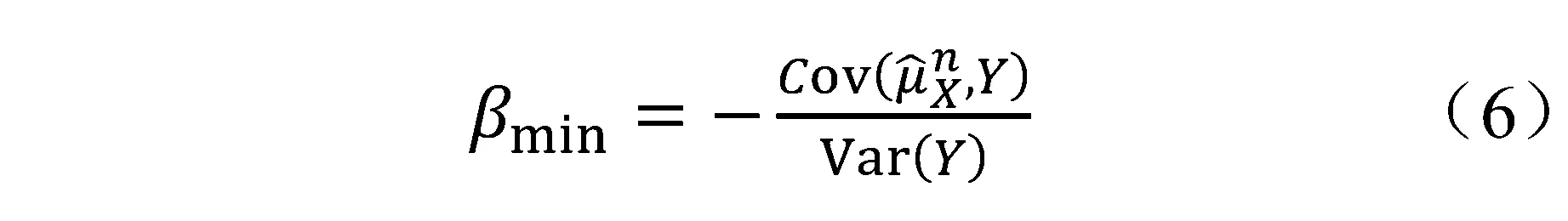
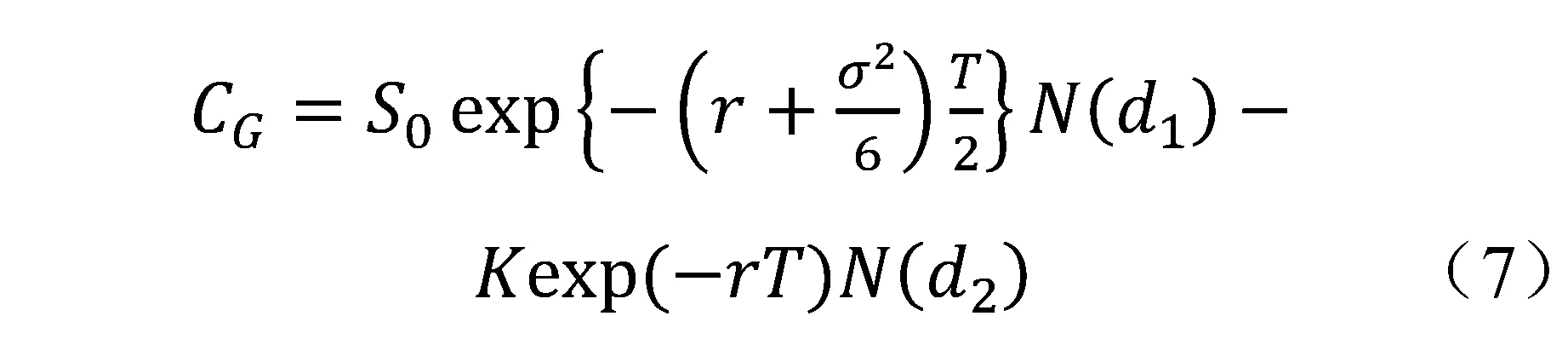
其中:

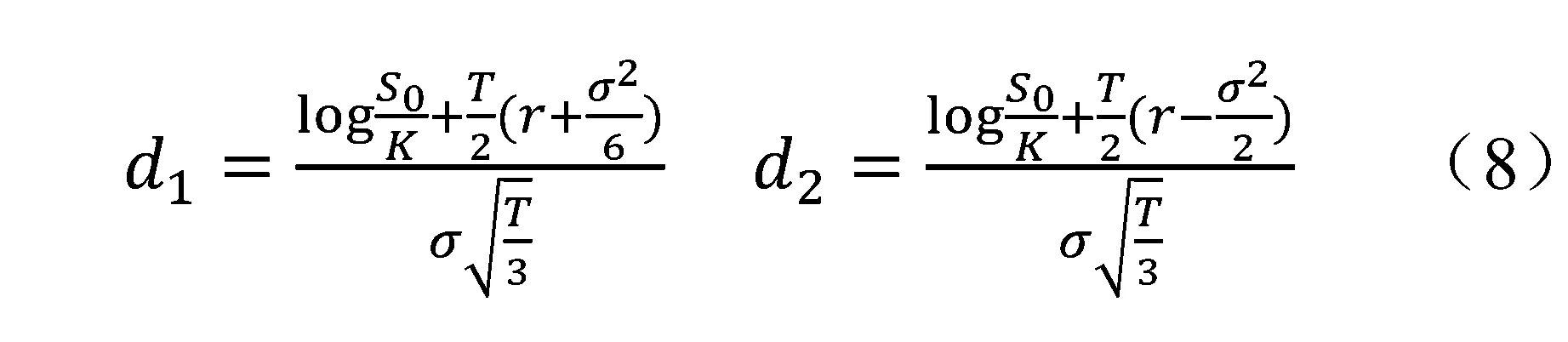
利用上文中给出的关于几何平均亚式期权价格的解析表达式，可以根据链式法则对期权价格求偏导数,得到式(9)：

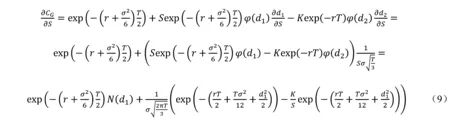
由式(9)可得几何平均亚式期权敏感性参数Delta解析表达式为

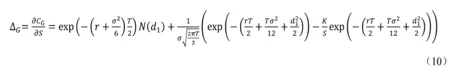
并以此作为控制变量。

因为在风险中性的概率测度下，有

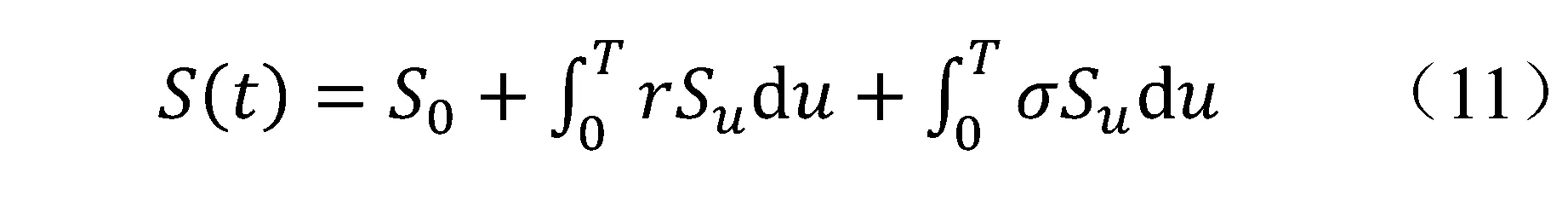
由这一随机微分方程来刻画标的资产的波动，它的解便是通常所说的几何布朗运动

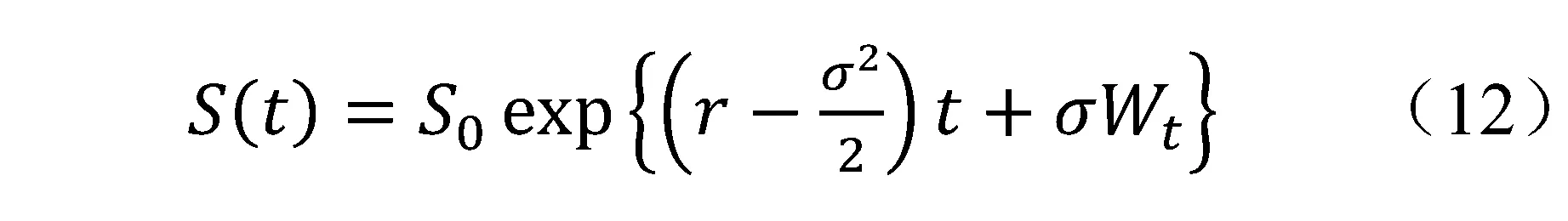
几何平均亚式期权及算术平均亚式期权的收益分别为有

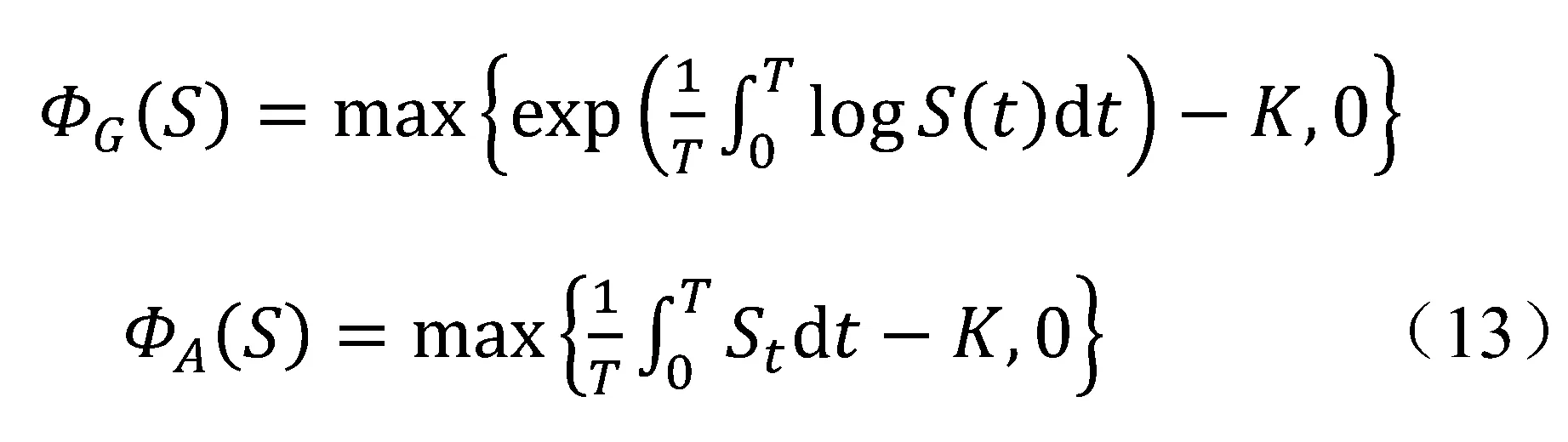
(二)Monte Carlo模拟的理论过程

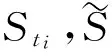
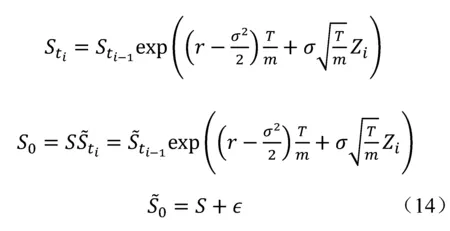
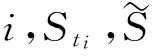
根据Δ的定义，需要讨论当资产价格初值发生变化时，对应的期权价格所发生的变化，并求出二者的比值。

第二步：近似算数平均亚式期权与几何平均亚式期权的到期收益。

首先利用黎曼对期权收益中的积分进行数值近似：

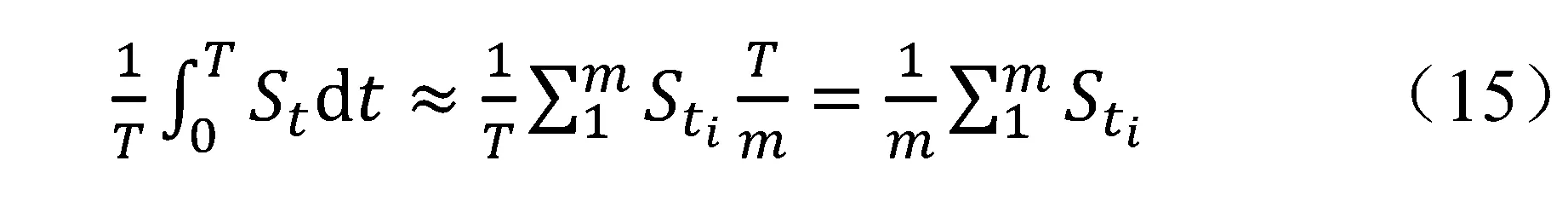
利用Monte Carlo模拟n次资产价格变化的轨迹，从而生成n个期权到期收益。对于算术平均亚式期权，其收益表示为

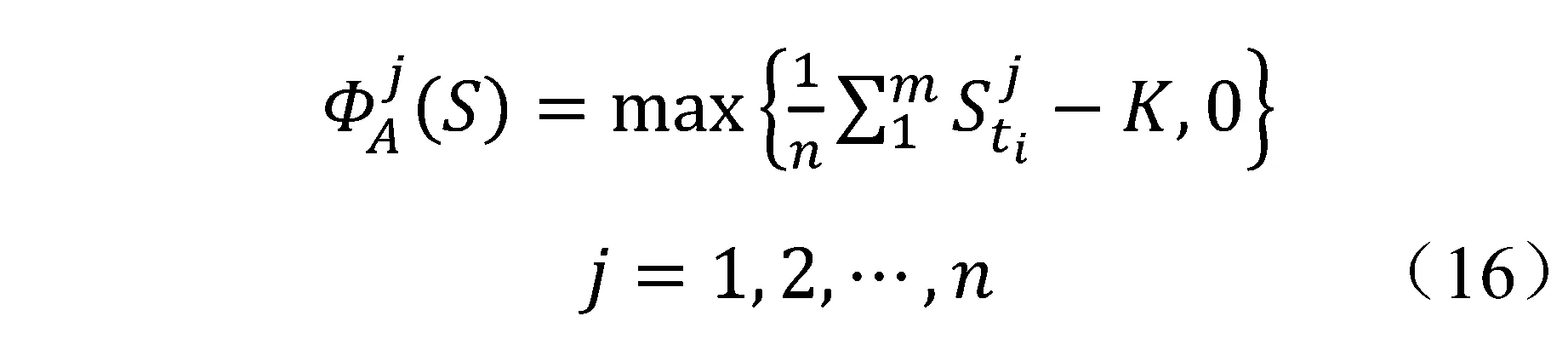
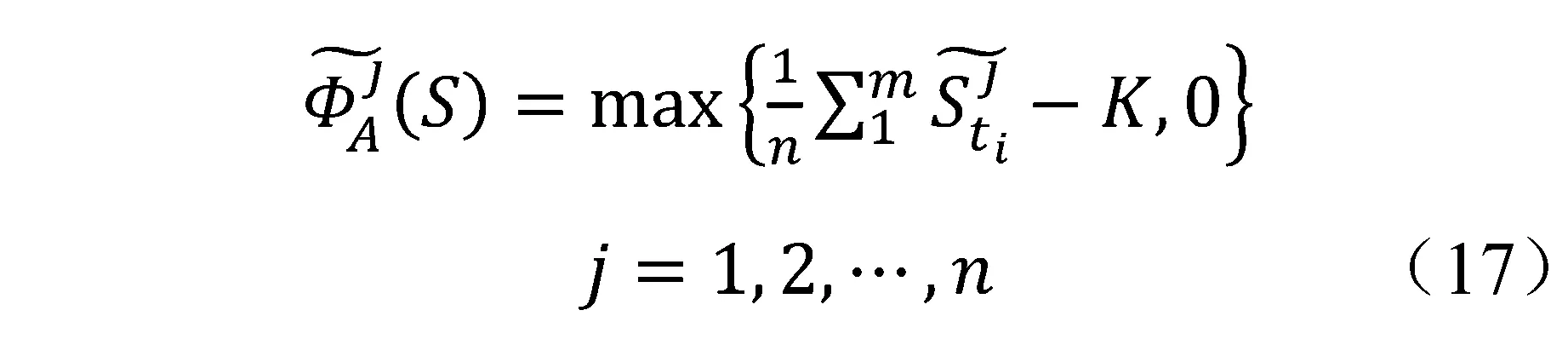
也可以模拟出n个几何平均亚式期权的到期收益：

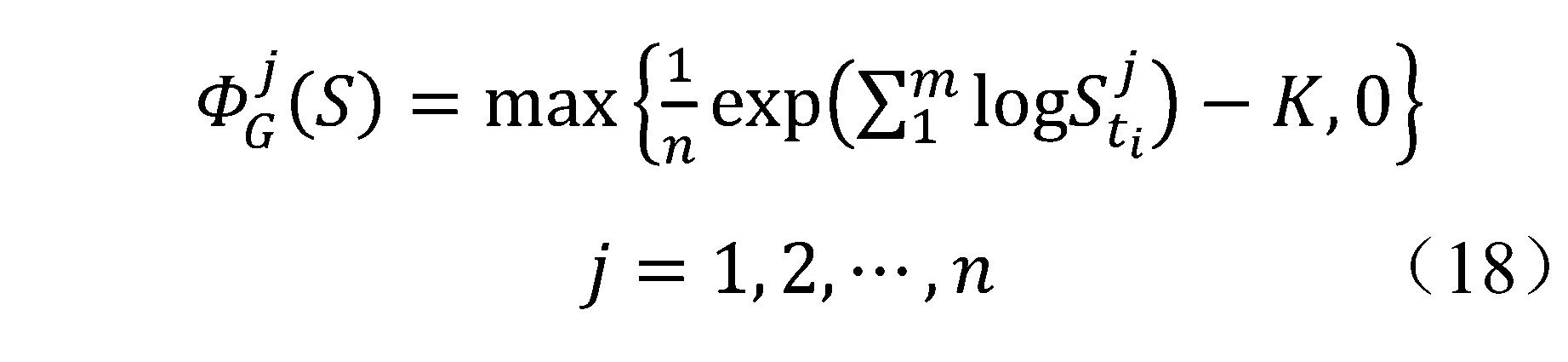
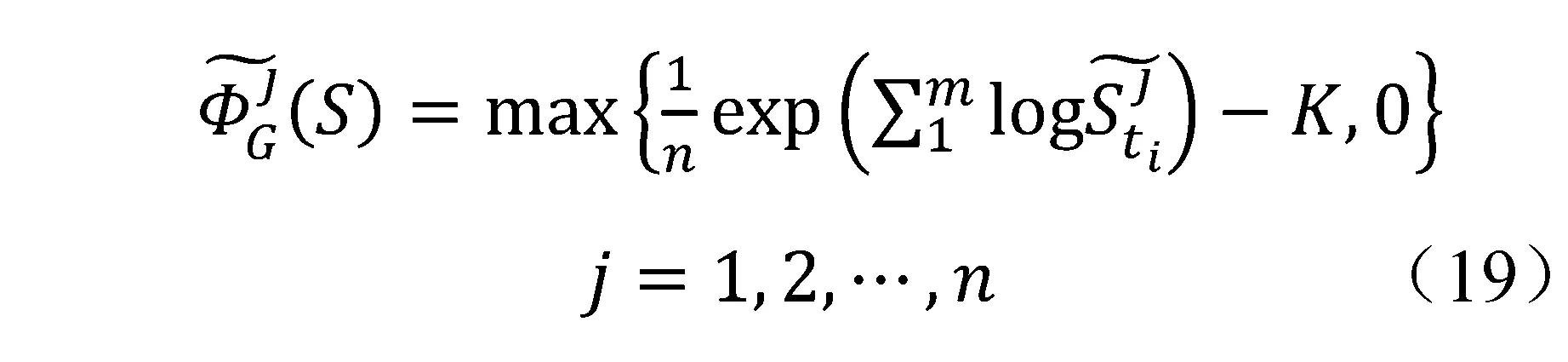
第三步：有限差分逼近,令CA(S)为在Black-Scholes模型下的算数平均亚式期权价格，则有

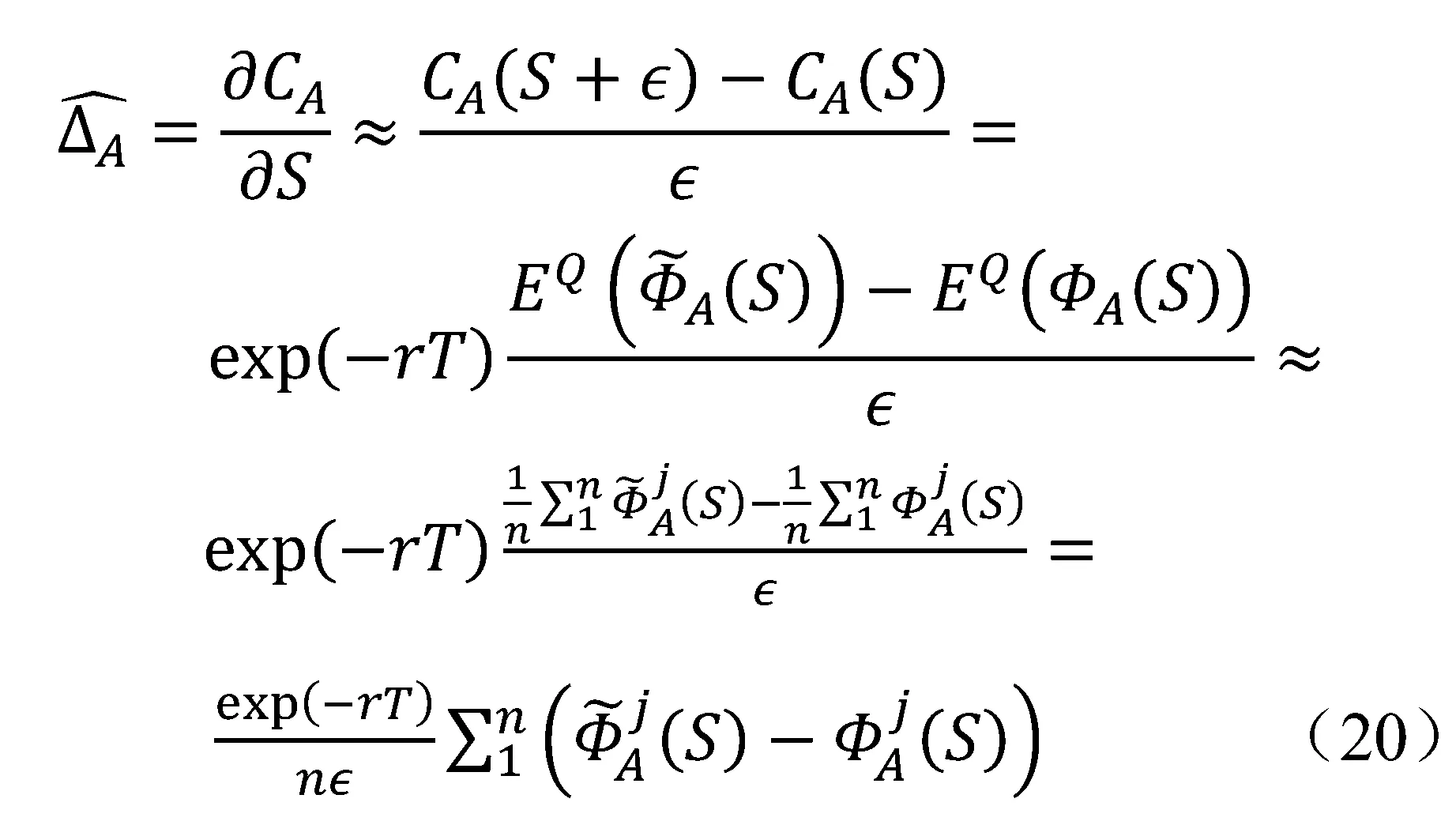
类似的，再给出几何平均亚式期权价格的样本估计量：

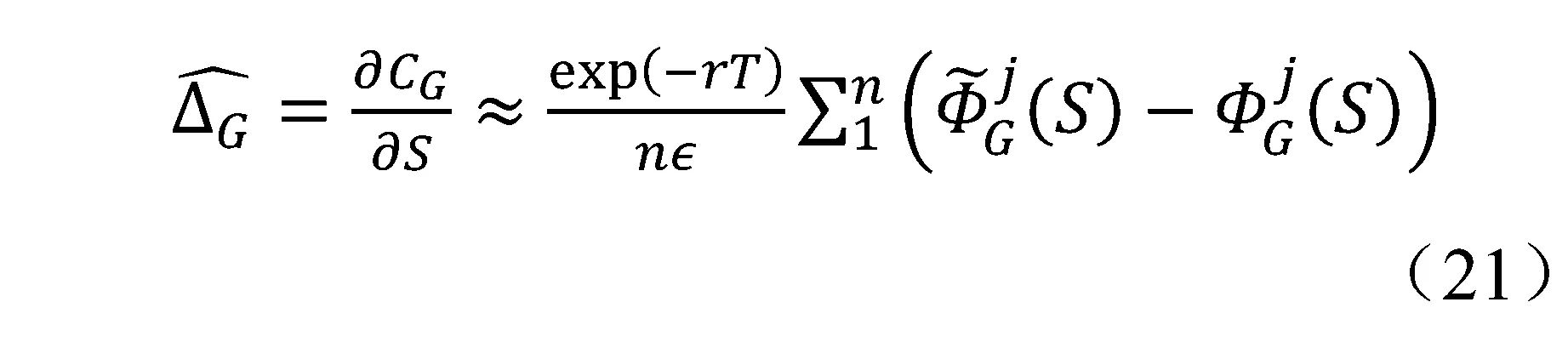
第四步：根据前面推导可以获得算数亚式期权价格敏感性参数估计：

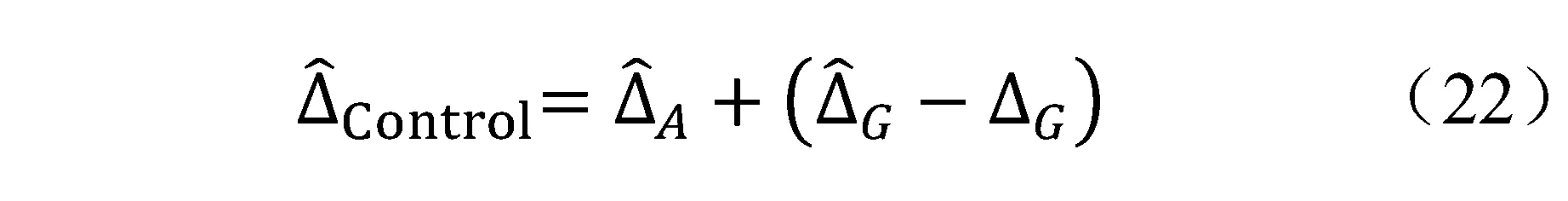
四、Monte Carlo模拟实验

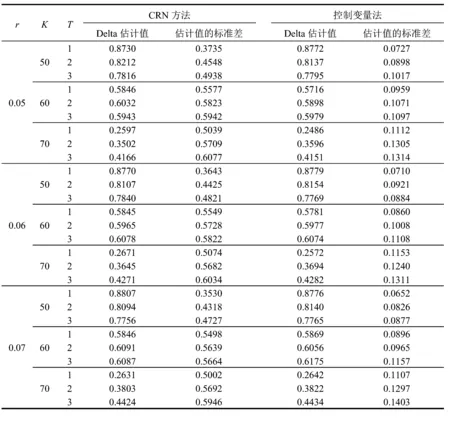
Monte Carlo模拟参数的选择：标的资产初始价格S=60；波动率=0.3;样本大小n=10 000;步数m=500。即将算数平均亚式期权到期时间分为500等分，利用几何布朗运动的性质进行模拟10 000次，分别比较不同利率r、执行价格K以及到期时间T情况下利用控制变量方法与普通的共同随机数方法(CRN)进行模拟的效果。标的资产的波动率假设为0.3，初始价格为60，初始扰动为0.1，即探讨当标的资产价格为60时，价格发生0.1规模的波动时，期权价格发生的变化，如表1所示。

由表1可知：对于算术平均亚式期权敏感度估计结果，控制变量法的Monte Carlo模拟效率高于传统CRN方法，其运算效率显著提高；在估计精度方面，对应不同的利率、执行价格及到期时间，控制变量法得到的估计值标准差明显小于CRN方法，即控制变量的敏感度估计精度更高。

五、结语

本文对算数亚式期权价格的敏感度估计方法进行了研究，根据几何平均亚式期权的敏感性参数解析解，设计控制变量，推导出算术平均亚式期权价格敏感度的无偏估计量，以此进行Monte Carlo模拟实验，得出以下结论：在运算效率方面，通过控制变量方法改进的Monte Carlo模拟运算速度显著优于CRN方法。10 000次模拟利用普通CRN方法运行时间约为5 s，而利用控制变量方法运行时间可以控制在1 s以内。在估计精度方面，控制变量方法同样具有优势，对应不同的利率、执行价格及到期时间，利用控制变量法得到的估计值，标准差均显著小于普通CRN方法。因此，控制变量法在对算术亚式期权价格的敏感度估计、误差控制方面具有比较优势。

表1关于控制变量及CRN方法Monte Carlo模拟的结果

参考文献：

[1]BOYLE P. Options: A Monte Carlo approach[J]. Journal of Financial Economics, 1977, 4(3): 323-338.

[2]BROADIE M, GLASSERMAN P. Estimating security price derivatives using simulation[J]. Management Science, 1996: 42(2): 269-285.

[3]NUALART D. The Malliavin calculus and related topics[M].2nd ed. Berlin: Springer-Verlag, 2006.

[4]TURNBULL S M, WAKEMAN L M. A quick algorithm for pricing European average options[J]. Journal of Financial and Quantitative Analysis, 1991, 26(3): 377-389.

[5]LEVY E. Pricing European average rate currency options[J]. Journal of International Money and Finance, 1992, 11(5): 474-491.

[6]CURRAN M. Valuing Asian and portfolio options by conditioning on the geometric mean price[J]. Management Science, 1994, 40(12): 1705-1711.

[7]ROGERS L, CHRIS G, SHI Z. The value of an Asian option[J]. Journal of Applied Probability, 1995, 32(4): 1077-1088.

[8]KAAS R, DHAENE J, GOOVAERTS M J. Upper and lower bounds for sums of random variables[J]. Insurance: Mathematics and Economics, 2000, 27(2): 151-168.

[9]DHAENE J, DENUIT M, GOOVAERTS M J, et al. The concept of comonotonicity in actuarial science and finance: theory[J].Insurance: Mathematics and Economics, 2002, 31(1): 3-33.

[10]YOR M. On some exponential functionals of Brownian motion[M]//Exponential functionals of Brownian motion and related processes. Berlin: Springer Berlin Heidelberg, 2001: 23-48.

[11]GEMAN H, EYDELAND A. Domino effect[J].Risk,1995, 8(4): 65-67.

[12]ABATE J, WHITT W. Numerical inversion of Laplace transforms of probability distributions[J]. ORSA Journal on Computing, 1995, 7(1): 36-43.

[13]FU M C, MADAN D B, WANG Tong. Pricing continuous Asian options: A comparison of Monte Carlo and Laplace transform inversion methods[J]. Journal of Computational Finance, 1999, 2(2): 49-74.

[14]JU Nengjiu. Pricing Asian and basket options via Taylor expansion[J]. Journal of Computational Finance, 2002, 5(3): 79-103.

[15]DUFRESNE D. Laguerre series for Asian and other options[J]. Mathematical Finance, 2000, 10(4): 407-428.

[16]LINETSKY V. Spectral expansions for Asian (average price) options[J]. Operations Research, 2004, 52(6): 856-867.

[17]ZHANG J E. A semi-analytical method for pricing and hedging continuously sampled arithmetic average rate options[J]. Journal of Computational Finance, 2001, 5(1): 59-80.

[18]ZHANG J E. Pricing continuously sampled Asian options with perturbation method[J]. Journal of Futures Markets, 2003, 23(6): 535-560.

[19]D’HALLUIN Y, FORSYTH P A, VETZAL K R. Robust numerical methods for contingent claims under jump diffusion processes[J]. IMA Journal of Numerical Analysis, 2005, 25(1): 87-112.

[20]BOYLE P, POTAPCHIK A. Prices and sensitivities of Asian options: A survey[J].Insurance: Mathematics and Economics,2008, 42(1): 189-211.

[21]刘海媛.几何亚式期权价格敏感性参数估计[J].徐州工程学院学报,2006(3):44-48.

[22]董成.拟蒙特卡罗方法在亚式期权敏感性参数估计中的应用[D].北京：清华大学,2011.

[23]KEMNA A G Z, VORST A C F. A pricing method for options based on average asset values[J]. Journal of Banking & Finance, 1990, 14(1): 113-129.

收稿日期：2016-03-15

基金项目：国家自然科学基金资助项目(71171035，71471030)；国家青年社会科学基金资助项目(13YJC790185)

作者简介：王维国(1963-),男，博士，教授，博士生导师;E-mail：695795650@qq.com

文章编号：1671-7031(2016)03-0019-06

中图分类号:F224.0

文献标志码：A