爆炸荷载下夹层玻璃曲板的动态响应分析*

张红　邓汉国　姚小虎　龙谦

(华南理工大学 土木与交通学院， 广东 广州 510640)

爆炸荷载下夹层玻璃曲板的动态响应分析*

张红邓汉国姚小虎龙谦

(华南理工大学 土木与交通学院， 广东 广州 510640)

摘要:采用理论与有限元仿真相结合的方法，研究爆炸荷载下夹层玻璃曲板动态响应的计算方法.推导了固支边界夹层玻璃平板的动态响应理论计算方法，发现PVB弹性模量对理论计算精度有重要影响.继而对爆炸荷载下夹层玻璃曲板的动态响应进行了研究，发现夹层玻璃曲板存在两个稳定的曲板系数(CCP)，为曲板动态响应计算提供了一种简化的方法，即根据同样尺寸的夹层玻璃平板动态理论计算最大挠度和最大主应力，相应乘以曲板系数即可预估夹层玻璃曲板的最大挠度和最大主应力.文中还定性分析了夹层玻璃曲板几何参数对曲板系数的影响，拟合得到了经验公式，为夹层玻璃曲板动态响应的预估提供了一种简便、实用的计算方法.

关键词：夹层玻璃曲板；抗爆；曲板系数；动态响应

爆炸事故中，爆炸冲击波作用到建筑玻璃上，产生飞溅的玻璃碎片，是造成人员伤亡的主要原因[1].夹层玻璃被证明是可降低造成人员伤亡风险的一种安全玻璃结构，因而广泛应用于玻璃幕墙.

很多研究者对玻璃幕墙的动态响应进行了研究并取得了一定成果.高轩能等[2]应用弹性薄板振动理论研究框支承玻璃在爆炸冲击荷载下的动力响应，得到玻璃最大挠度与最大应力的计算公式以及安全距离的经验公式，然而玻璃高宽比限制为某常数值，且忽略了爆炸负压段的影响.Chandrasekharappa和Teng等[3- 4]采用冯·卡门非线性板理论以及摄动法求解了弹性板在爆炸荷载下的大挠度动态响应.在大挠度理论的基础上，Birman和Turkmen等[5- 6]采用伽辽金法建立动态方程并采用龙格库塔法求解方程，研究了爆炸冲击下夹层板的动态响应.Wei等[7]采用薄板小挠度理论、大挠度理论以及有限元模拟对爆炸荷载下夹层玻璃板的动态响应进行了分析，研究指出，爆炸负压段影响一般不可忽略.

玻璃幕墙在实际应用中因结构需要，采取曲板形式并不少见，然而关于夹层玻璃曲板在爆炸荷载下的动态响应研究相对很少.借鉴Wei等[7]的研究成果，文中提出了夹层玻璃曲板的动态响应简化计算方法，具有一定工程实用价值.

1理论分析与验证

1.1爆炸荷载计算

空气中爆炸荷载可以描述成一个指数形式的函数表达式[8]：

(1)

式中，cr为正压放大系数，ΔPf为冲击波超压峰值，t+为正压作用时间，α为衰减系数，当时间t大于t+意味着爆炸荷载进入负压段影响阶段.

爆炸超压峰值ΔPf(MPa)为[9]

(2)

式中，Z为

(3)

式中，R为爆炸距离，W为炸药当量.

正压作用时间t+(ms)为[8]

(4)

衰减系数α表示为

α=1.5Z-0.38，0.1≤Z≤30

(5)

正压放大系数为

(6)

式中，p1=ΔPf+p0，环境气压p0约为101.3kPa.

1.2夹层玻璃平板动态计算

矩形夹层玻璃平板结构如图1所示，对固支夹层玻璃动态挠度与应力的有关计算推导如下.

图1　爆炸荷载下矩形夹层玻璃板示意图

Fig.1Schematic diagram rectangular laminated glass panels under blast load

爆炸荷载下夹层玻璃的协调方程和运动方程为[7]

(7)

(8)

式中,F为Airy应力函数，E为等效弹性模量，w为夹层玻璃板的挠度函数，“,xx”是对x求导两次，其他类似.D为等效弯曲刚度，M为单位面积总质量，h为夹层玻璃总厚度,h=ho+hp+hi(hi、ho和hp分别为夹层玻璃内外层玻璃和PVB层的厚度).把3层叠层板等效为单层板，采用等效弹性模量、等效泊松比和横截面应力连续的基本假设，保持总刚度和总质量不变，即

D=Do+Di+Dp

(9)

(10)

(11)

M=ρgho+ρphp+ρghi

(12)

(13)

(14)

式中，Di、Do和Dp分别为夹层玻璃内外层玻璃和PVB层的弯曲刚度，Eg、vg、 ρg和hn分别为玻璃的弹性模量、泊松比、密度和厚度，下标o对应外层玻璃厚度，下标i对应内层玻璃厚度，Ep、vp、 ρp和hp分别为PVB的弹性模量、泊松比、密度和厚度，E和v是等效的弹性模量和泊松比.

(15)

式中，φ(t)为与时间相关的函数.

依据式(15)和(7)可得Airy应力函数F满足：

(16)

经求解可得

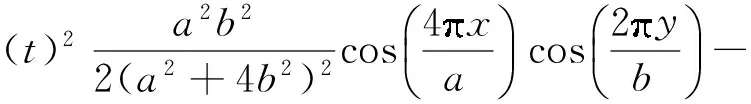
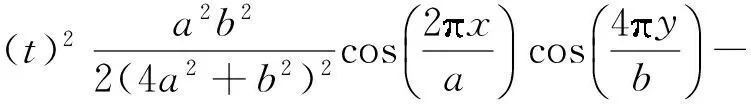
(17)

将运动方程(8)改写成

(18)

采用伽辽金法，则

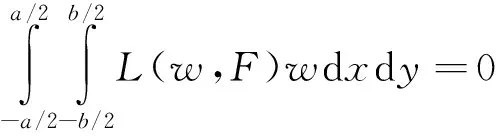
(19)

借助Maple里的4-5阶变步长龙格库塔(Runge-Kutta-Fehlberg)法求解方程.夹层玻璃的应力包括弯曲应力和薄膜应力，即

(20)

(21)

1.3有限元验证

夹层玻璃平板PVB厚度固定为1.52 mm，内外层玻璃等厚度(h)，后续不再说明，几何尺寸为：a=1 400 mm,b=1 200 mm,h=4.76 mm.爆炸荷载工况为：W=15 kg，R=50 m.玻璃和PVB均采取线弹性模型[10- 11]，材料参数如表1所示.

表1　玻璃、PVB材料参数

PVB弹性模量受应变率、使用条件以及温度等影响，在不同文献中的取值有一定波动[12- 14].按理论计算，PVB弹性模量(80～985 MPa)对夹层玻璃动态挠度和应力计算影响非常小(如表2所示，低于1%)，PVB弹性模量对理论计算值不敏感.但是PVB弹性模量对ABAQUS模拟值较为敏感.这是由于PVB弹性模量与玻璃弹性模量差了480倍，PVB贡献的刚度极小，理论的基本假设之一是保持刚度不变；而仿真不仅保持刚度不变，同时考虑了横截面应力不连续的事实，横截面应力分布其实与PVB在内外层玻璃间能传递的剪力有关，即与剪切模量(或弹性模量)密切相关，只有PVB弹性模量足够大，理论上与玻璃弹性模量相等时候，横截面应力才是连续的.

表2理论上PVB弹性模量对平板底部中心挠度和应力的影响

Table 2Theoretical effect of PVB’s elastic modulus on midpoint deflection and stress of laminated glass flat panels

E/MPa挠度/mmσy/MPa804.924332.6451504.924232.6495304.924232.6769854.924032.708

文中推导的固支计算结果与ABAQUS的模拟值的对比如图2和3所示.在夹层玻璃整个动态响应过程中，挠度计算值与ABAQUS模拟值吻合很好，且PVB弹性模量越大，理论计算值与有限元模拟值越吻合，偏差低至1%；PVB弹性模量为150 MPa时，

图2　夹层玻璃平板中心挠度时程曲线

Fig.2Midpoint deflection-time curves of laminated glass flat panels

图3　夹层玻璃平板底部中心应力σy时程曲线

Fig.3Bottom midpoint stress(σy)-time curves of laminated glass flat panels

理论计算值与有限元模拟值偏差约11.1%.这说明PVB弹性模量越大，该理论计算的基本假设(把夹层玻璃等效为单层玻璃板)才越合理，PVB弹性模量是影响理论计算精度的主要因素.同时，夹层玻璃平板的中心处底部应力计算值与模拟值有一定偏差，最大约为37.6%.这主要有两个原因：一是由于固支边界理论推导时，假设的挠度函数w(x,y,t)只取一项，对于夹层玻璃的挠度计算已经趋于收敛，具有很好的精度，对于应力计算，需要对挠度函数w(x,y,t)求导，故需要更高阶的项，因此造成应力的计算有所偏差；二是PVB弹性模量取值150 MPa(浮法玻璃弹性模量72 000 MPa)，夹层玻璃是复合结构，不是整体结构，横截面应力不连续，按理论的应力(假设等效成单层板)计算存在偏差.但总体来说，应力的计算精度是可以接受的.

2夹层玻璃曲板分析

2.1曲板系数A和B

曲板形状各异，文中假设曲板截面是半椭圆，如图4所示，弯曲方向沿长边，短边方向曲率为0，弯曲的程度采用Δd/a的比值表示，Δd为曲板外凸高度，a为长边跨长，b为短边长度.Δd/a值越大，曲板形状越弯曲.

图4　夹层玻璃曲板示意图(1/4模型)

从图5所示夹层玻璃曲板在爆炸荷载下动态响应时程曲线发现：由于整体刚度增大，曲板中心处挠度峰值会降低，表现为振动周期减小.板边(曲边)中心处最大主应力(取绝对值最大的主应力)峰值亦具有同样现象.

图5　最大挠度时程曲线

从表3可以发现：曲板夹层玻璃在爆炸荷载下的动态响应具有一个重要规律——曲板系数A和B波动不大(约9%增幅)；随着爆炸荷载的增加，即炸药当量W的增加，最大挠度和最大主应力均增加，曲板系数A和B会增加.但考虑到玻璃是弹脆性材料，屈服应力大约为60～150 MPa，过大的爆炸荷载下玻璃早就破坏.因而，在夹层玻璃未发生破坏的阶段，曲板系数A和B具有相当稳定的值，分别为0.69和0.70左右(取表中3个值的平均值)，波动分别为6.7%和1.7%.

表3不同爆炸荷载下夹层玻璃的曲板系数1)(R=100 m，

Δd/a=15/400)

Table 3CCP of laminated glass curved panels under different blast loads(R=100 m，Δd/a=15/400)

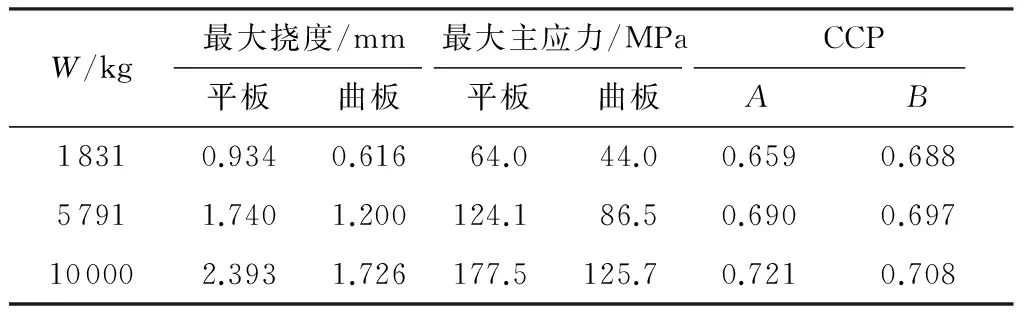
W/kg最大挠度/mm最大主应力/MPaCCP平板曲板平板曲板AB18310.9340.61664.044.00.6590.68857911.7401.200124.186.50.6900.697100002.3931.726177.5125.70.7210.708

1)夹层玻璃平板尺寸：a=400 mm，b=300 mm,h=3 mm.最大挠度为正值，表示爆炸负压段影响不显著，最大挠度取挠度时程曲线第1个峰值.

曲板系数A和B具有相当稳定的值，这具有一般性，在不同的尺寸、不同的爆炸距离以及炸药当量和不同的弯曲程度(Δd/a)下，曲板系数如表4所示.但是，当R=1.5 m时，爆炸负压段影响显著，导致最大挠度发生在夹层玻璃板振动反弹阶段，曲板系数A和B分别偏离稳定值0.30和0.37.有关爆炸负压段影响的研究可参阅文献[16].

表4不同爆炸荷载下夹层玻璃的曲板系数1)(Δd/a=100/1 000)

Table 4CCP of laminated glass curved panels under different blast loads(Δd/a=100/1 000)

R/mW/kg最大挠度/mm最大主应力/MPaCCP平板曲板平板曲板AB1.50.128-5.913-2.522143.8101.80.4260.70855.02502.8240.84381.230.50.2980.376100.020003.4211.00798.837.00.2940.374

1)夹层玻璃平板尺寸：a=1 000 mm，b=700 mm,h=6 mm.最大挠度为负值，表示爆炸负压段影响显著，最大挠度发生在夹层玻璃板震动反弹阶段.

因此，当爆炸荷载不足以使玻璃破坏，且爆炸负压可忽略不计时，可推断：曲板系数(CCP)A和B与爆炸荷载相关性较小，主要由夹层玻璃尺寸以及弯曲程度决定.将爆炸荷载简化成三角形荷载，对曲板系数A和B影响很小，再次验证了这两个系数与爆炸荷载相关性较小的事实，如表5所示.

表5简化三角形爆炸荷载下夹层玻璃的曲板系数

Table 5CCP of laminated glass curved panels under simplified triangle blast loads

P/kPat+/ms尺寸/mmΔd/aAB8017a=400,b=300,h=315/4000.7060.7036016a=1000,b=700,h=6100/10000.3130.376

2.2参数研究

定性分析夹层玻璃尺寸和弯曲程度对曲板系数的影响，可以发现参数之间是耦合的，影响趋势以及部分耦合分析如下：

(1) 同样夹层玻璃尺寸下，曲板弯曲程度越大，曲板系数越小，曲线不可偏移得到，弯曲程度对曲板系数的影响受玻璃厚度影响，如图6所示.

图6　曲板系数A随弯曲程度的变化曲线

(2) 同样曲板弯曲程度和法向投影面积下，玻璃厚度越大，曲板系数越大且受弯曲程度耦合影响，如图7所示.

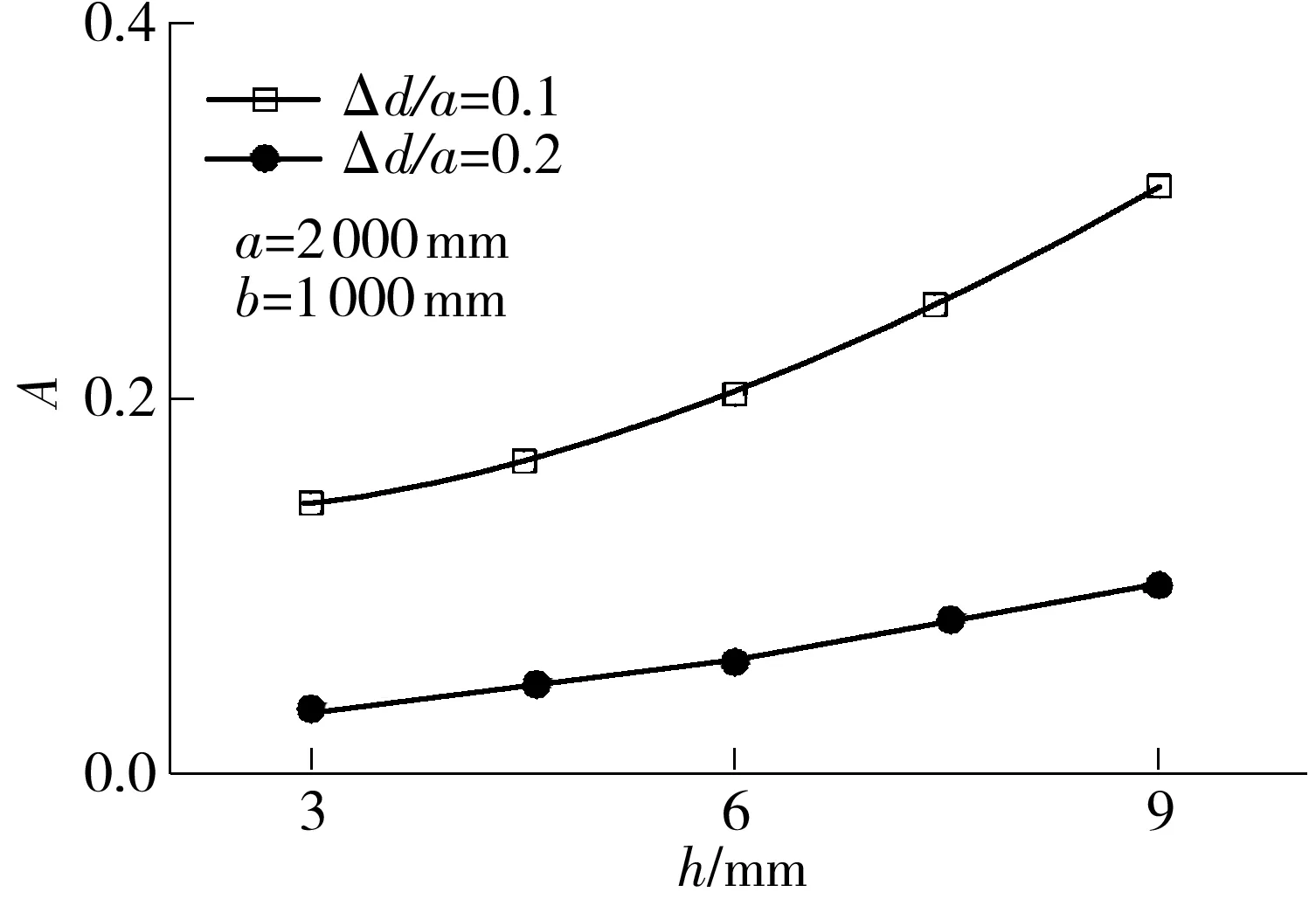
图7　曲板系数A随玻璃厚度的变化曲线

(3)同样玻璃厚度下，法向投影面积越大，曲板系数越小，如图8所示.

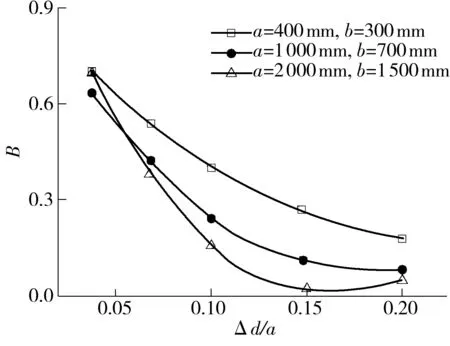
图8　曲板系数B随法向投影面积的变化曲线(h=3 mm)

Fig.8Curves ofBchanging with normal projection area(h=3 mm)

(4)同样玻璃厚度、长度和弯曲程度下，宽长比值越大，曲板系数一直降低或者先降后增，如图9所示.宽长比值对曲板系数的影响是非常复杂的，受弯曲程度耦合影响.

图9　曲板系数B随宽长比值变化曲线

2.3经验公式

玻璃厚度分别为3、6和9 mm，长分别为400、1 000和2 000 mm，对于任意长度，宽度也含有4种情况以考虑不等边矩形夹层玻璃，曲板弯曲程度(k=Δd/a)为0、0.037 5、0.1和0.2，共计3×3×4×4=144种情形.在定性分析的基础上，依据曲板系数A和B与夹层玻璃尺寸的关系,采用1stOpt里的麦夸特法(LM)和通用全局优化法拟合系数，经拟合得出曲板系数A和B经验公式为

(22)

(23)

式中，A和B随玻璃厚度h增加而增加，随投影面积a×b增加而减小，这与定性分析参数的影响是一致的，可见拟合是合理的，且拟合的效果很好.曲板系数A的决定系数为0.978，相关系数为0.990；曲板系数B的决定系数为0.975，相关系数为0.988.如表6所示，对于绝大部分数据吻合较好(低于10%)，有少数数据存在较大偏差(10%～20%)，假设的拟合函数基本合理.仅有少数几个数据拟合失真，这可能是假设的拟合函数未能完全描述系数随尺寸变化规律导致的，且参数之间存在耦合影响，不容易分析出假设经验公式的形式，假设不够合理.

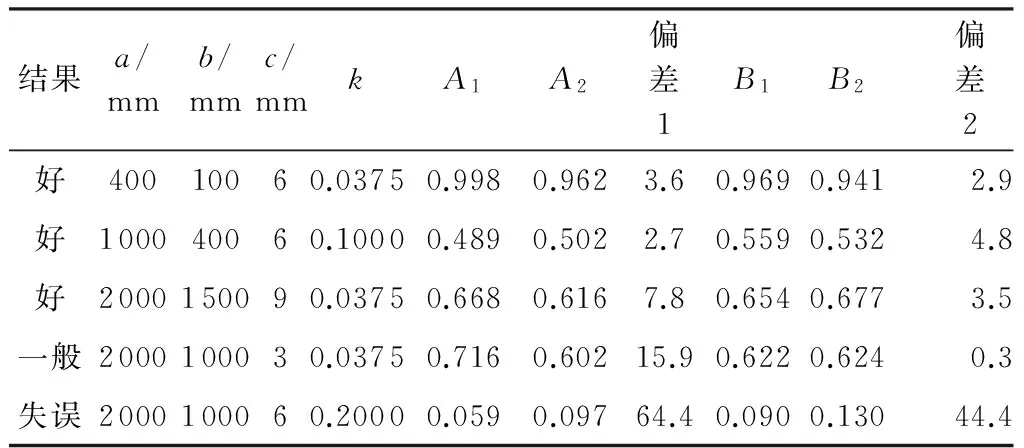
表6　经验公式拟合校核1)

1)A1、B1表示原始数据，A2、B2表示拟合数据，偏差1和2分别为A1与A2、B1与B2的偏差.

下面取3个夹层玻璃尺寸(不用于拟合曲板系数A和B经验公式)的挠度以及最大主应力峰值与曲板系数拟合公式预估的进行对比，如表7所示.可以发现，随机选取的几个尺寸在爆炸荷载下(W=120 kg，R=55 m)，预测的最大主应力值(夹层玻璃平板仿真模拟值乘以曲板系数B)与夹层玻璃曲板仿真模拟得到的结果吻合较好，预测的最大挠度(夹层玻璃平板仿真模拟值乘以曲板系数A)与曲板仿真模拟得到的结果可能存在一定偏差，而预测的最大挠度(夹层玻璃平板动态理论计算值乘以曲板系数A)与曲板仿真模拟得到的结果可能存在较大偏差.综合分析理论计算值与有限元仿真的误差，可以发现：主要是由于理论计算的误差(约10%～20%)和曲板系数拟合公式的误差共同引起的，可导致误差变大或者变小.由于误差总体不大，可以看出，曲板系数拟合公式具备一定可靠性和实用性.

表7　经验公式可靠性校核1)

1)w为曲板仿真模拟的最大挠度，w1是采用夹层玻璃平板动态理论计算值乘以曲板系数A得到，w2是采用夹层玻璃平板有限元仿真值乘以曲板系数A得到；σc是曲板仿真模拟的最大主应力，σf采用平板有限元仿真结果(理论计算应力误差太大)乘以曲板系数B得到，偏差1是w1和w2与w的偏差，偏差2是σf与σc的偏差.

因此，当爆炸荷载不足以使玻璃破坏，且爆炸负压可忽略不计时，爆炸荷载下夹层玻璃曲板的动态计算可以采取简化计算方法，即根据同样尺寸的夹层玻璃平板动态理论计算最大挠度和最大主应力，乘以曲板系数A和B即可预估夹层玻璃曲板的最大挠度和最大主应力.同时，提高夹层玻璃平板动态理论计算的精度，对提高夹层玻璃曲板动态响应预估的精度是十分必要的.

3结论

文中推导了固支边界夹层玻璃平板的动态理论计算方法，发现PVB弹性模量对理论计算精度有重要影响，即PVB弹性模量越大，把夹层玻璃等效为单层玻璃板的假设越加合理，理论计算精度越高.

当爆炸荷载不足以使玻璃破坏，且爆炸负压影响可忽略不计时，结论如下：①夹层玻璃曲板存在两个稳定的曲板系数(CCP)A和B，系数与玻璃尺寸以及弯曲程度k有关，与荷载相关性很小；②曲板动态响应计算可采取文中的简化计算方法，预估夹层玻璃曲板的最大挠度和最大主应力.

参考文献：

[1]BRUCK T.The economic consequences of the new global terrorism [J].Economic Bulletin,2002,39(10):327- 332.[2]高轩能,江媛,王书鹏.建筑玻璃的爆炸动力响应及防爆距离 [J].计算力学学报,2011,28(4):560- 565.

GAO Xua-neng,JIANG Yuan,WANG Shu-peng.Dynamic response of architectural glass to explosion and safe extent research [J].Chinese Journal of Computational Mecha-nics,2011,28(4):560- 565.

[3]CHANDRASEKHARAPPA G,SRIRANGARAJAN H R.Nonlinear response of elastic plates to pulse excitations [J].Computers & Structures,1987,27(3):373- 378.

[4]TENG T L,LIANG C C,LIAO C C.Transient dynamic large-deflection analysis of panel structure under blast loading [J].JSME International Journal,Ser A,1995,39(4):591- 597.

[5]BIRMAN V,BERT C W.Behaviour of laminated plates subjected to conventional blast [J].International Journal of Impact Engineering,1987,6(3):145- 155.

[6]TURKMEN H S,MECITOGLU Z.Nonlinear structural response of laminated composite plates subjected to blast loading [J].Aiaa Journal,1999,37(12):1639- 1647.

[7]WEI Jun,DHARANI Lokeswarappa R.Response of lamina-ted architectural glazing subjected to blast loading [J].International Journal of Impact Engineering,2006,32(12):2032- 2047.

[8]TEICH M,GEBBEKEN N.The Inflence of the under pressure phase on the dynamic response of structures subjected to blast loads [J].International Journal of Protective Structures,2010,1(2):219- 234.

[9]SADOVSKIY M A.Mechanical effects of air shockwaves from explosions according to experiments [M].Moscow:Nauka Press,2004.

[10]AMADIO Claudio,BEDON Chiara.Blast analysis of la-minated glass curtain walls equipped by viscoelastic dissipative devices [J].Buildings,2012,2(3):359- 383.

[11]IWASAKI R,SATO C,LATAILLADE J L,et al.Experimental study on the interface fracture toughness of PVB(polyvinyl butyral)/glass at high strain rates [J].International Journal of Crashworthiness,2007,12(3):293- 298.

[12]HIDALLANA-Gamage H D,THAMBIRATNAM David P,NIMAL J Perera.Computational analysis of laminated glass panelsunder blast loads a comparison of two dimensional [J].The International Journal of Engineering and Science,2013,2(8):69- 79.

[13]LARCHER,SOLOMOS Martin,CASADEI George,et al.Experimental and numerical investigations of laminated glass subjected to blast loading [J].International Journal of Impact Engineering,2012,39(1):42- 50.

[14]戎文杰,陈素文.国内外PVB材性研究 [J].高分子通报,2012,42(5):82- 87.

RONG Wen-je,CHEN Su-wen.Research on material properties of PVB at home and abroad [J].Polymer Bu-lletin,2012,42(5) :82- 87.

[15]韩强,黄小清,宁建国.高等板壳力学 [M].北京：科学出版社.2002.

[16]张红,邓汉国,姚小虎.夹层玻璃抗爆设计W-R法 [J].华南理工大学学报(自然科学版),2015，43(11)：119- 126.

ZHANG Hong.DENG Han-guo,YAO Xiao-hu,et al.W-Rmethod for blast resistant design of laminated glass [J].Journal of South China University of Technology(Natural Science Edition),2015，43(11)：119- 126.

Analysis of Dynamic Responses of Curved Laminated Glass Panels Under Blast Loads

ZHANGHongDENGHan-guoYAOXiao-huLONGQian

(School of Civil Engineering and Transportation, South China University of Technology,Guangzhou 510640, Guangdong, China)

Abstract:This paper deals with the calculation of dynamic response of curved laminated glass panels under blast loads by means of theoretical analyses and finite element simulation. In the investigation, first, the theoretical calculation methods of dynamic responses of flat laminated glass panels with clamped boundary are deduced, finding that the PVB elastic modulus greatly influences the accuracy of theoretical calculation. Then, the dynamic responses of curved laminated glass panels under blast loads are discussed, finding that there are two stable coefficients of curved panels(CCP), which may provide a simplified method for the dynamic response calculation of curved laminated glass panels, that is, to obtain the maximum deflection and principal stress of curved laminated glass panels by multiplying the corresponding values of flat laminated glass panels in the same size with some coefficients. Meanwhile, the influences of geometric parameters of the curved laminated glass panels on the CCP are quantitatively ana-lyzed, and reliable empirical formulas are fitted. This research provides a simple and practical calculation method for estimating the dynamic responses of curved laminated glass panels.

Key words:curved laminated glass panel; blast resistance; coefficient of curved panel; dynamic response

收稿日期:2015- 08- 24

*基金项目:国家自然科学基金资助项目(11372113)

Foundation item:Supported by the National Natural Science Foundation of China(11372113)

作者简介:张红(1967-),女,博士,副教授,主要从事复合材料及其结构力学和冲击动力学研究.E-mail:emhzhang@scut.edu.cn

文章编号:1000- 565X(2016)04- 0135- 08

中图分类号：TU 382

doi：10.3969/j.issn.1000-565X.2016.04.020