关于方程Zt(p)=p的解
2016-07-02吴成晶
吴成晶,李 华
(西安航空学院 理学院,陕西 西安 710077)
关于方程Zt(p)=p的解
吴成晶,李华
(西安航空学院 理学院,陕西 西安 710077)
摘要:伪Smarandache-totient函数的相关性质研究是初等数论研究的一个重要问题,受到很多学者关注。文章用初等方法给出了关于伪Smarandache-totient函数的方程Zt(p)=p,p为素数的所有解。
关键词:伪Smarandache-totient函数;Euler函数;初等方法
0引言
关于伪Smarandache-totient函数已得到许多结论,例如Zt(n)既不可加也不可乘,即当(m,n)=1时
Zt(m+n)≠Zt(m)+Zt(n),
Zt(mn)≠Zt(m)Zt(n)
本文所要研究的是寻求方程Zt(p)=p的所有正整数解,其中p为素数。
对于60以内的Zt(n)的值,我们发现有两个解[2]
Zt(2)=2,Zt(5)=5.
本文给出该方程的所有解,并给出定理的证明。
1定理及证明
定理1p为素数,若
则Zt(p)=p.
定理2p为素数,方程
Zt(p)=p
有且仅有两个解,其中
p1=2,p2=5.
这样我们就找到了该方程的所有解,以下给出定理的证明过程。
首先给出定理1的证明.
若Zt(p)=p,即就是p|φ(1)+φ(2)+…+φ(p).
由素数的性质[3]知,要满足上式成立,则存在整数M,使得
φ(1)+φ(2)+…+φ(p)=Mp
再由欧拉函数的性质[4],我们有
φ(1)+φ(2)+…+φ(p)≤1+2+3+…+(p-1)
而
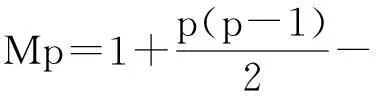
整理之后得到
p2-(2M+1)p+(2-2t)=0.
要使上式有正整数解,则
其中
整理之后,得到
(M+k+1)(M-k)=2(1-t)
p=M+k+1
即
2(1-t)=p(M-k)
得到
p|2(1-t)
由素数的性质[5],解得t=1,所以

Zt(p)=p.
定理1得证。
从上述定理的证明过程中我们可以得到,要使Zt(p)=p,当且仅当t=1,即
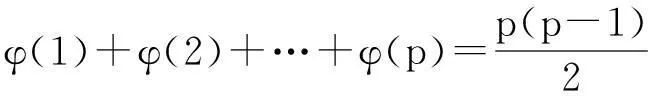
从上述证明过程知道,要使上式成立,对于任意的正整数,1
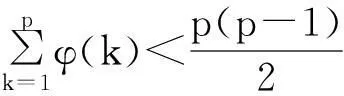
则方程Zt(p)=p在p≥7时是无解的,而易于验证Zt(2)=2,Zt(5)=5.
定理2得证。
2结论
由上述证明过程,我们得到,方程
Zt(p)=p
的所有解只有两个,即:
p1=2,p2=5
而没有其他的解,这样就完整地解决了该方程的解的问题。
参考文献
[1] 潘承洞,潘成彪.初等数论[M].北京:北京大学出版社,2013:141.
[2] Liu Y N,Li L Liu B L.Smarandache Unsolved Problems and New Progress[M].USA:High American Press,2008:91-99.
[3] 张文鹏,李海龙.初等数论[M].西安:陕西师范大学出版社, 2008:41.
[4] 乐茂华.关于Smarandache函数的一个猜想[J].黑龙江大学学报(自然科学版),2007,24(5):687-688.
[5] Lu Y M:On the Solutions of an Equation Involving the Smarandache Function[J].Scientia Magna,2006,2(1):76-79.
[责任编辑、校对:周千]
Solution to the Equation Zt(p)=p
WUCheng-jing,LIHua
(School of Mathematics,Xi′an Aeronautical University,Xi′an 710077,China)
Abstract:Research on the Smarandache-totient function is an important aspect of elementary number theory.Many scholars have paid attention to this problem.The main purpose of this paper is to use the elementary method to give a solution toZt(p)=p,where p represents a prime.
Key words:Smarandache-totient function;Euler function;Elementary method
收稿日期:2016-04-13
作者简介:吴成晶(1987-),女,陕西安康人,助教,从事初等数论的研究。
中图分类号:O156.4
文献标识码:A
文章编号:1008-9233(2016)03-0080-02
