对转涡轮盘腔内各参数变化对转盘壁面摩擦力矩的影响

史学捷,陈淑仙,梁振宇

(中国民用航空飞行学院 航空工程学院，四川 广汉 618307)

对转涡轮盘腔内各参数变化对转盘壁面摩擦力矩的影响

史学捷,陈淑仙,梁振宇

(中国民用航空飞行学院 航空工程学院，四川 广汉 618307)

摘要：对转涡轮盘腔内壁面摩擦力矩的大小直接影响盘腔内气体流动结构和换热效率，进而影响对转涡轮发动机的性能。应用RNG k-ε湍流模型对对转涡轮盘腔内气体流动进行了数值模拟，研究了对转涡轮盘腔间距、中心进气流量、转盘转速的变化对盘腔内壁面摩擦力矩的影响。数值模拟结果表明，盘腔间距在计算范围内的变化对转盘壁面摩擦力矩的影响不明显；转盘壁面摩擦力矩随中心进气流量和转盘转速的增大而增大。

关键词：对转涡轮盘腔；数值模拟；湍流模型；摩擦力矩

0引言

随着航空技术的不断进步，航空飞行器对发动机性能提出了越来越高的要求，如更大的推重比，更低的油耗率和更优异的整机性能等[1]。

对转涡轮技术是一种新型的涡轮气动布局设计，一方面可以使两涡轮转子之间减小导向叶片尺寸或完全省去导向叶片且使转轴缩短，进而大大减小发动机重量，减小气动损失；另一方面使飞机在做回转飞行时，发动机转子上的陀螺力矩大大减小，进而减小发动机传到机身的力矩，提高飞机机动性能[2]。

因此国内外许多国家在研制新型航空发动机的过程中，对对转涡轮技术的研究也越来越重视。GE已经将其应用到实际。如YFl20采用将高低压转子作反向设计，使得飞机飞行时作用于转子上的陀螺力矩会相互抵消大部分，进而减小外传到飞机机身上的力矩[3]。这样，用于冷却涡轮盘,阻止燃气倒灌而密封涡轮盘腔的冷却空气在盘腔内流动并与涡轮盘壁面摩擦产生摩擦力矩，从而影响空气在盘腔内的流动结构，也影响了冷却气流和涡轮盘之间的换热效果。因此深入了解对转涡轮盘腔内各个参数变化对壁面摩擦力矩的影响，对优化盘腔内气体流动结构，提高盘腔内换热效果，提高发动机性能具有重要意义。

目前国内外就对转涡轮盘腔内的流动和换热已经开展了相关的研究工作。Gan[4]对不同转速两个对转涡轮盘进行了实验研究和数值模拟，其实验结果与数值模拟结果比较吻合，从而验证了数值模拟计算的可靠性。Chen[5]对径向出流的对转涡轮盘腔中的换热进行了研究，其所得数据都比同等条件下径向出流的转-静盘腔测得的数据低，证明了对转涡轮盘腔结构的优越性。

蔡毅等[6]在非稳态情况下进行了对转涡轮盘腔内换热特性实验，研究了中心进气量变化对壁面温度和壁面平均努塞尔数的影响，对如何控制进气流量提高涡轮盘腔换热效率有一定指导意义，但就对转盘腔内部流动特性和壁面摩擦力矩的影响没有深入研究。陈淑仙等[7]运用数值模拟的方法对对转盘腔系统内部流动特性进行了模拟计算，仅研究了转速比变化对壁面摩擦力矩的影响，对如何优化对转涡轮盘腔内流动结构的理论支撑还不完善。

由于数值模拟计算费用低、周期短，并能够提供完整的计算结果，因此本文采用数值计算的方法，分析了对转涡轮盘腔内各参数变化对转盘壁面摩擦力矩的影响。

1物理模型、计算方法及验证

1.1物理模型

数值模拟计算对转涡轮盘腔的几何结构[6]，如图1所示。转盘半径R=200mm，盘腔间距H=53mm，出气口间隙S=4mm，中心进气口半径r=20mm,规定进气口所在的转盘为上游盘，另一个转盘为下游盘，上游盘转速为正方向，下游盘转速为负方向。

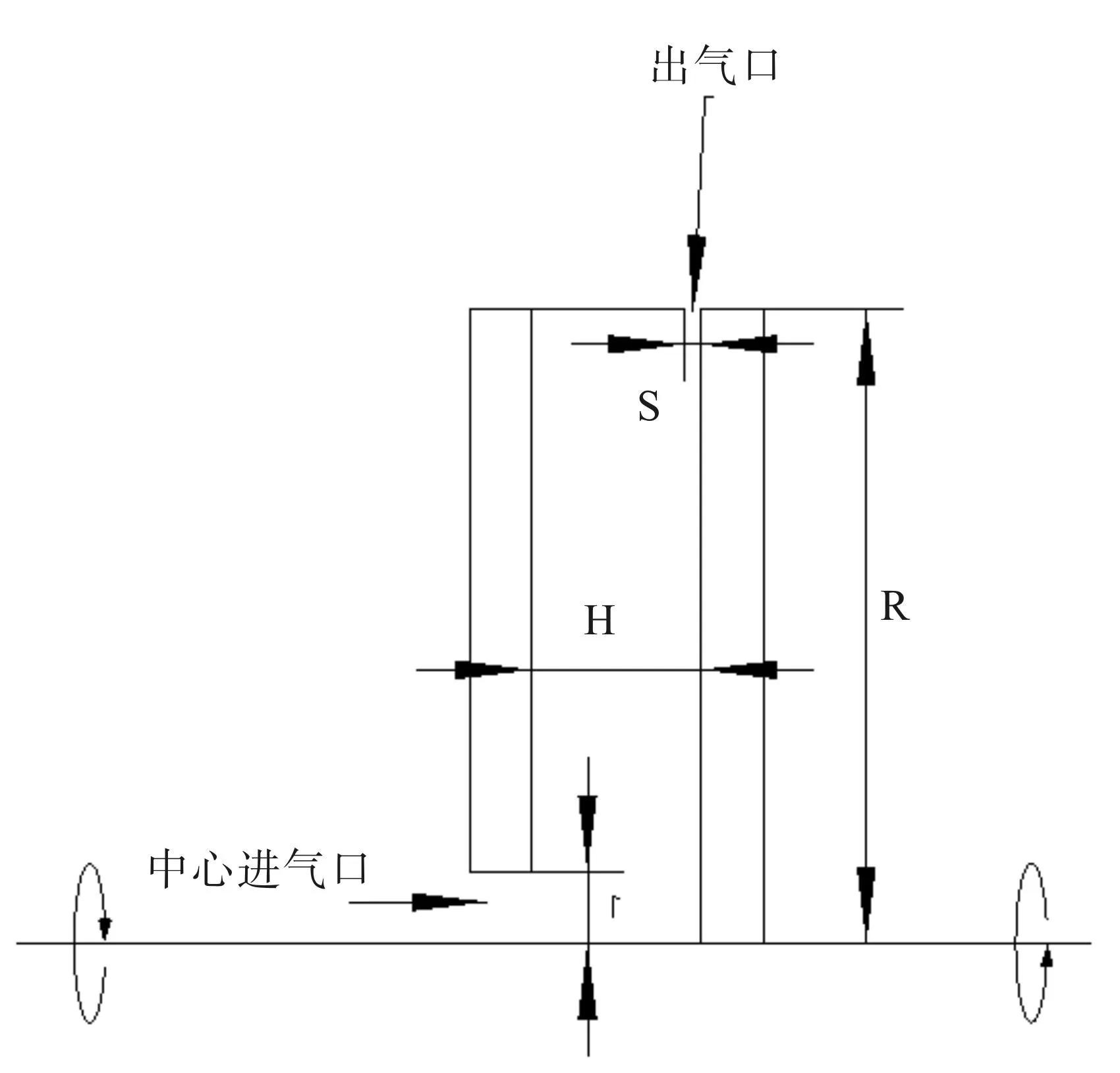
图1　物理模型结构示意图

1.2网格划分

建立与实验台相同的模型，由于采用有限容积法，需要划分网格，模型采用非结构化网格，进气口和出气口进行网格加密，为满足Ekman边界的特点，在两个转盘附近设置间距逐渐增大的网格，故得到近壁面网格是较密的，远壁面网格是均匀的。

1.3控制方程及边界条件设置

三维笛卡尔右手坐标系下的稳态流动和传热方程如公式(1)：

(1)

其中，Γ和S分别为变量u,v,w,T,k,ε对应广义扩散系数和源项[8]。

边界条件如下：

本文结合生产实践，将渣中Fe/Si控制在2.1～2.7，Ca/Si控制在0.4～0.85，最终硅酸度K值控制在1.0～1.3。生产实践结果表明：随着顶吹炉操作工专业技术知识不断积累及操作技能不断提升，铅顶吹炉渣型的有效调整和控制达标有利于抛渣含铅的降低。

(1)入口边界条件采用质量流量入口，进口气温取295K；

(2)出口边界条件采用压力出口，出口气温取295K；

(3)下游盘边缘面则取为热流密度为q=31831W/m2的恒热流边界，其余固体界面设置为绝热边界。

1.4计算方法验证及湍流模型选择

由于各种湍流模型具有不同适用范围，不同的模型依赖于所研究流动状态的具体情况。本文分别选用了标准k-ε湍流模型和RNG k-ε湍流模型对文献[6]中的实验工况进行了数值模拟，其实验工况为：上游盘转速+1000rpm，下游盘转速-1000rpm，中心进气量500kg/h，室温295K。上游盘和下游盘为数值模拟值与实验值的对比，如图2和图3所示。

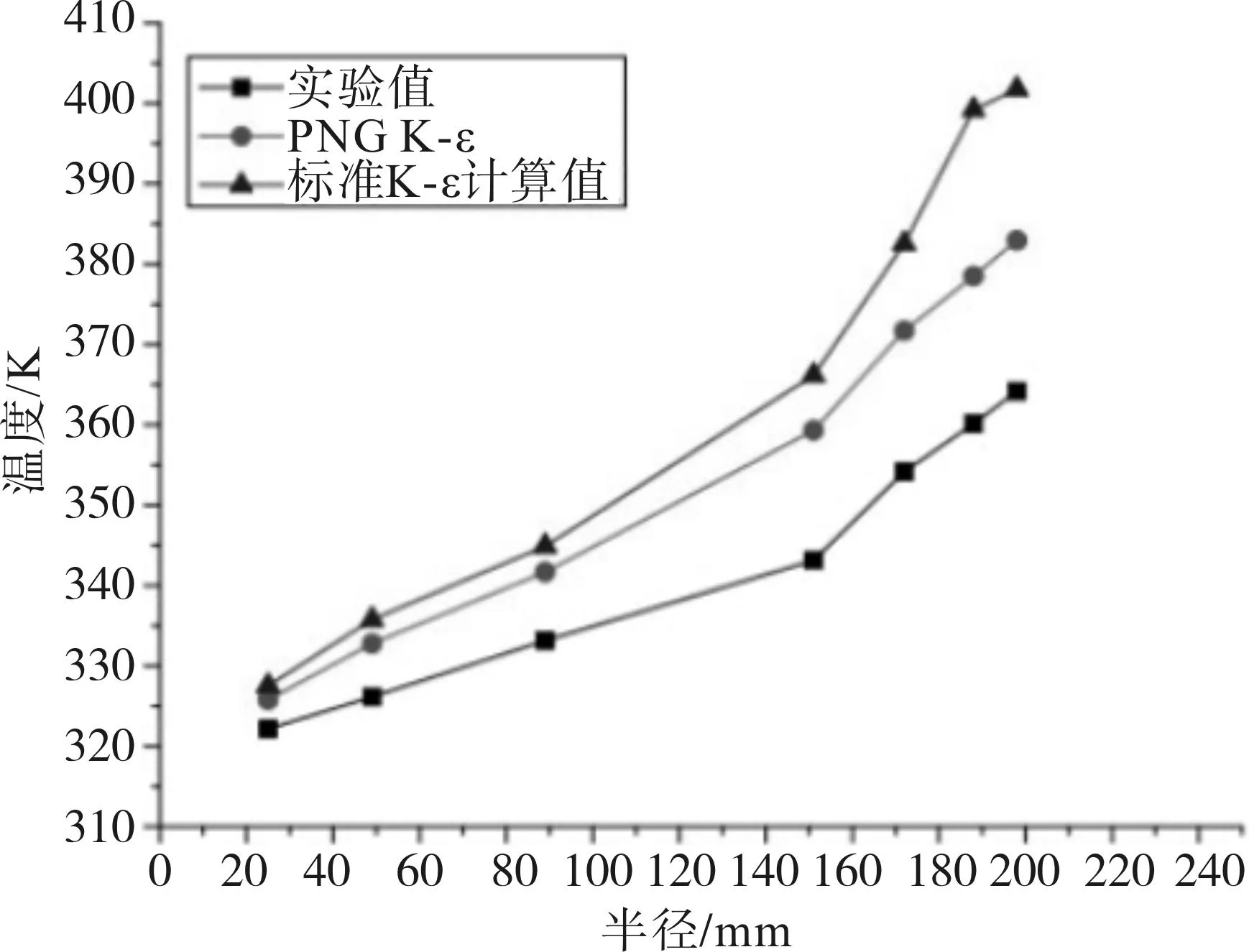
图2　上游盘数值计算值与实验值对比

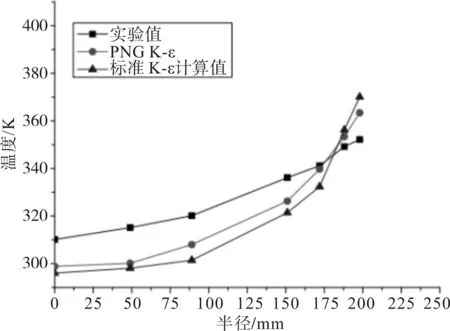
图3　下游盘数值计算值与实验值对比

由图2和图3可知，采用标准k-ε湍流模型得到的计算值和采用RNG k-ε湍流模型得到的计算值与实验值相比较，RNG k-ε湍流模型计算值更接近于实验值，因此本文采用RNG k-ε湍流模型作为数值计算的湍流模型。由于采用RNG k-ε湍流模型的计算值与实验值的误差在工程允许范围内，从而验证了本文所选用的数值计算方法的正确性。

2计算结果及分析

两个对转盘壁面与盘腔内冷却空气流的摩擦力矩定义为公式(2)：

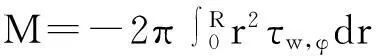
(2)

其中，对上游盘，τw,φ=μ(∂υφ/∂z)z=0，对下游盘，τw,φ=μ(∂υφ/∂z)z=H。

定义上游盘与下游盘的转速比为τ，其范围为τ<0。由于两盘转速比范围为τ<0，两盘反向旋转，根据公式(2)可知两盘壁面摩擦力矩相反，如图4～8所示。

本文建立了四个盘腔间距H为23mm，38mm，53mm，83mm的计算模型。分别计算了这四种盘腔间距在上游盘转速+1000rpm，下游盘转速-1000rpm，中心进气量l为200kg/h，室温295K的工况条件下的结果。图4给出了壁面摩擦力矩随盘腔间距的变化图。

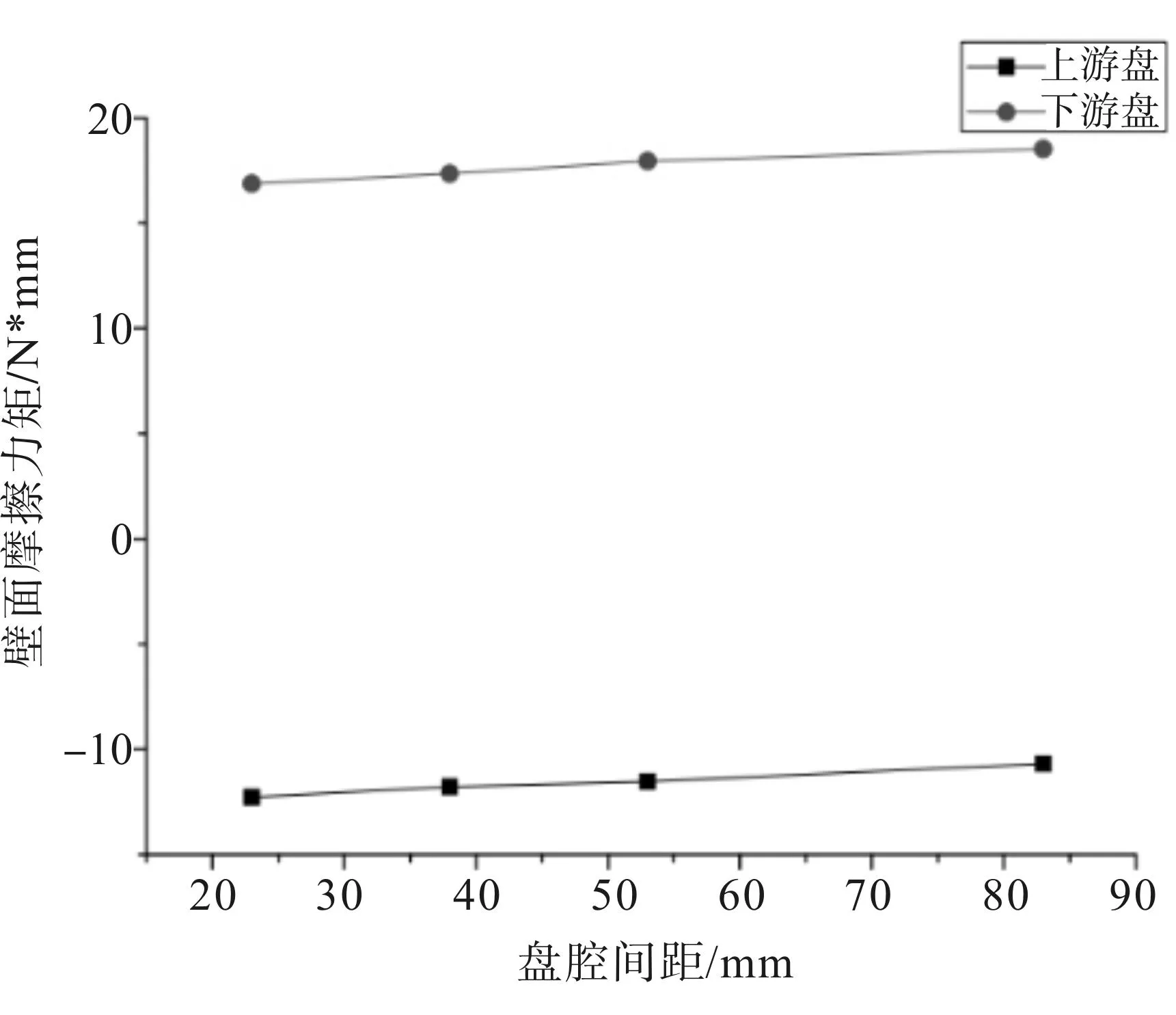
图4　壁面摩擦力矩随盘腔间距的变化

如图4所示，两盘壁面摩擦力矩随盘腔间距的变化不明显，这是由于冷却空气以相同的进气量进入盘腔，在实验盘腔间距取值范围内，盘腔间距的变化对腔内气流的流动速度影响不明显，且两盘转速不变，故所对应的切向速度梯度变化不大，根据公式(2)，故两盘壁面摩擦力矩随盘腔间距的变化不明显。

2.2中心进气流量的变化对上下游盘壁面摩擦力矩的影响

在盘腔间距53mm，上游盘转速+1000rpm，下游盘转速-1000rpm，室温295K的工况条件下，对中心进气流量l为：100kg/h，200kg/h，300kg/h，400kg/h，500kg/h分别进行了数值模拟计算。图5为壁面摩擦力矩随中心进气流量的变化图。

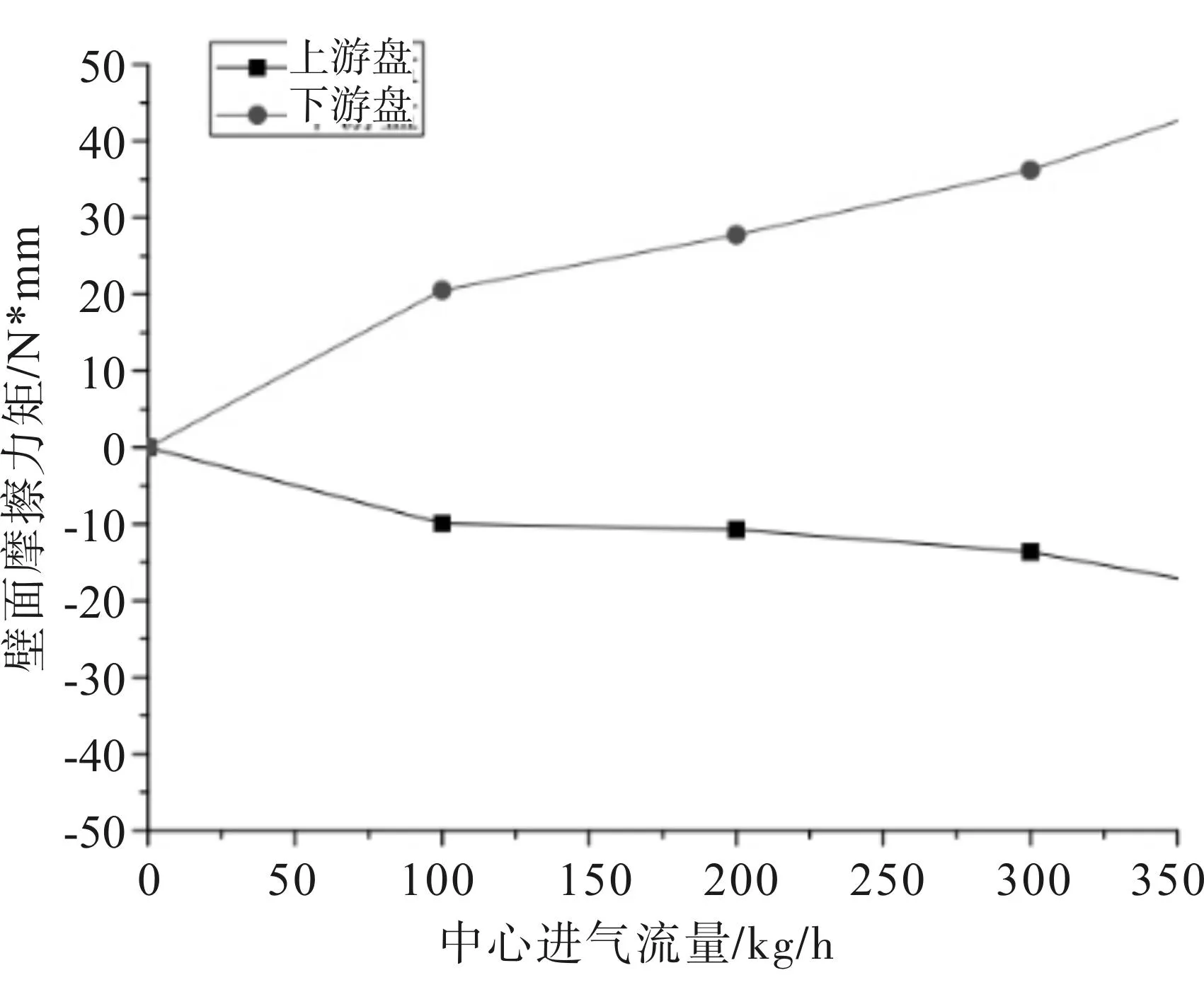
图5　壁面摩擦力矩随中心进气流量的变化

如图5所示，两盘壁面摩擦力矩随流量的增大而增大，这是由于冷却空气流量的增大，使盘腔内气流的流动速度增大，其所对应的切向速度梯度也增大，根据公式(2)，故摩擦力矩也增大。

2.3上下游盘转速的变化对上下游盘壁面摩擦力矩的影响

计算工况为盘腔间距53mm，中心进气流量l为200kg/h，上游盘为正转速，下游盘为负转速，室温295K。

(1)根据上文提到两盘转速比的范围，当转速比τ为-1不变时，上游盘和下游盘转速的变化对两盘壁面摩擦力矩的影响，如图6所示。

如图6所示，两盘壁面摩擦力矩随两盘转速的增大而增大，这是由于两转盘转速的增大，使其所对应的切向速度梯度也增大，根据公式(2)，故两盘壁面的摩擦力矩随之增大。

图6　壁面摩擦力矩随转速的变化1

(2)根据上文提到两盘转速比的范围，当转速比τ<-1，下游盘转速保持-1000rpm不变时，转速比τ的变化对两盘壁面摩擦力矩的影响，如图7所示。

如图7所示，当转速比τ<-1，下游盘转速不变时，上游盘摩擦力矩随转速比的增大而减小，这是由于下游盘转速不变，转速比τ从-3增大到-1，使上游盘转速的绝对值减小，上游盘所对应的切向速度梯度也减小，而下游盘转速不变，下游盘所对应的切向速度梯度也不变，根据公式(2)，故上游盘壁面摩擦力矩随之减小，而下游盘壁面摩擦力矩不变。

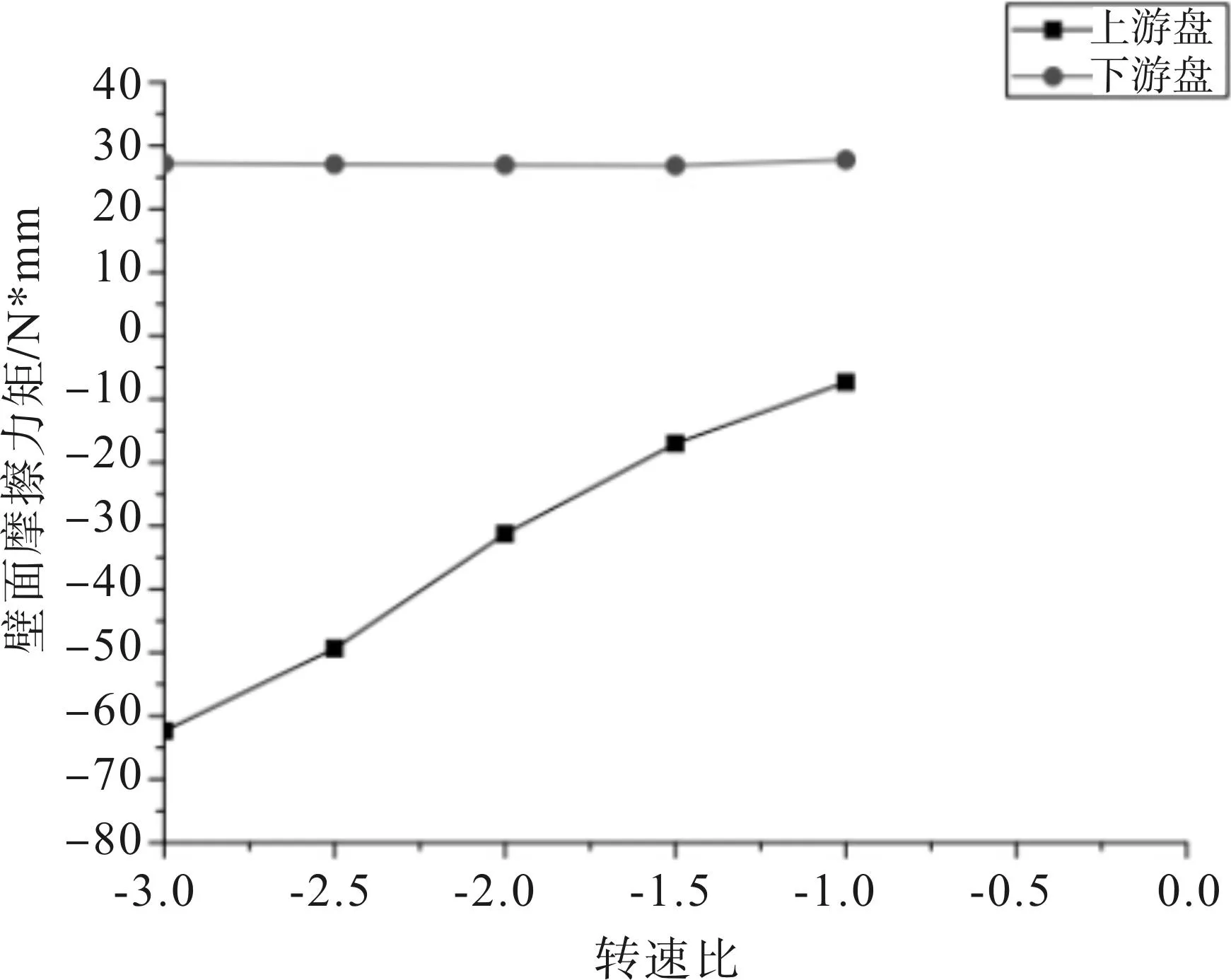
图7　壁面摩擦力矩随转速的变化2

(3)根据上文提到两盘转速比的范围，当转速比-1<τ<0，上游盘转速保持+1000rpm不变时，转速比τ的变化对两盘壁面摩擦力矩的影响，如图8所示。

如图8所示，当转速比-1<τ<0，上游盘转速不变时，下游盘摩擦力矩随转速比的增大而增大，这是由于上游盘转速不变，转速比τ从-1增大到0，使下游盘转速的绝对值增大，下游盘所对应的切向速度梯度也增大，而上游盘转速不变，上游盘所对应的切向速度梯度也不变，根据公式(2)，故下游盘壁面摩擦力矩随之增大，而上游盘壁面摩擦力矩不变。

图8　壁面摩擦力矩随转速的变化3

3结语

在上述对转盘腔模型的模拟计算中，得到以下结论。

(1)盘腔间距在实验范围(23～83mm)内，两盘壁面摩擦力矩随盘腔间距的变化不明显；当中心进气流量从100kg/h增大到500kg/h时，两盘壁面摩擦力矩都会随着中心进气流量的增大而增大，中心进气流量越大，两盘壁面摩擦力矩越大。

(2)在上游盘与下游盘转速比为-1时，两盘壁面摩擦力矩随着两盘转速的增大而增大，转速越大，两盘壁面摩擦力矩越大；而当上游盘转速不变，下游盘转速增大，其上游盘与下游盘转速比为-1<τ<0时，上游盘壁面摩擦力矩不变，而下游盘壁面摩擦力矩会随转速比的增大而增大；当下游盘转速不变，上游盘转速增大，其上游盘与下游盘转速比为τ<-1时，下游盘壁面摩擦力矩不变，而上游盘壁面摩擦力矩会随转速比的增大而减小。

参考文献

[1] 陈大光.燃气涡轮推进技术的未来发展[J].燃气涡轮实验与研究,1997,10(3):1-8.

[2] 季路成.对转涡轮研究的回顾与展望[J].航空发动机，2006,32(4):49-53.

[3] 梁春华.通用的经济可承受的先进涡轮发动机研究计划的主要特点[J].航空发动机,2011,37(5):58-62.

[4] Gan X,Kilic M,Owen J M.Flow between contrarotating disks [J].Journal of Turbomachinery,1995,117(2): 298-305.

[5] Chen J X,Gan X,Owen J M.Heat transfer from air-cooled contrarotating disks[J].Journal of Turbomachinery,1997,119(1):61-67.

[6] 蔡毅,徐国强,陶智,等.反向旋转盘间非稳态换热特性的实验研究[J].航空动力学报,2004,19(3):346-350.

[7] 陈淑仙,张靖周,谭晓茗,等.反向旋转盘腔内部流动特性[J].航空动力学报,2013,28(1):136-142.

[8] 陶文铨.数值传热学[M].西安:西安交通大学出版社,1998:125-132.

[责任编辑、校对：梁春燕]

Effects of Counter-rotating Turbine Cavity Parameters on Friction Moment of Rotating Disk Wall

SHIXue-jie,CHENShu-xian,LIANGZhen-yu

(Aviation Engineering Institute,Civil Aviation Flight University of China,Guanghan 618307,China)

Abstract：The friction moment in counter-rotating disk cavity will directly affect the gas flow structure and heat transfer efficiency which in turn has an effect on the counter-rotating turbine engine properties.In this paper,numerical simulation of gas flowing in counter-rotating disk cavity was carried out by RNG k-ε turbulence model to research the impact of counter-rotating turbine disk cavity separation distance,central air intake rate,and the changes of disk rotary speed on friction moment of the rotating disk wall.The result of simulation shows that friction moment on the rotating disk wall does not obviously change with disk cavity separation distance within computing scope while increasing with the increases of central air intake rate and rotating speed.

Key words：counter-rotating disk cavity;numerical simulation;turbulence model;friction moment

收稿日期：2016-03-01

基金项目：国家自然科学基金(51306201)；江苏省航空动力系统实验室开放课题(APS-2013-04)；中国民用航空飞行学院研究生创新项目(X2014-11)

作者简介：史学捷(1987-)，男，山西阳泉人，硕士研究生，主要从事航空发动机流动传热特性研究。

中图分类号：V231.1

文献标识码：A

文章编号：1008-9233(2016)03-0012-05