城市道路交通与居住地选择的模糊多目标规划模型

刘　睿，李　华，张惠玲

(西安航空学院 理学院，陕西 西安 710077)

城市道路交通与居住地选择的模糊多目标规划模型

刘睿，李华，张惠玲

(西安航空学院 理学院，陕西 西安 710077)

摘要：首先建立了以家庭月生活成本不高于月收入和基本不高于预算等为约束，以基本实现家庭月交通时间最小、月生活成本最小和小区周边居住环境最优为目标的模糊多目标模型，其次，引入Z-隶属度函数来描述模糊数据，并将模糊多目标模型转换为单目标线性规划模型。最后, 通过改变城市道路交通状况得到了小区入住率的变化, 从而获得了城市交通与居住地选择之间的内在联系。

关键词：模糊多目标规划；月交通时间；Z-隶属度函数

0引言

随着我国经济的持续快速发展，城市化进程的加速，城市机动化水平日益提高，道路交通量迅猛增长，随之产生了一系列的交通问题，其中最为严重的就是城市交通拥堵[1]。从2000年到2009年，中国城镇化率由36.2%提高到46.6%，年均提高约1.2个百分点。城镇人口由4.6亿增加到6.2亿，净增1.6亿人。城镇县城区面积由2000年的2.24万平方公里增加到2008年的3.63万平方公里，增加了62%。截至2008年末，我国共有建制城市655座，其中百万人口以上的特大城市122座，城市市辖区地区生产总值占到当年全国GDP的62.7%。

当前交通与居住地选择之间的模型的主要研究方法为数学规划模型及Logit模型。数学规划模型旨在于寻找家庭的最优居住地，强调了交通与土地利用的一体化。Bravo建立了土地利用和交通之间相互作用的静态均衡的数学规划模型[2]，Pinjiari的模型中考虑了家庭住宅类型、小汽车拥有量、通勤方式等因素寻找最合适的居住地[3]。Logit模型中，应用最广的为Multinomial Logit模型，但因为其无法刻画备选方案之间的关联性，会导致决策失误[4]，随之Nested Logit模型克服了上述缺点，但其仅考虑一维关联性，具有一定局限[5]。

鉴于国内外研究现状，本文建立了模糊多目标优化模型，能够更加准确地模拟居民选择居住地的实际情况，其次使用隶属度函数将模糊多目标规划转化为确定的多目标规划，再将多目标规划转化为单目标规划并予以求解，最后进行算例分析。

1居住地选择模型

本文将城市中的所有道路按照交叉口分割为路段，且每个路段末端均设有交通信号灯与公交车站。O={Om}，m=1,2,3,…为居住地集合，D={Dn},n=1,2,3,…为目的地集合。A={Ai},i=1,2,3,…为更改居住地的家庭集合，A=F1∪F2∪F3且F1∩F2∩F3=Ø，其中，F1为高收入家庭的集合，F2为中等收入家庭的集合，F3为低收入家庭的集合。

1.1家庭月交通时间

国内城市的通勤方式大多为步行、自行车、电动车(包含摩托车)、公交车、自驾(包含打车)与搭顺车六种。以上六种出行方式的指标参数依次定义为δji(i=1,2,…,6)，速度依次为vi(i=1,2,…,6)。

其中，aj∈Ai∈A为家庭成员。

本文假设高收入家庭拥有两辆汽车，中等收入家庭拥有一辆汽车，低收入家庭不拥有小汽车。

在交通高峰期，公交车、自驾与搭顺车出行在同一路段上的平均速度是相同的，均由道路长度及其车流量决定，故在路段a上，v3=v4=v5=va(fa)，va(fa)为路段a的当流量为fa时的车流速度。τa表示车辆经过路段a末端交叉口的时间，公交车有等车时间与车辆进出站时间。因此家庭月交通时间T可描述为：

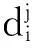
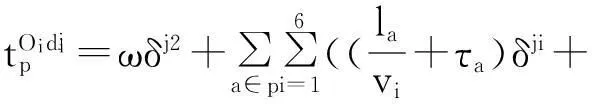
1.2家庭月生活成本

每个家庭的月生活成本由月平均房屋购置费mr，月物业管理费mh，月家庭生活费mm，月交通费用mt构成，即M=mr+mh+mm+mt。

mr为月平均房屋购置费或租房费用，本文不予以区分，均按购房对待。假设首付为家庭已有财产，剩余房款按最长年限按揭贷款，则每月还款金额为月平均房屋购置费。mh为月物业管理费，由房屋面积、房屋楼层、居住地位置、单位房价不同而发生变化。mm为月家庭生活成本费，由家庭成员的人数、居住地附近的物价水平、该城市物价水平以及家庭可支配收入决定。本文按照最低平均人均可支配收入来计算。

月交通费用mt：

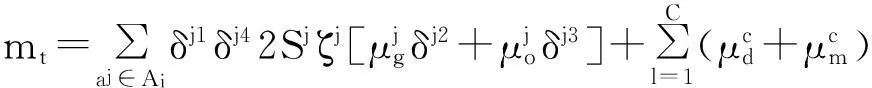
1.3居住地周边环境

用Z表示居住地周边环境。居住环境是一个综合因素，对于选择居住地的家庭来说，比较关心居住地附近是否有幼儿园、小学、菜市场、医院、公园及大型购物中心等配套设施。

本文考虑在居住地1000m内，拥有上述配套设施的数目。令Z=0，对该居住地周边1000米内是否拥有上述六种配套设施依次判定，若有，则Z+1；否则，Z+0。

1.4模型建立

当家庭选择其居住地时，希望能够同时实现交通时间最短、生活成本最小及居住地周边环境最好。但这些参数不是一成不变的，故其模型为模糊多目标优化模型：

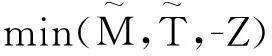
(1)

2模型求解

2.1Z-隶属度函数

Z-隶属度函数如图1所示:

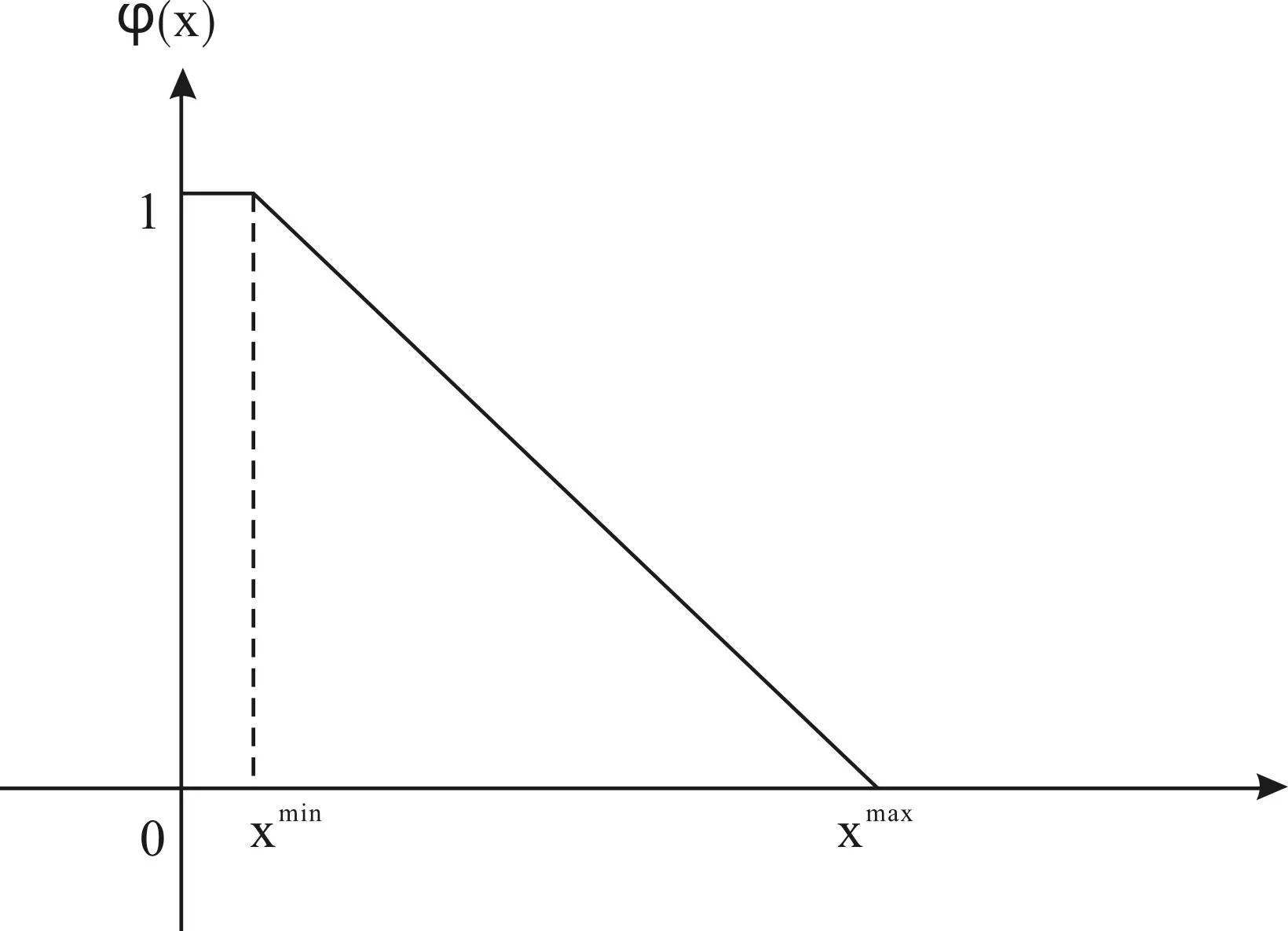
图1　Z-隶属度函数

(2)

2.2模型转换

对于家庭Ai∈Fε,ε=1,2,3依次代表高、中、低收入家庭。其居住地选择模型为模糊多目标优化模型(1)，定义其中每个模糊参数的Z-隶属度函数如下:

(3)

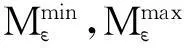
(4)

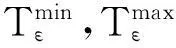
(5)

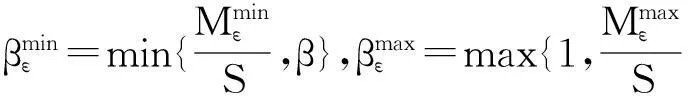
可将模糊多目标优化模型(1)转换为:

(6)

3算法设计

家庭选择居住地的模型算法如下：

(1)置各条道路的流量fa=0，得到va(fa)；

(2)随机获得一个准备更改居住地的家庭Ai，根据其家庭收入，得到Ai∈Fε，及Ai的目的地Dn；

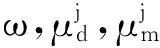
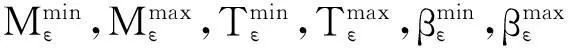
(5)根据lingo软件对模型(6)求解, 得到Ai的居住地选择居住地Om，且得到Om↔Dn的最短交通时间路线p，若a∈p，则fa=fa+1，得到va(fa)；

(6)令A=A-{Ai}。如果A=Ø，结束；否则，返回步骤(2)。

4算例

4.1问题描述

由文献[6]可得如下算例，如图2所示，把一个小型城市分成九个居住地(1-9)，三个主要目的地A、B、5。

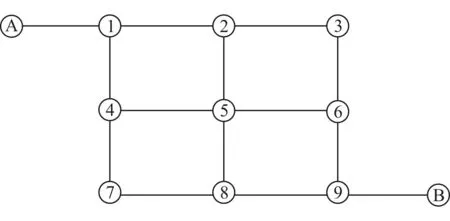
图2　城市规划图

城市各道路长度、容量和自由流速度如表1所示。每个居住地平均房价，居住地周边配套设施数目如表2所示。

现假设每个居住地有20%的家庭准备更改居住地，且其高、中、低收入家庭各个目的地是均匀分布的。道路流量/容量和平均速度/自由流速度之间数值对应关系如表3所示。

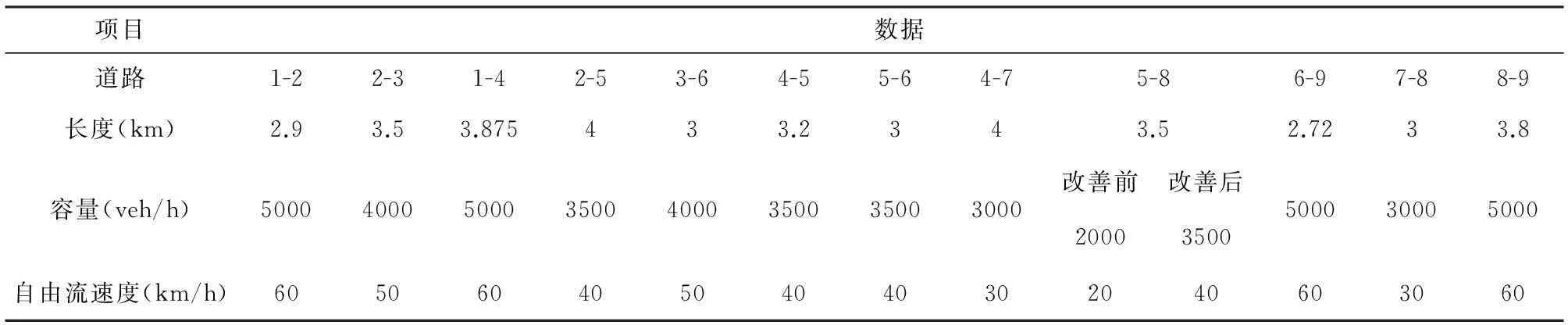
表1　简单交通路网(交通状况改善前后)的静态属性

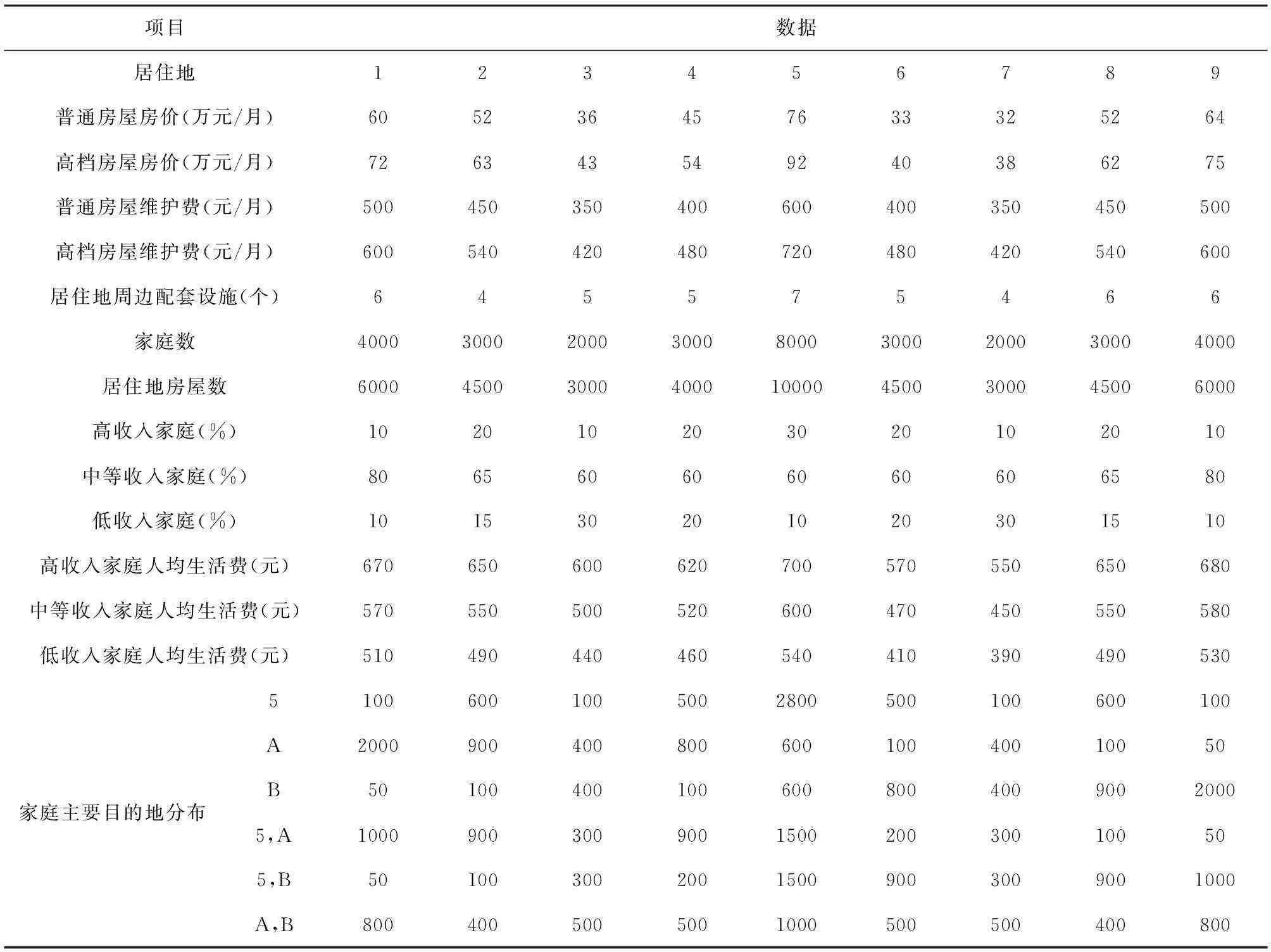
表2　各居住地的静态数据

表3　道路平均速度与流量对照表

4.2参数取值

下面给出模型中使用到的各个参数取值。

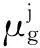
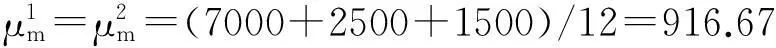
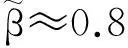
本文按照本额等息的还款方式计算月供，且假设首付为房屋总价的30%，贷款时间为30年，打折后的银行贷款利率为3.96%，购买房屋的月还款金额计算公式为：

则计算可得购房家庭的月还款金额见表4。

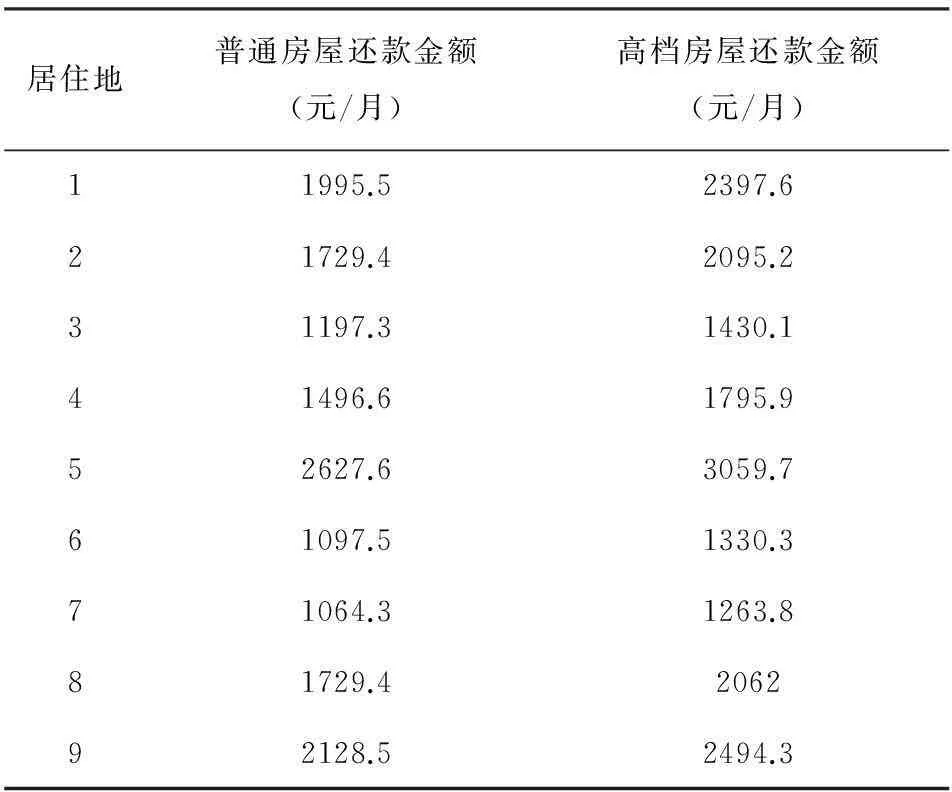
表4　月还款金额表

4.3算例分析

代入4.2中所有数据，用算法1求解4.1中的算例。

本文做了两组实验数据。

第一组：当道路5-8未改善时，计算准备更改居住地的家庭对居住地的选择结果与各居住区的入住率(见表5、表6)。第二组：当道路5-8改善后，其他条件如同第一组不变，计算第一组中改变居住地的家庭对居住地的重新选择结果与各个居住地的入住率(见表7、表8)。并将两组试验的结果进行比较(见表9)。

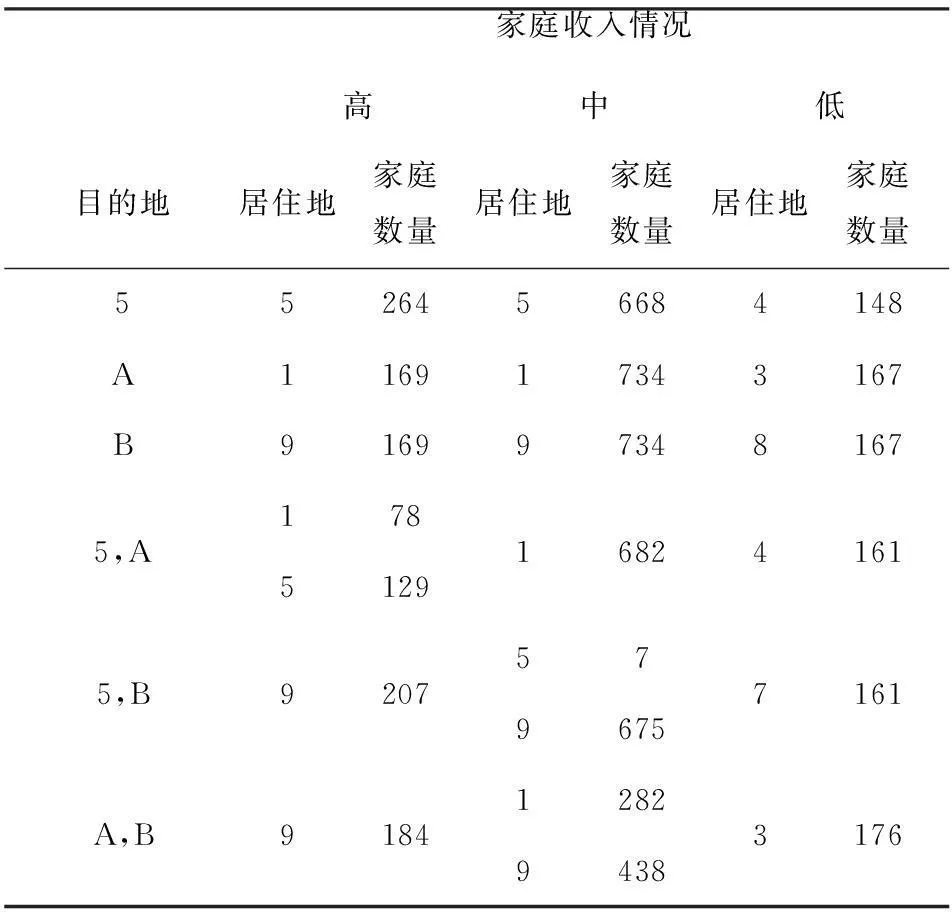
表5　道路5-8改善前更改居住地的家庭选择情况

由表5可知，改善道路5-8前，希望更改居住地的家庭中高收入与中等收入家庭都偏向选择距离目的地较近且居住地周边环境较好的1、5、9，低收入家庭偏向选择3、4、7、8。由表7可知，改善道路5-8后，希望更改居住地的家庭中高收入的选择没有变化，中等收入家庭中目的地为5, B的家庭有一部分放弃9改而选择环境更好的5，其他不变。低收入家庭的影响较大，原来选择4的家庭近一半转向8，原选择3的家庭也有一半转向选择4，原选择7的家庭全部转向选择6。

表6　道路5-8改善前居住地居住情况

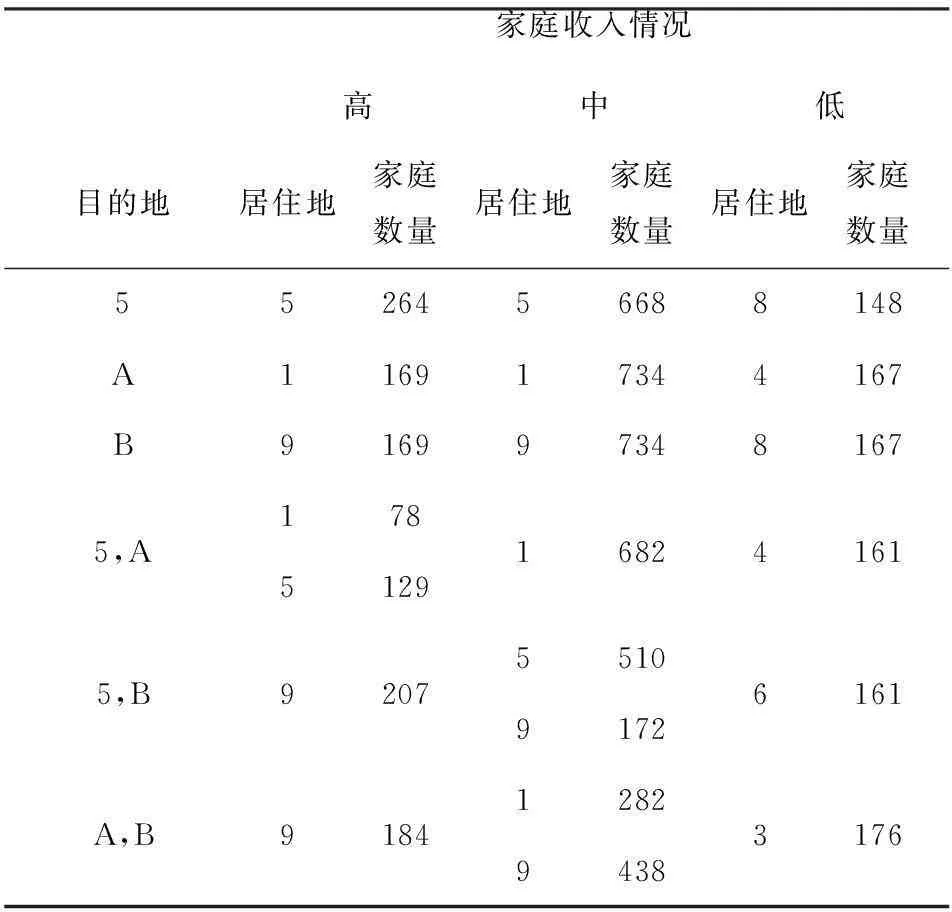
表7　道路5-8改善后更改居住地的家庭选择情况

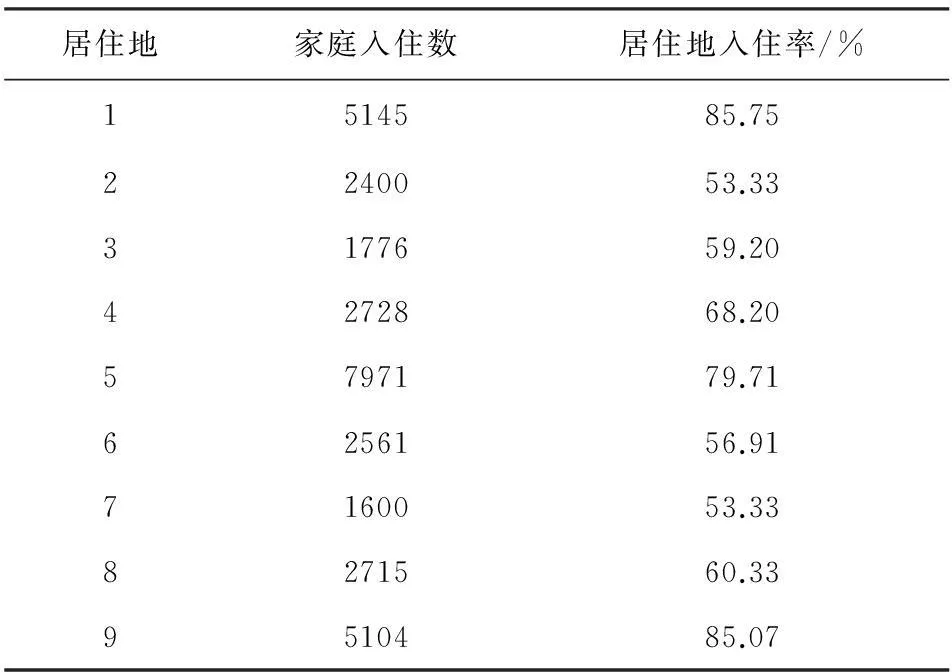
表8　道路5-8改善后居住地居住情况

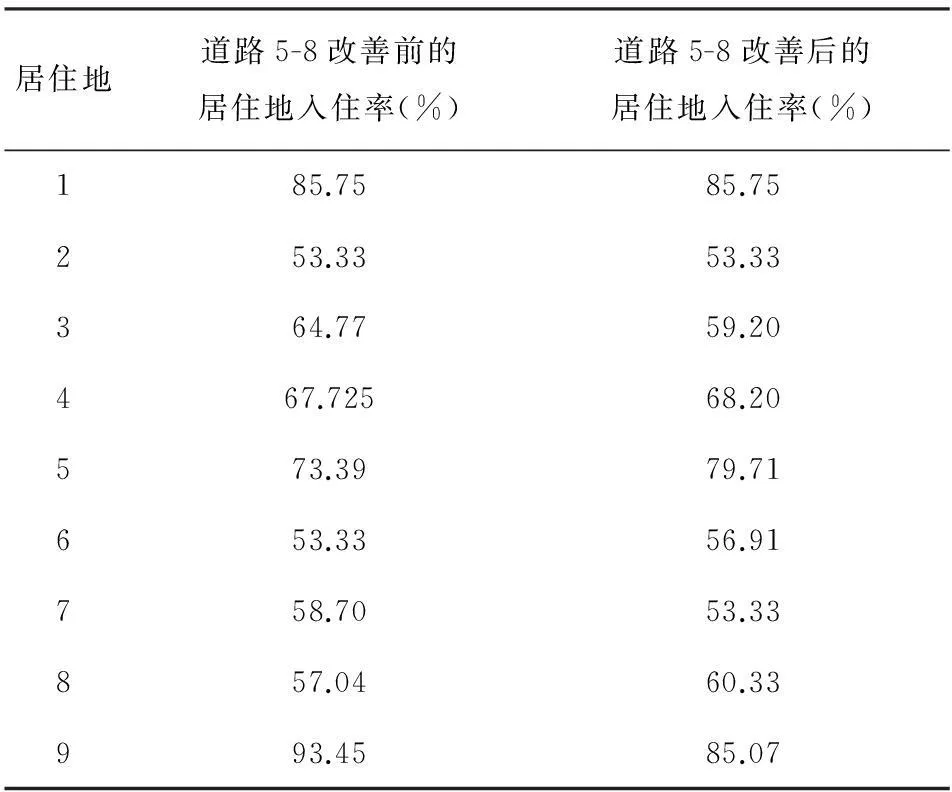
表9　道路5-8改善前后居住地入住率的变化

由表9可知，由于道路5-8改善，使得3、7、9的入住率减少，5、6、8的入住率显著增大，4的入住率略有增加，从而优化了1、3-9八个居住地之间的交通和空间结构。

综上所述，一方面，改善道路对高收入家庭几乎不产生影响，对中等收入家庭影响较小，主要对低收入家庭产生影响；另一方面，入住率有显著增加的三个居住地有两个都位于改善道路的沿线，即改善某条道路交通后，有助于提高该条道路沿线的居住地入住率。

参考文献

[1] 毛蒋兴，阎小培.我国城市交通系统与土地利用互动关系研究述评[J].城市规划汇刊，2002(4):34-37，79.

[2] Bravo M,Briceno L,Cominetti R,et al.An Integrated Behavioral Model of the Land-use and Transport Systems with Network Congestion and Location Externalities[J].Transportation Research Part B:Methodological,2010,44(4):584-596.

[3] Pinjari A R,Bhat C R,Hensher D A.Residential Self-selection Effects in an Activity Time-use Behavior Model[J].Transportation Research Part B:Methodological,2015,43(7):729-748.

[4] Bhat C R,Guo J Y.A Mixed Spatially Correlated Logit Model:Formulation and Application to Residential Choice Modeling[J].Transportation Research Part B:Methodological,2004,38(2):147-168.

[5] 杨励雅，李霞，邵春福.居住地、出行方式与出发时间联合选择的交叉巢式Logit模型[J].同济大学学报(自然科学版)，2012,40(11):1647-1653.

[6] 王媛媛，陆化普.基于可持续发展的土地利用与交通结构组合模型.清华大学学报(自然科学版),2004,44(9):1240-1243.

[7] 张邻,杜文,郭倩倩.城市居住地与交通系统关系的谈判机制模型[J].交通运输工程学报,2010,10(6):102-110.

[责任编辑、校对：李琳]

The Fuzzy Multi-objective Optimization Model for the Relationship between Urban Transport and Residential Occupancy Choice

LIURui,LIHua,ZHANGHui-ling

(School of Science,Xi′an Aeronautical University,Xi′an 710077,China)

Abstract：Fuzzy multi-objective optimization model is proposed,and the objective functions are:probably to realize to minimize the family monthly transportation time and living-cost,and to maximize the completeness of the residential quarters surrounding infrastructures.Then,the fuzzy data is described by Z-shape membership function,and the fuzzy multi-objective optimization model is transferred to single-objective linear optimization model.Finally,the new residential occupancy probably rate can be obtained by changing the traffic conditions,and thus presenting the relationship between urban transport and residential occupancy choice.

Key words：fuzzy multi-objective optimization model;monthly transportation time;Z-shape membership function

收稿日期：2016-04-18

基金项目：西安航空学院校级高等教育研究项目(2016GJ1004)

作者简介：刘睿(1984-)，女，陕西西安人，博士，讲师，主要从事数学建模方面的研究。

中图分类号：U491

文献标识码：A

文章编号：1008-9233(2016)03-0070-06