一种可变形跨介质航行器气动/水动特性分析

廖保全, 冯金富, 齐铎, 李永利, 余宗金

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

一种可变形跨介质航行器气动/水动特性分析

廖保全, 冯金富, 齐铎, 李永利, 余宗金

(空军工程大学 航空航天工程学院, 陕西 西安 710038)

摘要:由于海水和空气物理性质存在巨大差异,航行器很难以单一外形满足在两种环境下的航行要求。为此,提出一种通过改变外形来实现水空介质跨越的航行器,并通过计算流体力学对其空中和水中两种外形的气动/水动特性进行研究。仿真结果表明,通过改变外形,航行器能够同时满足水下航行和空中飞行的要求。水下航行时,航行器在较小的仰角范围内通过收缩机翼减小阻力;空中飞行时,通过展开机翼增大升力。

关键词:计算流体力学; 气动特性; 水动特性

0引言

随着航空航海技术的发展和军事需求的推动,以隐蔽性好、突防能力强为优势的跨介质航行器获得了广泛关注[1]。跨介质航行器是指能够多次跨越介质且能持续航行、重复使用的航行器。2008年,美国国防先进技术研究局着手研制一种既能够在空中飞行,又能够在水面和水下航行的新概念飞机[2]。与此同时,美国军方研制中的另一款水下发射无人飞机“鸬鹚”(Cormorant)已取得实质进展。法国波尔多航空技术公司正研制将用于海洋研究、港口和海岸警戒的潜水飞机“埃利乌斯”(Aelius)。

研究和实践均表明,水面舰艇的防空体系和水下防御系统仅对空和反鱼雷来说存在诸多优势。美国自1944年发展舰空导弹以来,先后发展装备了7大系列11种舰艇防空武器,出现了标准系列、海麻雀系列、拉姆系列、宙斯盾防空系统等性能优越的防空武器[3]。在反鱼雷方面,美国提出的潜艇和水面舰艇的水声对抗系统(SAWS)、法国的“信天翁”(Albatros)鱼雷预警系统、意大利C300和C303鱼雷防卫系统等大大降低了鱼雷的生存概率和攻击性。因此,设计一种能够利用水空介质物理割裂,通过在水空介质间跳跃飞行(航行),实现远距离隐蔽侦察、打击的航行器具有重要意义。

本文提出一种通过改变外形实现水空介质跨越的航行器,兼顾空中突防速度快和水中突防隐蔽性好的特点:在水中航行时,采用类似鱼雷的外形;在空中飞行时,采用类似反舰巡航导弹的外形。通过试验获取航行器动力特性参数,试验准备周期长、耗费大;而文献[4-5]采用数值模拟方法,通过Ansys ICEM对所建立的模型进行网格划分,借助Fluent软件获得较准确的动力特性数据。本文通过数值模拟研究所提出的航行器外形的动力学特性,以期对跨介质航行器的外形设计和试验研究提供参考。

1几何模型

从现有航空飞行器与水下航行器外形来看,两者存在巨大差异,造成其差异的根源在于水和空气两种流体物理性质的不同。海水的密度是空气密度的833倍,其动力粘性系数是空气的60倍。根据雷诺数相似原理,外形不变的航行器在相同速度下,水下航行产生的升力是空中飞行产生升力的14倍。这使得航行器在空中飞行必须保持高速度,而在水中航行必须保持低速和较大的负迎角。较大的速度变化对发动机提出了很高的要求,负迎角产生的诱导阻力和弹翼本身的粘性阻力、压差阻力使得弹翼不利于水中航行。

本文提出一种通过向上两次折叠弹翼改变外形的跨介质航行器。航行器长度为6 m,径向截面外接圆直径0.534 m,便于从现有鱼雷发射管发射。航行器翼展为1.42 m,弹翼收起时折叠于弹身两侧的弹翼槽内,呈类鱼雷外形。航行器密度为1 100 kg/m3,质量为910 kg。根据以上参数,建立了航行器的几何模型,如图1所示。

图1　航行器几何外形Fig.1　Geometric shape of the vehicle

2网格划分

网格是计算域内的一系列离散点。通过将控制方程离散,使用数值方法得到网格节点上的数据(如速度、温度、压力等),即得到数值解[6]。网格可以分为结构化网格和非结构化网格。结构化网格便于调整网格疏密和边界层处理,网格生成速度快,数据结构简单。但对于复杂几何体而言结构化网格生成工作量大,对外形适应性差。本文所提出的航行器空中模型、水中模型均比较复杂,因此采用非结构化网格方法。该方法能够离散复杂外形区域,可以在计算域精确表示物理边界,保证了边界处的初始准确度,提高了解的质量;但非结构化网格生成过程计算机工作量大,对计算机性能要求高。使用曙光A840r-G计算机群能够满足非结构化网格对计算性能的要求,能够顺利地生成网格,如图2所示。

图2　航行器的网格Fig.2　Mesh generation of the vehicle

为了减少计算域边界对结果的影响,计算域确定为远大于几何模型的55 m×10 m×10 m长方体,航行器头部距计算域入口20 m。壳网格的网格类型为All Tri,即生成所有网格单元均为三角形。网格生成的计算法则选用Patch Dependent,根据面的轮廓线生成网格,这样能够更好地捕捉几何特征。在生成网格时对航行器头部、尾部和弹翼等外形变化大的部位的曲线进行加密。壳网格生成后,经检查网格质量符合要求,再生成体网格。弹翼、尾翼后缘附近流场参数变化剧烈,对气动、水动特性影响较大。生成体网格时,对弹翼、尾翼后缘附近计算区域进行了加密。最后,通过对生成体网格的检查、修改,得到质量较好的网格。空中飞行状态模型的网格数量为600多万,水中航行状态模型的网格数量为500多万。

3数值方法与边界条件

航行器在流体中航行时,涉及到复杂的湍流问题。一般认为无论多么复杂的湍流运动,都可以通过求解Navier-Stokes方程和连续性方程解决。由于湍流运动的复杂性,人们通过一些数值方法对湍流进行模拟并取得了较好的效果。湍流数值模拟的方法主要有直接数值模拟(DNS)和非直接数值模拟。直接模拟方法计算量大,对计算机性能要求高,难以在工程应用中推广。在实际应用中,使用最多的数值模拟方法是Reynolds平均法,通过引入湍流模型封闭方程组求解湍流要素的时均值[7]。

3.1通用控制方程

对于流体的控制方程主要有连续性方程、动量方程(又称Navier-Stokes方程)、能量守恒方程等。可以写出其通用形式[8]:

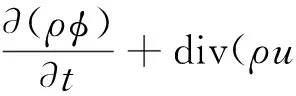
(1)

式中:φ为通用变量;Γ为广义扩散系数;S为广义源项。

当φ=1,Γ=0,S=0时,方程为连续性方程;当φ=ui,Γ=μ,S=-∂p/∂xi+Si时,方程为动量方程。

3.2湍流模型

基于SST(Shear Stress Transport)模型的k-ω方程考虑了湍流剪切应力的传输,可以很好地处理近壁面处低雷诺数的数值计算,并且综合了k-ω模型在远场计算的优点,处理不同界面具有较好的适应性,收敛效果更好。k-ω模型主要求解湍动能k和湍流频率ω两个运输方程:

(2)

(3)

式中:Pk为由层流产生的湍流动能;σk,σω分别为k和ω方程的湍流能量普朗特数。

采用Fluent中的默认值:α=0.52,β′=0.09,β=0.072,σk=2,σω=2。湍流黏度μt与湍流动能和湍流频率有关,其关系式为:

(4)

3.3边界条件

计算域为55 m×10 m×10 m的长方体,流体入口距航行器顶端20 m,流体出口距航行器顶端35 m。对空中飞行特性仿真研究时,选择基于密度的隐式求解器,计算域内介质为空气。设定与空气有关的物理参数,部分参数采用默认值。流体入口的边界类型为Pressure-far-field,假定航行器掠海飞行,距海面高度50～150 m(战斧导弹巡航马赫数为0.72,巡航高度为50～150 m),表压设定为101.33 kPa,马赫数为0.72。选择笛卡尔坐标系速度分量定义方式,速度分量随航行器迎角α的变化而变化。对外流场的计算选择intensity and length scale湍流组合,湍流强度定义为速度脉动的均方根与平均速度的比值:

(5)

湍流尺度通常用下式估算:

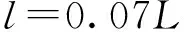
(6)

航行器壁面为无滑移壁面,采用亚松弛因子默认值计算初场。为了加速收敛,在计算过程中作了适当放大,同时采用二阶迎风格式,能得到更加精确的结果。

对水中航行特性进行研究时,选择基于压力的隐式求解器,计算域介质为海水。流体入口边界类型为Velocity-inlet。假定航行器航行深度为5 m,表压设定为151.54 kPa。选择笛卡尔坐标系速度分量定义方式,合速度大小为20 m/s,速度分量随航行器迎角α的变化而变化。

4仿真验证及结果分析

在进行航行器流体仿真之前,通过对MK46鱼雷的流体仿真研究了本文方法对水中航行器仿真的准确性,得到其在迎角为0°、速度为20 m/s状态下,阻力系数为0.097 2,与潘光等[9]的仿真结果相近,与试验值[10]的误差在可接受范围。通过对M6翼型流体仿真研究了本文方法对空中航行器仿真的准确性,所得压力系数的分布情况与试验结果吻合较好。

本文仿真了航行器水中模型在航行速度分别为16 m/s,20 m/s和24 m/s,迎角由-45°变化到45°共93种工况的流场;仿真了航行器空中模型分别在Ma=0.62,0.72,0.82飞行速度下,迎角变化范围为-45°～45°共93种工况。

图3展示了Ma=0.72的空中飞行速度在0°迎角时的升力系数及阻力系数的收敛情况,在进行到600步时,系数趋于稳定。

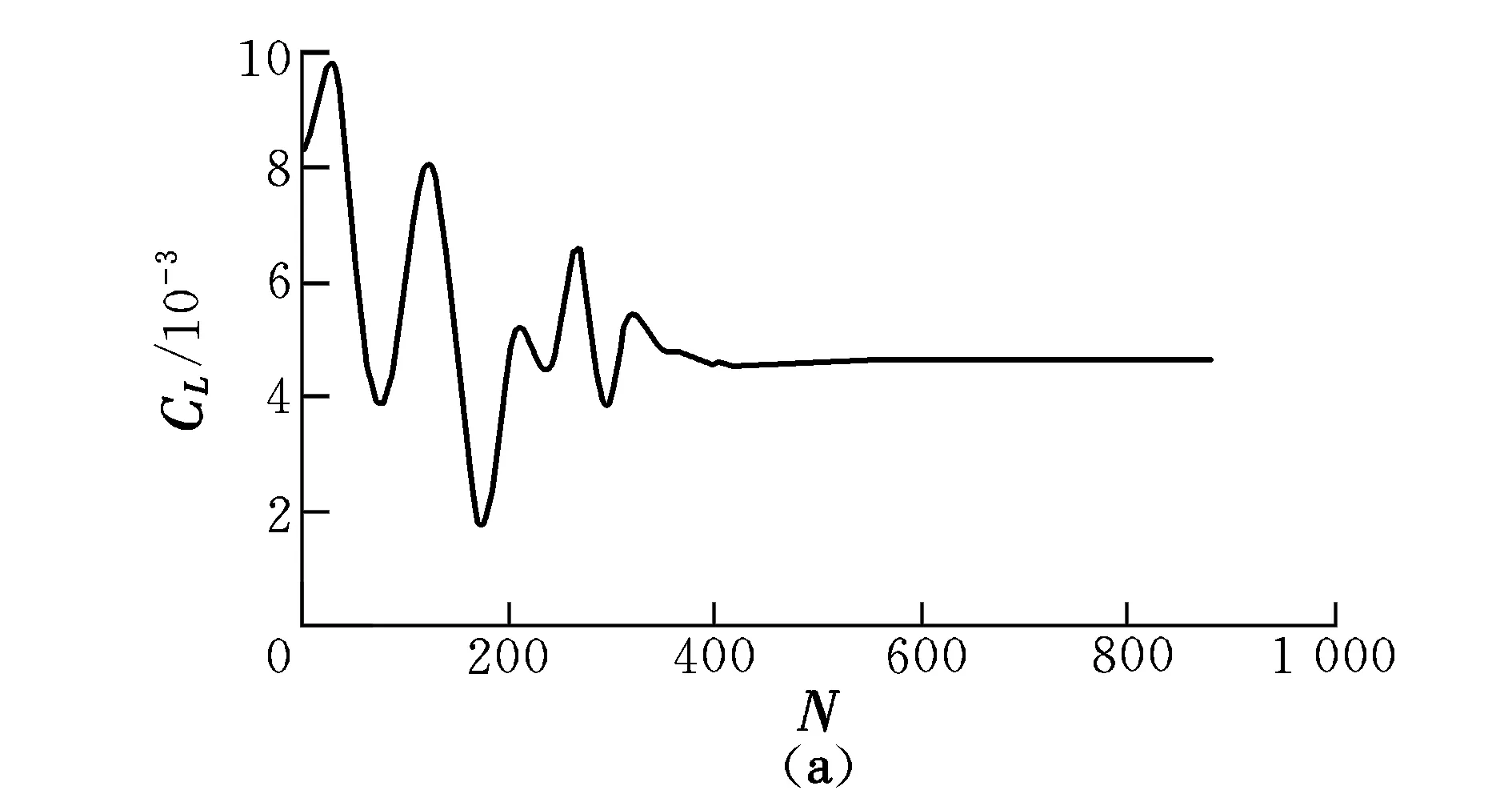
图3　升力系数和阻力系数收敛情况Fig.3　Convergent graphs of CL and CD

图4为航行器在Ma=0.72和0°迎角下飞行时的表面压力云图。可以看出,航行器头部、弹翼、尾翼前缘、弹翼槽突出处受到的压强最大,头部与弹身、弹身与尾部过渡区域形成低压区。在水中航行时,空泡常常产生于头部与弹身过渡的低压区。

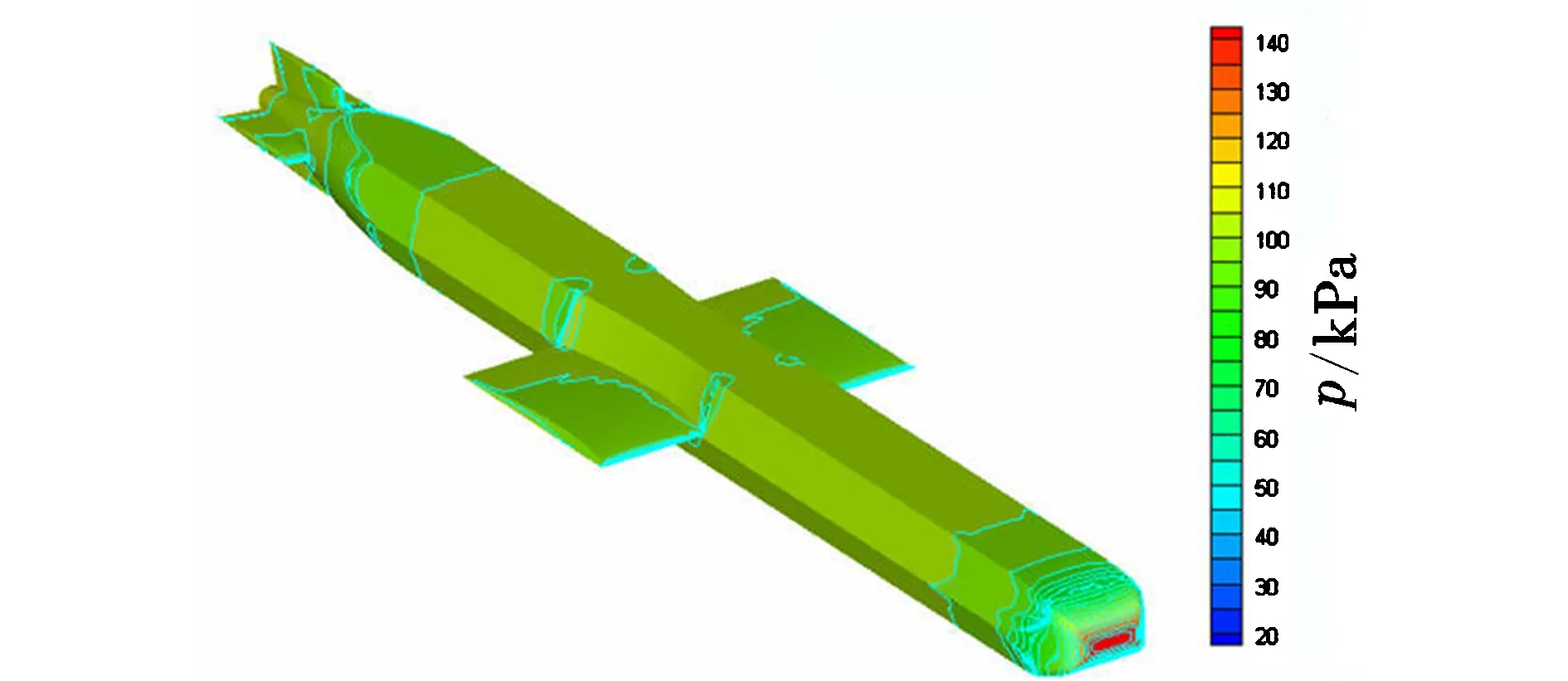
图4　航行器空中飞行压力云图Fig.4　Pressure contour of flight state in the air

由于航行器外形发生变化,在计算水中外形动力系数时所用参考面积为水中模型最大截面积0.18 m2,空中所用参考面积为航行器弹翼面积3.97 m2。航行器在空中和水中的阻力、升力和俯仰力矩随迎角的变化曲线如图5～图7所示。图中曲线为通过三阶最小二乘法对仿真试验数据点进行拟合的结果。

图5　阻力随迎角的变化曲线Fig.5　Curves of the drag changing with the AOA

由图5可以看出,随着迎角从-45°变化到45°,阻力基本上以0°线呈对称分布,且0°线右边部分变化趋势略快于左边部分,这是由于航行器外形上下不完全对称造成的。迎角从0°变化到45°,阻力随迎角增大而变大,这是由于航行器在迎角变大的过程中,在速度方向上的投影面积增大,使航行器所受压差阻力迅速变大。在-10°～10°迎角之内,阻力变化比较平缓,当迎角超过10°之后阻力迅速增大。航行器在空中飞行的阻力变化较在水中航行阻力变化平缓,通过收缩弹翼较大程度地减小了阻力。

图6　升力随迎角的变化曲线Fig.6　Curves of the lift changing with the AOA

由图6可以看出,升力在迎角从-45°变化到45°过程中都是增大的;水中的变化明显快于空中的变化过程,但这相对于没有外形变化的航行器已经有较大改善。可以预见,如果进一步降低水中速度,水中升力曲线则能够匹配上空中升力曲线。在-2°～2°的迎角内,水中航行升力曲线与0°线相交于原点附近,而空中飞行升力曲线与0°线相交于原点上方,这是由于增加了非对称机翼使迎角为0°时产生了正升力。航行器在迎角4°以上能够实现空中水平飞行,水中水平航行迎角在2°附近,航行器在空中、水中均有较大的富裕升力做机动。

图7　俯仰力矩随迎角的变化曲线Fig.7　Curves of the pitching moment changing with the AOA

由图7可以看出,俯仰力矩在迎角从-45°变化到45°过程中不断增大;俯仰力矩对迎角的导数大于0,航行器是静不稳定的;空中变化过程平缓,相对于水中航行更加稳定。

5结束语

本文设计了一种可改变外形的水空跨介质航行器,并通过Fluent对所建模型进行仿真,得到了航行器在各个工况下的阻力、升力、俯仰力矩数值。分析

发现:通过改变外形,航行器兼顾了鱼雷和巡航导弹的飞行性能,在较小的迎角范围内阻力较小,升力能够实现水平飞行/航行,且有较大的富裕升力;相对于没有外形改变的航行器,其水空航行性能有较大改善。在接下来的工作中,将重点研究航行器跨越水面过程流体动力特性和弹翼展开时对航行器空中弹道的影响,为跨介质航行器的设计和试验提供参考。

参考文献：

[1]齐铎,冯金富,李永利.具有水空介质跨越能力的反舰武器[J].飞航导弹,2014(11):78-80.

[2]张佳强.潜-飞两栖导弹动力学特性研究[D].西安:空军工程大学,2012.

[3]贺泳.美国海军水面舰艇导弹防空体系分析[J].现代防御技术,2006,34(4):20-23.

[4]赵洪章,岳春国,李进贤.基于Fluent的导弹气动特性计算 [J].弹箭与制导学报,2009,27(2):203-205.

[5]朱信尧,宋保维,单志雄,等.海底定点停驻无人水下航行器流体动力特性分析 [J].上海交通大学学报,2012,46(4):573-578.

[6]纪兵兵,陈金瓶.ANSYSAICEMCFD网格划分技术实例详解[M].北京:中国水利水电出版社,2012:2-13.

[7]胡志强,林扬,谷海涛.水下机器人粘性类水动力数值计算方法研究[J].机器人,2007,29(2):145-150.

[8]王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:7-13.

[9]潘光,施瑶,杜晓旭,等.驻留航行器沉底稳定性的数值分析[J].上海交通大学学报,2012,46(9):1493-1497.

[10]严卫生.鱼雷航行力学[M].西安:西北工业大学出版社,2005:238-240.

(编辑：李怡)

Aerodynamic and hydrodynamic characteristics analysis o morphing submersible aerial vehicle

LIAO Bao-quan, FENG Jin-fu, QI Duo, LI Yong-li, YU Zong-jin

(Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China)

Abstract:Due to the tremendous difference between water and air in physical properties,it’s hard for a vehicle with fixed shape to meet the requirements of moving underwater and flying in the air. A new vehicle, which has the ability of crossing the water surface for several times through changing its shape, was proposed. The vehicle’s aerodynamics and hydrodynamics were studied with CFD. The simulation results show that, this new vehicle can meet the requirements of moving underwater and flying in the air through changing its shape. The vehicle retracts its wings to make the drag smaller in a small angle of attack under water and unfolds the wings to make the lift support flying in air.

Key words:CFD; aerodynamic characteristics; hydrodynamic characteristics

收稿日期:2015-08-24;

修订日期:2015-11-25; 网络出版时间:2016-02-29 16:37

基金项目:国家自然科学基金资助(51541905)

作者简介:廖保全(1991-)，男，四川绵阳人，硕士研究生，研究方向为航空军械总体与控制技术； 冯金富(1964-)，男，江苏泰兴人，教授，博士生导师，研究方向为兵器科学与技术。

中图分类号：TJ762.4

文献标识码：A

文章编号：1002-0853(2016)03-0044-04