输电塔风振疲劳可靠性分析

白海峰， 刘 兴

（大连交通大学 土木与安全工程学院，辽宁 大连 116028）



输电塔风振疲劳可靠性分析

白海峰， 刘 兴

（大连交通大学 土木与安全工程学院，辽宁 大连 116028）

摘要：基于时域理论研究输电塔在风振作用下的疲劳可靠性问题。本文采用Davenport谱模拟脉动风速，通过分析计算杆件内力，得到风荷载时程数据。利用分析软件SAP2000建立结构的有限元模型，将时程荷载施加到结构有限元模型上，求得输电塔关键杆件应力时程响应。采用雨流法统计分析应力时程数据，得到应力循环幅值及其应力均值。基于疲劳理论的Basquin方程、Miner累积损伤准则以及Goodman修正方程，推导出处理疲劳问题的概率数学模型。结合平均风的分布概率以及计算结构疲劳寿命的方法，得到关键杆件在一定可靠度下的疲劳寿命。通过文章分析可知，随着可靠度数值的变化，结构的疲劳寿命相差极大。

关键词：输电塔；风振；可靠性；疲劳寿命

0 引言

众所周知，输电塔体型高大，结构柔度高，且常年工作在户外，风对输电塔结构的稳定性与安全性影响较为严重。输电塔在风荷载作用下发生疲劳事件，致使电线短路甚至倒塔。因此分析输电塔疲劳可靠性和疲劳寿命是一项很重要的课题，对工程应用中的输电塔结构设计和加固修复提供了理论依据。

早在20世纪80年代，国外学者在海岸工程领域开始关注高耸结构的疲劳损伤问题，当时的研究方向主要是波浪荷载对海洋沿岸结构的疲劳破坏［1］。我国学者邓洪洲、屠海明等人基于宽带随机理论，计算得到谱宽参数ε和修正系数λ，最后分别采用等效窄带法和等效应力法分析结构疲劳累积损伤值［2］；王世村、孙炳南等人分析了单杆塔的疲劳受力问题，提出一种等效窄带法，分别计算背景应力和共振应力的作用［3］。

疲劳损伤是由多种随机因素共同作用而产生的结果，因此可以将疲劳损伤视为一个随机事件，从统计学角度构建疲劳分析模型，解决疲劳累积损伤问题是合理的［4］。本文以Basquin方程和Miner理论为基础，采用一个统计参数代替应力和材料强度极限对结构的疲劳作用，构造出一个损伤的概率模型。结合雨流法处理应力数据，得到杆件在某可靠度下的疲劳寿命。

1 风荷载模拟

根据大量风速观测记录，可以知道大气中的瞬时风包括平均风和脉动风。其中平均风是指在10min中内处于稳定状态的风，而脉动风则是毫无规则的变化，一般变化周期最长也就在两三秒内。任意瞬时风速［5］均可表示为平均风速和脉动风速之和。

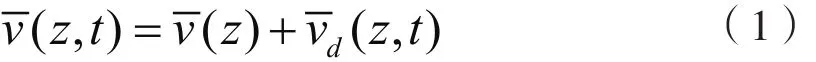
平均风对结构影响可以视为静力作用。考虑到地面建筑物或其他高物体对低空风速的影响，平均风速一般采用Davenport公式描述平均风剖面，

式中：z表示高度值； α是地面粗糙度系数，具体取值可参考文献［3］；代表10m高度处的平均风速，服从Weibull分布。

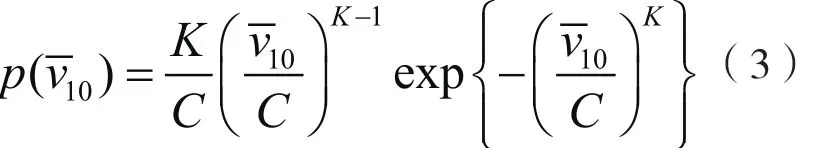
式中：K=1.91， C =5.57［6］。

本文假设脉动风速是一系列均值为零的高斯平稳随机过程，以Davenport谱描述脉动风速谱密度函数：

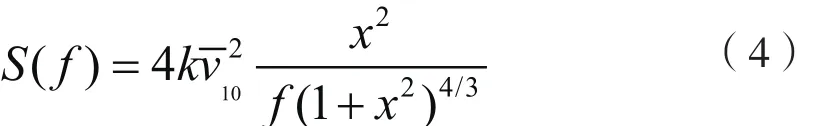
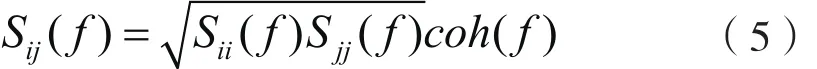
式中：Sii（ f）为i点的功率谱密度函数，具体表达式如式（4），coh（ f）表示功率谱密度函数的相干函数平方根，Davenport给出了具体公式：

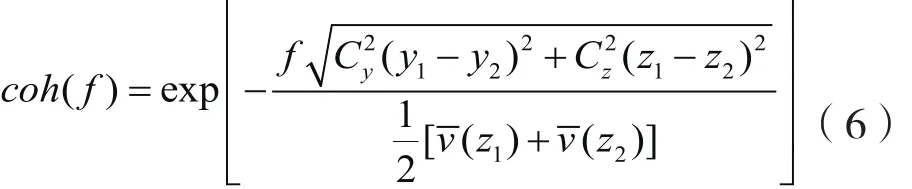
式中：Cy=16，Cz=10，表示空间任意两点衰减系数，zi和yi分别表示空间点的竖向和水平坐标。

本文将模拟的风荷载简化为13个点，作用到输电塔的相应位置，如图1所示，图中有关参数如表1所示。

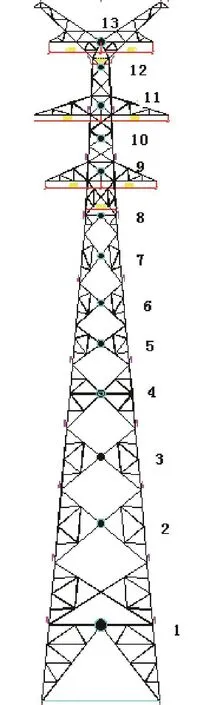
图1　风模拟点位置Fig.1 Loading points of wind in simulation model

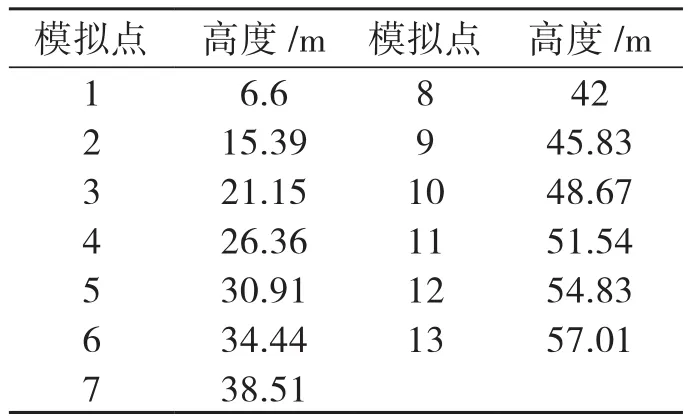
表1　塔体风荷载模拟点高度

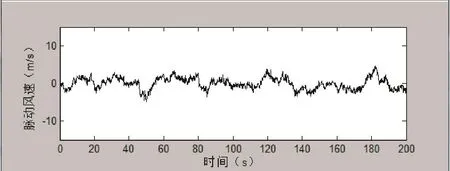
图2　模拟脉动风第2点风速时程Fig.2 Wind velocity time history of point 2

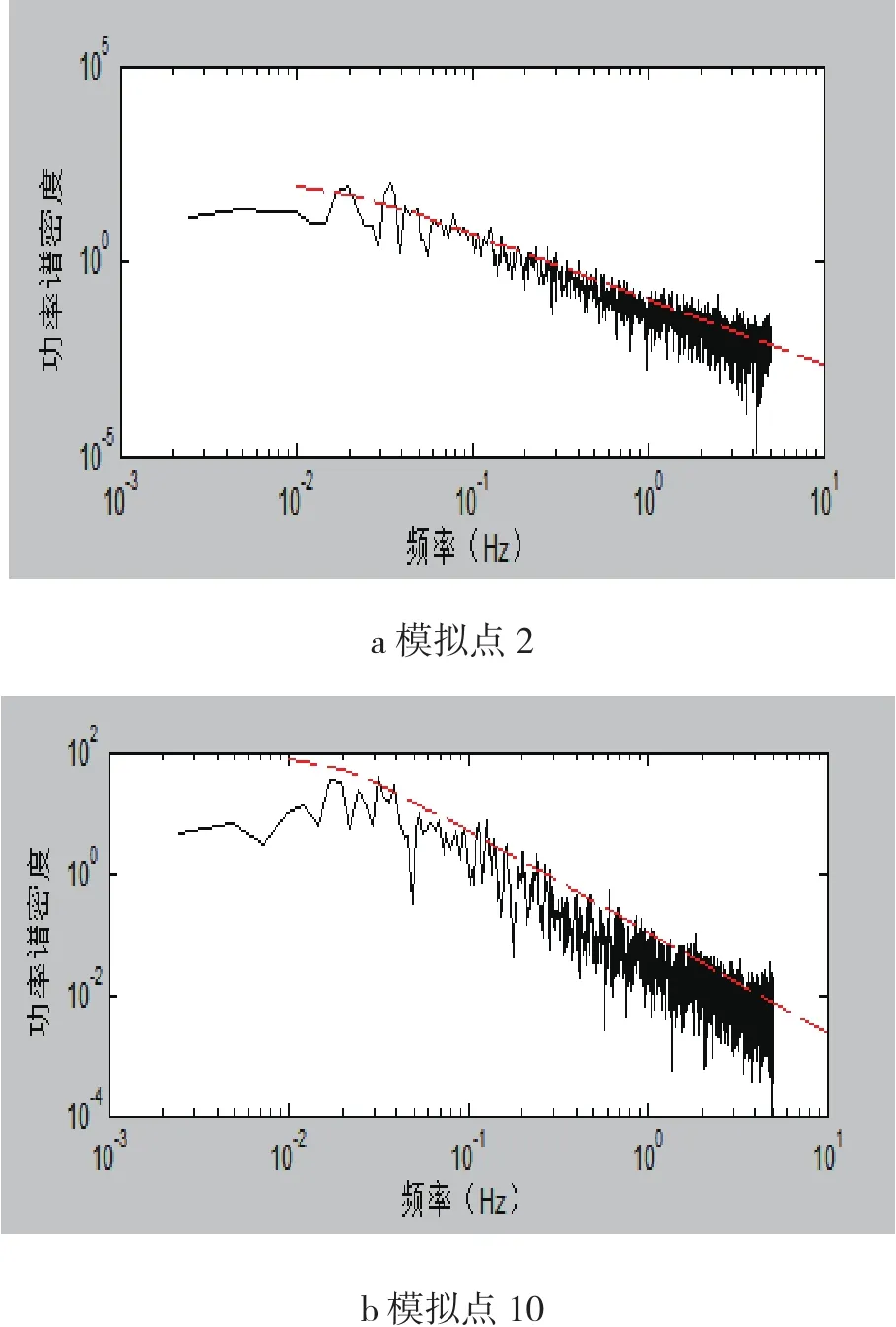
图4　模拟点模拟风谱与目标风谱比较Fig.4 Pulsing simulation wind spectrum and the target spectrum

根据以往文献资料可以获知，对输电塔结构疲劳产生主要作用的风速集中在3～15m/s［7］。在脉动风模拟过程中，顺风向取Kaimal谱，常数k取值0.4。图2-3描述了模拟点2和10的风速时程响应（对应的10m高度处的风速为10.5m/s）。

为了核实该方法的正确性，比较模拟谱与目标谱，如图4所示。由图可知，两种功率谱的趋势保持一致，表明该方法是合理有效的。

2 塔体模型动力分析

2.1 输电塔有限元模型

本文采用单塔有限元模型进行疲劳分析，将导地线、 绝缘子金具等简化为集中质量，施加在塔体横担相应位置。塔身高64m，呼高45m，水平方向跨度600m，图5为使用SAP2000分析软件建立的输电塔模型，以塔体自重为前提，进行模型非线性动力分析。

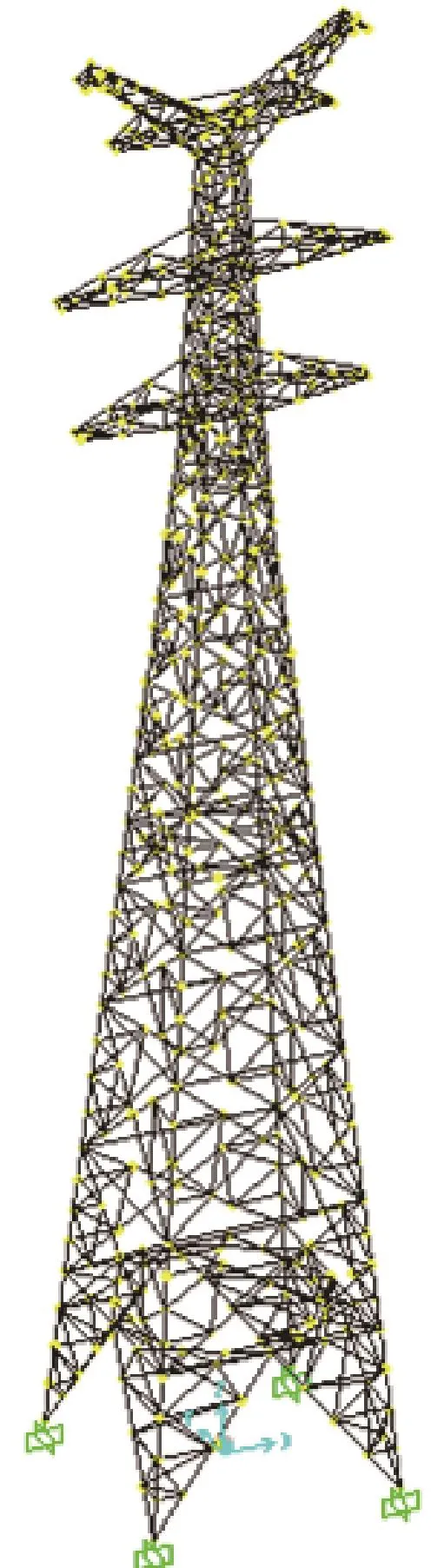
图5　输电塔疲劳分析模型Fig.5 Fatigue analysis model of transmission tower

2.2 非线性分析

通过对输电塔静力分析，确定塔体几个关键杆件［8-9］，对关键杆件进行疲劳分析，关键杆件如图6所示。在对输电塔施加时程风荷载时，时间步长取值0.1s，分析总时长600s，限于篇幅，本文只展示出杆件为6、2360、627三根杆件的风速为13.5m/s时的应力时程图，在分析过程中只计算顺风向。为视图方便，文中仅展示出前60s的应力时程数据。

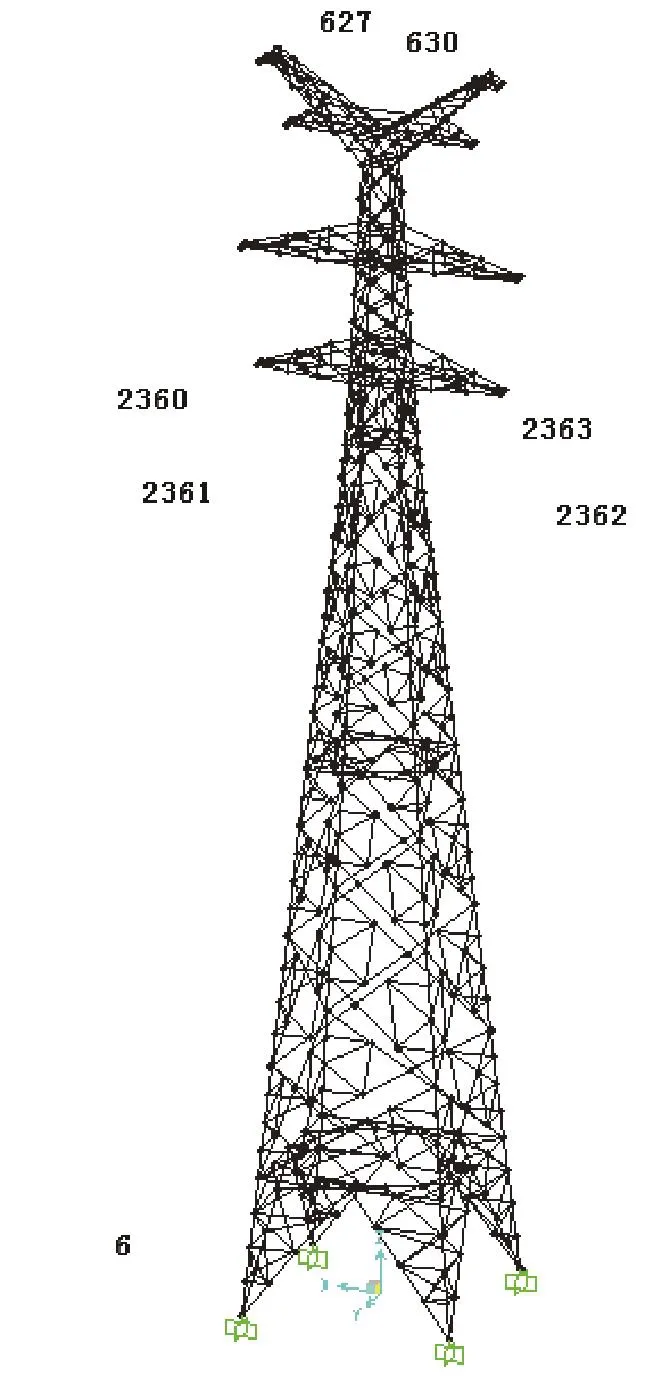
图6　输电塔典型杆件图Fig.6 Typical part of transmission tower

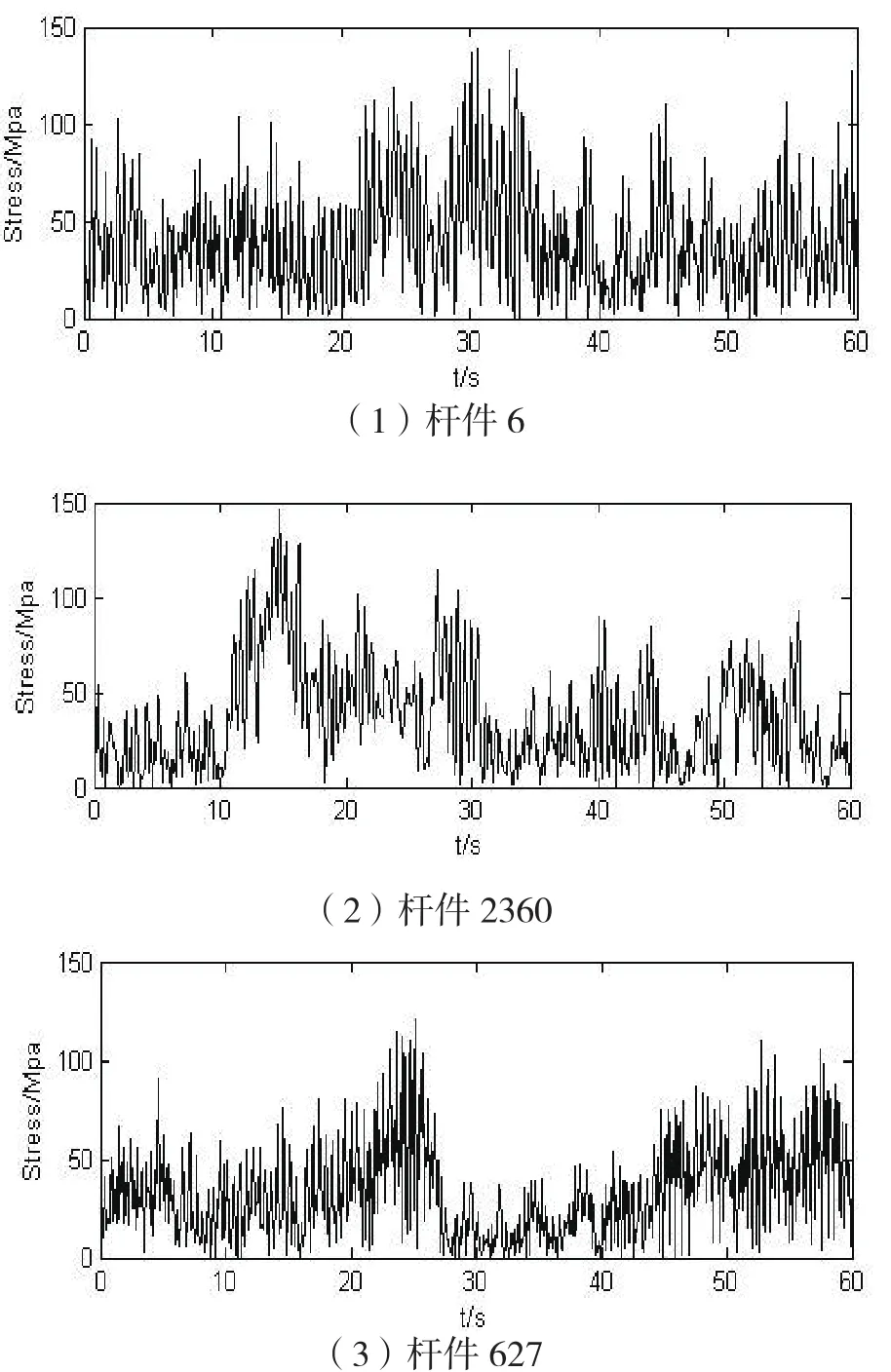
图7　关键杆件应力时程Fig.7 Stress time history of key parts

2.3 雨流法分析

Matsuishi和Endo［10］首次提出雨流法的概念，Dolwing通过实验加以证明，并验证了该方法的精确性。雨流法能够精确统计出时程数据的所有回转点，记录下所有点的滞回数，得到应力循环次数及其对应的均值。通过前文提出的方法计算出关键杆件内力时程，运用雨流法对时程数据进行分析记录，得到杆件的幅值（图8）和均值（图9）的频次图。

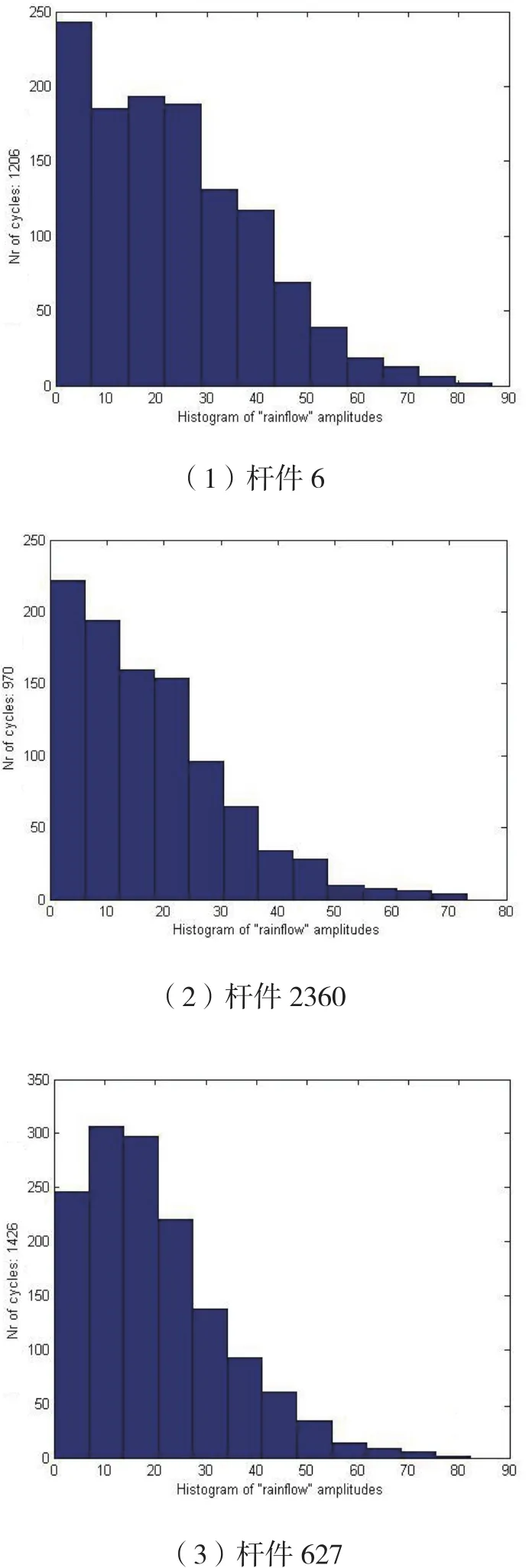
图8　应力幅值频次图Fig.8 Frequency diagram for stress amplitude

图9　应力均值频次图Fig.9 Frequency diagram for mean stress

3 结构疲劳可靠度分析

3.1 疲劳累积损伤

在循环荷载作用下，结构内部发生损伤累积事件，随着损伤值递增，达到某一数值时，结构发生断裂破坏。目前工程或学术上解决疲劳损伤问题，普遍应用的是S—N曲线。疲劳经典理论中，在应力比R下的S—N曲线可以用Basquin方程进行描述：

不失一般性，令R=-1，则iσ和N分别为应力幅值及该应力作用下的循环次数，m和C为与结构材料、应力比和加载方式有关的常数［11］。Miner累计损伤公式为：

式中： ni为某种应力循环的实际循环次数，Ni为对应的应力失效循环次数。结合式（7）和（8），可以得到：

对于均值不为零的时程应力，采用Goodman方程进行调整，考虑平均应力对杆件的影响，则有：

根据方程（11），定义疲劳累积损伤D和疲劳强度K为：

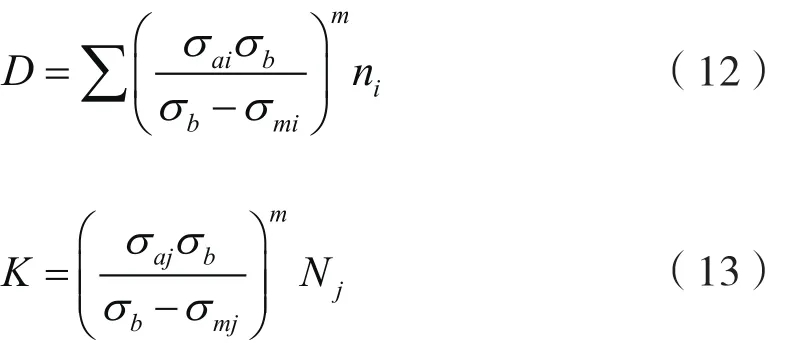
式中D用σai、σmi、bσ和m等变量描述，ni为一个随机变量。其中bσ和m反映了材料特质对累积损伤的影响，σai和σmi反映了应力循环幅值对结构疲劳损伤的影响。疲劳强度K是一个随机变量，可通过实验得到分布情况，通过对数据的计算，可以得到描述疲劳强度K的一组样本。假设在不同应力下得到n个描述K的样本值，对n个样本数据进行分析，可以得到疲劳强度K的分布参数及对应的分布规律。通过试验知道K服从对数正态分布［12］，即：

式中：uk和kσ表示正态分布的参数。本文分析的输电塔关键杆件由钢材Q345制造，参考文献［10］，可以得到关于Q345的材料参数。

3.2 疲劳可靠度分析

结构的疲劳失效可理解为一个随机事件，若强度K已知，利用公式可以计算得到累积损伤D，记R为疲劳可靠度参数，则：

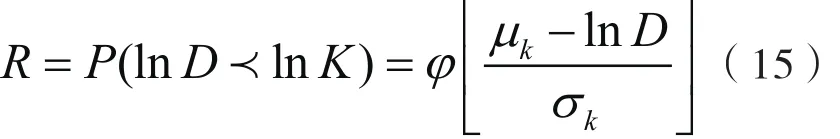
上式是基于Goodman方程调整后的计算式，因此可用于计算等幅疲劳和变幅疲劳的可靠度。由上式可知，若已知结构的可靠度，可以计算在可靠度为R的前提下承受的累积损伤D。

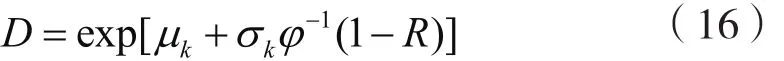
联立上述公式，可以得到可靠度为R时对应的疲劳寿命：

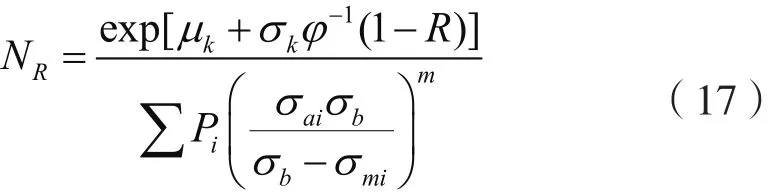
式中：Pi表示应力为σai时的实际循环次数占总循环次数的比例。由公式（3） 可以拟合出10m高度平均风速的离散型分布概率，如图9所示。

通过第一节给出的方法模拟风荷载，并施加到输电塔结构，从而计算出关键杆件的应力时程数据，采用雨流法，统计分析时程数据，计算出杆件的累积损伤值，结合本文描述的方法得到塔体结构可靠度和疲劳寿命。

依据上表所示方法，可以得到其余4根杆件的累积损伤如表3所示。

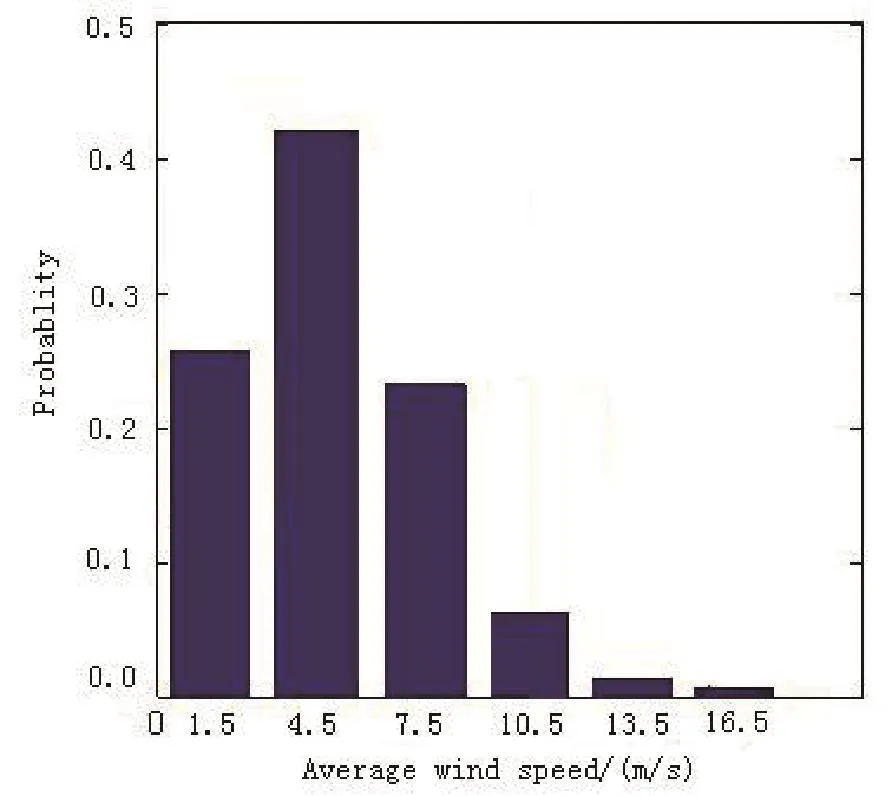
图9　10m平均风速的离散型分布图Fig.9 Distribution of average wind speed at height of 10m

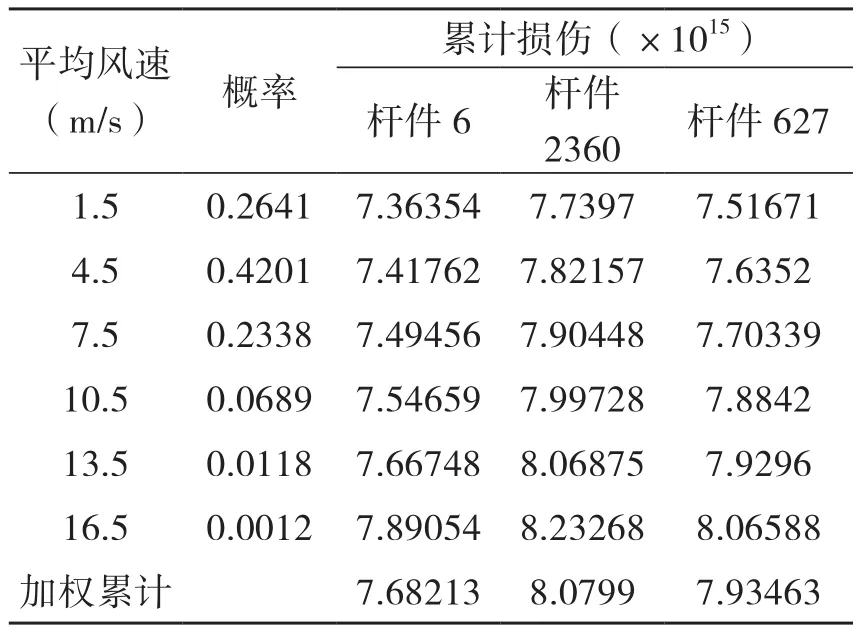
表2　3根关键杆件累积损伤

表3　其余关键杆件累积损伤

表2-3给出的是7根关键杆件在10min内各平均风速作用下的累积损伤数值，其中杆件2361累积损伤最大，因此可以将杆件2361作为计算输电塔整体疲劳寿命的依据。依据式（16）可以得到可靠度为0.95、0.99、0.999、0.9999时结构可以承受的最大累积损伤数据。

表4　杆件承受最大累积损伤

表中β=Φ-1（R），β是结构可靠度为R时的可靠指标，Φ-1（～）是标准正态分布函数的反函数。

假设输电塔杆件每年承受风荷载时间为365天，因此由上式可以得到关键杆件在各种可靠度情况下的疲劳寿命值（单位为年）。

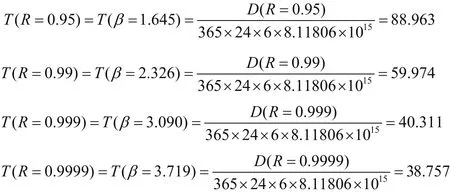
4 结论

在脉动风模拟的前提下，将输电塔受力特征简化为集中点受力，研究了雨流法在疲劳累积损伤中的应用，计算出在不同可靠度下，关键杆件（塔身）的疲劳寿命值。

（1）通过内力分析，得到铁塔关键杆件的应力时程数据，采用雨流法，得到关键杆件的应力幅值和应力均值，计算结构的疲劳寿命。由结果可以看出，随着结构可靠度的增加，杆件所能承受的疲劳损伤值逐渐降低，在可靠度为0.95时，构件可以工作至少88年，但当可靠度提高到0.9999时，构件的安全工作时间减低至38年，为铁塔设计起到一定的探索作用。

（2）通过文章分析，可以获知塔体在横担与支架连接处最为脆弱，因此在设计输电塔过程中，尤其需要注意该位置处的强度计算。在输电塔施工过程中，也需要特别注意该处的焊接情况，不要存在裂缝情况。

参考文献：

［1］Wyatt T A. An assessment of the sensitivity of lattice towers to fatigue induced by wind gusts ［J］. Eng Struct，1984， 6（4）： 262-267.

［2］邓洪洲， 屠海明， 王肇民. 桅杆结构随机风振疲劳研究［J］. 土木工程学报， 2003， 6（4）： 19-23.

［3］王世村， 孙柄楠， 叶尹. 自立式单杆输电塔顺风向风振疲劳分析［J］. 浙江大学学报， 2005， 39（2）： 1180-1184.

［4］Repetto M P， Solaria G. Wind-induced fatigue collapse of real slender structures［J］. Engineering Structures， 2010，32（12）：3888-3898.

［5］黄本才. 结构抗风分析原理及应用［M］.上海：同济大学出版社，2001.

［6］王之宏. 栀杆结构的风振疲劳分析［J］.特种结构，1994，11（3）：3-8.

［7］邓洪洲， 屠海明.栀杆结构随机风振疲劳研究［J］. 土木工程学报，2003， 36（4）：19-23.

［8］张卓群， 李宏男， 李东升，等. 高压输电塔结构的疲劳寿命分析［J］. 电力建设， 2014， 35（1）： 14-18.

［9］孙 彤， 林友新， 张卓群，等.角钢高压输电塔疲劳寿命计算与分析［J］. 防灾减灾学报，2013， 29（3）： 13-19.

［10］Matsuishi M， Endo T. Fatigue of metals subjected to varying stress［C］. Japan Society of Mechanical Engineers，Fukuoka， Japan， 1968.

［11］董兴建， 李鸿光， 孟光. 岸桥起重机随机风振疲劳可靠性分析［J］. 振动工程学报， 2013， 26（6）： 901-906.

［12］胡宗武， 乐晓斌.机械结构概率设计［M］. 上海：上海交通大学出版社， 1995.

RELIABILITY ANALYSIS ON WIND-INDUCED FATIGUE FOR TRANSMISSION TOWER

BAI Hai-feng， LIU Xing
（Dalian Jiaotong University School of Civil and Safety Engineering， Liaoning Dalian 116028， China）

Abstract：Wind-induced fatigue reliability analysis for transmission tower is conducted using time domain method. In this paper， it uses Davenport power spectral to simulate the fluctuating wind velocity， and gets the wind load time history data through analysis and calculation of internal force of bar. The finite element model of the structure is established by using the software SAP2000， and applied the wind load time history data， calculate the stress time history of the key bars. To obtain the amplitude of the stress cycle and the mean stress value，the stress time history data were analyzed by means of rain flow method. A methodology for probabilistic modeling of fatigue damage accumulation is developed using Basquin random equations， Miner failure cumulative damage criterion and Goodman fatigue limit correction equation. Combined distribution probability about mean wind speed， and the method of calculating the fatigue life， the fatigue life of the key rods is obtained， so the conclusion of this paper provides some research for the fatigue reliability of transmission tower. Through the analysis of the article， we can know that， with the increase of reliability， the fatigue life of the structure is very different.

Key words：transmission tower； wind vibration； reliability； fatigue life

中图分类号：P315

文献标志码：A

DOI:10.13693/j.cnki.cn21-1573.2016.02.006

文章编号：1674-8565（2016）02-0032-08

基金项目：国家自然科学基金资助项目（项目编号：51378086）

收稿日期：2016-01-19

修订日期：2016-04-18

作者简介：白海峰（1965-），男，教授，主要研究方向为大跨度结构动力响应分析。