上覆煤层开采后下伏煤层渗透性变化规律研究

冯　辉，高　杰，胡钦涛

(1.陕西郭家河煤业有限责任公司，陕西 宝鸡 721505；2.宁夏理工学院，宁夏 石嘴山 753000)

上覆煤层开采后下伏煤层渗透性变化规律研究

冯辉1，高杰2，胡钦涛1

(1.陕西郭家河煤业有限责任公司，陕西 宝鸡 721505；2.宁夏理工学院，宁夏 石嘴山 753000)

[摘要]上覆煤层开采后，掌握下伏煤层渗透率的变化规律是瓦斯抽采的关键。采用FLAC3D对上覆煤层开采进行数值模拟，模拟结果显示：当膨胀变形为正时，下伏煤层煤体被加载压缩；当膨胀变形为负时，下伏煤层煤体被卸载拉伸。采用瞬态压力脉冲法测定下伏煤层的渗透率，由实验室加载-卸载实验得到渗透模型：加载过程中渗透率与轴向应变成负指数函数关系；卸载过程中渗透率与轴向应变成正指数函数关系。最终得出膨胀变形值与渗透率方程关系，以此分析上覆煤层开采后下伏煤层渗透率的演化规律。

[关键词]下伏煤层；渗透率；瓦斯；加载-卸载

大量实践证明，煤层开采过后，邻近煤岩体的原有地应力的平衡状态被打破，导致顶底板的煤岩体出现移动变形、膨胀卸压，从而产生大量纵向和横向的裂隙和孔隙。在此过程中，邻近煤层原有的平衡瓦斯压力也被打破[1-2]，发生卸压现象。上覆煤层开采引起下伏煤层的变形，上覆煤层采动过程中，下伏煤层经历了不同的受力过程，即加载-卸载过程；自从哈秋舲[3-5]提出“卸荷岩体力学”以来，不同的学者分别采用卸载实验来研究卸载状态下岩石的强度特征、变形破坏特征、破坏形式等，普遍证实了加、卸载不同力学路径下，煤岩体的力学性质有着本质的区别[6-8]。本文以上覆煤层开采为背景，通过卸载实验，研究下伏煤层卸载煤体的渗透性规律。

1试验工作面概况

山西吕梁离柳矿区某矿3号煤层3313工作面地面标高942～1089m，工作面标高为560～605m，工作面走向长度为1633m，倾向长度为170(60)m。煤层结构简单，近似水平，倾角平均4°，煤层平均厚度2m。3313工作面地质构造简单，基本为单斜构造，埋深382～484m，瓦斯压力0.21～1.03MPa，瓦斯含量2.35～11.29m3/t。3313工作面实际配风量935m3/min，绝对瓦斯涌出量14.9m3/min。工作面煤层柱状图如图1所示。

图1　3313工作面煤层柱状

2上覆煤层开采数值模拟

2.1数值模型建立

采用FLAC3D对上覆煤层开采进行数值模拟，数值计算模型如图2所示。模型大小为400m×400m×200m，底部边界固定，四周为滚轴边界，上部施加原岩应力6.5MPa，水平施加4MPa应力。

图2　FLAC3D数值模型计算

为获得上覆煤层开采后下伏煤层膨胀变形情况，在4号煤层下伏煤层顶板及底板布置位移监测点，监测点之间的距离为5m，如图3所示。

图3　被保护层监测点位置

2.2模拟结果分析

利用FLAC3D本身携带的hist命令将保护层开挖50m，100m和200m以后的顶板、底板位移值进行提取，然后利用Matlab计算下伏煤层在上覆煤层开挖不同距离后的膨胀变形变化情况，如图4所示。

下伏煤层的膨胀变形率是指下伏煤层底板、顶板位移之差与下伏煤层厚度的百分比，它可以用来判定下伏煤层的卸压程度，公式为：

(1)

图4　上覆煤层开挖不同距离下伏煤层膨胀变形情况

式中，S为煤层膨胀变形率，‰；d顶板煤层顶板位移，m；d底板为煤层底板位移，m；m为煤层厚度，m。

由图4可知，膨胀变形有正负之分，当膨胀变形为正时，下伏煤层煤体被加载压缩；当膨胀变形为负时，下伏煤层煤体被卸载拉伸，具体结果如表1所示。

表1　被保护层膨胀变形结果

3加载-卸载实验及下伏煤层渗透率变化

实验采用的煤样取自下伏煤层，将煤样制作成型煤，通过煤岩应力-渗透耦合仪进行加-卸载实验，实验采用的力学路径为固定轴向位移卸围压和固定差应力卸围压[9]。将试样的初始围压设定为8MPa和6MPa，然后进行加载。当加载至屈服点后稍许进行卸载实验，在卸载过程中采用瞬态压力脉冲法测定试样渗透率。

3.1瞬态压力脉冲法测定渗透率的原理

采用瞬态压力脉冲法进行渗透率的测定，其方程[10-11]为

Pup(t)-Pdown(t)=(Pup(t0)-Pdown(t0))e-αt

(2)

α=(kA/μβL)(1/Vup+1/Vdown)

(3)

式中，P为储气罐的压力，MPa；α为气体压力随时间衰减过程中的指数拟合因子；k为渗透率，mD；A为试样面积，m2；L为试样长度，m；V为储气罐的体积，mL；μ为动力黏度，MPa·s；β为气体压缩因子，MPa。

当Vup=Vdown时，在不计管路体积的条件下，公式(3)可简化为

(4)

根据公式(2)和(4)并结合压力脉冲曲线算出α，由于L和A值是已知的，将α值代入公式(4)，就可以得到渗透率k值的大小。瞬态压力脉冲曲线如图5所示，其中横坐标为时间，纵坐标为电压，通过计算机可以获得每时刻所对应的电压值，由电压值可转换成上下游储气罐的压力差(1V≈0.22MPa)，由此根据公式(2)计算出α，然后根据公式(4)计算得出渗透率k。

图5　渗透率测定瞬态脉冲曲线

3.2固定轴向位移卸围压渗透性实验结果

采用瞬态压力脉冲的方法，在初始围压为8MPa和6MPa的条件下固定轴向位移卸载围压，渗透性实验结果如图6、图7所示。

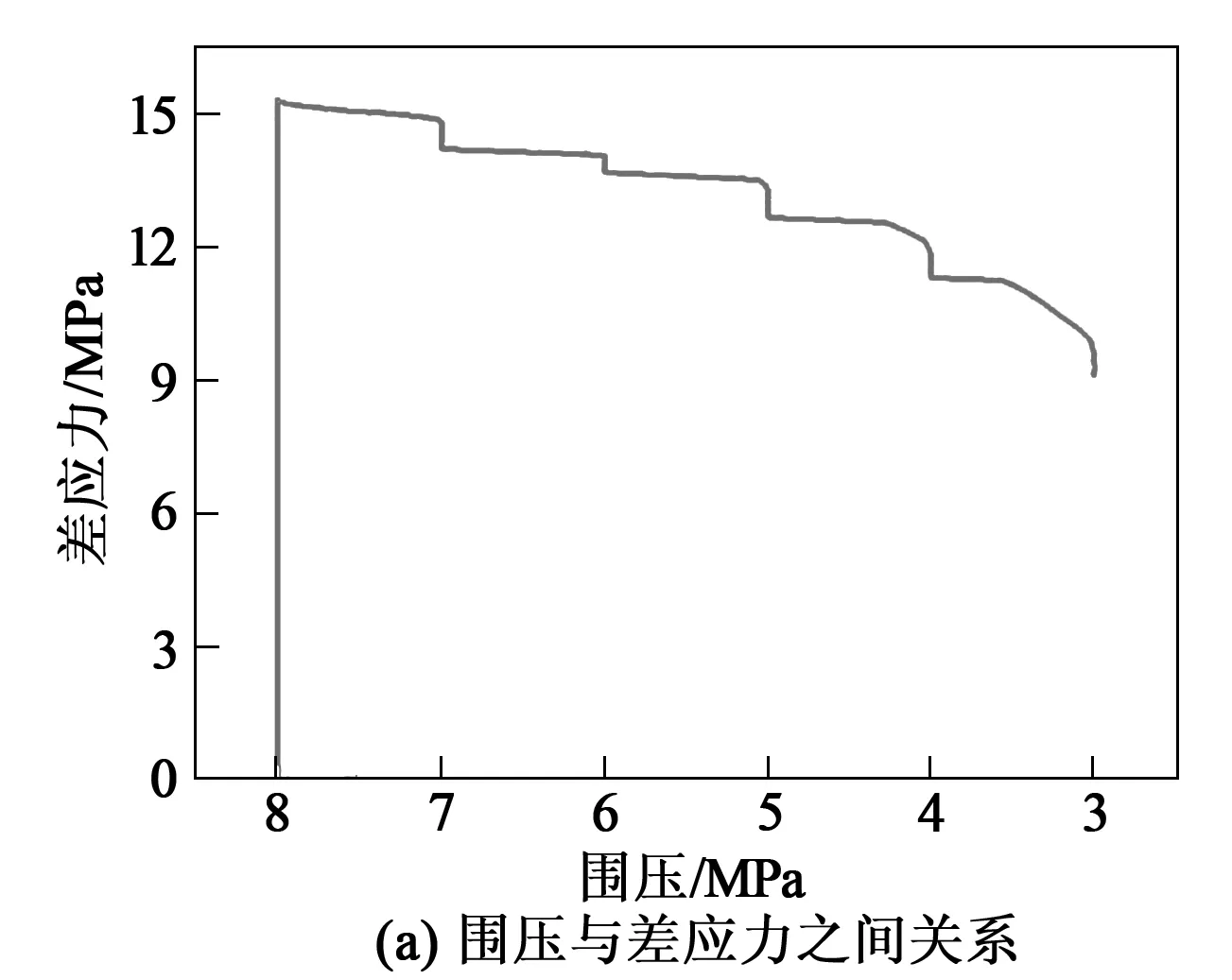
图6　初始围压8MPa固定轴向位移卸围压渗透性变化

由图6、图7可知，固定轴向位移卸围压过程中，初始阶段差应力减小速率缓慢，当试样损伤达到一定程度，随着差应力减小速率迅速增大；试样加载过程中，渗透率逐渐减小，当加载至屈服点后少许开始卸载，此过程中渗透率逐渐增大，且增大速率也逐渐变大。不同围压条件下固定轴向位移卸围压渗透率测定结果如表2所示。

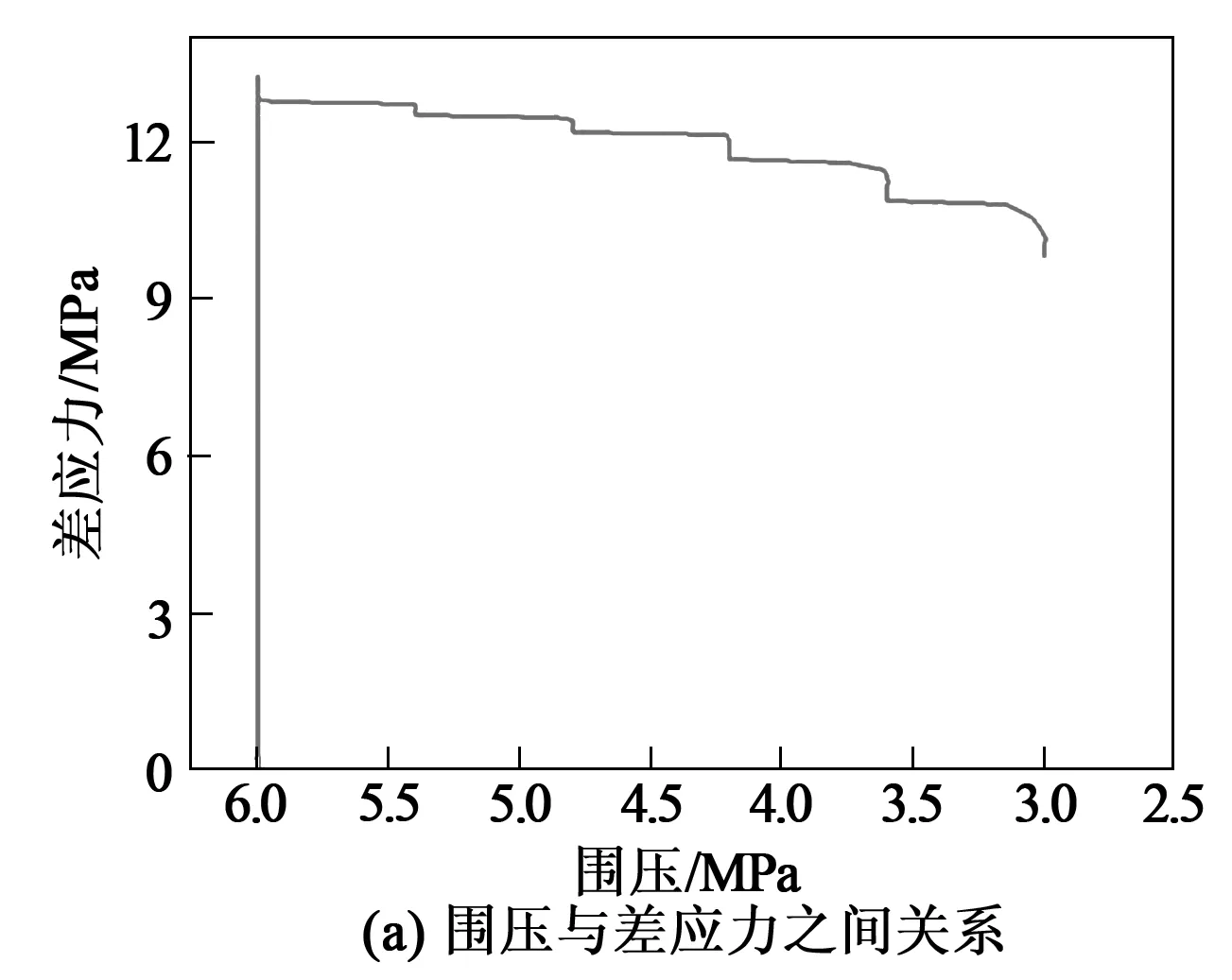
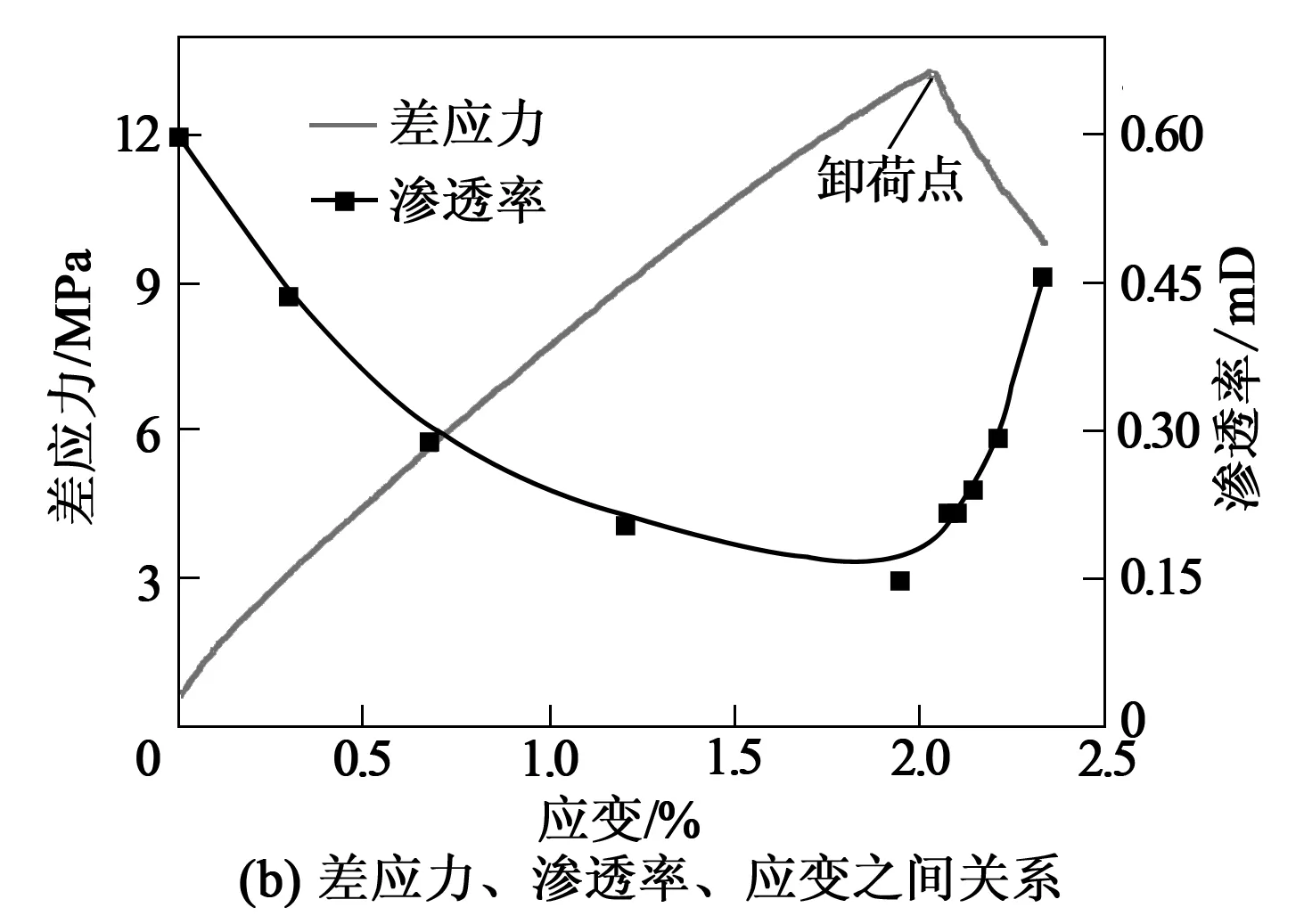
图7　初始围压6MPa固定轴向位移卸围压渗透性变化

表2　不同初始围压下固定轴向位移卸载实验渗透率测定结果

3.3固定差应力卸围压渗透性实验结果

采用瞬态压力脉冲的方法，在初始围压8MPa和6MPa的条件下固定差应力卸载围压，渗透性实验结果如图8、图9所示。

图8　初始围压8MPa固定差应力卸围压渗透性变化

图9　初始围压6MPa固定差应力卸围压渗透性变化

由图8、图9可知，固定差应力卸围压过程中，初始阶段差应力不变，当试样损伤达到一定程度，随着围压的卸载差应力减小速率迅速增大；试样加载过程中，渗透率逐渐减小，当加载至屈服点后少许开始卸载，此过程中渗透率逐渐增大，且增大速率也逐渐变大。不同围压条件下固定差应力卸围压渗透率测定结果如表3所示。

3.4渗透性实验结果

通过两种力学路径的卸载实验得到卸载过程中试样的渗透率，将表2、表3中的数据进行拟合，得到结果如表4所示。

表3　不同初始围压下固定差应力卸载实验渗透率测定结果

表4　煤样轴向应变与渗透率的关系

由表4可知：加载过程中渗透率与轴向应变成负指数函数关系；卸载过程中渗透率与轴向应变成正指数函数关系。

(1)加载过程

k=A1e-B1ε

(6)

(2)卸载过程

k=A2eB2ε

(7)

式中，A1，A2，B1，B2为拟合系数，反应了渗透率对轴向应变的敏感程度。

3.5下伏煤层渗透性变化特征

上覆煤层开采后，下伏煤层受采动影响而发生膨胀变形，即下伏煤层在垂向上受到拉伸或者压缩，这跟实验室得到的渗透模型中的轴向应变具有相似性，因此可以运用模拟得到的下伏煤层膨胀变形代替轴向应变进行解算渗透率。

为简化工程问题而得到煤体的渗透率分布特征，由2.2节得到下伏煤层的膨胀变形值代替轴向应变代入渗透性实验方程即可。由于以此只能获得煤体渗透率的分布特征，而不能得到真正的渗透率的值，因此拟合系数A1，B1，A2，B2大小的选择不影响得出的渗透率的分布特征。根据煤样选取地点实际应力值以及实验室的实验条件，得出的膨胀变形值与渗透率方程关系如表5所示。

表5　膨胀变形与渗透率方程的关系

使用Matlab将膨胀变形值进行整理，代入表5的方程中得到开挖不同距离下伏煤层的渗透率分布情况，如图10所示。

图10　开挖不同距离下伏煤层渗透率变化特征

由图10可知，上覆煤层采动后下伏煤层工作面渗透率出现了渗透率增大区、渗透率减小区和原始渗透率区，且随着上覆煤层的向前推进，下伏煤层渗透率增大区范围在变大；在工作面倾向上渗透率最大处在始采线前方以及停采线后方25～35m范围，最小处在始采线后方以及停采线前方10～15m范围；工作面在走向上渗透率增大最大处在距离风巷、机巷内侧25～35m范围，最小处在距离风巷、机巷外侧10～15 m范围。

4结论

以上覆煤层开采为背景，通过实验室加载-卸载实验，研究下伏煤层卸载煤体的渗透性规律，得到结论如下：

(1)煤体在加载阶段，渗透率逐渐减小，达到卸荷点后的卸载阶段，渗透率迅速增大，且增大速率逐渐变大。

(2)通过对渗透率测试结果的拟合可知，卸载力学路径下，加载阶段，煤样渗透率与轴向应变的关系为k=A1e-B1ε；卸载阶段，煤样渗透率与轴向应变的关系为k=A2eB2ε。

(3)上覆煤层采动后下伏煤层工作面渗透率出现了渗透率增大区、渗透率减小区和原始渗透率区，且随着上覆煤层的向前推进，下伏煤层渗透率增大区范围在变大；在距巷道和切眼向内25～35m处渗透率出现最大值，距巷道和切眼向外10～15m处渗透率出现最小值。

[参考文献]

[1]Yi J，Akkutlu I Y，Karacan C Ö，et al. Gas sorption and transport in coals：A poroelastic medium approach[J]. International Journal of Coal Geology，2009，77(1-2)：137-144.

[2]Ying-ke L，Fu-bao Z，Lang L，et al. An experimental and numerical investigation on the deformation of overlying coal seams above double-seam extraction for controlling coal mine methane emissions[J]. International Journal of Coal Geology，2011，87(2)：139-149.

[3]哈秋舲.岩石边坡工程与卸荷非线性岩石(体)力学[J]. 岩石力学与工程学报，1997，16(4)：386-391.

[4]哈秋舲，刘国霖.长江三峡工程岩石边坡卸荷岩体工程地质研究[M].北京：中国建筑工业出版社，1997.

[5]哈秋舲，张永兴.三峡船闸岩石陡高边坡稳定与控制研究[M].重庆：重庆大学出版社，1997.

[6]吴刚.复杂应力状态下完整岩体卸荷破坏的损伤力学分析[J].河海大学学报，1997，25(3)：44-49.

[7]黄润秋，黄达.卸荷条件下岩石变形特征及本构模型研究[J].地球科学进展，2008，23(5)：441-446.

[8]黄达，金华辉，黄润秋.拉剪应力状态下岩体裂隙扩展的断裂力学机制及物理模型试验[J].岩土力学，2011，32(4)：997-1001.

[9]Chen HD，Cheng YP，Zhou HX，Li W.Damage and permeability development in coal during unloading[J].Rock Mech Rock Eng，2013(46)：1377-90.

[10]Brace, W.F. Walsh, J.B. Frangos, W.T. Permeability of granite under high pressure[J].Journal of Geophysical Research，1968(73)：2225-2236.

[11]Wang，S.G. Elsworth，D. Liu，J.S. Permeability evolution in fractured coal：The roles of fracture geometry and water-content[J].International Journal of Coal Geology，2011，87(1)：13-25.

[责任编辑：施红霞]

Research on Permeability Change Law of Underlying Coal Seam after Overlying Coal Seam Mining

[收稿日期]2015-09-07[DOI]10.13532/j.cnki.cn11-3677/td.2016.03.031

[作者简介]冯辉(1987-)，男，河南商丘人，硕士，从事瓦斯治理工作。

[中图分类号]TD712.52

[文献标识码]B

[文章编号]1006-6225(2016)03-0117-05

[引用格式]冯辉，高杰，胡钦涛.上覆煤层开采后下伏煤层渗透性变化规律研究[J].煤矿开采，2016，21(3)：117-121.