圆环形阵元阵列的三维指向性比较

法　林,王　军,韩永兰,赵　洁,刘世朋

(1.西安邮电大学 电子工程学院，陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)

圆环形阵元阵列的三维指向性比较

法林1,王军2,韩永兰1,赵洁1,刘世朋1

(1.西安邮电大学 电子工程学院，陕西 西安 710121; 2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)

摘要:根据换能器基阵的指向性理论，对圆环形阵列进行分析，采用数值方法，对48个相同的圆环形阵元组成的矩形形式阵列和线阵列组合圆周阵列的指向性进行三维仿真。仿真结果表明，矩形形式阵列的指向性差异会随着长宽比的增大而增大，但同一矩阵形式阵列的指向性随着声频增高而变好；线阵列组合圆周阵旁瓣幅值最小，指向性最优。

关键词:指向性；矩形形式阵列；线阵列组合圆周阵；三维仿真

换能器是声电和电声转换的重要器件，广泛应用于工业、农业、军事、医疗生活等方面。指向性作为衡量换能器性能的一个重要指标，越来越引起人们的广泛关注。换能器制作工艺较复杂、制作难度较大，且体积较小，造成了单个换能器的发射功率有限，接收灵敏度不够高等问题。因此，很少单个独立应用，而是经常把若干个换能器按一定规律排成阵列，以达到所需性能指标的要求。现有的研究中对矩形阵列指向性[1]、圆环形阵元[2]、不同阵元构成的线阵列的指向性[3]进行分析，通过对线性超声换能器阵列的参数优化来改善器指向性能[4]，其都忽略了阵元的尺寸大小，或仅对线阵列和矩形阵列采用二维方式[2]，不能准确直观地反映出整个声场的指向性情况。本文拟设计不同的阵列形式，对不同阵列的指向性采用Matlab进行三维仿真，分析不同形式阵列对指向性的影响。

1基阵指向性理论

指向性是声源振动时声场的重要特性之一。对于多个组合声源构成的基阵，求其指向性时一般采用Bridge乘积定理[9]。

1.1线阵列指向性函数

在xOy平面内N个无指向性的点源均匀排列在一条直线上，如图1所示，其指向性函数为[1]

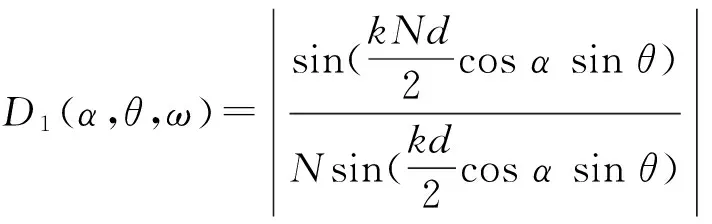
(1)

其中k=2π/λ为波数，λ为波长，d为相邻两阵元之间的间隔，ω为角频率。

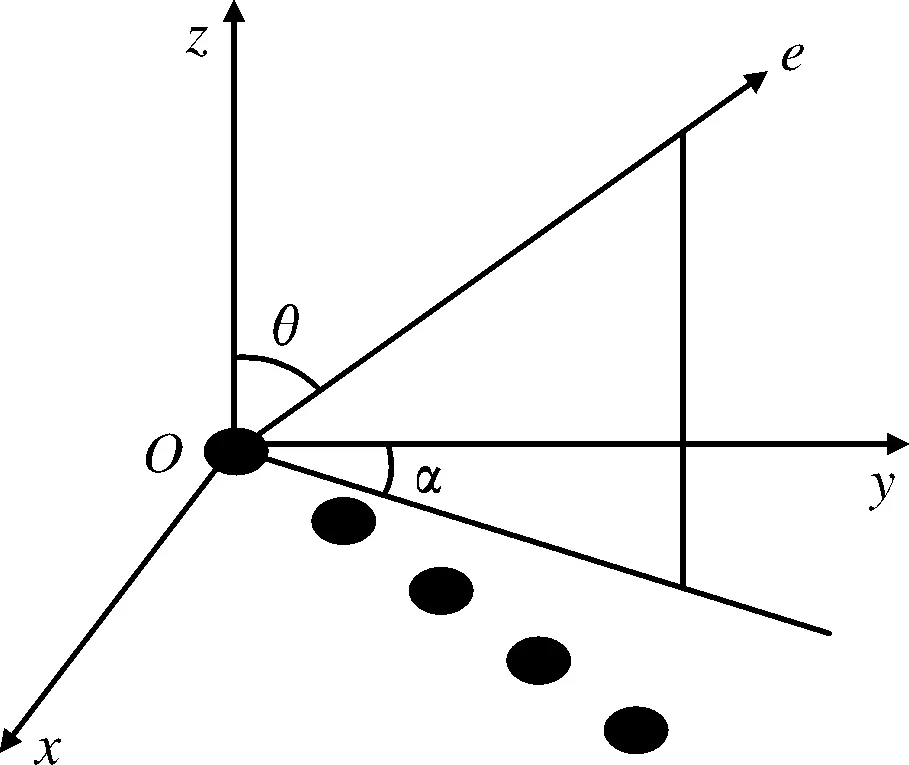
图1　点声元构成线阵列示意图

1.2矩形阵列指向性函数

线列阵组合的矩形形式阵列是由N行M列阵元均匀排列在平面上构成的，d1为阵元行间距，d2为阵元列间距，其指向性函数[1]为

D2(α,θ,ω)=

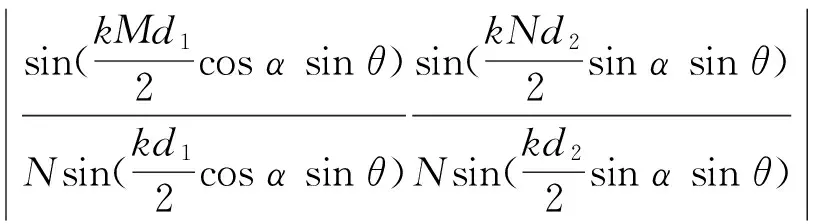
(2)

1.3圆周阵列指向性函数

在xOy平面上，有N个无指向性的点源均匀排列在半径为r的圆周上，结构如图2所示。

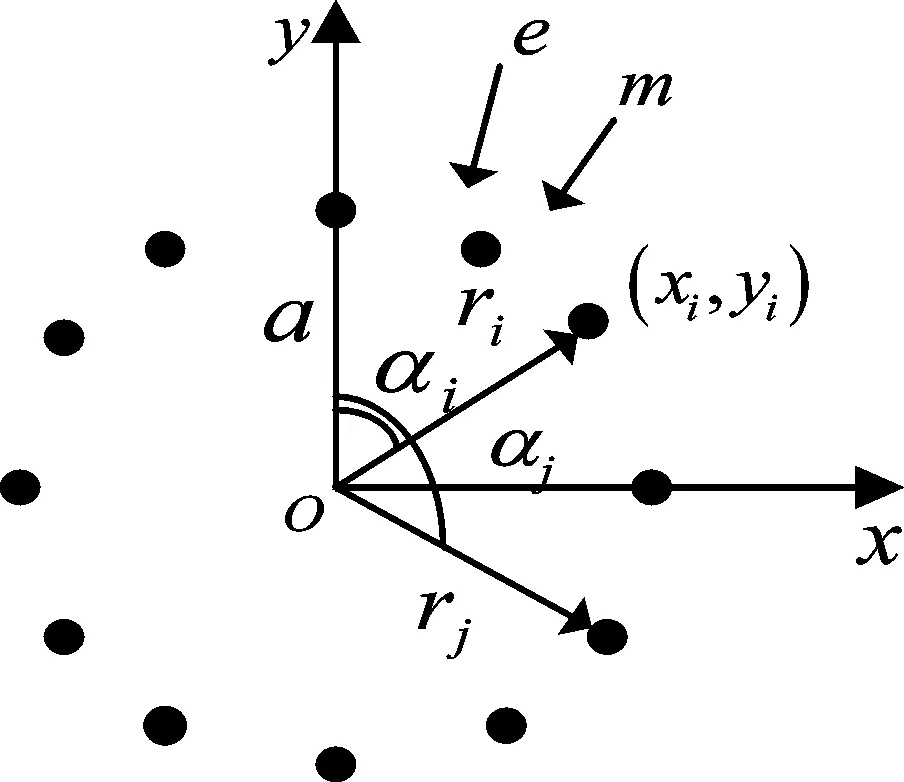
图2　点声元构成圆周阵示意图

坐标原点作为圆的圆心，点(xi,yi)是阵元i的坐标，αi，ri分别为方位角和矢径，e为声线方向的单位向量，m为各阵元经相位补偿后在主极大方向上的单位向量，i、j和k分别为x、y、z方向的单位向量。它对应的指向函数为

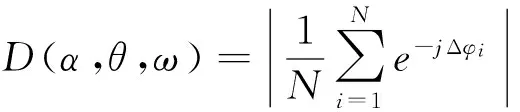
(3)

其中Δφi=k(e-m)·ri，以坐标原点为参考点阵元i在非补偿下的相位

ri=a(sinαii+cosαij)，

e=sinαsinθi+cosαsinθj+cosθk，

αi=i2π/N，

代入式(3)得圆环形阵元组合圆周阵指向性函数

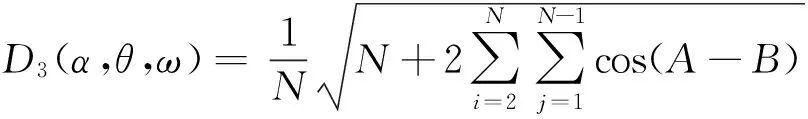
(4)

其中

A=krsinθcos(α-αi)，

B=krsinθcos(α-αj)。

1.4线列阵组合圆周阵指向性函数

N个阵元均匀排列在半径为r的圆周上组成圆周阵，沿z轴方向均匀排列M个圆周，结构如图3所示。

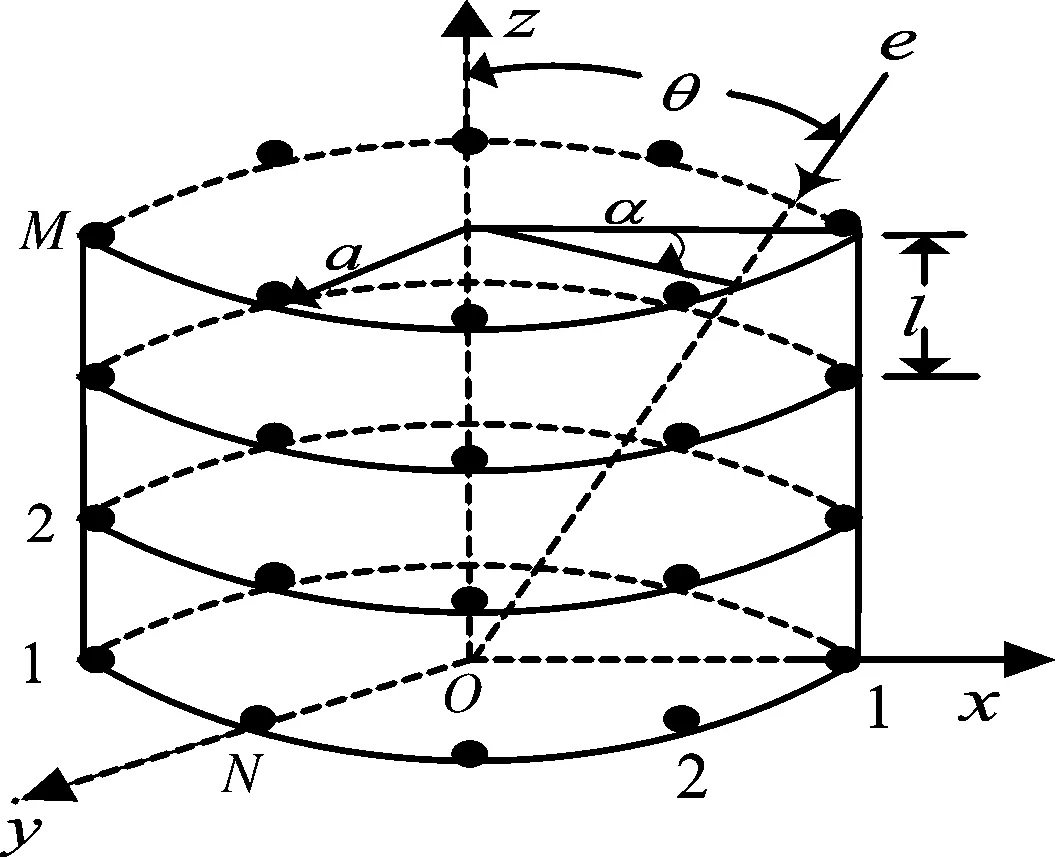
图3　线列阵组合圆周阵结构示意图

l为各圆周沿z轴方向的垂直距离，沿z轴方向可视为线列阵，线列阵指向性函数由式(1)可知，把每个圆周阵列看作为一级子阵，沿z轴方向的线阵列看作为二级子阵。根据乘积定理，其指向性函数为

D4(α,θ,ω)=D1(α,θ,ω)D3(α,θ,ω)。

(5)

1.5圆环形阵元阵列指向性函数

单个圆环形换能器的指向性函数[3]为

D5(α,θ,ω)=

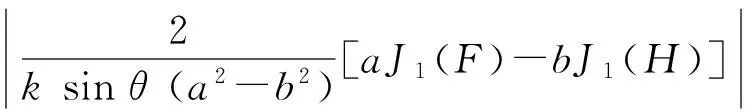
(6)

其中

F=kasinθ，H=kbsinθ，

a和b分别表示圆环形换能器的外内半径，J1(x)为一阶贝塞尔函数。

由Bridge乘积定理可知，圆环形阵元构成的平面阵列的指向性函数

D(α,θ,ω)=D2(α,θ,ω)D5(α,θ,ω)，

(7)

圆环形阵元构成的线阵列组合圆周阵的指向性函数

D(α,θ,ω)=D5(α,θ,ω)D4(α,θ,ω)。

(8)

2指向性分析

把48个薄圆环压电换能器设计成不同的矩形阵列形式和线列阵组合圆周阵列形式，根据指向性函数对其指向性进行Matlab仿真。

2.1矩形形式阵列

48个薄圆环压电换能器分别设计为2行24列、3行16列、4行12列、6行8列、7行7列(中心少一个换能器)以及8行6列的矩形形式阵列，即分别与2×24，3×16，4×12，6×8，7×7-1和8×6一一对应，其中所选换能器的内外半径分别为3 mm和5 mm，声波波长λ=7 mm。指向性仿真结果分别如图4、图5和图6所示。

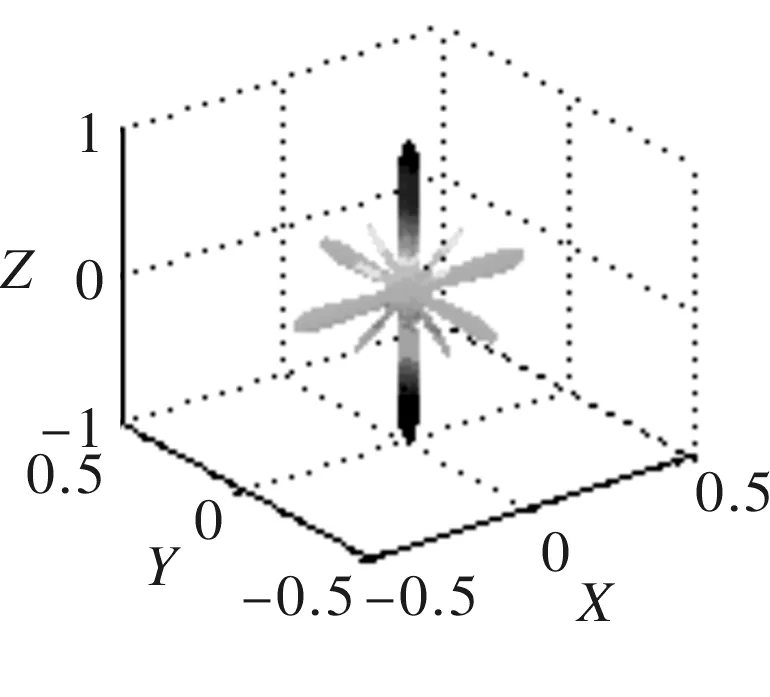
(a) 三维指向性(b)XY面指向性投影

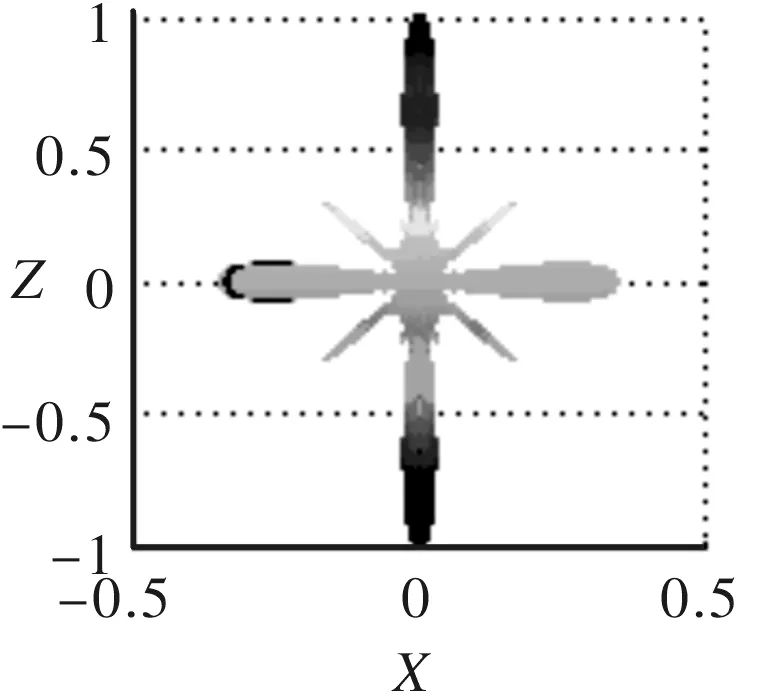
(c)XZ面指向性投影 (d)XZ面指向性投影

图48×6阵列指向性

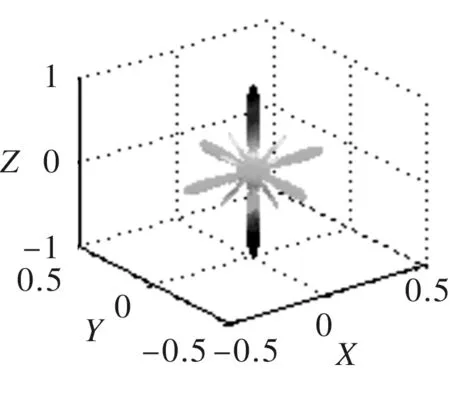
(a) 三维指向性(b)XY面指向性投影

(c)XZ面指向性投影(d)XZ面指向性投影

图56×8阵列指向性

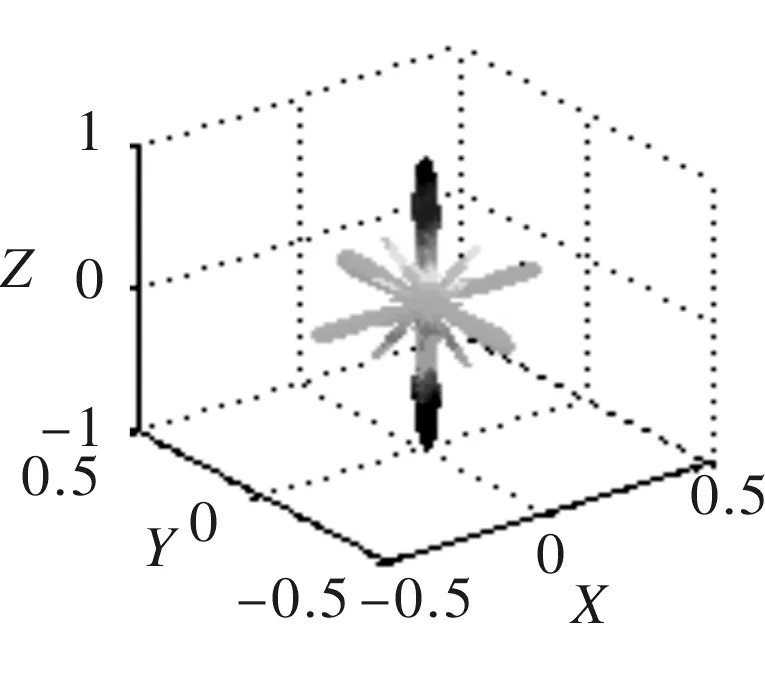
(a) 三维指向性(b)XY面指向性投影

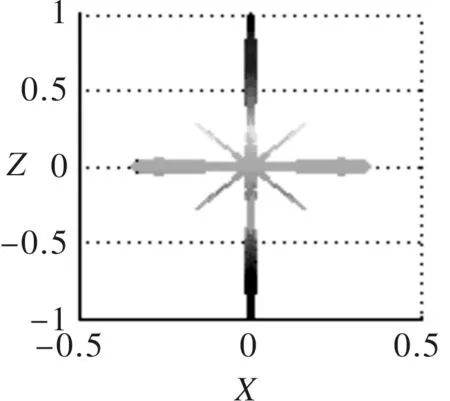
(c)XZ面指向性投影(d)XZ面指向性投影

图64×12阵列指向性

三维指向性图可以准确地反应出整个空间中主瓣和旁瓣的分布状况，由图4、图5和图6可以看出，矩阵形式阵列其指向性主瓣在空间中呈纺锤状，在平行于xOy面的横截面为椭圆形；在xOz定向面内，随着阵列列数的增加，主瓣宽度逐渐变窄，旁瓣幅值也得到了有效的抑制，指向性变好；在yOz定向面内，随着阵列行数的减少，指向性主瓣宽度逐渐变大，出现了较多的旁瓣和栅瓣，指向性变差。随着矩形阵列行列数差值的增大，三维指向性图变得越来越扁。

对于8行6列的矩形形式阵列，取阵元间距d=14 mm为定值，波长依次取7 mm、6 mm、5 mm和4 mm，其仿真结果如图7所示。

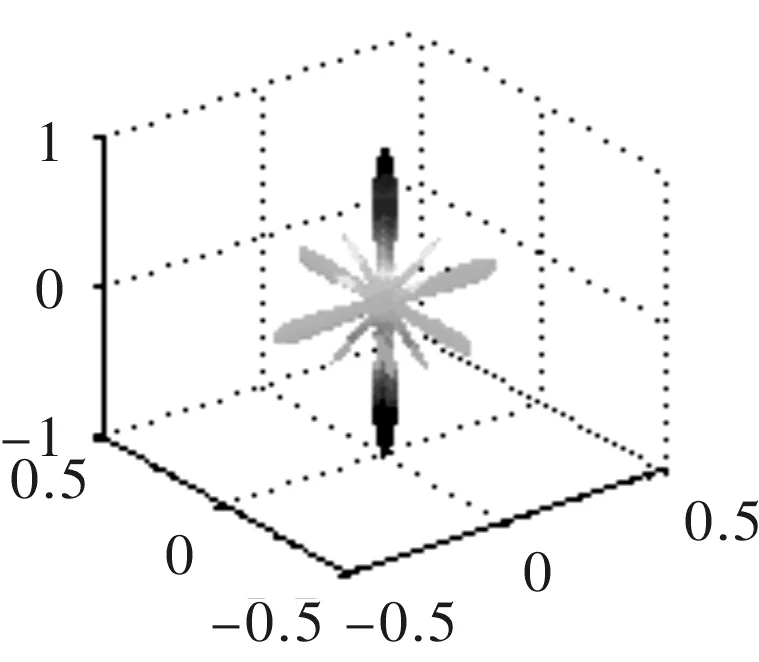
(a) λ=7 mm

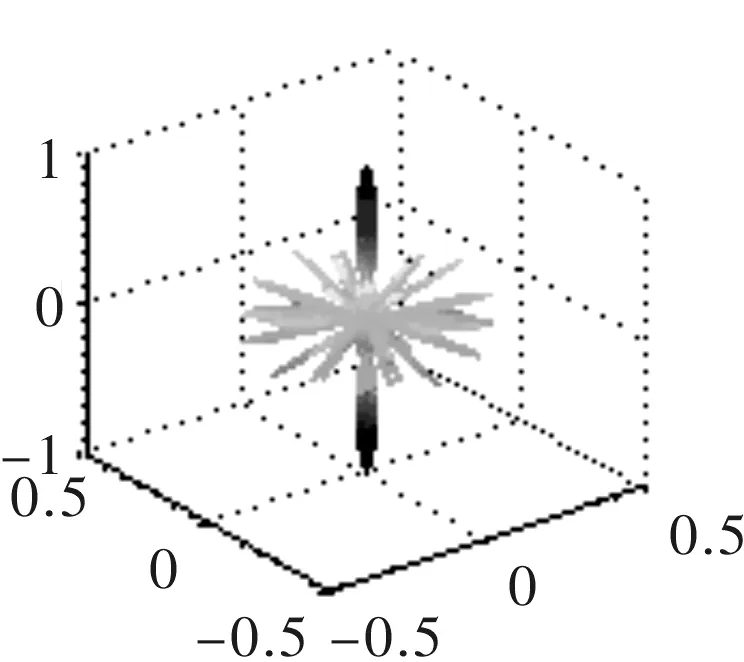
(b) λ=6 mm

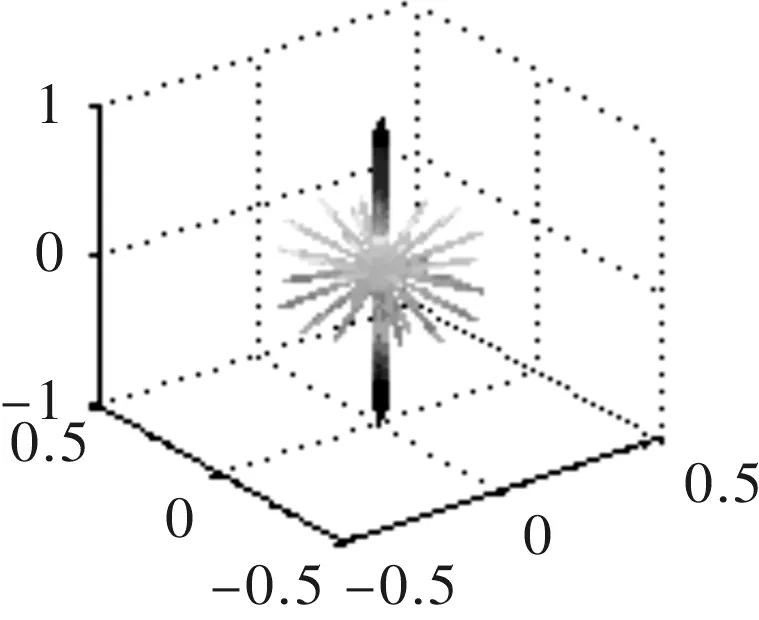
(c) λ=5 mm

(d) λ=4 mm

由图7可以看出,在一定的频率范围内，随着波长的减小，频率的增加，指向性主瓣宽度变窄，但是出现了较多的旁瓣，总体来说，指向性变好；超过一定的频率范围，主瓣变宽，旁瓣增多的同时幅值增大，指向性变差。

2.2线阵列组合圆周阵

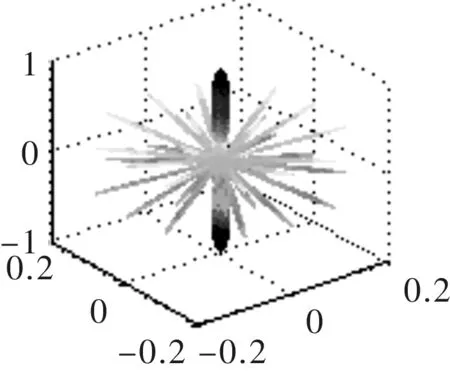
换能器大小尺寸不变，半径r=50 mm的圆周上均匀排列16个阵元，沿z轴方向均匀排列3层且各阵元在同一条直线上，各圆周阵之间的间距d=15 mm，波长λ=7 mm，其指向性仿真如图8所示。

由图8可知，线阵列组合圆周阵主瓣宽度明显变窄，虽然出现了较多的旁瓣，但旁瓣幅值大幅度减小，对主瓣的干扰性减弱，阵列指向性变好。

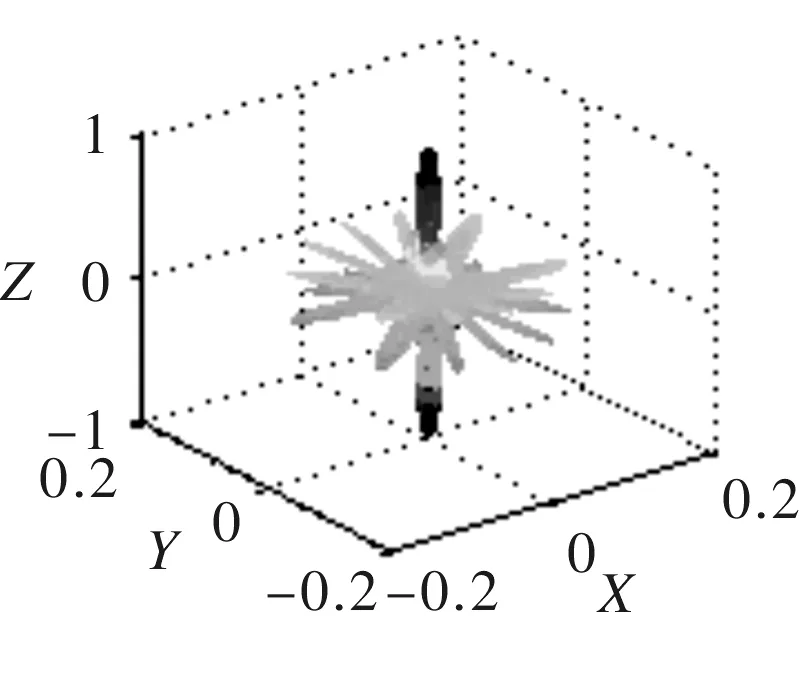
(a) 三维指向性

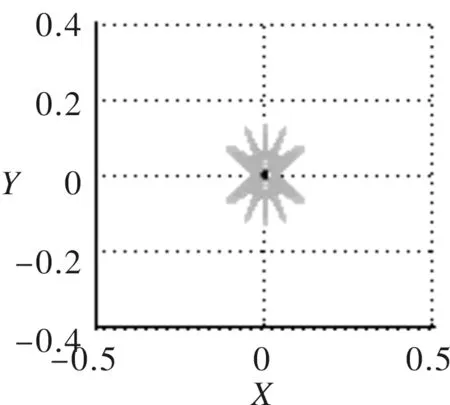
(b) XY面指向性投影

(c) XZ面指向性投影

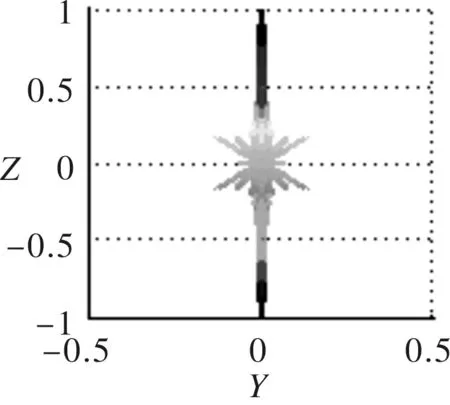
(d) XZ面指向性投影

3结束语

在薄圆环换能器尺寸、数目不变的情况下, 分别设计成不同的阵列, 对不同阵列指向性进行对比分析, 得到如下结论。

矩阵形式阵列，在行列各自对应的定向面内，随着行列阵元数量的增加，主瓣变窄，旁瓣得到了有效的抑制，指向性变好；行数和列数差值的增大，主瓣逐渐变成扁平状，在某一个定向面内指向性变好，其他定向面指向性变得较差。同一阵列阵元间距不变，随着波长的减小，频率的增大，主瓣宽度变窄，指向性变好。

线阵列组合圆周阵，在阵元尺寸，声波频率一定时，和矩阵形式阵列相比较，主瓣变窄，旁瓣幅值明显减小，指向性变好，虽然结构上比较复杂,但其具有实际的意义,可应用于实际的声学领域中。

参考文献

[1]杨天文, 陈敏，黄大贵，等.换能器阵列形式对指向性的影响[J].压电与声光,2014，36(1)：93-96.

[2]曹辉,张吉伟,白钧元.圆环形活塞声源的辐射阻抗[J]. 西北大学学报:自然科学版， 2014，44(1)：37-40.

[3]巩建辉,严碧歌.基于不同阵元换能器阵列的指向性研究[J].西北师范大学学报:自然科学版,2011,47(3):35-39.

[4]黄晶, 周社育, 阙沛文.线形超声相控换能器阵列的参数优化[J].压电与声光,2010,32(1):51-54.

[5]姚旭, 郭建中.线阵阵元间距和宽度对波束指向性的影响[J].陕西师范大学学报:自然科学版,2010, 38(1):46-50.

[6]李冬方.基于矢量水听器的圆柱阵波束形成方法[D].哈尔滨:哈尔滨工程大学,2013.

[7]杜功焕, 朱哲民, 龚秀芬.声学基础[M].南京:南京大学出版社, 2001 :344-348.

[8]郑贤中, 王秉.利用阵元异化振幅优化超声传感器阵列的指向性[J].传感技术学报, 2008, 21(5):761-764.

[9]栾桂东,张金铎,王仁乾.压电换能器和换能器阵[M].北京:北京大学出版社,2005 :352-364.

[10]李锦, 任中杰, 林书玉.环状活塞换能器辐射声场研究[J].陕西师范大学学报:自然科学版, 2003,31(4):28-29.

[11]陈敏, 徐利梅, 黄大贵, 等.基于MATLAB 换能器阵列指向性的分析研究[J].电声技术, 2006,26(5):25-28.

[12]常巍, 谢光军, 黄朝峰.MATLAB R2007 基础与提高[M].北京:电子工业出版社, 2007:165-196.

[责任编辑：祝剑]

Annulus piston transducer element array of three-dimensional directivity

FA Lin1，WANG Jun2，HAN Yonglan1，ZHAO Jie1，LIU Shipeng1

(1.School of Communication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China;2.School of Electronic Engineering,Xi’an University of Posts andTelecommunications,Xi’an 710121,China)

Abstract:According to the theory of transducer array directivity, the circular array is discussed. A numerical approach is borrowed to dissect the directivity of different matrix form arrays and line combinative circular arrays, which are all devised from 48 thin ring transducers. Simulation results show that, directivity difference of matrix form array will increase with the length-width ratio, the directivity of the same matrix form array will become better with the rise of frequency of acoustic wave, while, the line combinative circular array reaches a minimum sidelobe amplitude and a optimal directivity.

Keywords:directivity，matrix form array，line combination circular array，three-dimensional simulation

doi:10.13682/j.issn.2095-6533.2016.01.013

收稿日期：2015-07-28

基金项目：国家自然科学基金资助项目(40974078)

作者简介：法林(1955-)，男，教授，从事声学地球物理探测及信号处理研究。E-mail:fa_yy@yahoo.com.cn 王军(1989-),男，硕士研究生，研究方向为声光电交叉学科理论及其应用。E-mail: 411791449@qq.com

中图分类号：O424

文献标识码：A

文章编号：2095-6533(2016)01-0068-04