锂离子电池特征时间常数的理论提取及仿真

冯雅楠 黄秋安

摘 要：电化学阻抗谱是应用于锂离子电池的一种频率域测量方法，该方法能够获得丰富的物理化学信息，但由于频域混叠导致很多不同的物理过程表现出相同的阻抗谱特性。因此，通过从阻抗谱中提取特征时间常数来分辨对应物理过程很重要。文章从经典的锂离子电池等效电路模型入手，通过理论计算推导出特征时间常数分布函数解析表达式，然后利用Matlab仿真软件编写程序来检验该表达式的准确性，检验结果表明该表达式正确的反映了特征时间常数的分布情况。

关键词：锂离子电池；电化学阻抗谱；特征时间常数；仿真

中图分类号：TM910 文献标识码：A 文章编号：2095-1302（2016）06-00-03

0 引 言

随着全球能源生产与能源消费保持持续增长，能源结构也逐渐从化石能源向清洁能源转变。其中电能以它优越的清洁性、方便性和友好性成为了最大受益者。随着锂离子电池实现商品化应用以来，它在便携式电子设备如移动电话、笔记本电脑、数码相机等产品中获得了广泛的应用，而且有望在电动汽车、混合动力汽车、军事和航天等领域获得进一步的应用，是目前最为先进的一种绿色二次电池。

电化学阻抗谱（EIS）是研究电极系统的一种频率域测量方法[1，2]，可测定的频率范围很宽，因而可以比常规电化学方法得到更多的动力学信息和电极界面结构信息。但是由于EIS方法测量的数据中包含了大量的物理化学信息，这些信息由于频域混叠很难分离开，因此不能对该电极系统各性能参数进行准确的分析判断，从而影响对锂电池的性能分析。

为了更好地分析锂电子电池的各项性能，本文从经典的锂离子电池等效电路模型入手，通过理论计算推导出特征时间常数分布函数（DRT）解析表达式，并利用Matlab仿真软件编写程序检验了该表达式的准确性，检验结果表明该表达式正确地反映了特征时间常数的分布情况。

1 锂离子电池阻抗谱特性

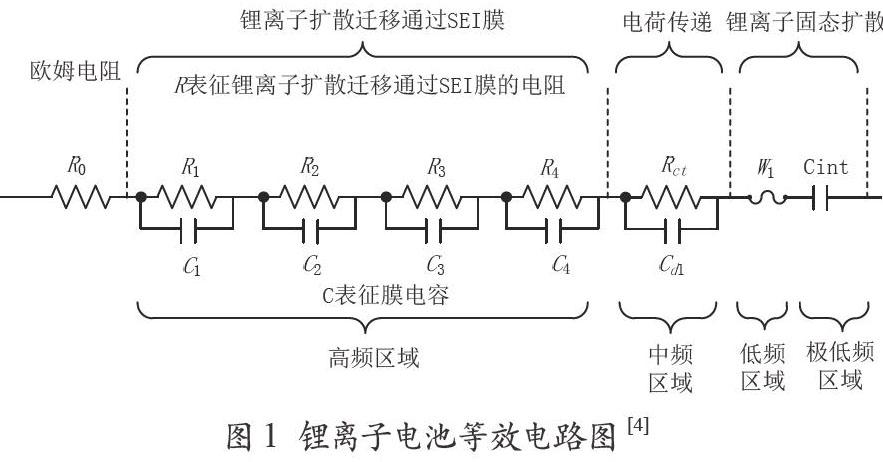
EIS在早期的电化学文献中称为交流阻抗。其测量方式是用一个角频率为ω的振幅足够小的正弦波电流信号对一个稳定的电极系统进行扰动时，相应的电极电位就做出角频率为ω的正弦波，从被测电极与参比电极之间输出一个角频率是ω的电压信号，测量的电压信号与电流信号的比值（此比值即为系统的阻抗）随正弦波频率ω的变化，或者是阻抗的相位角Φ随ω的变化，此时电极系统的频响函数就是电化学阻抗。电化学阻抗谱是指在一系列不同角频率下测得的一组这种频响函数值[3]。根据锂离子电池中锂离子在电解液中的扩散、锂离子通过多层SEI膜的扩散迁移、电荷传递、锂离子在活性材料中的固态扩散以及锂离子在活性材料中的累积和消耗，其等效电路图如图1所示[4]。

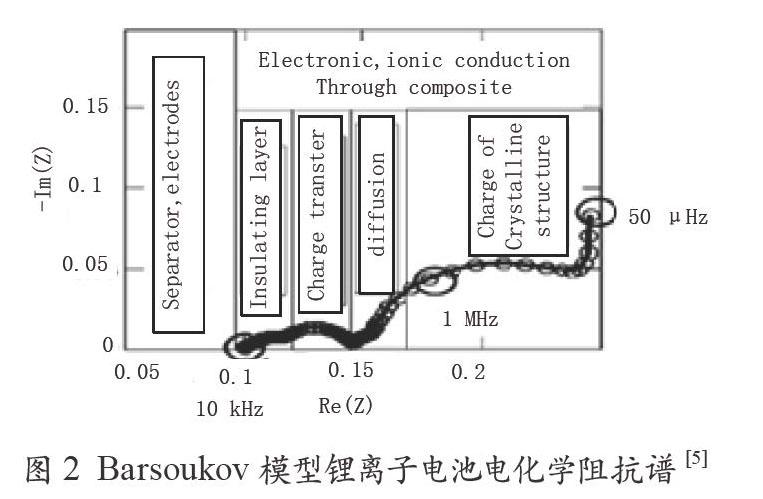
根据Barsoukov等[5]提出的锂离子电池的电化学模型，锂离子电池的典型EIS谱包括5个部分（如图2所示）：

（1）超高频区域（10 kHz以上），在EIS谱上表现为一个点；

（2）高频区域是与锂离子通过活性材料颗粒表面绝缘层的扩散迁移有关的一个半圆；

（3）中频区域是与电荷传递过程相关的一个半圆；

（4）低频区域，与锂离子在活性材料颗粒内部的固体扩散过程相关的一条斜线；

（5）极低频区域（<0.01 Hz），与活性材料颗粒晶体结构的改变或新相的生成相关的一个半圆以及锂离子在活性材料中的累积和消耗相关的一条垂线组成。

2 DRT理论推导

锂离子电池电化学阻抗谱的特征时间常数，可以反应电池有几个弛豫过程，它们变化速度的快慢对于探讨电极反应的机理是很有用的。对于从观察到的阻抗谱数据中提取时间常数分布的方法，在一些重要的专著[6，7]中已有很好的综述。但这些方法所得的数据并不准确，本文通过积分变换，将卷积方程与阻抗谱函数的分布函数联系起来。

2.1 时间常数分布函数

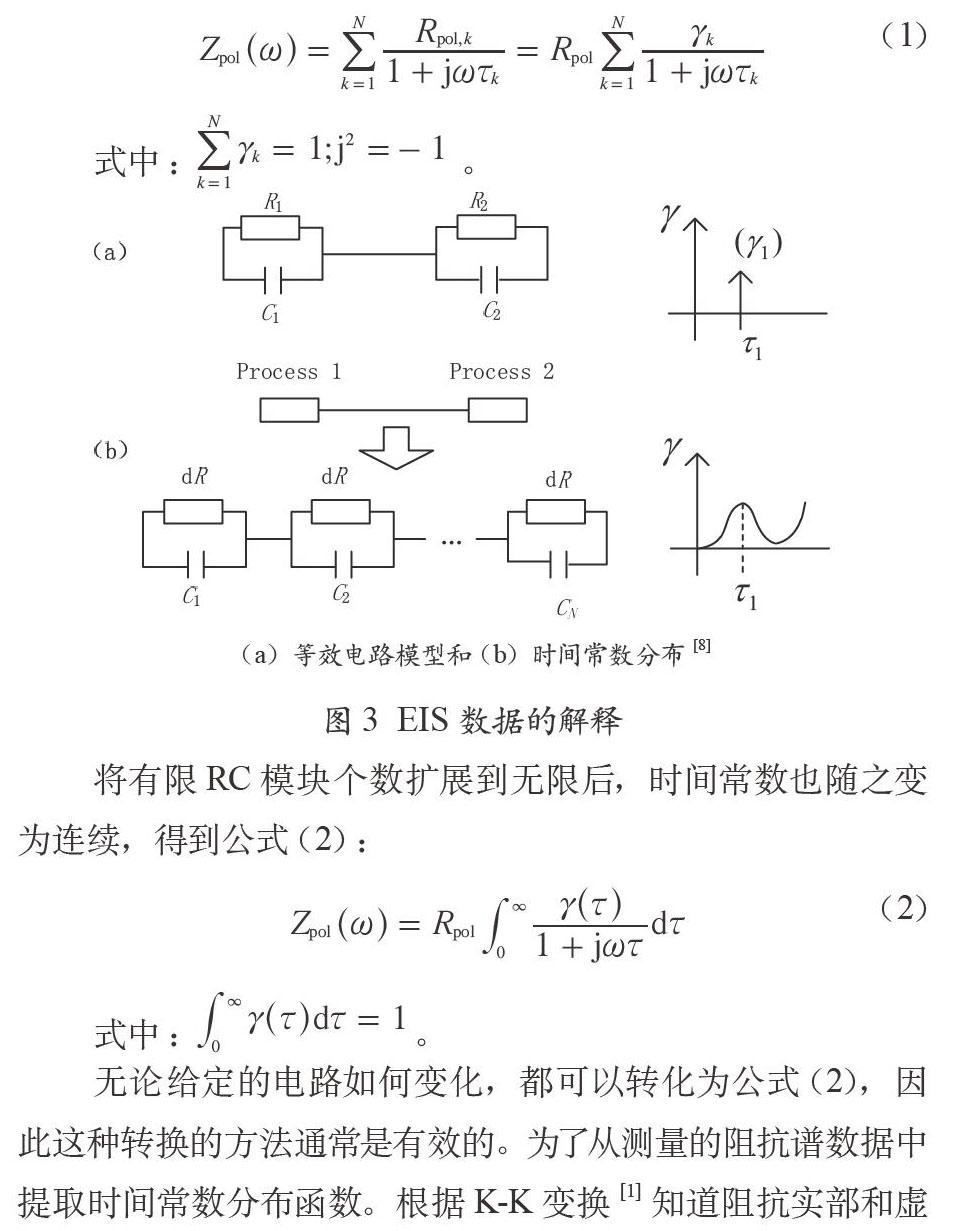
电化学系统的极化过程通常采用一个简单的等效电路模型，描述如图3（a）所示，即欧姆电阻并联电容为一个小模块，再将这些模块串联。在这种等效电路模型下，时间常数τ1=R1C1，τ2=R2C2。

通过峰值表示该动态过程的分布，在理想情况下峰值表示为时间常数对应的狄拉克脉冲函数，而实际的极化过程如图3（b）所示，峰值表示的是以一个主要时间常数为中心的封闭区域。以图3（b）中的模型为基础，令第k个RC模块的欧姆电阻Rpol，k为总极化电阻Rpol的γκ倍，即Rpol，κ=γκRpol，同时τκ表示该模块的时间常数[8]。则极化阻抗Zpol（ω）的表达式为：

由数据设置可以算出：w1=0.000 01、w2=0.001、w3=10、w4=0.1，则lnτ1=-5、lnτ2=-3、lnτ3=-3.6、lnτ4=-3.7。

根据理论推导利用Matlab计算得到的结果如图6所示。由图6可知，四个峰值位置分别在-1、1、3、5处。Matlab仿真结果与计算结果相吻合，仿真结果表明公式（9）正确地反映了特征时间常数的分布情况。

4 结 语

本文首先通过从经典的锂离子电池等效电路模型入手，推导出了锂离子电池电化学阻抗谱的特征时间常数的解析表达式，从理论上证明了特征时间常数分布函数的存在性。然后利用Matlab仿真软件来检验该表达式的准确性，仿真结果表明该表达式正确地反映了特征时间常数的分布情况。该结果同时也为数值提取电化学阻抗谱的特征时间常数提供了指导依据，进而对分析锂离子电池的特征时间常数与电极反应机理的内在联系提供理论依据，对锂离子电池电极系统的研究具有重要意义。

参考文献

[1]查全性.电极过程动力学导论[M].北京：科学出版社，1976.

[2]田昭武.电化学研究方法[M].北京：科学出版社，1984.

[3]曹楚南，张鉴清.电化学阻抗谱导论[M].北京：科学出版社，2002.

[4]庄全超，徐守冬，邱祥云，等.锂离子电池的电化学阻抗谱分析[J].化学进展，2010，22（6）：1044-1057.

[5] BarsoukovE.，KimD.H.，Lee H.S，et al.Comparison of kinetic properties of LiCoO2 and LiTi0.05Mg0.05Ni0.7Co0.2O2 by impedance spectroscopy[J].Solid State Ionics，2003，161（1）：19-29.

[6] MisellD.L.，Sheppard R.J.The application of deconvolution techniques to dielectric data[J]. Journal of Physics. D： Applied Physics，1973，6（4）：379-389.

[7] A.D.Franklin，H.J.DeBruin. The fourier analysis of impedance spectra for electroded solid electrolytes[J]. Physica Status Solidi.C，1983，75（2）：647-656.

[8] H.Schichlein，A.C.Müller，E.Ivers-Tiffée.Deconvolution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells[J]. Journal of Applied Electrochemistry，2002，32：875-882.

[9] H.Schichlein，A.Müller，E.Ivers-Tiffée. System：Anew modeling approach for SOFC single cells[Z].Solid Oxide Fuel Cells VI，Electrochem. Soc. Proc. Ser. 1999：1069-1077.

[10]陈戈珩，付虹，于德海.信号与系统实用教程[M].北京：清华大学出版社，2015

[11]高西全，丁美玉.数字信号处理[M].西安：西安电子科技大学出版社，2008.