基于模糊时间序列的车辆检测器数据修补方法研究
2016-06-30隆忠华王祥
隆忠华+王祥
摘 要:车辆检测器是交通管理中重要的数据采集工具,但在实际运用过程中,数据丢失问题往往影响其作用的发挥。本研究旨在建立一个可实用于交通控制中心的车检器缺失数据修补模型,尝试以不同模型来预测并修补车辆检测器缺失的数据,并对比各种模型的修补效果。文中提出了以ARIMA结合模糊时间序列的交通流量预测方法以及使用ARIMA进行短时间实时修补的方法,并获得了不错的效果。
关键词:交通流量预测;ARIMA;模糊时间序列;车辆检测器
中图分类号:TP274 文献标识码:A 文章编号:2095-1302(2016)06-00-04
0 引 言
车辆检测器是交通管理者掌握道路交通运行状况的重要工具。但是,在实际运用过程中,车辆检测器常因环境、维护、性能等原因发生数据丢失的现象。车辆检测器数据的丢失使得基于其所产生的控制和决策方案产生偏差甚至失效,无法彰显投资车辆检测器的应用价值。车检器数据修补算法是辅助提高车检器检测稳定性与准确性的途径之一。
本研究利用时间序列以及模糊时间序列的相关理论,根据交通流运行特征在工作日和假日的差异将车检器数据分成工作日和假日两种模式进行预测分析,使其能够对短时间内缺失的数据进行及时修补。并对比时间序列以及模糊时间序列两种方式进行数据修复的效果差异。
1 模型建立
数据为西安绕城高速单台车检器2014年全年数据,数据接收频率为每5分钟一次,理论上一天共288条数据记录。
1.1 数据预处理
数据预处理分为如下几项:
(1)首先将数据分为工作日和假日两种模式,再分别以ARIMA、混合模式以及传统平均法进行修补效率的比较。
(2)因车检器数据常发生缺漏和异常值,本研究采用6sigma理论对数据进行离群值判定,即先计算同一模式(工作日、假日模式)下同一时刻流量均值,将平均值正负6倍标准差范围外的流量数据判为异常值。
(3)本研究将进行ARIMA即时动态修补,以t-1时数据来预测t时的流量,持续验证峰值1小时内12条记录并计算绝对平均误差(MAPE)。
(4)本研究所使用的ARIMA模型由SPSS18.0建立,模糊时间序列由Matlab编写而成。
(5)模型以2/3的真实数据来建立(采用车检器2014年1~9月数据,剩下10~12月数据用来验证模式的准确性)。
1.2 ARIMA的建立
本研究使用SPSS18.0的ARIMA预测模型,将西安绕城高速车检器2014年1月1日至8月31日的流量数据切分为工作日与假日两种模式,具体研究步骤如下:
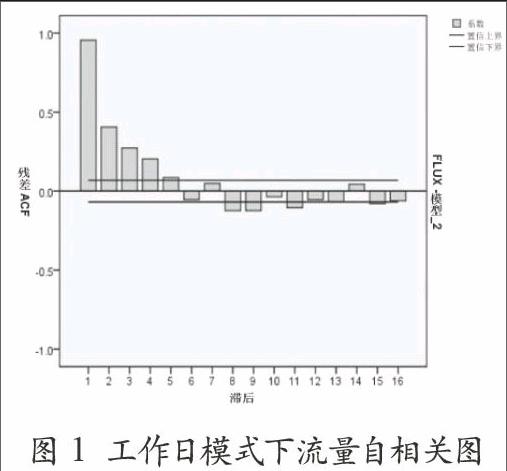
(1)利用自相关图(ACF)来判断是否为平稳数列。
(2)图 1所示为工作日模式下交通流量的自相关图,由图可见,滞后阶数为5时,才进入置信界内,表示流量数据并非为一个平稳的时间序列,需要对数据进行差分处理。
图 2所示为假日模式下交通流量的自相关图,在其滞后阶数为7时才进入了置信界限内,数据亦需要差分处理。具体操作如下:
(1)使用SPSS18.0中的Expert Modeler选出最佳ARIMA(p,d,q)模型,工作日模式下的最佳ARIMA(p,d,q)模型为ARIMA(0,1,1),假日模式下的最佳模型是ARIMA(1,1,1)。
(2)检查模型的R2与MAPE值是否能够充分解释变异数,BIC值是否最低并且残差是否符合白噪声的假设。
依照统计学的衡量标准,MAPE值小于20%时为优良的修补模型,而模型的BIC值则越小越好;R2表示模型的解释程度,R2值越高则解释变数的能力越高,表1所列为工作日模式的挑选准则,可以看出由Expert Modeler所得的模型四项准则皆为最优,比较的模型为符合残差接收白噪声假设的模型,其MAPE值为16.91%(越低越好),是三个模型里最好的,R2=0.938是最高的,代表可解释变数的程度最高,BIC值越小表示模型为最佳估计模型,其BIC值=4.92为三个模型中最低。而表2所示为假日模式的挑选准则,同样是由Expert Modeler挑选出最适模型为最优模型,ARIMA(1,1,1)各个适合度指标皆为最适,也都有符合残差接收白噪声,由此可知,可直接由Expert Modeler选取ARIMA的最适模型,不需要采用传统的方式将所有模型进行测试。
将建立好的工作日与假日流量ARIMA模型,选择输出一个完整日的流量数据来进行实际验证。工作日模式下ARIMA预测结果如图3所示。假日模式下ARIMA预测结果如图4所示。
1.3 结合模糊时间序列的ARIMA模型
首先建立一个将max-min简化的模糊时间序列模型,以车检器数据中9月1日17:00至19:00每5 min流量为例,预测一个小时的流量数据。示例流量数据表如表3所列。
(3)将时间分为24个子集合(A1、A2、…、A24)并计算各个集合的时间隶属度。
(4)使用加权平均法进行去模糊化计算。
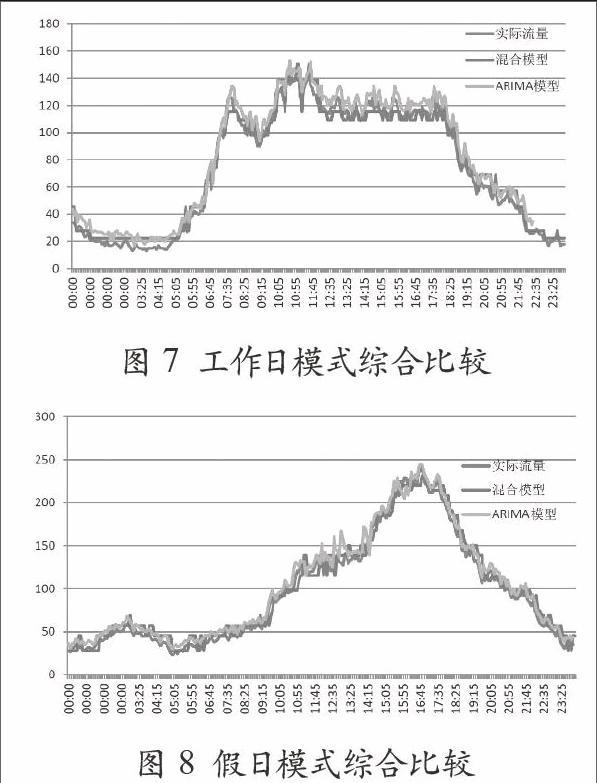
(5)将工作日模式与假日模式下的ARIMA预测值与模糊时间序列的计算结果进行对比。工作日模式下ARIMA的MAPE值为16.907%,而工作日模式下混合模型的MAPE值为13.248%,对比可知混合模型效果较好。基于差分平稳化方法,本研究先以ARIMA模型使其收敛,这样能够比单使用ARIMA模型的效果好,而假日混合模型的MAPE值为10.698%,同样优于假日ARIMA模型的17.145%。可以发现假日模式的改善比工作日模式的改善幅度大,这种现象可以解释为工作日的流量变化较大,为一个双峰M型分布,而假日的流量图形基本为一个单峰分配,变化不剧烈,较符合模糊时间序列的梯度函数形态。工作日混合模式的函数形态如图5所示。假日混合模式的函数形态如图6所示。
