基于强度包络理论的混凝土疲劳剩余强度计算模型

刘芳平，周建庭

(1.重庆三峡学院　土木工程学院，重庆　404000;2.重庆交通大学　土木工程学院，重庆　400074)

基于强度包络理论的混凝土疲劳剩余强度计算模型

刘芳平1,2，周建庭2

(1.重庆三峡学院土木工程学院，重庆404000;2.重庆交通大学土木工程学院，重庆400074)

摘要：为了研究疲劳荷载作用下混凝土剩余强度退化规律，基于强度包络理论，推导了混凝土经历任意次数疲劳加载后的剩余强度包络线方程，建立了任意次数疲劳加载后的混凝土剩余强度计算模型，并用试验进行了验证分析。研究结果表明：模型假设的疲劳破坏判据正确，选择的剩余强度包络线合理；计算结果符合混凝土剩余强度退化规律并满足边界条件，模型能有效模拟混凝土在疲劳过程中的剩余强度退化规律；因引入线性损伤函数，模型计算的混凝土剩余强度退化规律更接近线性变化，而试验趋向于非线性变化，应力水平越低这种倾向性更明显；特定疲劳次数剩余强度计算值接近试验值，平均误差只有2%。

关键词：道路工程；疲劳剩余强度；包络理论；混凝土；强度计算模型

0引言

混凝土在使用中会承受循环荷载，在这些高频重复荷载下可能会在低于材料屈服或极限强度条件下产生疲劳破坏，或虽未发生疲劳破坏，但终会因剩余强度低于初始强度造成安全隐患。因此，研究混凝土材料疲劳强度耗散十分重要。国内外大量学者对混凝土等复合材料剩余强度的衰减规律提出了自己的表达式。顾怡、姚卫星[1]提出了疲劳加载下纤维复合材料的剩余强度；顾怡[2]提出了复合材料拉伸剩余强度及其分布；Hashin Z[3]根据试验假定的剩余强度初始退化率，并做一般化处理后给出了剩余强度退化模型；冯培锋等[4]根据刚度建立了剩余强度模型；Chou P C等人[5]做出了强度-寿命等效秩假设，建立了剩余强度模型；孟宪宏[6-7]基于连续体损伤力学理论建立混凝土抗压疲劳剩余强度随疲劳次数衰减的模型，又在Schaff[8]等人研究基础上建立了混凝土剩余强度随疲劳次数衰减的模型。Reifsnider[9]讨论了剩余强度与静强度的关系。以上这些模型大多形式复杂，参数较多，试验较少，能提供给模型确定其中参数的试验数据非常有限，研究中不宜选用。对这些模型分析发现表达式虽各有不同，但一般都符合剩余强度理论的如下边界条件。

(1)σr(0)=σ0， 即材料强度初始值为未加载时的强度，一般σ0取材料的强度极限σb。

(2)σr(Nf)=σmax， 即材料达到疲劳寿命Nf破坏时，剩余强度等于疲劳载荷峰值。

(3)临近破坏，强度突然下降，即出现σr(n)“突然死亡”行为，且dσr(n)/n≤0，d2σr(n)/n2<0。

基于以上分析，本文在分析混凝土疲劳剩余强度退化规律及边界条件基础上，从材料剩余强度衰减的整体过程出发，求解任意次数疲劳加载后混凝土剩余强度与加载次数之间的关系曲线，即通过混凝土疲劳剩余强度包络线来研究混凝土疲劳剩余强度，并用试验数据对建立的模型进行验证。

1混凝土剩余强度包络线确定

1.1确定包络线曲线形状

文献[10]研究认为混凝土在拉、压疲劳荷载作用下破坏时的最大总应变与混凝土单轴加载软化阶段最大应力所对应的应变相当，如图1所示，文献[11]通过试验与模拟对上述研究结果进行了验证。其实从能量的角度讲混凝土疲劳过程与单调加载过程中的能量耗散是一样的，从而侧面也可以解释这一现象。

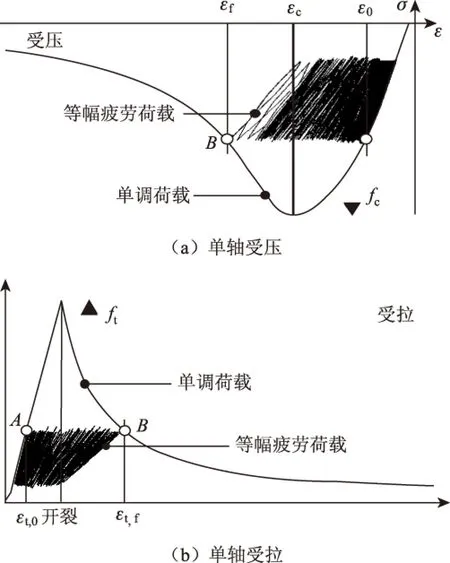
图1　混凝土单轴静载与疲劳过程的应力-应变曲线Fig.1　Stress-strain curves of concrete under uniaxial loading and fatigue process注：图中的A点为初始疲劳点；B点为混凝土单轴静载应力-应变曲线上疲劳破坏点。

从混凝土强度整体衰减规律看，混凝土在疲劳荷载作用下的应力-应变滞回曲线如图2所示，分析发现其包络线与单轴静载应力-应变模型软化段曲线非常接近，故本文用混凝土单调静载应力-应变曲线软化阶段最大应力所对应的应变作为疲劳破坏的依据，用混凝土单轴静载应力-应变模型软化段曲线来近似表示混凝土在疲劳破坏时的剩余强度包络线，如图3所示。

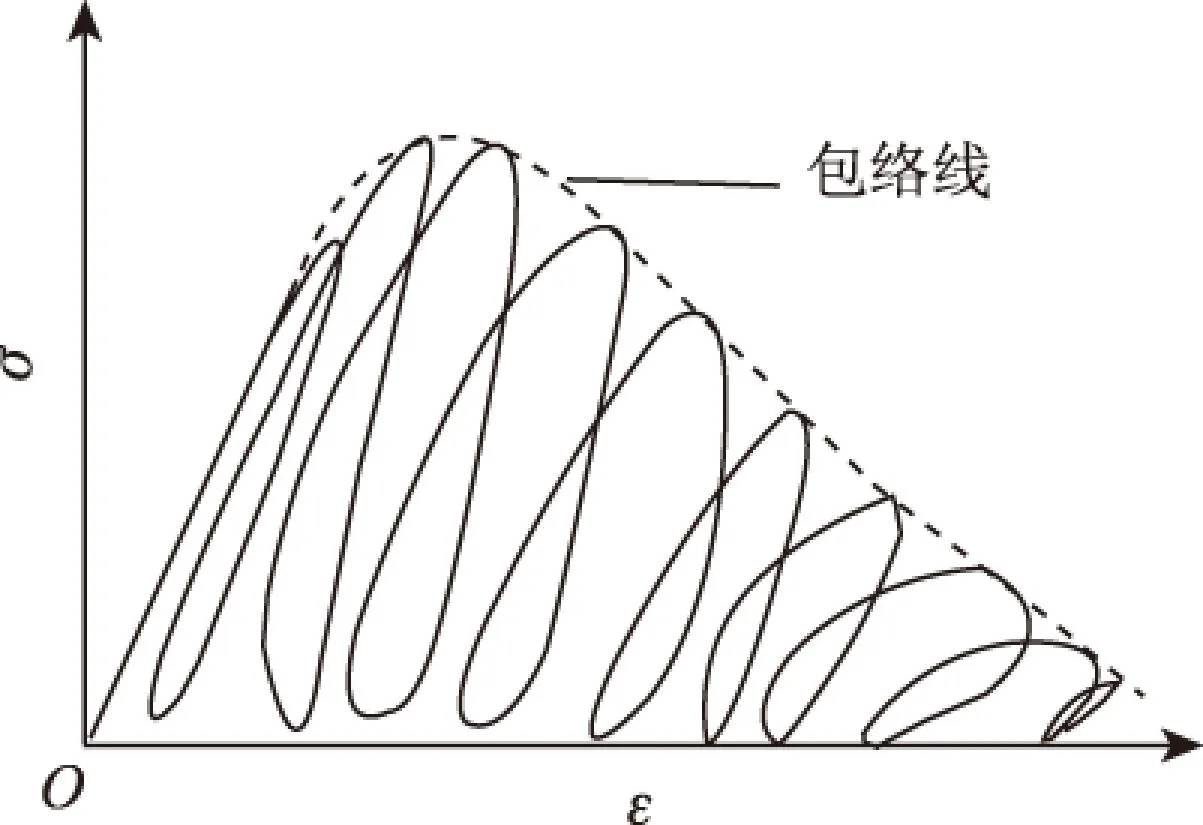
图2　混凝土循环应力应变滞回曲线Fig.2　Concrete cyclic stress-strain hysteresis curve

图3　混凝土疲劳剩余强度包络线Fig.3　Envelope of concrete fatigue residual strength

1.2求解剩余强度包络线方程

规范[12]得到的混凝土单轴受压与受拉应力-应变曲线下降段的方程见式(1)～(2)：

(1)

(2)

式(1)～(2)中：ε>εc,ε>εt,αc,αt分别为混凝土单轴受压与受拉应力-应变曲线下降段形状系数；fc,ft分别为混凝土单轴抗压与抗拉强度；εc,εt分别为fc与ft对应的峰值压、拉应变。

参照(1)～(2)方程的求解方法，并结合图3表示的混凝土疲劳剩余强度包络线，可得受压与受拉疲劳强度包络线方程见式(3)～(4)：

(3)

(4)

式中，σr,c(N) 与σr,t(N)分别为混凝土受到任意次数疲劳加载后破坏的受压与受拉剩余强度；x(N) 为疲劳加载次数N有关函数；

2混凝土疲劳剩余强度计算模型

由式(3)～(4)求得混凝土经过任意次数疲劳加载后的剩余强度为：

(5)

对函数x(N)分析发现满足以下边界条件：

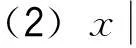
故本文引入满足边界条件(1)、(2)且与线性损伤理论一致的函数x(N)如下：

(6)

(7)

求解方程(7)得到混凝土受压时x(Nf)为：

(8)

同理，根据受拉疲劳边界条件与方程(4)，得到混凝土受拉疲劳时x(Nf)的方程为：

(9)

求解方程(9)可得到混凝土受拉时x(Nf)。

综上所述，将式(6)代入式(5)可求得混凝土经历任意次数疲劳加载后剩余强度为：

(10)

式(10)即为混凝土在疲劳荷载作用下的剩余强度计算模型。

3模型验证

本文用孟宪宏[7]试验数据对混凝土经历任意次数疲劳加载后的剩余强度式(10)进行验证。孟宪宏分别做了7组混凝土强度为C30的抗压与抗拉试件，其中第1组测试混凝土静力抗压(抗拉)强度；第2组与第5组10个(抗拉为12个)试件测试最大应力水平在0.75fc和0.85fc(抗拉时为0.75ft和0.85ft)时混凝土疲劳寿命；第3组与第4组12个(抗拉为15个)试件测试混凝土最大应力水平为0.75fc(抗拉为0.75ft)时，分别疲劳1×104与2×104次数(抗拉为疲劳1×104与1.5×104次)后混凝土剩余强度；第6组与第7组12个(抗拉为15个)试件测试混凝土在最大应力水平为0.85fc(抗拉为0.85ft)时，分别疲劳5×102与1×103次数(抗拉为疲劳103与2×103次)后混凝土的剩余强度。为了减少试件测量结果的离散性，增加准确性，本文将每组试件试验结果进行平均，试验数据平均值见表1。

表1　混凝土疲劳剩余强度试验结果

注：①试验数据来自孟宪宏，本文取为各组试件平均值；

②σ0,σr分别为初始强度与剩余强度。

本文式(10)计算过程中，先由式(8)计算在最大应力水平为0.75fc=18.352 5 MPa与 0.85fc=20.799 5 MPa下的x(Nf)值分别为1.632 7，1.436 6。混凝土抗压初始强度σ0取用表1中试验平均值，即24.47 MPa，C30混凝土单轴受拉应力-应变曲线下降段形状系数αc按规范[13]表C.2.4取值为1.36，计算的剩余强度退化规律见图4。

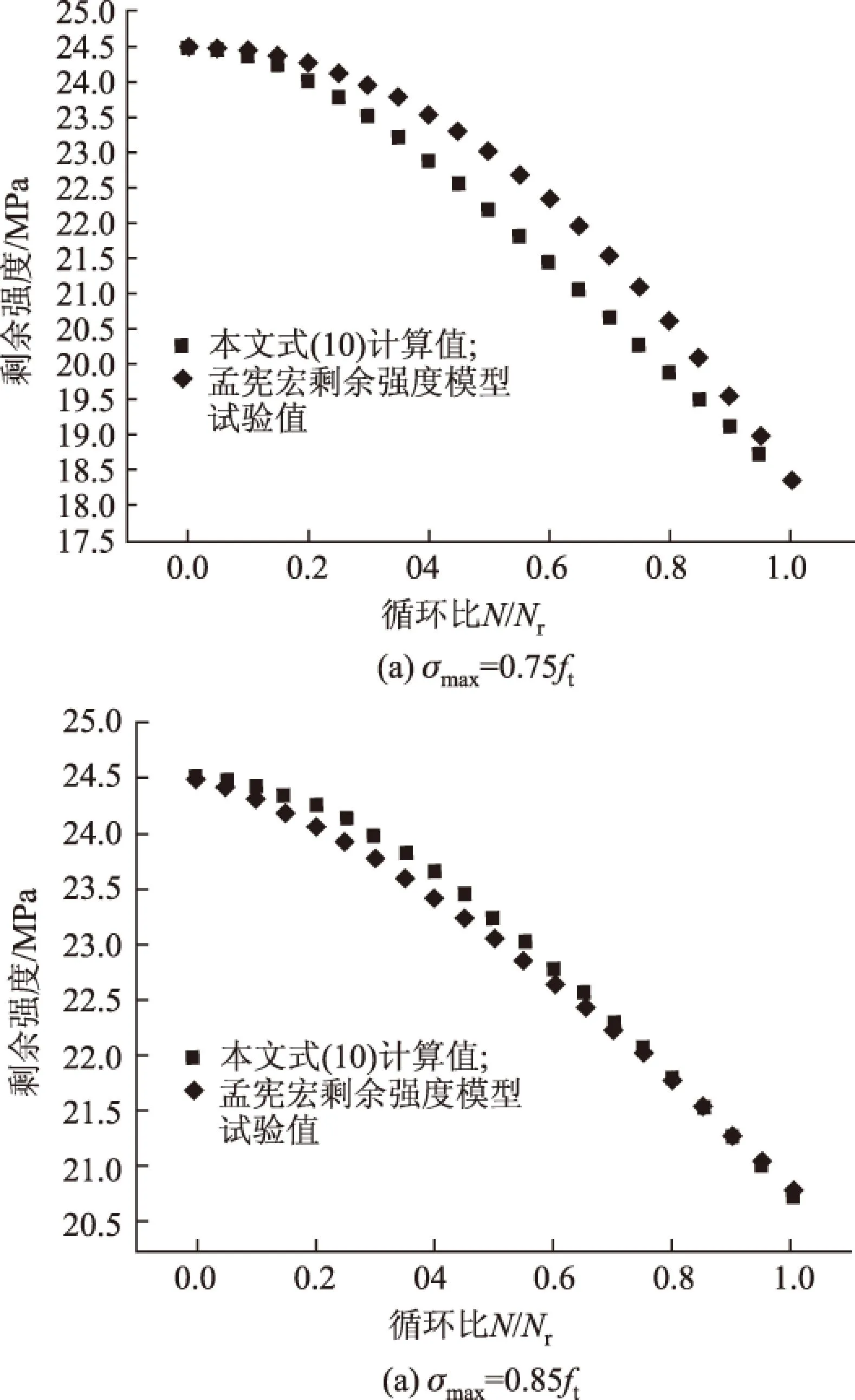
图4　混凝土抗压疲劳剩余强度退化规律Fig.4　Degeneration of concrete fatigue compressive residual strength

本文公式(10)计算过程中，由式(9)计算得到在最大应力水平0.75ft=2.019 MPa与0.85ft=2.288 2 MPa下的x(Nf)值分别为1.274 8，1.220 8。混凝土抗拉初始强度σ0取用表1中试验平均值，即2.692 MPa。C30混凝土单轴受拉应力-应变曲线下降段形状系数αt参照规范[12]表C.2.3取值为2.81，计算得到剩余强度退化规律见图5。

图4、图5看出，当循环次数为0时，混凝土强度都等于初始强度，即图4中的24.47 MPa，图5中的2.692 MPa；当循环次数达到疲劳寿命时，剩余强度衰减到疲劳荷载上限对应的应力，即图4(a)中的20.799 5 MPa，图4(b)中的18.352 5 MPa，图5(a)中的2.019 MPa，图5(b)中的2.282 2 MPa。计算结果与试验吻合，且都满足边界条件。从混凝土强度衰减的过程来看，符合混凝土剩余强度衰减一般规律，临近破坏，dσr(n)/n≤0，d2σr(n)/n2<0。

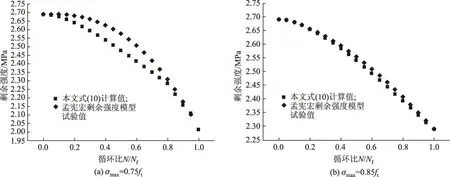
图5　混凝土抗拉疲劳剩余强度退化规律Fig.5　Degeneration of concrete fatigue tensile residual strength

本文计算结果和试验区别在于，计算退化规律更接近线性变化，而试验趋近于非线性，原因主要是本文引入的是满足边界条件且与线性损伤理论一致的函数x(N)，见式(6)，在实际中混凝土的疲劳损伤并非为完全线性损伤。文献[8]选用剩余强度衰减模型为：σr(n)=σr(0)-[σr(0)-σmax](n/Nf)ν， 只测试了特定疲劳次数下的剩余强度，如混凝土疲劳抗压强度中测试的为疲劳1×104与2×104次数后混凝土的剩余强度(0.75fc)与疲劳5×102与1×103次数后混凝土的剩余强度(0.85fc)，通过其确定公式中与应力水平有关的参数υ，再通过曲线拟合的方式得到混凝土强度衰减的规律，本身结果与真实强度退化规律有一定的差异。

本文将文献[7]试验中测得的特定疲劳次数剩余强度值和本文模型计算值进行了比较，如表2所示。从表2中数据看出，计算值与试验值(各组构件平均值)比较接近，平均误差只有2%左右。

表2　疲劳剩余强度计算值与试验值对比表

注：试验数据来自孟宪宏，本文取为各组试件平均值。

4结论

(1) 基于剩余强度理论的边界条件及强度包络理论，推导了混凝土经历任意次数疲劳加载后的剩余强度包络线方程，建立了任意次数疲劳加载后的混凝土剩余强度计算模型。对于由混凝土构成的受压、受拉与受弯等各种构件的疲劳损伤、疲劳刚度与强度以及疲劳承载力退化等问题的进一步求解，可在本文建立的剩余强度公式基础上进行。

(2)建立的模型计算结果符合混凝土剩余强度退化规律与满足边界条件，能有效模拟混凝土在疲劳过程中的剩余强度退化规律。因此，本文选择用混凝土单调静载应力-应变曲线软化段最大应力所对应的应变作为疲劳破坏判据正确，用软化段曲线来近似表示混凝土在疲劳破坏时的剩余强度包络线合理可行。

(3)计算模型得到的混凝土剩余强度接近线性变化，试验趋向于非线性变化，根本原因在于引入的函数x(N)以及试验数据的连续性。故以后研究中的关键是引入与混凝土实际损伤一致的函数x(N)，且试验中剩余强度试验点越多，得到的混凝土强度退化规律越贴近实际。

参考文献：

References:

[1]顾怡，姚卫星. 疲劳加载下纤维复合材料的剩余强度[J].复合材料学报，1999，16(3)：98-102.

GU Yi, YAO Wei-xing. Residual Strength of fiber Reinforced Plastics under Fatigue Loading[J]. Acta Materiae Compositae Sinica, 1999, 16( 3)：98-102.

[2]顾怡.复合材料拉伸剩余强度及其分布[J].南京航空航天大学学报,1999, 31(2):164-171.

GU Yi. A Model of Tensile Residual Strength of FRP and Its Distribution[J]. Journal of Nanjing University of Aeronautics & Astronautics, 1999, 31(2):164-171.

[3]HASHIN Z. Cumulative Damage Theory for Composite Materials：Residual Life and Residual Strength Methods [J]. Composites Science and Technology, 1985, 23(85):1-19.

[4]冯培锋，王殿富，杜善义，等. 复合材料层压基于剩余刚度比的剩余强度模型[J]. 应用力学学报，2001,18(1): 41-44.

FENG Pei-feng, WANG Dian-fu, DU Shan-yi, et al. A Fatigue Residual Strength Model for Composite Laminates Based on Residual Stiffness Ratio[J].Chinese Journal of Applied Mechanics, 2001, 18(1):41-44.

[5]CHOU P C, CROMAN R. Residual Strength in Fatigue Based on The Strength-life Equal Rank Assumption [J]. Journal of Composite Materials, 1978, 12(2):177-194.

[6]孟宪宏，宋玉普.混凝土抗压疲劳剩余强度损伤模型[J].沈阳建筑大学学报:自然科学版，2009,25(1):12-16.

MENG Xian-hong, SONG Yu-pu.Damage Model for the Residua Strength of Concrete under Compression Fatigue Loading[J]. Journal of Shenyang Jianzhu University:Natural Scienc，2009, 25(1):12-16.

[7]孟宪宏. 混凝土疲劳剩余强度试验及理论研究[D].大连:大连理工大学，2006.

MENG Xian-hong. Experimental and Theoretical Research on Residual Strength of Concrete under Fatigue Loading[D]. Dalian：Dalian University of Technology, 2006.

[8]SCHAFF J R, DAVIDSON B D. Life Prediction Methodology for Composite Structures. Part 1-Constant Amplitude and Two-stress Level Fatigue [J].Journal of Composite Materials, 1997, 31(2):128-157.

[9]REIFSNIDER K L, STINCHCOMB WW, O’BRIEN T K. Frequency Effects on A Stiffness-based Fatigue Failure Criterion in Flawed Composite Specimens [C]// Fatigue of Filamentary Composite Materials. Philadelphia: American Society for Testing and Materials, 1977:171-184.[10]KIM J K, KIM Y Y. Experimental Study of the Fatigue Behavior of High Strength Concrete [J].Cement and Concrete Research, 1996, 26(10): 1513 -1523.

[11]朱劲松, 宋玉普,肖汝诚. 混凝土疲劳特性与疲劳损伤后的等效单轴本构关系[J]. 建筑材料学报, 2005,8(5): 484-489.

ZHU Jin-song, SONG Yu-pu, XIAO Ru-cheng. Fatigue Behavior and Post-damaged Equivalent Constitutive Law of Plain Concrete [J]. Journal of Building Materials, 2005,8(5): 484-489.

[12]GB 50010—2010,混凝土结构设计规范[S].

GB 50010—2010, Code for Design of Concrete Structures [S].

Calculation Model of Concrete Fatigue Residual Strength Based on Strength Envelope Theory

LIU Fang-ping1,2，ZHOU Jian-ting1

(1. School of Civil Engineering, Chongqing Three Gorges University, Chongqing 404000, China;2. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

Abstract：In order to study the deterioration of the residual strength of concrete under fatigue loading, based on the strength envelope theory, the envelope equation of the residual strength of concrete after any cycles of fatigue loading is derived, and the calculation model of the residual strength is established, which is verified by a test. The result indicates that (1) the fatigue failure criterion of the model assumption is correct，the selected residual strength envelope is reasonable; (2) the calculation result is in line with the residual strength deterioration and meets the boundary conditions, the model can effectively simulate the deterioration of residual strength of concrete in fatigue process; (3) because of the introduced linear damage function, the model calculation result of the residual strength is close to linear change, but the test tends to nonlinear change, the lower the stress level the more apparent the tendency; (4) the calculation result of the residual strength in some certain fatigue cycle is close to the experimental values, the average error is only 2%.

Key words：road engineering；fatigue residual strength；envelope theory；concrete；strength calculation mode

收稿日期：2015-07-06

基金项目：国家自然科学基金项目(51278512)；重庆市教委科学技术研究项目(KJ1401024)；重庆三峡学院校级青年项目(15QN14)

作者简介：刘芳平(1981-)，男，甘肃陇西人，博士研究生.(LFP05270214@163.com)

doi:10.3969/j.issn.1002-0268.2016.06.002

中图分类号：U441.4

文献标识码：A

文章编号：1002-0268(2016)06-0009-06