大型地下洞室群相邻块体地震响应

李文倩,佟大威,王　振,朱晓斌,鲁文妍,2

(1. 天津大学水利工程仿真与安全国家重点实验室,天津　300072;2. 南京水利科学研究院材料结构研究所,江苏 南京　210029)

大型地下洞室群相邻块体地震响应

李文倩1,佟大威1,王振1,朱晓斌1,鲁文妍1,2

(1. 天津大学水利工程仿真与安全国家重点实验室,天津300072;2. 南京水利科学研究院材料结构研究所,江苏 南京210029)

摘要：为了更好地模拟地下洞室中存在的相邻块体结构在地震荷载作用下的运动与动态响应特性,建立了一种考虑块体间黏结强度影响的地下洞室相邻块体动力抗滑模型,并通过数值模型分析了该抗滑模型的有效性与优越性。在工程实例分析中,采用经典抗滑模型时Ⅰ类相邻块体中两块体水平X向位移在整个地震阶段的均方根值分别为2.16 cm和2.02 cm,采用修正抗滑模型时两块体对应响应值分别为2.00 cm和1.94 cm;Ⅱ类相邻块体中两块体在经典抗滑模型与修正抗滑模型条件下的对应响应值分别为3.68 cm和3.65 cm与3.55 cm和3.54 cm,上述结果反映了相邻块体在黏结特性的作用下具有更好的稳定性,说明该模型具有较好的工程适用性与应用价值。

关键词：地下洞室;相邻块体;黏结特性;抗滑模型;地震响应

大型水利工程地下洞室往往处于极端复杂的地质条件下,洞室周边分布的块体中既包括单一块体,也包括相邻块体,其中相邻块体结构在地震荷载激励下产生的动力响应特性是判断洞室稳定性的主要安全参量,也是评估水利工程结构整体安全性的重要指标。

针对大型地下洞室块体结构的动力特性模拟,不仅涉及结构所受地震荷载的激励特性,同时也需要考虑来自块体自身的动态稳定机理及其接触抗滑特性的影响。最早的岩体工程中块体与动接触理论由Goodman等[1-2]提出并得以广泛应用,石根华根据块体稳定分析的几何原理与岩体的影响因素建立了滑动体的数学模型并提出块体稳定分析方法。至今,考虑地下洞室块体结构动力特性的方法主要包括连续数值方法[4]、非连续数值方法[5-6]和耦合数值方法[7-10],这些方法多局限于单一块体的研究而对相邻块体在强震作用下的动态响应研究较少,同时现有理论与研究中往往只重视块体本身的动力性质而忽视岩体间黏结强度对接触面动态特性的影响效应,在解决实际工程问题上具有一定的局限性。

本文在研究相邻块体地震响应的基础上,考虑实际工程中裂隙结构面的不完整性与黏结性,建立了地下洞室相邻块体周边接触面动力抗滑模型,在理论上给出了相邻块体间接触面抗滑模型的基本原理与适用条件,同时分别从数值模型与实际工程角度验证说明了该抗滑模型在解决相邻块体结构抗滑与分析接触面动力特性上的适用性与优越性。建立的抗滑模型可以更好地模拟实际工程中块体周边接触面上的黏结与抗滑性质,并将单一块体动力问题扩展到相邻块体上,更好地模拟局部块体在强震作用下的动态响应特性。

1相邻块体接触面抗滑模型

1.1块体与周边岩体间接触面抗滑模型

地下洞室块体在滑动过程中受到的抗滑力既包括切向摩擦力,也包括黏聚力[11-12]。结合广义摩尔库伦模型，可将块体与基岩结构间接触面上的切向力描述为以下形式[13-14]:

(1)

式中:τct——块体与岩体接触面上切向应力,Pa;τcn——块体与岩体接触面上法向应力,Pa;kt——接触面切向刚度,Pa/m;ut——接触面上切向相对变形,m;f——接触面上的摩擦系数;c——块体与岩体结构接触面上的黏聚力,Pa;sgn( )——符号函数,给定接触面抗滑力的符号与方向。

1.2相邻块体间接触面抗滑模型

地下洞室相邻块体的特点是块体间有一个或多个面处于接触状态,块体在外力作用下除了与岩体结构有接触作用外,块体间的接触面上也有相对变形和接触作用。在相邻双块体模型中,假定相邻双块体间接触面为平面,按照含有临空面块体的数量,分为2种情况：当相邻块体间的非接触面中每个块体均存在地下洞室的洞室开挖面,此类型相邻块体在本文中简称“Ⅰ类相邻块体”, 模型简化的典型情况见图1;当相邻块体间的非接触面中有且只有一个块体存在地下洞室的洞室开挖面,在本文中简称“Ⅱ类相邻块体”,模型简化的典型情况见图2。

图1　Ⅰ类相邻块体示意图Fig. 1　Adjacent blocks of type Ⅰ

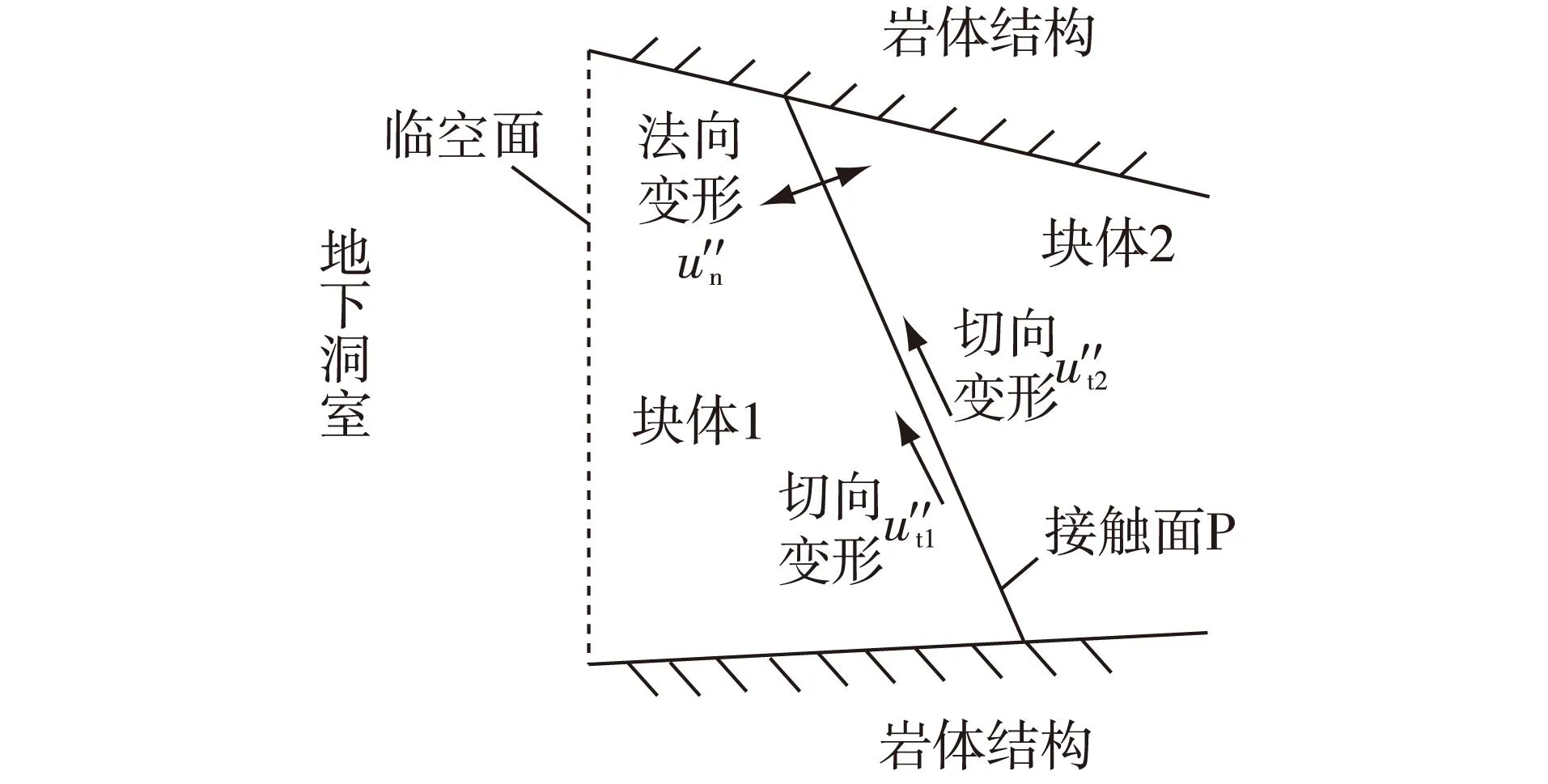
图2　Ⅱ类相邻块体示意图Fig. 2　Adjacent blocks of type Ⅱ

1.2.1Ⅰ类相邻块体

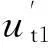
(2)

1.2.2Ⅱ类相邻块体

图2中,同样假设2个块体间的接触面为P,块体1简称为“内侧块体”,其在P上的变形为u″t1,块体2简称为“外侧块体”,其在P上的变形为u″t2,接触界面间的切向相对变形为Δu″t,法向变形为u″n,切向应力为τ″ct,切向刚度为k″t,黏聚力为c″,相应块体间接触面上的抗滑模型动力特性可以按以下公式进行描述:

(3)

2数值模型分析

2.1模型建立

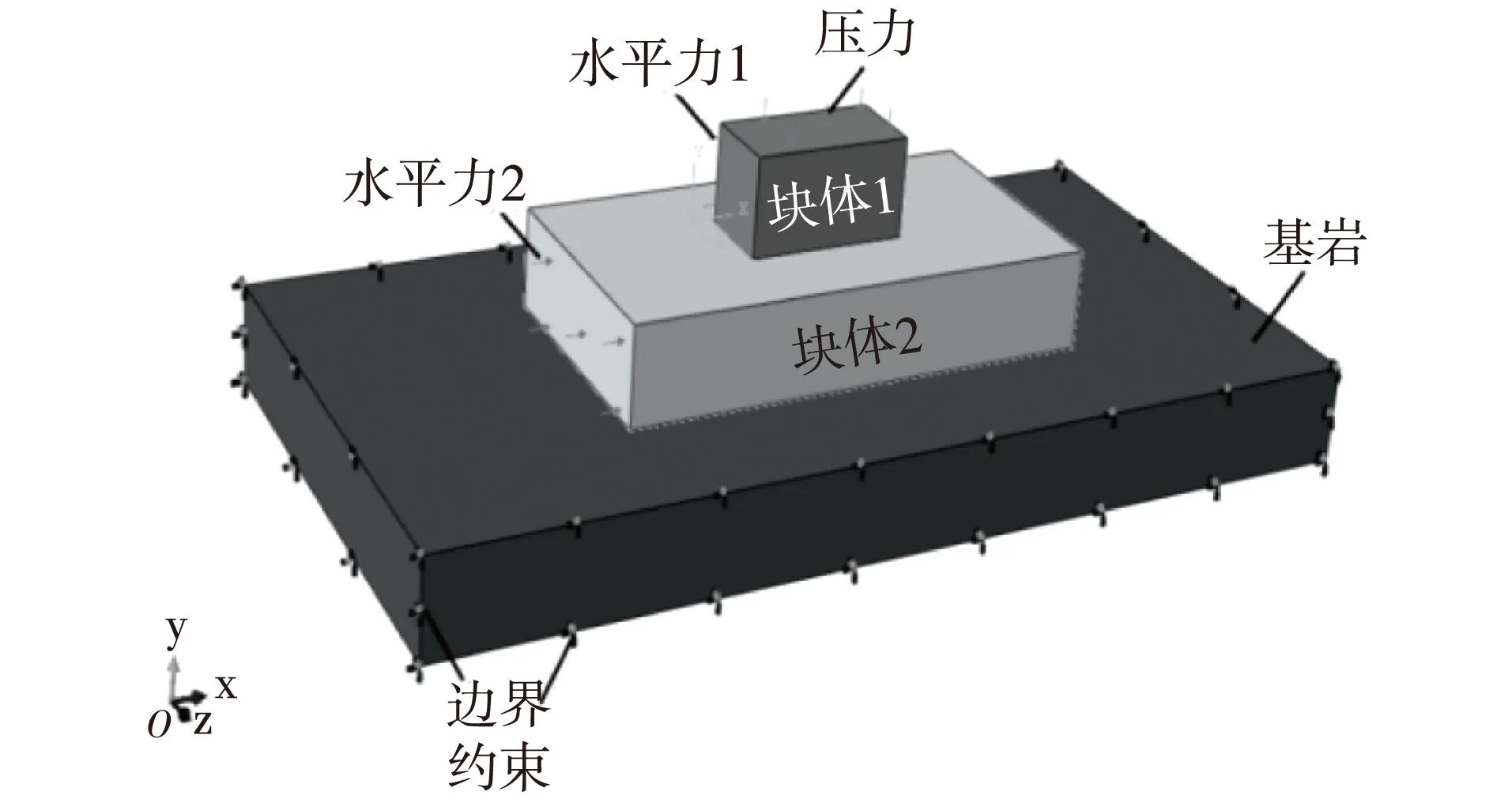
图3　数值模型Fig. 3　Numerical model

为研究理论模型的适用性,建立了图3所示的数值模型。其中块体1尺寸为20 m×10 m×10 m(长×宽×高),块体2尺寸为60 m×30 m×10 m,下部基岩结构尺寸为120 m×60 m×10 m。各结构赋予相同材料属性,密度为2 500 kg/m3,弹性模量为30 GPa,泊松比为0.20,对下部基岩结构底面采用全约束,侧面采用法向约束。在加载时首先对块体1表面施加一个竖直方向且大小为250 kPa的压力,平衡后再在水平X向对2个块体侧面施加一个时长为8 s的动态推力,且推力最大值为200 kPa,水平荷载归一化时程线如图4所示。

图4　水平荷载归一化时程线Fig. 4　Normalized time-history curve of horizontal loads

2.2模型结果分析

图5给出2种抗滑模型条件下,上、下块体的加速度响应情况。从图5中可以看出,采用经典抗滑模型(经典库伦模型)与修正抗滑模型时,下部块体滑动分别出现在总加载时间的第2.7 s和2.9 s时,上部块体的最终稳定加速度分别为2.0 m/s2和1.33 m/s2，下部块体的最终稳定加速度分别为1.80 m/s2和1.25 m/s2,后者动态响应均小于前者计算结果,说明修正抗滑模型对于块体结构运动状态影响的合理性。

图6给出了2种抗滑模型条件下2块块体间及下部块体与基岩间接触面上剪应力曲线。上部块体相对于下部块体滑动后的最终恒定剪应力分别为40.0 kPa和44.6 kPa。下部块体与岩体间接触面上,块体滑动后出现的最大剪应力分别为25.9 kPa和30.6 kPa,结果体现了修正模型中黏聚力的重要作用。

3工 程 实 例

3.1工程概况与模型建立

工程实例位于澜沧江下游,采用NURBS-TIN-BRep混合数据结构与几何建模技术建立工程中的复杂地形体与地下结构,并基于块体理论耦合随机结构面网络模拟技术快速建立地下洞室区域内的曲面块体[6]。选取2类相邻块体为研究对象,建立的地形、洞室及块体模型分别见图7和图8,模型尺寸为837 m×446 m×(299～551)m(长×宽×高)。地下洞室岩体以Drucker-Prager强度准则作为屈服准则,岩体的弹性模量为16 GPa,密度为2.71 g/cm3,泊松比为0.23,抗拉强度为1.6 MPa,内摩擦角为52°,采用瑞利阻尼模拟。地震激励采用唐山余震天津医院地震波,输入方向为水平X向,地震波峰值加速度为1.46 m/s2,加载时间为19.20 s,根据文献[15]对地表地震波进行处理后,获得基岩处的地震波加速度时程曲线。

图5　块体滑动加速度曲线Fig. 5　Curves of sliding acceleration of blocks

图6　接触面剪应力曲线Fig. 6　Curves of shear stress on contact surface

图7　Ⅰ类相邻块体与地基位置的注释图Fig. 7　Position of foundation and adjacent blocks of type Ⅰ

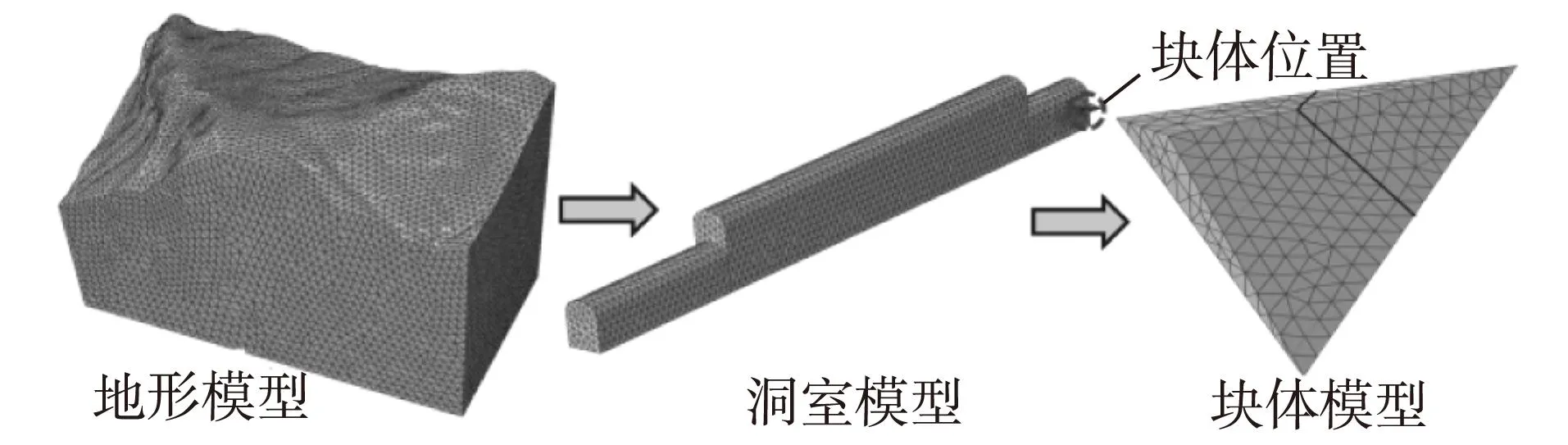
图8　Ⅱ类相邻块体与地基位置的注释图Fig. 8　Position of foundation and adjacent blocks of type Ⅱ

3.2Ⅰ类相邻块体响应分析

图9给出2种抗滑模型条件下相邻两块体水平X向相对位移对比。采用经典模型与修正模型时左侧与右侧块体水平X向最大位移分别为5.42 cm和4.87 cm与5.06 cm和4.77 cm,地震阶段的均方根值分别为2.16 cm和2.02 cm与2.00 cm和1.94 cm。修正模型条件下的位移在数值上相对小于经典模型计算结果,说明在考虑块体黏结效应的抗滑模型在Ⅰ类相邻两块体应用中具有较好适用性。

图9　Ⅰ类相邻块体水平X向相对位移Fig. 9　Relative displacement of adjacent blocks of type Ⅰ in horizontal X direction

图10给出了在2种模型条件下两块体与基岩接触面上代表点的剪切应力对比。基于修正抗滑模型计算获得的剪切应力在数值上大于经典模型结果,修正模型条件下两块体最大剪切应力值分别为0.80 MPa与0.58 MPa,经典模型为0.60 MPa与0.56 MPa,平均剪切应力分别为0.68 MPa与0.44 MPa和0.52 MPa与0.35 MPa,说明块体与基岩间的黏聚力对结构动态特性起到的作用。

图10　Ⅰ类相邻块体剪切应力Fig. 10　Shear stress of adjacent blocks of type Ⅰ

3.3Ⅱ类相邻块体响应分析

图11给出了2种抗滑模型条件下两块体运动的水平X向相对位移。可以看出,修正模型条件下的位移在数值上相对小于经典模型计算结果,外侧块体与内侧块体在整个地震阶段经典与修正模型最大水平X向位移分别为8.42 cm和8.24 cm与8.34 cm和8.13 cm,整个地震阶段水平位移均方根值分别为3.68 cm和3.65 cm与3.55 cm和3.54 cm。以上计算结果说明在地震荷载作用下,发生滑动的块体在修正模型的影响下发生的运动程度要小于在经典模型下的激励效果。

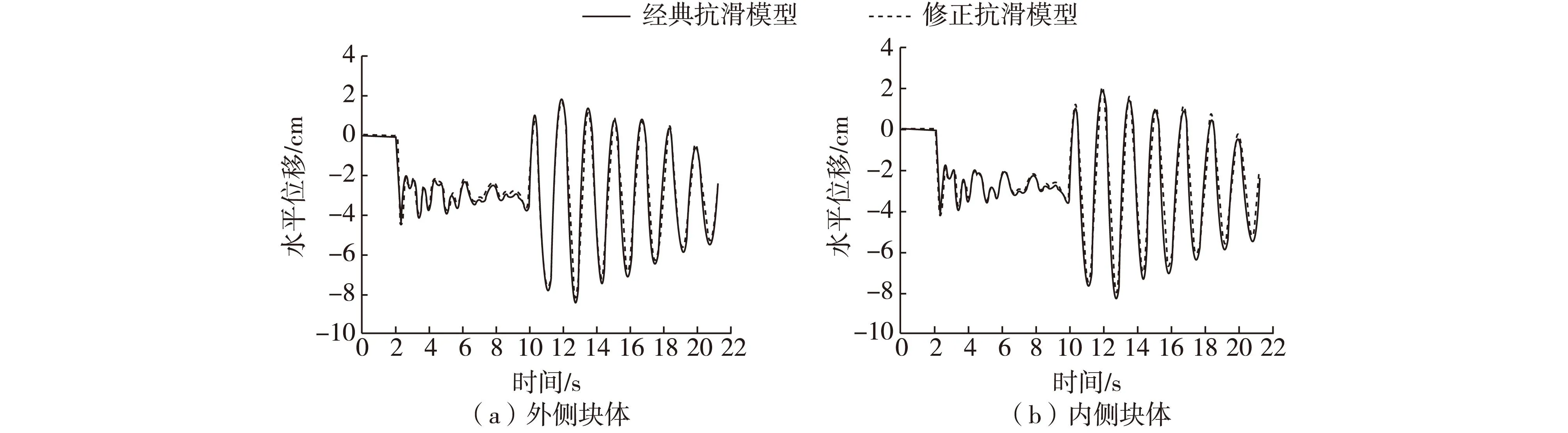
图11　Ⅱ类相邻块体水平X向相对位移Fig. 11　Relative displacement of adjacent blocks of type Ⅱ in horizontal X direction

图12给出了2种抗滑模型条件下两块体与基岩接触面上代表点的剪切应力对比。由图12可知,基于修正模型计算结果在数值上要大于经典模型结果,外侧与内侧块体在修正模型条件下最大剪切应力值分别为0.63 MPa与0.094 MPa,经典模型为0.49 MPa与0.099 MPa,平均剪切应力为0.44 MPa与0.072 MPa和0.36 MPa与0.043 MPa,进一步说明块体与基岩间的黏聚力对结构动态特性起到的作用。

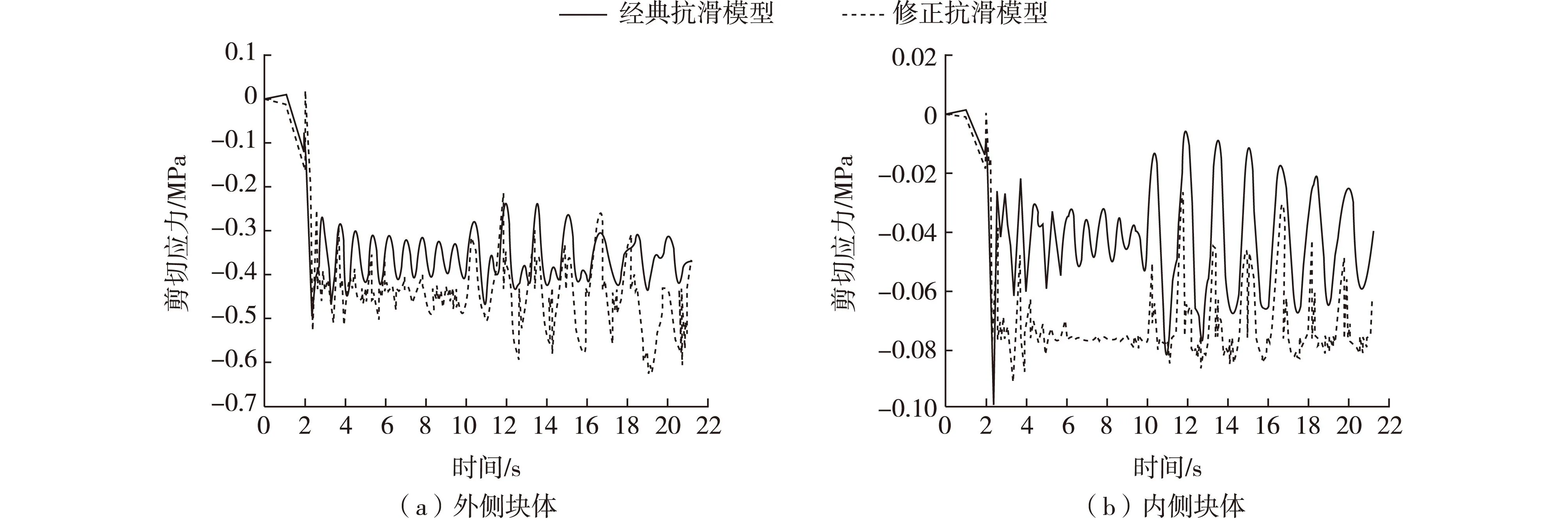
图12　Ⅱ类相邻块体剪切应力Fig. 12　Shear stress of adjacent blocks of type Ⅱ

4结语

本文提出的抗滑模型考虑块体间的相互影响与作用机理,将单一块体稳定性问题扩展到相邻块体上,能够更好地模拟实际工程中块体周边接触面上的摩擦与黏结性质,真实地反映局部块体在强震作用下的动态响应特性。基于数值模型响应结果,修正抗滑模型水平X向相对位移计算结果相对小于经典抗滑模型计算的动力响应,说明地下洞室相邻块体周边接触面动力抗滑模型的可实现性与适用性。针对工程实例,全面分析了相邻块体结构在经典抗滑模型与修正抗滑模型条件下的地震响应与动态特性。研究表明，本文建立的抗滑模型能够更好地模拟实际工程中块体周边接触面上的抗滑与黏结性质,具有较好的工程应用价值。

参考文献：

[1] GOODMAN R E, SHI G H. Block theory and its application to rock engineering[M]. Englewood Cliffs:Prentice-Hall,1985.

[2] GOODMAN R E,TAYLOR R L,BREKKE T L. A model for the mechanics of jointed rock[J]. Journal of Soil Mechanics & Foundations Div,1968,94:637-660.

[3] 石根华.岩体稳定分析的几何方法[J].中国科学,1981(4):487-495.(SHI Genhua. Geometric method of stability analysis of rockmass[J].Science China,1981(4):487-495.(in Chinese))

[4] 郑银河,夏露,于青春.考虑岩桥破坏的块体稳定性分析方法[J].岩土力学,2013,34(增刊1):197-203.(ZHENG Yinhe, XIA Lu, YU Qingchun. Stability analysis method of block considering cracking of rock bridge[J].Rock and Soil Mechanics,2013,34(Sup1):197-203.(in Chinese))

[5] BEYABANAKI S A R,MIKOLA R G,HATAMI K. Three-dimensional discontinuous deformation analysis (3-D DDA)using a new contact resolution algorithm [J].Computers and Geotechnics,2008,35(3):346-356.

[6] OLIVEIRA D A F,INDRARATNA B. Comparison between models of rock discontinuity strength and deformation[J]. Journal of Geotechnical and Geoenvironmental Engineering,2010,136(6):864-874.

[7] ZHONG Denghua, LI Mingchao, LIU Jie. 3D integrated modeling approach togeo-engineering objects of hydraulic and hydroelectric projects[J].Science in China Series E (Technological Science),2007,50(3):329-342.

[8] 钟登华,鲁文妍,刘杰,等. 基于三维地质模型的地下洞室曲面块体分析[J]. 岩石力学与工程学报,2011,30(增刊2):3696-3702.(ZHONG Denghua, LU Wenyan, LIU Jie, et al. Surface-block analysis of underground cavern based on 3D geological modeling[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(Sup2):3696-3702.(in Chinese))

[9] KAIDI S, ROUAINIA M, OUAHSINE A. Stability of breakwaters under hydrodynamic loading using a coupled DDA-FEM approach[J]. Ocean Engineering,2012,55(15):62-70.

[10] 钟登华,鲁文妍,刘杰,等. 复杂地质条件下地下洞室曲面块体地震响应分析[J]. 天津大学学报(自然科学与工程技术版),2014,47(6):471-478.(ZHONG Denghua, LU Wenyan, LIU Jie,et al. Surface-block identification and seismic response analysis of underground structures under complicated geological conditions[J].Journal of Tianjin University(Science and Technology), 2014,47(6):471-478.(in Chinese))

[11] 马永政,郑宏,朱合华,等. DDA 法计算边坡安全系数的黏聚力影响分析[J]. 岩土工程学报,2009,31(7):1088-1093.(MA Yongzheng, ZHENG Hong, ZHU Hehua, et al. Effect of cohesion on evaluating slope stability factor of safety by DDA method[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7):1088-1093.(in Chinese))

[12] 付晓东,盛谦,张勇慧. 基于矢量和一非连续变形分析的滑坡安全系数计算方法研究[J]. 岩石力学与工程学报,2014,33(增刊2):4122-4128.(FU Xiaodong, SHENG Qian, ZHANG Yonghui. Research on safety factor computation of landslide based on vector sum-discontinuous deformation analysis method[J]. Chinese Journal of Rock Mechanics and Engineering,2014, 33(Sup2):4122-4128.(in Chinese))

[13] SU Huaizhi, HU Jiang, LI Jinyou, et al. Deep stability evaluation of high-gravity dam under combining action of powerhouse and dam[J]. International Journal of Geomechanics,2013,13:257-272.

[14] JIANG Yusong, SU Chao. Mixed finite element method for contact problems of multibody[J]. Earth and Space,2010: 606-620.

[15] 鲁文妍.强震作用下大型地下厂房洞室群灾变仿真研究[D].天津:天津大学,2012.

Seismic responses of adjacent blocks in large-scale underground cavern group

LI Wenqian1, TONG Dawei1, WANG Zhen1, ZHU Xiaobin1, LU Wenyan1,2

(1.StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China;2.MaterialsandStructuralEngineeringDepartment,NanjingHydraulicResearchInstitute,Nanjing210029,China)

Abstract:In order to simulate the movement and dynamic response of adjacent blocks in an underground cavern group under seismic loads, a dynamic anti-sliding model, considering the bond strength between the blocks, was established. The effectiveness of the anti-sliding model in comparison to other models was analyzed using a numerical model. In the practical engineering examples, the calculated root mean square values of horizontal displacement in the X direction of two adjacent blocks of type I were 2.16 cm and 2.02 cm when the classical anti-sliding model was used, and 2.00 cm and 1.94 cm when the modified anti-sliding model was used throughout the earthquake process. The corresponding simulated results of two adjacent blocks of type II were 3.68 cm and 3.65 cm when the classical model was used and 3.55 cm and 3.54 cm when the modified model was used. Hence, it is demonstrated that adjacent blocks considering bonding characteristics show much better stability, and the proposed model has high application value.

Key words:underground cavern; adjacent blocks; bonding characteristics; anti-sliding model; seismic responses

DOI：10.3876/j.issn.1000-1980.2016.03.002

收稿日期：2015-10-02

基金项目：国家自然科学基金创新研究群体科学基金(51321065)；国家重点基础研究发展计划(973计划)(2013CB035904)；天津市自然科学基金青年项目(13JCQNJC08900)

作者简介：李文倩(1986—)，女，天津人，博士研究生，主要从事地下洞室模拟与评价分析研究。E-mail：bxqe@163.com 通信作者： 佟大威，讲师。E-mail：tongdw@tju.edu.cn

中图分类号：TV312

文献标志码：A

文章编号：1000-1980(2016)03-0196-07