求解拱坝极限荷载的增量弹性有限元迭代法

钱向东,钮如嵩

(河海大学力学与材料学院,江苏,南京　210098)

求解拱坝极限荷载的增量弹性有限元迭代法

钱向东,钮如嵩

(河海大学力学与材料学院,江苏,南京210098)

摘要：为了克服弹性补偿法每一步计算量太大的问题,结合弹塑性分析法和塑性极限分析法的优点,提出求解复杂结构极限荷载的增量弹性有限元迭代法(IEFEIM)。该方法以荷载因子β为变量,采用自适应增量调整技术,迭代逼近满足平衡条件和屈服条件的最大荷载因子βmax。与弹塑性分析法相比,IEFEIM只需材料的强度准则,不需要材料屈服、破坏后的本构关系;与塑性极限分析法相比,IEFEIM只需增量定向搜索逼近荷载因子最大值,无需开展大范围搜索的规划算法;与弹性补偿法相比,只需形成一次整体刚度矩阵,无需每一步重新形成整体刚度矩阵,可以有效地减少每次迭代的计算量。工程实例表明,IEFEIM可以有效地求得高拱坝的极限荷载,并可以给出临近极限状态时的结构性状。

关键词：拱坝;极限荷载;增量弹性有限元迭代法;拉西瓦水电站

极限荷载是结构承载能力的重要指标,可用于复杂工程结构的整体安全度评价。求解结构极限荷载的方法一般有2种[1]:增量弹塑性分析法和塑性极限分析法。

增量弹塑性分析法的本质是追踪加载历史,以增量形式施加荷载,逐步逼近结构的极限状态。此方法可以了解结构的塑性破坏过程,能够获得加载过程中结构的位移、应变、应力等信息,但必须严格知道结构的加载历史和材料的本构关系。

塑性极限分析法是一种简化的方法,假定材料为理想塑性材料,采用上、下限定理直接对结构的极限状态进行分析,将求解极限荷载的问题转化为一个有约束的数学规划问题。此方法不必考虑结构的加载历史,也无需材料的本构关系,对于简单的结构可以非常方便地求得结构的极限荷载。

为了避免复杂的弹塑性计算和大量的数学规划运算,Mackenzie 等[2]提出了一种简单高效的基于弹性迭代的数值方法,即降低模量法(reduced modulus method), 并发展为弹性补偿法(elastic compensation method,ECM)[3]和修正的弹性补偿法(MECM)[4]。ECM 法仅需要若干步弹性有限元迭代便可求得极限载荷,在每一次弹性有限元分析中,通过调整单元的弹性模量引起应力的重新分布,来模拟塑性失效行为。作为一种评价结构极限承载能力的方法,ECM在压力容器设计与安全评定中得到了广泛应用[5-7]。

拱坝作为典型的三维复杂结构,其极限承载能力的估算一直是难题。一方面,由于混凝土及岩石类材料的力学性能、破坏形式、后继本构关系的复杂性,准确地模拟结构的破坏—失效过程显得非常困难[8-11]。另一方面,由于结构的复杂性,采用有限元与数学规划相结合的极限分析方法[12-15],变量数和约束条件数十分庞大,导致了超高维空间中数学规划的“维数障碍”问题,目前还难以克服。宋鹏等[16]尝试采用弹性补偿法分析拱坝的极限荷载下限,通过承载比均匀度与基准承载比调整单元弹性模量的策略求解极限承载力系数,但所设定的基准荷载以及表达的名义应力并不能合理地反映拱坝的安全或失效性能。

尽管弹性补偿法不需要采用弹塑性本构关系,但每次迭代均需要重新形成一次整体刚度矩阵,求解一个新的弹性问题。迭代过程类似于牛顿法,对大规模问题仍然需要大量的计算时间。

为了克服弹性补偿法每一步计算量太大的情况,笔者拟结合增量弹塑性分析法和塑性极限分析法的优点,针对下限分析,构造一种只需要初始弹性刚度矩阵,通过增量定向搜索确定极限荷载因子近似值的迭代算法。

1下限定理及其积分表达式

下限定理可叙述为:与静力容许场对应的外荷载不大于真实的极限荷载,即任意与静力容许场对应的外荷载是极限荷载的一个下限[17]。因此,所有下限的最大值就是极限荷载。

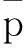
maxβ

(1)

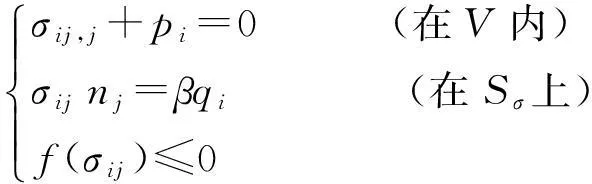
(2)

式中:σij——结构的应力张量;V——结构体;Sσ——结构的应力边界;nj——应力边界的方向余弦;f(σij)≤0——屈服条件。

利用虚功率原理可以将平衡条件和应力边界条件表示为积分形式,则与式(1)(2)等价的下限定理的积分表达式为

maxβ

(3)

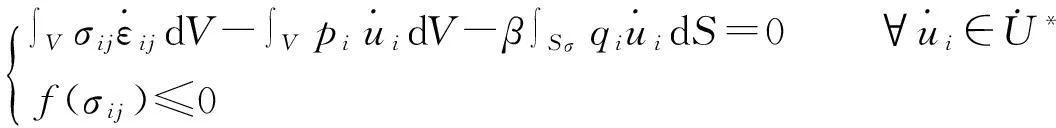
(4)

2下限分析的有限单元法

微分形式(式(1)(2))或积分形式(式(3)(4))所表示的下限定理实质上是一个约束最优化问题。对于复杂结构,难以直接求解,一般可采用有限元法对结构进行离散,建立数值型的约束最优化问题。由积分形式的下限定理可导出下限分析的有限元格式:

maxβ

(5)

(6)

式(5)(6)是一个以β和σ为自变量的约束最优化问题,可以采用线性或非线性规划法进行求解。求解时,为了降低求解空间的维数,常常把寻求与外荷载平衡的应力向量σ转变为寻求自平衡的应力向量σs[1]。

设σp、σq分别为结构在不变荷载Rp、可变荷载Rq作用下的弹性应力,即满足Eσp=Rp、Eσq=Rq，则由E的线性性质可知,弹性应力σE=βσq+σp满足平衡条件:

(7)

假定在荷载βRq+Rp作用下,结构的真实应力由弹性应力σE=βσq+σp和自平衡应力σs叠加而成,即σ=σE+σs,则约束最优化问题(式(5)(6))转换为

maxβ

(8)

(9)

式中:σqi、σpi、σsi——可变荷载弹性应力、不变荷载弹性应力和自平衡应力场对应的第i个Gauss点的应力分量。

式(8)(9)是一个以β和σs为自变量的约束最优化问题,可以采用线性或非线性规划法进行求解。目前已有一系列成熟的线性和非线性规划算法[1,18-21],但是大多数求解非线性规划问题的方法需要处理Hessian矩阵,且对某些屈服函数还存在奇异性。另外,对于复杂的三维结构由于离散系统未知量和约束条件数巨大,求解超高维空间中的数学规划问题存在所谓的“维数障碍”,且解的唯一性和收敛性也有待进一步探讨。

3增量弹性迭代法

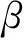
a. 对任意的β>0,有σE=βσq+σp,如果存在一个自平衡应力向量σs, 即Eσs=0,且满足fi(βσqi+σpi+σsi)≤0(i=1,2,…,NF),则βσq+σp+σs是一个静力许可应力场,β是极限荷载因子的一个下限,且β≤βmax。

增量弹性迭代法实施步骤如下:

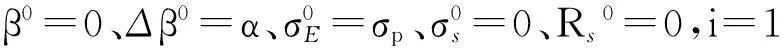
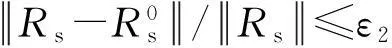
计算中根据应力转移迭代的收敛情况,采用自适应的步长(增量)调整技术,当步长Δβ<εβ时,表明已接近极限状态,即近似达到了βmax。由于与βmax对应的应力场满足全部约束条件,因此βmax是极限荷载因子的一个下限。计算时一般可取α=0.6～1.0,εβ=0.05～0.5,ε1=10-4～10-6和ε2=10-2～10-4。

4工 程 实 例

以黄河拉西瓦水电站的混凝土拱坝为例进行计算分析。该拱坝为高250 m、底宽49 m的对数螺旋式双曲拱坝。计算采用的有限元模型如图1所示,其中模拟了Hf4、Hf6、Hf7、Hf8、Hf10、F166、F164、F29、F172、F211、F201、F421、L145等主要断层和软弱带。

图1　拉西瓦拱坝三维有限元模型Fig. 1　　　　Three-dimensional finite element model for 　　　Laxiwa Arch Dam

计算采用的荷载组合为地应力+坝体自重+水压力(上游正常蓄水位2 542m)+泥沙压力(2 296 m)+渗流+温升。坝体混凝土密度为2.4 t/m3、弹性模量为20 000 MPa、泊松比为0.2、热胀系数为0.000 01 ℃-1。 其他诸如水库运行参数、温度变化情况、岩体结构分布和材料参数等参见文献[22]。

计算时针对不同的材料分别采用不同形式的强度准则。对坝体混凝土采用H-T-C四参数准则[23],岩石采用Drucker-Prager准则,建基面和断层采用修正的Mohr-Coulomb准则。相关强度参数见文献[22]。

根据拱坝的承载特点,以上游水压力作为可按比例增长(超载)的可变荷载,相应的有限元等效结点力为βRq,这里将水压力超载系数作为荷载因子β;地应力、自重、温度、渗流、泥沙等荷载均作为固定荷载,相应的有限元等效结点力为Rp。

采用增量弹性有限元分析时,取α=1.0,即Δβ=1.0、εβ=0.5、ε1=10-5、ε2=10-3。计算过程中当β=7.0时迭代不能收敛,于是开始自动缩减增量步长Δβ,直至Δβ=0.25,即β=6.25时迭代收敛,由于此时Δβ=0.25小于εβ=0.5,加载结束,可获得水压力极限超载系数βmax≈6.25。此计算结果与文献[24]由数值分析和模型试验得出的结果相当吻合,即水荷载超载系数为6.0～8.0。

为了检验临近极限状态时坝体的破坏情况,图2给出了β=6.0和β=6.25时拱坝上下游面的破坏情况。

图2　不同β时上下游面破坏区Fig. 2　Damaged areas on upstream and downstream faces of dam for different values of β

5结语

a. 有限元下限极限分析法可以归结为一个约束最优化问题,荷载因子β既是自变量又是目标函数,可以利用问题的特殊性,寻求有效的求解方法,以克服大规模问题“维数障碍”。

b. 提出的增量弹性有限元迭代法(IEFEIM),结合了增量弹塑性有限元和塑性极限分析两类方法的优点,只需材料的强度准则,不需要材料屈服、破坏后的本构关系;只需增量定向搜索逼近荷载因子最大值,无需开展大范围搜索的规划算法。

c. 与弹性补偿法(ECM)相比,IEFEIM只需形成一次整体刚度矩阵,无需每一步重新形成整体刚度矩阵,可以有效地减少每次迭代的计算量。

d. IEFEIM的本质是常刚度迭代应力转移法,类似于增量弹塑性分析中的常刚度迭代法。转移应力的累加构成一个自平衡应力场。该方法具有简单、高效、易于程序实现等优点。

e. 工程实例的计算表明,该方法可以有效地求得高拱坝的极限荷载,可以给出临近极限状态时的结构性状。

参考文献：

[1] 陈钢,刘应华.结构塑性极限与安定分析理论及工程方法[M].北京:科学出版社,2006.

[2] MACKENZIE D, BOYLE J T. A method of estimating limit loads by iterative elastic analysis I: simple examples [J]. International Journal of Pressure Vessels & Piping, 1992, 53(1):77-95.

[3] MACKENZIE D,SHI J,BOYLE J T.Finite element modeling for limit analysis by elastic compensation method [J].Computer & Structure,1994,51(4):403-410.

[4] 杨璞,刘应华,袁鸿雁,等.计算结构极限载荷的修正弹性补偿法[J].工程力学,2006,23 (3): 21-26.(YANG Pu, LIU Yinghua, YUAN Hongyan, et al. A modified elastic compensation method for the computation of limit loads[J]. Engineering Mechanics,2006,23 (3): 21-26.(in Chinese))

[5] PONTER A R S,CARTER K F.Limit state solutions based on linear elastic solutions with spatially varying elastic modulus[J].Computer Methods in Applied Mechanics and Engineering,1997,140(3/4):237-258.

[6] YANG P,LIU Y,OHTAKE Y,et al.Limit analysis based on a modified elastic compensation method for nozzle-to-cylinder junctions[J].International Journal of Pressure Vessels and Piping,2005,82(10):770-776.

[7] SIMHA C H M, ADIBI-ASL R. Lower bound limit load estimation using a linear elastic analysis[J].Journal of Pressure Vessel Technology,2012, 134(2):1207-1216.

[8] 洪晓林.拱坝坝体非线性分析与极限承载力的估算[D].南京:华东水利学院,1982.

[9] 钱向东.有限单元法在拱坝设计计算中的应用[D].南京:河海大学,1990.

[10] 傅作新,钱向东,郑雄.拱坝极限承载能力的分析方法研究[J].河海大学学报(自然科学版),1991,19(5):25-31.(FU Zuoxin, QIAN Xiangdong, ZHENG Xong. Analysis method of ultimate bearing capacity for arch dam[J]. Journal of Hohai University(Natural Sciences), 1991,19(5):25-31.(in Chinese))

[11] 杨强,程勇刚,赵亚楠, 等.混凝土拱坝的极限分析[J].水利学报,2003，34(10):38-43.(YANG Qiang, CHENG Yonggang, ZHAO Yanan, et al. Limit analysis of concrete arch dam[J]. Journal of Hydraulic Engineering, 2003,34(10):38-43.(in Chinese))

[12] 李新民,王开治.拱坝极限承载力的一个计算方法[J].水利学报,1985，16(7):66-72. (LI Xinmin, WANG Kaizhi. A method for evaluating ultimate bearing capacity of arch dam[J]. Journal of Hydraulic Engineering, 1985，16(7):66-72. (in Chinese))

[13] 杨强,陈新,周维垣,等.推求拱坝极限承载力的一种有效算法[J].水利学报,2002,33(11):60-65.(YANG Qiang, CHEN Xin, ZHOU Weiyuan, et al. An effective method for evaluati, ultimate bearing capacity of arch dam[J]. Journal of Hydraulic Engineering,2002,33(11):60-65.(in Chinese))

[14] 杨强, 程勇刚, 赵亚楠,等.基于非线性规划的极限分析方法及其应用[J].工程力学,2004,21(2):15-19.(YANG Qiang, CHENG Yonggang, ZHAO Yanan, et al. Limit analysis method based on nonlinear programming and its application [J].Engineering Mechanics, 2004,21(2):15-19. (in Chinese))

[15] 王均星,张优秀,王汉辉.高拱坝承载能力研究[J].武汉大学学报(工学版),2004,37(1):27-32.(WANG Junxing, ZHANG Youxiu, WANG Hanhui. Research on load bearing capacity of high arch dam[J]. Engineering Journal of Wuhan University, 2004,37(1):27-32.(in Chinese))

[16] 宋鹏,郑东健,许焱鑫,等.基于弹性补偿法的拱坝极限承载力分析方法[J].水利水电科技进展,2015,35(6):78-81.(SONG Peng,ZHENG Dongjian,XU Yanxin, et al. Analysis approach for ultimate bearing capacity of arch dams based on elastic compensation method[J]. Advances in Science and Technology of Water Resources, 2015,35(6):78-81.(in Chinese))

[17] 徐秉业,刘信声.结构塑性极限分析[M].北京:中国建筑工业出版社,1985.

[18] SLOAN S W. Lower bound limit analysis using finite elements and linear programming[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1988, 12(1):61-77.

[19] LYAMIN A V, SLOAN S W. Lower bound limit analysis using non-linear programming[J]. International Journal for Numerical Methods in Engineering, 2002, 55:573-611.

[20] KRABBENHOFT K, DAMKIDLE L. A general non-linear optimization algorithm for lower bound limit analysis[J]. International Journal for Numerical Methods in Engineering, 2003, 56:165-184.

[21] 钱向东,吴有奇,林荔珊.下限极限分析的子迭代路径跟踪内点算法[J].河海大学学报(自然科学版),2015,43(3):244-248. (QIAN Xiangdong,WU Youqi,LIN Lishan. Subiterative interior point path-following algorithm for lower bound limit analysis[J].Journal of Hohai University(Natural Scineces), 2015,43(3):244-248.(in Chinese))

[22] 钱向东.黄河拉西瓦拱坝三维有限元分析与安全度评价[R].南京:河海大学,2003.

[23] HSIEH S S, TING E C, CHEN W F. A plastic-fracture model for concrete [J]. International Journal of Solids and Structures, 1982, 18(3):181-197.

[24] 黄岩松,周维垣,杨若琼,等.拉西瓦拱坝稳定性分析和评价[J].岩石力学与工程学报, 2006,25(5): 901-905. (HUANG Yansong, ZHOU Weiyuan, YANG Ruoqiong, et al. Stability analysis and evaluation of Laxiwa Arch Dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(5): 901-905. (in Chinese))

Incremental elastic finite element iterative method for solution of ultimate load of arch dams

QIAN Xiangdong, NIU Rusong

(CollegeofMechanicsandMaterials,HohaiUniversity,Nanjing210098,China)

Abstract:In order to avoid large amounts of computation with the elastic compensation method, the incremental elastic finite element iterative method (IEFEIM) is proposed for solution of the ultimate load of complex structures, based on the advantages of elastic-plastic analysis and plastic limit analysis. With the load factor β as a variable, and by using the self-adaptive increment adjustment technique, the maximum load factor βmaxsatisfying the equilibrium and yield conditions is obtained by iteration and approximation. In contrast to the elastic-plastic analysis method, the IEFEIM only requires the strength criterion of materials and does not require the constitutive relationship of materials after yielding and failure; in contrast to the plastic limit analysis method, the IEFEIM obtains the maximum load factor by directional search and approximation, without using the programming algorithm for large-scale search; and in contrast to the elastic compensation method, the IEFEIM generates the global stiffness matrix for only one time, without any need of generating the global stiffness matrix for each step, effectively decreasing the amount of computation in iterations. Practical application in engineering projects shows that the IEFEIM can obtain the ultimate load of high dams effectively and provide the structural characteristics close to the ultimate state.

Key words:arch dam; ultimate load; incremental elastic finite element iterative method; Laxiwa Arch Dam

DOI：10.3876/j.issn.1000-1980.2016.03.003

收稿日期：2015-08-16

基金项目：国家自然科学基金重点项目(11132003)

作者简介：钱向东(1963—),男,江苏吴江人，教授,博士,主要从事工程力学、水工结构工程研究。E-mail:xdqing@hhu.edu.cn

中图分类号：TV642.4

文献标志码：A

文章编号：1000-1980(2016)03-0203-06