优化高维复杂函数的改进人工蜂群算法
2016-06-30王志刚王明刚
王志刚,王明刚
(南京师范大学泰州学院数学科学与应用学院,江苏 泰州 225300)
优化高维复杂函数的改进人工蜂群算法
王志刚,王明刚
(南京师范大学泰州学院数学科学与应用学院,江苏 泰州 225300)
[摘要]针对人工蜂群算法传统搜索策略在求解高维复杂函数时收敛速度较慢、容易陷入局部最优的缺陷,提出了一种改进的人工蜂群算法(IABC).该算法在引领蜂的搜索策略中借鉴了差分进化算法DE/best/1变异操作模式;在跟随蜂的搜索策略中借鉴了生物界中雁群的飞行特征,同时基于目标函数值进行选择寻优,能较好地平衡局部搜索能力和全局搜索能力.通过对15个基准函数的仿真实验及与其他改进算法进行比较,发现该算法具有较快的收敛速度和较高的求解精度.
[关键词]人工蜂群算法;差分进化算法;雁群飞行;搜索策略
0引言
人工蜂群[1](Artificial Bee Colony,ABC)算法是由Karaboga在2005年提出的一种比较新颖的群体智能优化算法.目前,该算法已在众多领域得到了广泛的应用[2-5],并取得了较好的实验结果.但在ABC算法中,引领蜂和跟随蜂所采用的搜索策略在求解高维复杂函数时存在着过早收敛、容易陷入局部最优、求解精度不高等缺点.针对这些问题,许多专家们提出了不同的搜索策略来改善算法的性能[6-13].例如:文献[6]通过引入Rosenbrock旋转方向的办法对引领蜂的搜索策略进行改进,提高了算法的收敛速度;文献[7]受粒子群算法的启发,在原有搜索策略的基础上融入全局最优解的信息来提高算法的局部搜索能力;文献[8]采用混沌映射和反向学习理论初始化种群,然后引入差分变异和一个平衡选择2种搜索机制的概率以提高算法的全局进化性能;文献[9]在ABC算法的搜索策略中通过引入一个扰动概率参数和自适应尺度因子来对ABC算法进行改进;文献[10]在差分进化思想的启发下,提出了ABC/best算法;文献[11]中引领蜂和跟随蜂在执行搜索策略时按照一定的选择概率从5种不同的搜索策略中选取其中一种策略进行搜索;文献[12]提出了一种具有自适应全局最优引导快速搜索策略的人工蜂群算法;文献[13]受分治策略的启发,提出一种基于分治策略的改进人工蜂群算法.
本文提出一种改进的人工蜂群算法,该算法对ABC算法原有搜索策略做了相应改进:在引领蜂的搜索策略中借鉴差分进化算法中DE/best/1变异操作模式;在跟随蜂的搜索策略中借鉴自然界中雁群的飞行特征,同时利用目标函数值进行选择操作.新的搜索策略能够平衡算法的局部搜索能力和全局搜索能力,加快算法的收敛速度,提高寻优精度.为验证本文算法的性能,在15个典型的benchmark函数上进行了仿真实验,并与ABC算法和5种不同类型的改进算法进行了对比.实验结果表明,新算法不仅具有较强的全局搜索能力,而且具有较强的局部搜索能力,在收敛速度和解的精度上均有较大优势.
1人工蜂群算法
在ABC算法中,人工蜂群包含引领蜂、跟随蜂和侦察蜂3种.ABC算法在求解优化问题时,食物源代表优化问题的一个可能解,蜂群采蜜(食物源)的过程也就是搜寻优化问题最优解的过程.食物源的优劣取决于优化问题的适应值,适应值高的食物源较优.ABC算法中解的个数(SN)等于引领蜂或跟随蜂的个数.用xi=(xi1,xi2,…,xiD)表示第i个食物源(i=1,2,…,SN,D为搜索空间的维数).人工蜂群搜索食物源的过程:(1)引领蜂对当前食物源进行邻域搜索,产生候选食物源,并通过贪婪选择较优的食物源;(2)跟随蜂根据引领蜂分享的信息选择一个食物源,进行邻域搜索产生候选食物源,并通过贪婪选择较优的食物源;(3)引领蜂放弃食物源,变为侦察蜂,并随机搜索新的食物源.
引领蜂和跟随蜂根据
vij=xij+φij(xij-xkj)
(1)
在食物源的邻域生成一个候选食物源.式中:vij是生成的候选食物源,k∈{1,2,…,SN},j∈{1,2,…,D},k和j这2个数都是随机选取的,但k≠i,φij是[-1,1]上均匀分布的随机数.(1)式称为ABC算法的搜索策略.
跟随蜂通过
(2)
概率来选择食物源.式中fiti为第i个食物源的适应值.在最小化问题中,fiti与优化问题目标函数值fi的对应关系为
(3)
在ABC算法中,如果连续经过limit次循环之后食物源仍然没有得到更新,则引领蜂就放弃食物源,转变为侦察蜂,并按
(4)
2改进的人工蜂群算法(IABC)
2.1ABC算法中搜索策略的不足
在ABC算法的搜索策略中主要存在2个问题:(1)搜索策略(1)式中含有j,k和φij3个随机项,这使得算法在搜索过程中有更多的不确定性,虽然具有较好的全局搜索能力,但局部搜索能力不足,导致算法存在着收敛速度慢、求解精度低的问题[7];(2)在ABC算法中,引领蜂负责在特定的范围内搜索食物源,并将搜索到的信息共享给跟随蜂,跟随蜂选择较好的食物源做进一步的搜索,以便找到更好的食物源,而引领蜂和跟随蜂使用相同的搜索策略与算法模拟蜂群采蜜的过程相矛盾[12].
2.2新的搜索策略
针对ABC算法搜索策略存在的不足,我们对ABC算法中引领蜂和跟随蜂的搜索策略做相应改进.
2.2.1引领蜂的搜索策略
为提高算法的局部搜索能力,加快收敛速度,借鉴差分进化算法中DE/best/1的变异操作模式[8],将式(1)变为
vij=xbest,j+φij(xrj-xkj).
(5)
其中:xbest,j为种群的全局最优解;r,k∈{1,2,…,SN},j∈{1,2,…,D},且r≠k≠i.
(5)式在种群的全局最优解附近产生候选食物源,通过种群的全局最优解来引导种群的搜索轨迹,加快算法的收敛速度,以增强算法的局部搜索能力.因此,把(5)式作为新算法中引领蜂的搜索策略.
2.2.2跟随蜂的搜索策略
雁群在飞行时常常呈现“人”字形或“一”字形,其中头雁扇动双翼产生尾涡,后面尾随的大雁借力飞行,雁群中最强壮的大雁往往作为头雁,其他大雁依次往后排[14].借鉴雁群的这种飞行特征,可以把大雁的强壮程度视为食物源的优劣,将食物源按照适应值的优劣进行排序,把最优的食物源作为头雁,剩余的依次往后排,跟随蜂在食物源xi附近按照
vij=xi-1,j+φij(xi-1,j-xkj)
(6)
产生候选食物源.其中xi-1为按照食物源的适应值优劣排在xi前的食物源.(6)式在产生候选食物源时可以充分利用整个种群的信息,避免了所有候选食物源都在种群的全局最优解附近产生,这有利于在搜索过程中找到更优秀的个体,增强了算法跳出局部最优的可能.
2.3基于目标函数值的选择寻优
在ABC算法中,引领蜂、跟随蜂和侦察蜂在对食物源的选择过程中都是基于适应值fiti,如果候选食物源的适应值优于之前食物源,则取而代之.但从(3)式可以看出,对于函数优化问题的目标函数值大于0且无限接近0时,对应的适应值fiti就不具有区分度.为解决这个问题,本文算法在引领蜂、跟随蜂和侦察蜂对食物源的选择过程中直接采用目标函数值来代替适应值[15].
2.4IABC算法的步骤
改进算法的具体步骤如下:
步骤1设置算法的各个参数,初始化种群,计算每个引领蜂对应的食物源的目标函数值并记录全局最优值;
步骤2对每个引领蜂,根据(5)式对食物源进行更新并计算其目标函数值,通过贪婪选择较优的食物源;
步骤3计算更新后食物源的目标函数值,并按(2)式计算选择概率Pi;
步骤4跟随蜂依据概率Pi选择食物源,根据(6)式对食物源进行更新并计算其目标函数值,通过贪婪选择较优的食物源;
步骤5若引领蜂对应的食物源连续limit次没有得到更新,则对应的引领蜂变为侦察蜂,根据(4)式产生新食物源;
步骤6记录下全局最优值,并跳转至步骤2,直至满足算法结束条件.
3仿真实验
为了验证本文提出的IABC算法的性能,选取了15个基准测试函数用于仿真实验,并与ABC算法、文献[7]提出的算法(记为GABC)的测试结果进行比较.实验时,种群规模SN=20,limit=SN×D,最大评价次数MaxFEs=5 000×D.在实验中,3种算法在每个函数上独立运行10次,记录结果的最优值(Best)、最差值(Worst)、平均值(Mean)和标准差(Std).其中:Best和Worst反映了解的质量;Mean反映了算法在给定的最大评价次数下所能达到的精度;Std反映了算法的稳定性和鲁棒性.
表1给出了15个基准测试函数的表达式、搜索范围和理论最优值,其中,f1(x)-f8(x)为单峰函数,f9(x)-f15(x)为多峰函数.表2和3分别给出了ABC、GABC和IABC在D=30和D=100时的测试结果.

表1 基准测试函数

表2 ABC、GABC和IABC在函数维数为30时的测试结果

表3 ABC、GABC和IABC在函数维数为100时的测试结果
从表2可以看出,在单峰函数的测试中,除了f8(x)外,IABC算法在解的精度和稳定性两方面都优于ABC算法和GABC算法.在多峰函数的测试中,对于f9(x)和f10(x),3种算法都能得到理论最优值.对于其他的复杂多峰函数,IABC算法的求解结果明显优于ABC算法和GABC算法.为了直观地反映IABC算法的收敛性能,图1—6给出了3种算法对于部分测试函数在30维数时的收敛曲线.从图1—6中可以看出,IABC算法在迭代初期就有良好的性能,测试函数的收敛曲线下降速度很快,能够收敛到较高精度的解.
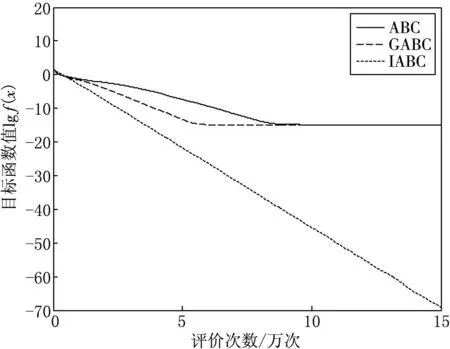
图1 Schwefel 2.22函数收敛曲线

图2 Schwefel 2.21函数收敛曲线

图3 Quartic函数收敛曲线

图4 Griewank函数收敛曲线

图5 Ackley函数收敛曲线
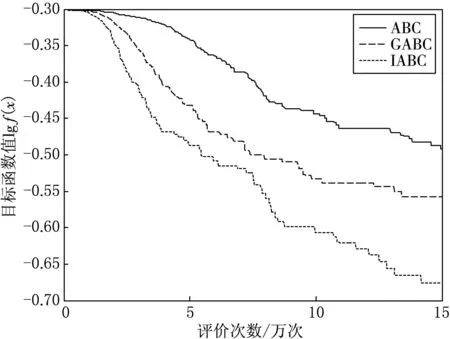
图6 Schaffer函数收敛曲线
从表3可以看出,对于D=100,IABC算法也取得了与D=30时一样好的优化结果,即对于15个测试函数,除f8(x)外,IABC算法的结果都优于ABC算法和GABC算法.
为进一步测试IABC算法的性能,将其与MABC[8]、ABCBest1[10]、ABCBest2[10]、ABCVSS[11]等较新的改进算法在D=30和D=100时进行了比较,所有算法的最大评价次数MaxFEs=5 000×D.表4—5给出了5种算法的测试结果.

表4 5种算法在函数维数为30时的测试结果
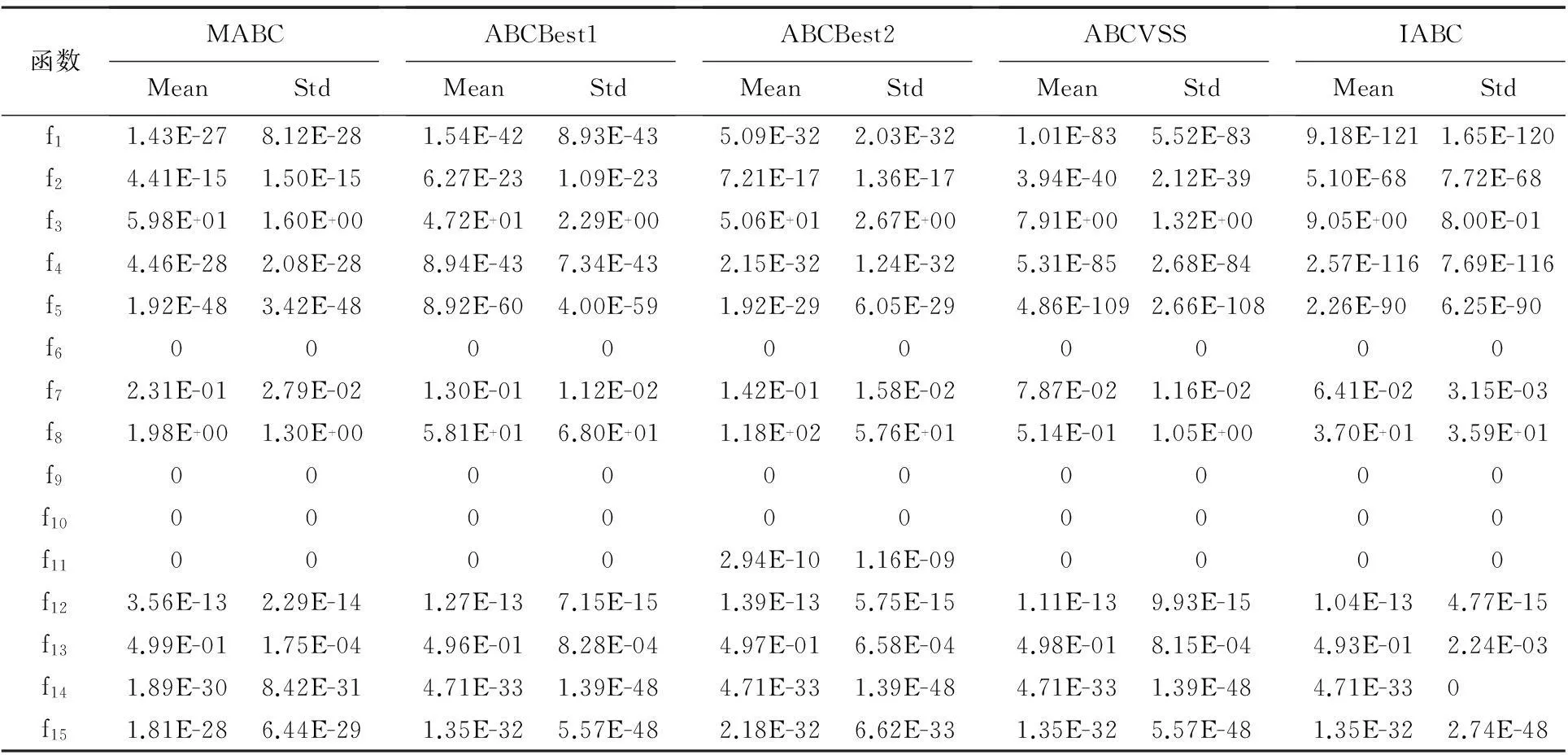
表5 5种算法在函数维数为100时的测试结果
由表4和5可以看出,在15个基准测试函数中,对于f6(x),f9(x)和f10(x),5种算法都能求得理论最优值,对于其他函数,IABC算法在解的精度和稳定性两方面明显优于MABC、ABCBest1、ABCBest2,在绝大部分函数上优于ABCVSS.
从上述实验结果可以看出,IABC算法在计算精度上有了明显提高,不仅具有较强的全局搜索能力,而且具有较强的局部搜索能力,能有效克服ABC算法收敛速度慢和易陷入局部最优的缺陷,并且随着目标函数维数的增加,仍能保持较好的有效性和鲁棒性.
4结论与展望
针对人工蜂群算法传统搜索策略容易导致算法陷入早熟、搜索效率较低的缺点,提出了一种改进的人工蜂群算法,新算法提高了搜索效率.借鉴差分进化算法中的变异操作和生物界中雁群的飞行特征分别对人工蜂群算法中引领蜂和跟随蜂的搜索策略进行改进,并直接基于目标函数值选择寻优.对15个基准测试函数进行仿真实验.结果表明,新算法在优化性能和鲁棒性等方面较基本人工蜂群算法及一些改进的人工蜂群算法有了较大的改善.
当然,新算法也存在着一些不足,对于Rosenbrock函数,IABC算法的求解效果并不是很好.如何使算法能够在更多复杂函数上表现更好的性能将是下一步的研究方向.同时,将所提出的算法应用到约束优化、多目标优化以及非线性系统优化等领域也是值得进一步研究的任务.
[参考文献]
[1]KARABOGA D.An idea based on honey bee swarm for numerical optimization[R].Kayseri:Erciyes University,2005.
[2]KARABOGA N.A new design method based on artificial bee colony algorithm for digital IIR filters[J].Journal of the Franklin Institute,2009,346(4):328-348.
[3]SINGH A.An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem[J].Applied Soft Computing,2009,9(2):625-631.
[4]TASGETIREN M F,PAN Q K,SUGANTHAN P N,et al.A discrete artificial bee colony algorithm for the total flowtime minimization in permutation flow shops [J].Information Sciences,2011,181(16):3459-3475.
[5]SZETO W,WU Y,HO S C.An artificial bee colony algorithms for the capacitated vehicle routing problem[J].European Journal of Operational Research,2011,215(1):126-135.
[6]KANG F,LI J L,MA Z Y.Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions[J].Information Sciences,2011,181(16):3508-3531.
[7]ZHU G P,KWONG S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173.
[8]GAO W F,LIU S Y.A modified artificial bee colony algorithm[J].Computer & Operations Research,2012,39(3):687-697.
[9]AKAY B,KARABOGA D.A modified artificial bee colony algorithm for real-parameter optimization[J].Information Sciences,2012,192(1):120-142.
[10]GAO W F,LIU S Y,HUANG L L.A global best artificial bee colony algorithm for global optimization[J].Journal of Computational and Applied Mathematics,2012,236(11):2741-2753.
[11]KIRAN M S,HAKLI H,GUNDUZ M,et al.Artificial bee colony algorithm with variable search strategy for continuous optimization[J].Information Sciences,2015,300(8):140-157.
[12]赵辉,李牧东,翁兴伟.具有自适应全局最优引导快速搜索策略的人工蜂群算法[J].控制与决策,2014,29(11):2041-2047.
[13]李田来,刘方爱,王新华.基于分治策略的改进人工蜂群算法[J].控制与决策,2015,30(2):316-320.
[14]刘金洋,郭茂祖,邓超.基于雁群启示的粒子群优化算法[J].计算机科学,2006,33(11):166-168.
[15]BANHARNSAKUN A,ACHALAKUL T,SIRINAOVAKUL B.The best-so-far selection in artificial bee colony algorithm[J].Applied Soft Computing,2011,11(2):2888-2901.
(责任编辑:石绍庆)
Improved artificial bee colony algorithm for solving complex functions with high dimensions
WANG Zhi-gang,WANG Ming-gang
(School of Mathematics and Apply,Nanjing Normal University Taizhou College,Taizhou 225300,China)
Abstract:The traditional search strategy of artificial bee colony algorithm exists some disadvantages when solving complex functions with high dimensions,such as the convergence speed is not fast enough,easy to fall into local optimum.In order to solve these issues,an improved artificial bee colony algorithm is presented.In this algorithm,the search strategy of employed bees uses the DE/best/1 mutation operation of the differential evolution for reference,the search strategy of onlookers uses the characteristics of the flight of geese for reference,and select the best solution based on the objective function value.The new algorithm can balance the ability of local and global search.Experiments are conducted on a set of 15 benchmark functions,and the results demonstrate that the new algorithm has fast convergence and high accuracy than several other ABC-based algorithms.
Keywords:artificial bee colony algorithm;differential evolution;flight of geese;search strategy
[文章编号]1000-1832(2016)02-0056-09
[收稿日期]2015-09-06
[基金项目]国家自然科学基金资助项目(71503132);江苏省高校自然科学研究项目(14KJD110005,14KJB110017);南京师范大学泰州学院数学建模精品课程项目.
[作者简介]王志刚(1978—),男,讲师,主要从事组合优化与智能优化算法研究;王明刚(1982—),男,副教授,主要从事智能优化算法、复杂系统建模与控制研究.
[中图分类号]TP 301.6[学科代码]520·30
[文献标志码]A
[DOI]10.16163/j.cnki.22-1123/n.2016.02.014
