黎曼流形上漂移薛定谔算子的加权特征值估计

谭沈阳，黄体仁，张学华

(1.南京理工大学泰州科技学院基础部，江苏 泰州 225300;2.浙江理工大学数学系，浙江 杭州 310018;3.黄山学院数理统计学院，安徽 黄山 245041)

黎曼流形上漂移薛定谔算子的加权特征值估计

谭沈阳1，黄体仁2，张学华3

(1.南京理工大学泰州科技学院基础部，江苏 泰州 225300;2.浙江理工大学数学系，浙江 杭州 310018;3.黄山学院数理统计学院，安徽 黄山 245041)

[摘要]研究了黎曼流形上漂移薛定谔算子-Δφ+V的加权特征值估计问题，利用试验函数方法得到了特征值的杨洪仓型不等式，同时得到了高阶特征值的上界估计，将已有文献结果推广到更一般的情形.

[关键词]黎曼流形；特征值估计；漂移拉普拉斯

0引言

1956年Payne等[1]考虑了下列固定膜问题

(1)

得到了特征值的一个全局不等式，并将之推广到n维情形即PPW不等式

(2)

1980年Hile和Protter[2]得到了下面的HP不等式

1991年杨洪仓[3]证明了著名的第一杨型不等式

和第二杨型不等式

关于算子特征值的研究进展可参考文献[1-5].

近来一些数学家研究了权重黎曼流形上的漂移拉普拉斯算子的特征值问题[6-8]

(3)

其中φ是定义在Ω上的光滑函数.2013年夏昌玉和许洪伟[9]考虑了黎曼流形上该算子的特征值估计，得到了一个杨型不等式

本文主要考虑特征值问题

(4)

其中v表示非负位势函数，ρ为M上正的连续函数.

由分部积分可知

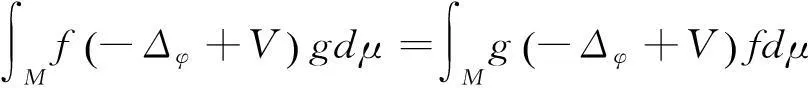
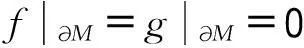
0<λ1≤λ2≤…≤λr≤….

本文通过试验函数的方法得到了关于算子-Δφ+v特征值的一个广义不等式，并通过特殊的试验函数得到了一个杨洪仓型不等式，该结果包含了夏昌玉和许洪伟[9]的结果.

1一个关键引理

引理1假设λi为问题(4)的第i个特征值，μi为λi的正交特征函数，即

(5)

则对任意的h∈C3(M)∩C2(∂M)和任意的整数k，

(6)

证明定义试验函数

(7)

其中

Aij=∫Mρhuiujdμ=Aji.

则

∫Mρφiujdμ=0，φi|∂M=0，∀i，j=1，…，k.

(8)

直接计算可知

(9)

将(9)式代入著名的Rayleigh-Ritz不等式得

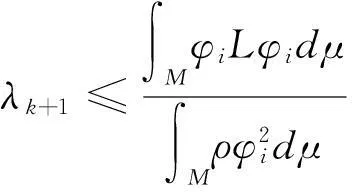
(10)

(11)

令

(12)

则

(13)

令

(14)

利用(8)，(12)，(13)式与hölder不等式得

(15)

从而

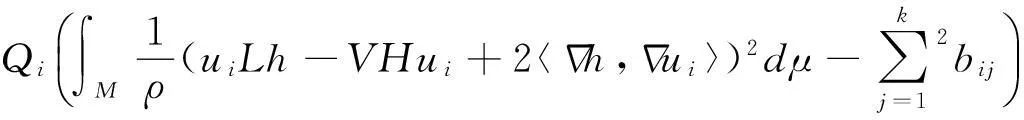
(16)

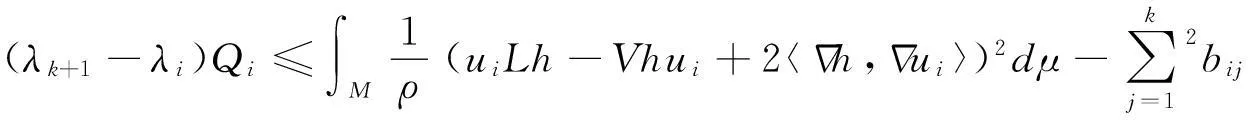
(17)

另一方面，根据(14)式有

(18)

将(18)式代入(17)式中并将i从1加到k得

(19)

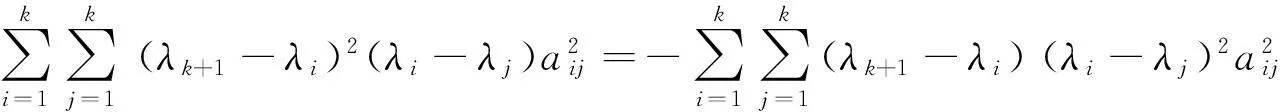
(20)

将(20)式代入(19)式中即可完成证明.

2主要结果及证明

引理2假设M为n维完备黎曼流形，Ω⊂M为具有光滑边界的有界区域，φ为Ω上的光滑函数，λi为下面问题的第i个特征值

(21)

如果M等距嵌入到Rm且平均曲率为h，则

(22)

证明设xα(α=1，2，…，m)为Rm的标准坐标函数，在(22)式中取h=xα，关于α从1加到m有

(23)

(24)

同时

Δ(x1，x2，…，xm)≡Δ(x1，x2，…，xm)=nH，

(25)

(26)

(27)

将(24)─(27)式代入(23)式即可完成引理的证明.

定理1假设引理2的条件均成立，令

则

(28)

证明显然

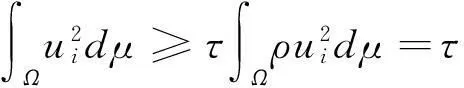
(29)

(30)

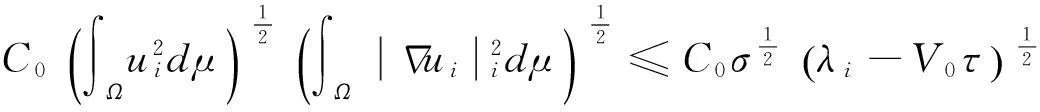
(31)

将(29)─(31)式代入(22)式即可证得定理结论.

注当ρ=1，v=0时定理1的结论即为文献[9]中的结果.

易见不等式(28)是一个二次不等式，通过解该不等式可得关于特征值的第二杨洪仓型不等式.

推论1假设引理2条件成立，则

(32)

其中

注由推论1易知第k+1个特征值可以用前面的k个低阶特征值来控制

[参考文献]

[1]PAYNE L E，POLYA G，WEINBERGER H F.On the ratio of consecutive eigenvalues[J].J Math and Phis，1956，35:289-298.

[2]HILE G N，PROTTER M H.Inequalities for eigenvalues of the Laplacian[J].Indiana Univ Math J，1980，29：523-538.

[3]ASHBAUGH M S.Universal eigenvalue bounds of Payne-Polya-Weinberger[J].Proc Indian Acad Sci，2002，112：3-30.

[4]CHENG Q M，YANG H C.Inequalities for eigenvalues of Laplacian on domains and compact hypersurfaces in complex projective spaces[J].J Math Soc Japan，2006，58：545-561.

[5]EVANS II.Some geometric bounds on eigenvalue gaps[J].Comm in Part Diff Eqns，1993，18：179-198.

[6]MA L，LIU B Y.Convex eigenfunction of a drifting Laplacian operator and the fundamental gap [J].Pacific J Math，2009，240：343-361.

[7]MA L，LIU B Y.Convexity of the first eigenfunction of the drifting Laplacian operator and its applica-tions [J].New York J Math，2008，14:393-401.

[8]MA L，DU S H.Extension of Reilly formula with applications to eigenvalue estimates for drifting Laplacians[J].C R Math Acad Sci Paris，2010，348：1203-1206.

[9]XIA C Y，XU H W.Inequalities for eigenvalues of the drifting Laplacian on Riemannian manifolds[J].Ann Glob Anal Geom，2014，45：155-166.

[10]FRIEDRICHS K O.Spectral theory of operators in Hilbert space[M].New York:Springer Verlag，1980:143-163.

(责任编辑：李亚军)

nequalities for weighted eigenvalues of the drifting Schrodinger operator on Riemannian manifolds

TAN Shen-yang1，HUANG Ti-ren2，ZHANG Xue-hua3

(1.Department of Basic Courses，Taizhou Institute of Science and Technology，Taizhou 225300，China; 2.Department of Mathematics，Zhejiang Science and Technology University，Hangzhou 310018，China; 3.School of Mathematics and Statistics，Huangshan University，Huangshan 245041，China)

Abstract:The Dirichlet weighted eigenvalue problem of the operator -Δφ+V on compact Riemannian manifolds is investigated，where Δφis the drifting Laplacian operator on compact Riemannian manifolds.A yang-type inequality of this problem is established.Estimates for upper bounds of higher order eigenvalues are also obtained.

Keywords:Riemannian manifolds；eigenvalue estimates；drifting Laplacian

[文章编号]1000-1832(2016)02-0035-05

[收稿日期]2014-12-10

[基金项目]国家青年自然科学基金资助项目(11401531)；江苏省高校自然科学基金资助项目(14KJD110004).

[作者简介]谭沈阳(1982—)，硕士，主要从事微分几何研究.

[中图分类号]O 186[学科代码]110·2745

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.009