一类差分方程组的亚纯允许解

金　瑾

(1.贵州工程应用技术学院数学系，贵州 毕节 551700；2.毕节循环经济研究院，贵州 毕节 551700)

一类差分方程组的亚纯允许解

金瑾1，2

(1.贵州工程应用技术学院数学系，贵州 毕节 551700；2.毕节循环经济研究院，贵州 毕节 551700)

[摘要]利用亚纯函数的Nevanlinna值分布理论，研究了一类差分方程组的亚纯解的存在性问题.得到差分方程组的亚纯解或同为允许、或同为非允许的结论，进而得到了更一般的结果.

[关键词]差分方程组；亚纯函数；允许解；Nevanlinna理论；值分布理论

1预备知识

我们假设读者熟悉亚纯函数的Nevanlinna值分布理论的基本知识和通常记号.[1-19]关于微分方程组的允许解问题，有很多作者做了大量的工作，得到了一大批很好的结果.[1-12]

对下面的高阶非线性代数微分方程组

(1.1)

其中

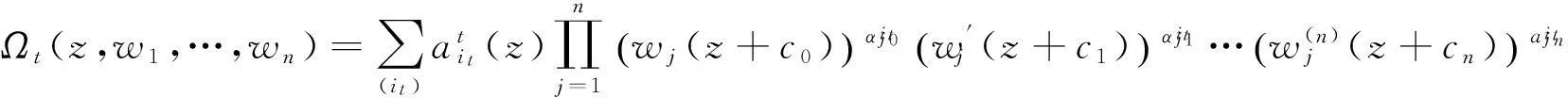
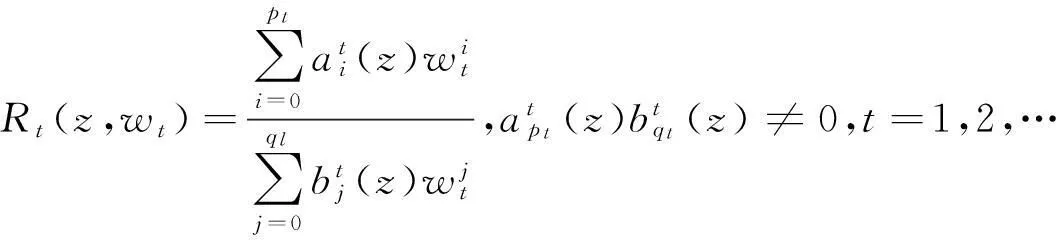
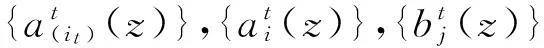
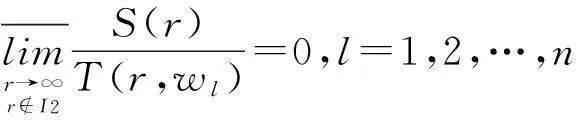
引理3设函数f(z)为复平面上的超越亚纯函数，则对任意的正整数k都有

证明由已知条件和引理2，

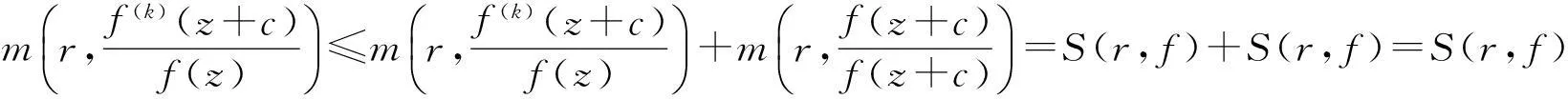
故

引理4设函数f(z)为复平面上的亚纯函数，k是任意的正整数且f(0)=0，f(i-1)(0)=1，f(i)(0)=0 (i=1，2，…，k).则N(r，f(k))≤kN(r，f).

证明由已知，f(k)(z)和f(k-1)(z)以且仅以f(z)的极点为它们的极点.若当f(z)以某点z0为j(j≥1)重极点时，f(k-1)(z)以点z0为k+j-1重极点，f(k)(z)以点z0为k+j重极点.从而

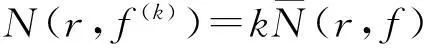
引理5设w1，w2，…，wn都是有限级函数，且T(r，A(i))=o(T(r，wL))，(L=1，2，…，n)，

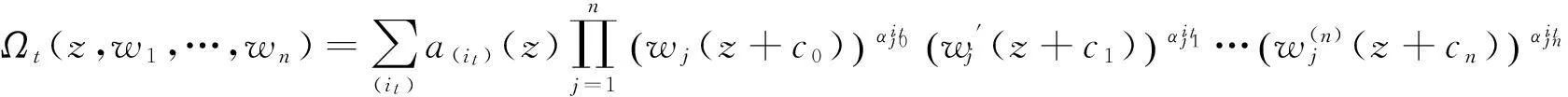
证明定义

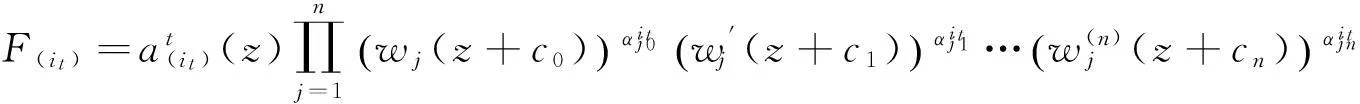
故

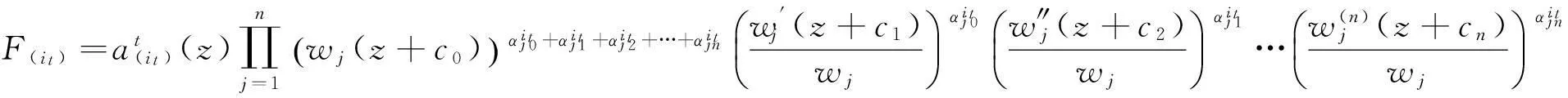
由引理3得

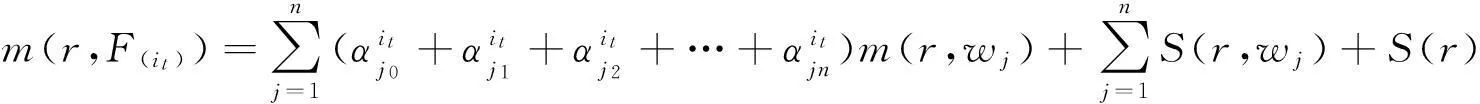
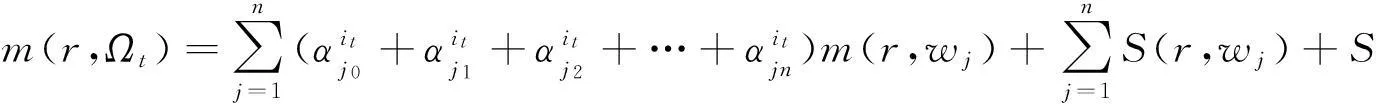
所以

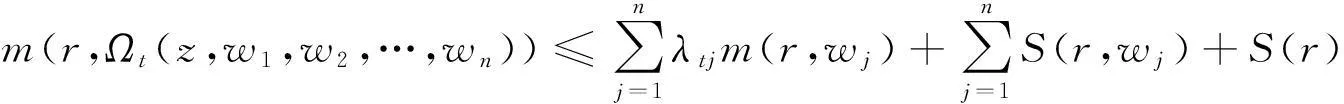
(1.2)

下面估计N(r，Ωt(z，w1，w2…，wn)).由已知和引理2，

N(r，Ω1(z，w1，w2，…，wn))=

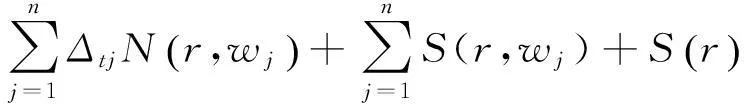
即

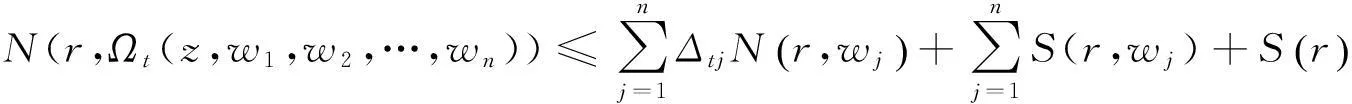
(1.3)

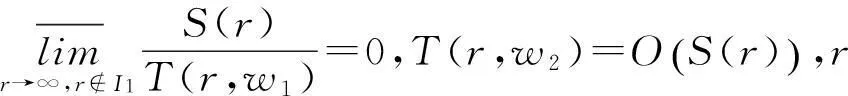
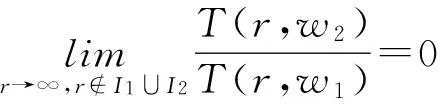
其中I1和I2都是对数测度为有限的例外值集.

证明由已知有

2主要结论

本文利用Nevanlinna值分布理论，对高阶非线性代数微分方程组(1.1)的亚纯允许解的存在性问题进行了研究.根据以上定义以及众多研究的基础上，我们得到以下改进和推广的结论.

定理1设(w1，w2，…，wn)是非线性微分方程组(1.1)的有限级亚纯允许解，则

证明由已知和引理1得：

T(r，R1(z，w1))=max{p1，q1}T(r，w1)+S(r)；

T(r，R2(z，w2))=max{p2，q2}T(r，w2)+S(r)；

⋮⋮

T(r，Rn(z，wn))=max{pn，qn}T(r，w2)+S(r).

(2.1)

由引理5有：

⋮⋮

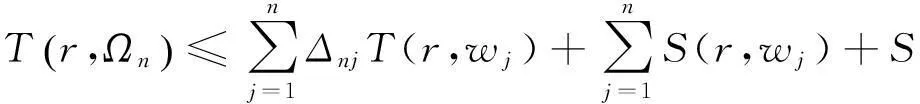
(2.2)

由(1.1)、(2.1)与(2.2)式我们可得：

⋮⋮

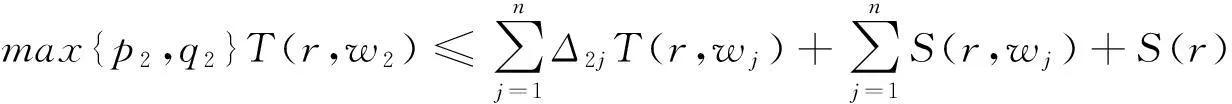
(2.3)

由(2.3)式有：

⋮⋮

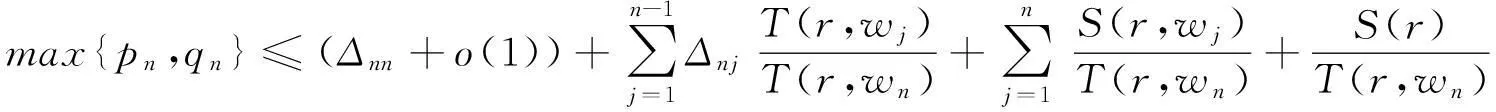
(2.4)

[参考文献]

[2]高凌云.复微分方程组m分量-可允许解[J].数学年刊，1997，18(2):149-154.

[3]高凌云.关于两类复微分方程组的允许解[J].数学学报，2000，43(1):149-156.

[4]高凌云.具有允许解的代数微分方程组的形式[J].系统科学与数学，2004，24(1):96-101.

[5]高凌云.代数微分方程组允许解的值分布[J].系统科学与数学，2007，27(4):629-632.

[6]高凌云.Malmquist型复差分方程组[J].数学学报，2012，55(2):293-300.

[7]王钥，高凌云.关于两类复非线性微分方程的代数体函数解[J].系统科学与数学，2013，33(2):246-254.

[8]高凌云.复高阶差分方程解[J].数学学报，2013，56(4):451-458.

[9]吴桂荣.复域内代数微分方程组的可允许解[J].福建师范大学学报，1992，8(1):16-20.

[10]宋述刚.代数微分方程组的可允许解[J].数学杂志，2008，28(6):685-688.

[11]LAINE I.Nevanlinna theory and complex differential equation [M].Berlin:Walter de Gruyter，1993:18-49.

[12]KORHONEN R.A new clunie type theorem for difference polynomials[J].J difference Equ Appl，2011，17(3):387-400.

[13]杨乐.值分布论及其新研究[M].北京:科学出版社，1982:104-165.

[13]丁勇.一类微分方程组的非可允许分量[J].暨南大学学报，2013，34(1):25-18.

[14]金瑾.关于一类高阶齐次线性微分方程解的增长性[J].中山大学报，2013，52(1):51-55.

[15]金瑾.一类高阶齐次线性微分方程解的增长性[J].华中师范大学报，2013，47(1):4-7.

[16]金瑾.关于高阶线性微分方程解与其小函数的增长性[J].上海交通大学学报(自然科学版)，2013，47(7):1155-1159.

[17]金瑾.单位圆内高阶齐次线性微分方程解与小函数的关系[J].应用数学学报，2014，37(4)：254-264.

[18]金瑾，武玲玲，樊艺.高阶非线性微分方程组的亚纯允许解[J].东北师大学报(自然科学版)，2015，47(1):22-25.

[19]李广兵，唐先华.一类二阶非线性微分积分方程两点边值问题[J].东北师大学报(自然科学版)，2015，47(1):26-30.

(责任编辑：李亚军)

On the meromorphic admissible solution of systems of differential equations

JIN Jin1，2

(1.Department of Mathematics，Guizhou University of Engineering Science，Bijie 551700，China；2.Research Institute of Circular Economy of Bijie，Bijie 551700，China)

Abstract:Using Nevanlinna theory of the value distribution of meromorphic functions，the problem of the existence of solutions on the higher-order nonlinear algebraic differential equation is investigated.It is shown that the meromorphic solution of the differential equations system are all admissible or non admissible.Moreover，some more general results are deduced.

Keywords:differential equations systems；meromorphic function；admissible solution；Nevanlinna theory；value distribution

[文章编号]1000-1832(2016)02-0027-04

[收稿日期]2014-10-15

[基金项目]贵州省科学技术基金资助项目(2010GZ43286，2012GZ10526)；贵州省毕节市科研基金资助项目 ([2011]02)；贵州省教育厅科学技术基金重点资助项目([2015]392).

[作者简介]金瑾(1962—)，男，教授，主要从事复分析研究.

[中图分类号]O 174.52[学科代码]110·41

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.007