半群K(n，r)的生成集

瞿云云，赵　平，游泰杰

(贵州师范大学数学科学学院，贵州 贵阳 550001)

半群K(n，r)的生成集

瞿云云，赵平，游泰杰

(贵州师范大学数学科学学院，贵州 贵阳 550001)

[摘要]设Tn是有限集xn上的全变换半群，对任意的1≤r≤n，令K(n，r)={α∈Tn|rank(α)≤r}，则其为Tn的一个子半群.研究了半群K(n，r)中秩为r的元素组成的集合的任意子集g构成K(n，r)生成集的充分必要条件.

[关键词]变换半群；生成集；图

0引言

变换半群一直被人们研究并关注着.[1-10]类似于对称群Sx，我们将一个有限或无限集合x上的全变换半群记为Tx，本文仅讨论有限集x=xn={1，…，n} 的情形.引入以下记号：用Tn与Sn分别表示Txn与Sxn；TnSn是由xn上的奇异变换所构成的半群，称为奇异变换半群，记为Sinɡn；设α∈Tn，用im(α)与rank(α)分别表示变换α的像集及像集的元素个数；α的核定义为

ker(α)={(x，y)∈xn×xn|xα=yα}.

Tn中的格林关系刻画如下：对于任意的α，β∈Tn，

(α，β)∈R⟺ker(α)=ker(β)；

(α，β)∈L⟺im(α)=im(β)；

(α，β)∈D⟺rank(α)=rank(β).

半群Tn有n个D-类:D1，D2，…，Dn，其中Dr={α∈Tn|rank(α)=r}.对任意的1≤r≤n，令

K(n，r)={α∈Tn|rank(α)≤r}，

则K(n，r)=D1∪…∪Dr，K(n，r)显然是Tn的双边理想，且是Tn的正则子半群.

设S是一个半群且g是S的一个非空子集.S包含g的最小子半群称为由g生成的子半群，记为〈g〉.设g是半群S的一个子集，如果〈g〉=S，则称g是S的一个生成集.在半群研究中，一个自然的问题就是怎样描述半群的(最小)生成集.Howie[11]证明了Singn是由秩为n-1的幂等元所生成的，并且与Gomes[6]共同证明了当n≥3时Singn的一个最小生成集包含n(n-1)/2个秩为n-1的元素；AyIk等[7]给出了秩为n-1的元素组成的集合构成Singn的一个(最小)生成集的充分必要条件；Evseev等[8]证明了K(n，r)(1≤r≤n-1)是由秩为r的幂等元所生成的.本文给出了K(n，r)中秩为r的元组成的集合构成K(n，r)的一个(最小)生成集的充分必要条件.

给定Tn的一个子集u，用E(u)表示子集u所有幂等元组成的集合.本文未定义的符号及术语请参见文献[12-13].

1预备知识

设在图Γ中，所有边的集合为E(Γ)，所有顶点的集合为v(Γ).如果对任意的两个顶点u，v∈v(Γ)，u≠v，满足边(u，v)∈E(Γ)或者边(v，u)∈E(Γ)，则称图Γ是完全的；在图Γ中，如果对于Γ中的顶点{v0，v1，…，vn}满足(vi-1，vi)∈E(Γ)(1≤i≤n)，则称之为v0到vn的一条路径；对于图Γ中的两个顶点u，v∈v(Γ)，如果存在从u到v的一条路径，则称在Γ图中u是连接到v的；如果对于任何的两个顶点u，v∈v(Γ)，在图Γ中u都是连接到v的，则称图Γ是强连接的.

S(n，1)=S(n，n)=1，S(n，r)=S(n-1，r-1)+rS(n-1，r).

设A∈Λr且α∈Dr.如果对任意的x，y∈A，xα≠yα，则称A是α的一个横截集，记为A#α.

定义ΓG(r)如下:

(1)ΓG(r)的顶点集是g，记为v=v(ΓG(r))；

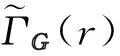
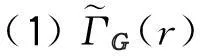
引理1设α，β∈Dr.则αβ∈Dr，当且仅当im(α)#β.

引理2[12]对于半群S中的两个元素A与b，ab∈RA∩Lb，当且仅当E(Rb∩LA)≠∅.

2主要结果

定理1设g是Dr的一个子集.则g是K(n，r)的一个生成集，当且仅当对于每个ε∈E(Dr)，存在α，β∈g，使得：

(ⅰ)αRεLβ；

(ⅱ)在图ΓG(r)中，α是连接到β的.

证明必要性.设g是K(n，r)的一个生成集，则对于每个ε∈E(Dr)，存在α1，α2，…，αs∈g使得

ε=α1α2…αs.

由α1，α2，…，αs，ε∈Dr，α1RεLαs且αkαk+1∈Dr(1≤k≤s-1).由引理1可知im(αk)#αk+1，故在图ΓG(r)中存在一条路径从α1连接到αs，令α1=α，αs=β，则必要性得证.

充分性.因为K(n，r)中的每一个元素都可写成Dr幂等元的乘积，故只需证明E(Dr)⊆〈g〉.设ε∈E(Dr)，由结论(ⅰ)可知存在α，β∈g使得αRεLβ；从结论(ⅱ)可知存在一条路径连接α到β，为

α=α1→α2→…→αs-1→αs=β，

则im(αk)#αk+1(1≤k≤s-1)，从而im(α1…αk+1)=im(αk+1)(1≤k≤s-1)，im(α1…αs-1)#αs.由引理1可知α1α2…αs∈Dr且α1Rα1α2…αsLαs，由于α=α1，β=αs，αRεLβ，因此α1α2…αsHε.因hε为具有单位元ε的有限群，存在一个正整数m使得ε=(α1α2…αs)m∈〈g〉，由此可得E(Dr)⊆〈g〉，充分性得证.

因为rank(K(n，r))=S(n，r)[14]，K(n，r)具有S(n，r)个元素的生成集是K(n，r)的最小生成集，因此有如下结论.

推论1设g是Dr的具有S(n，r)个元素的子集.则g是K(n，r)的一个最小生成集，当且仅当对于每个ε∈E(Dr)，存在α，β∈g，使得：

(1)αRεLβ；

(2)在图ΓG(r)中，α是连接到β的.

对A，b∈Λr，因Tn是正则的，存在ε∈E(Dr)使得ε∈LA，设α∈Rε∩Lb，则εα=α.由K(n，r)=〈g〉，存在α1，α2，…，αp，β1，β2，…，βq∈g，使得α=α1α2…αp且ε=β1β2…βq.又g⊆Dr，则αLαp，εLβq，从而A=im(ε)=im(βq)，b=im(α)=im(αp).因为αi，βj∈g⊆Dr(1≤i≤p，1≤j≤q)且

β1β2…βqα1α2…αp=εα=α∈Dr，

所以βqα1，αiαi+1∈Dr，其中i=1，2，…，p-1，由引理1得im(βq)#α1，im(αi)#αi+1(1≤i≤p-1)，故存在一条从A到b的路径：

(A，im(α1))，(im(α1)，im(α2))，…，(im(αp-1)，b).

(A0，A1)，(A1，A2)，…，(Am-2，Am-1)，(Am-1，Am)，

其中A0=im(α)，Am=im(ε)，且存在α1，α2，…，αm∈g使得Ai=im(αi)(1≤i≤m)且Ai#αi+1(0≤i≤m-1)，因此im(αα1…αk)=im(αk)(1≤k≤m)，且im(αα1…αk)#αk+1(1≤k≤m-1)，再根据引理1可知ɡ=αα1…αm∈Dr，αRɡLαm.由于ker(α)=ker(ε)=π且im(αm)=im(ε)=Am⟹αRεLαm，则有ɡHε.注意到hε是一个带单位元ε的有限群，存在一个正整数m使得ε=ɡm∈〈g〉，从而E(Dr)⊆〈g〉.

同样地，由于rank(K(n，r))=S(n，r)，K(n，r)具有S(n，r)个元素的生成集是K(n，r)的最小生成集，因此有如下推论.

设g是E(Dn-1)的一个非空集合.与文献[7]类似，定义图ΓG如下：

(1)ΓG的顶点集是g，记为v(ΓG)；

对α，β∈Dn-1，容易得到Def(α)⊆Ker(β)⟺im(α)#β，从而图ΓG和图ΓG(n-1)是相同的.设ε∈E(Dn-1)，存在i，j∈xn(i≠j)使得ε=ξi，j，容易证明αRε(=ξi，j)Lβ⟺ker(α)=ker(ξi，j)，im(β)=im(ξi，j)⟺Ker(α)={i，j}且Def(β)={i}.因此在定理1中取r=n-1，则有如下推论.

推论3设g是Dn-1的一个子集.则g是Singn的一个生成集，当且仅当对于每一ξi，j∈E(Dn-1)，存在α，β∈g使得：

(1)Ker(α)={i，j}；

(2)Def(β)={i}；

(3)在图ΓG中，α是连接到β的.

经比较发现，文献[7]中的主要结果与推论3完全相同，因此定理1推广了文献[7]的主要结论.

[参考文献]

[1]HOWIE J M.The subsemigroup generated by the idempotents of a full transformation semigroup[J].J London Math Soc，1966，1(1):707-716.

[2]KEARNES K A，SZENDREI，WOOD J.Generating singular transformations[J].Semigroup Forum，2001，63(3):441-448.

[3]ANDRÉ J M.Semigroups that contain all singular transformations[J].Semigroup Forum，2004，68(2):304-307.

[4]AYIK G，AYIK H，HOWIE J M.On factorisations and generators in transformation semigroup[J].Semigroup Forum，2005，70(2):225-237.

[5]AYIK G，AYIK H，HOWIE J M，et al.Rank properties of the semigroup of singular transformations on a finite set[J].Commun Algebra，2008，36(7):2581-587.

[6]GOMES G M S，HOWIE J M.On the ranks of certain finite semigroups of transformations[J].Math Proc Cambridge Phil Soc，1987，101(3):395-403.

[7]AYIK G，AYIK H，BUGAY L，et al.Generating sets of finite singular transformation semigroups[J].Semigroup Forum，2012，86(1):59-66.

[8]EVSEEV A E，PODRAN N E.Semigroups of transformations generated by idempotents of given defect[J].Izv Vysebn Saved Mat，1972，117(2):44-50.

[9]赵颐，游泰杰，赵平.半群PORn理想的极大正则子半群[J].东北师大学报(自然科学版)，2015，47(3):44-48.

[10]吴江燕，游泰杰.保序部分变换半群POn的平方幂等元 [J].东北师大学报(自然科学版)，2015，47(1):6-11.

[11]HOWIE J M.Idempotent generators in finite full transformation semigroups[J].Proc Roy Soc Edinburgh Sect A，1978，81(3/4):317-323.

[12]CLIFFORD H，PRESTON G B.The algebraic theory of semigroups[M].Providence：American Math Soc，1961：-.

[13]HOWIE J M.Fundamentals of semigroup theory[M].Oxford：The Clarendon Press，1995:341-343.

[14]HOWIE J M，MCFADDEN R B.Idempotent rank in finite full trasformation semigroup[J].Proc Roy Soc Edinburgh Sect A，1990，114:161-167.

(责任编辑：李亚军)

Generating sets of the semigroup K(n，r)

QU Yun-yun，ZHAO Ping，YOU Tai-jie

(School of Mathematics Science，Guizhou Normal University，Guiyang 550001，China)

Abstract:Let Tn be the full transformation semigroup on a finite set Xn.For 1≤r≤n，let K(n，r)={α∈Tn|rank(α)≤r}，which is an subsemigroup of Tn.Necessary and sufficient conditions are founded to keep the set constructed by the transformations of rank r to be a(minimal)generating set for the semigroup K(n，r).

Keywords:tramformation semigroup; generating set; digraph

[文章编号]1000-1832(2016)02-0023-04

[收稿日期]2014-02-24

[基金项目]国家自然科学基金资助项目(11461014)；贵州省科学技术基金资助项目(黔科合J字[2013]2225).

[作者简介]瞿云云(1983—)，男，硕士，副教授，主要从事代数与密码学研究；通讯作者：赵平(1973—)，男，硕士，教授，主要从事半群代数理论研究.

[中图分类号]O 157.1[学科代码]110·21

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.006