强α-弱对称环

薛　岭，王　尧，任艳丽

(1.南京信息工程大学数学与统计学院，江苏 南京 210044；2.南京晓庄学院数学与信息技术学院，江苏 南京 211171)

强α-弱对称环

薛岭1，王尧1，任艳丽2

(1.南京信息工程大学数学与统计学院，江苏 南京 210044；2.南京晓庄学院数学与信息技术学院，江苏 南京 211171)

[摘要]引进了强α-弱对称环的概念并研究其基本性质，讨论了强α-弱对称环与弱对称环、强α-弱半交换环等相关环的关系，给出强α-弱对称环的一些扩张性质，得到了判定强α-弱对称环的几个充要条件.

[关键词]强α-弱对称环;强α-弱半交换环;弱α-相容环;NI环;斜多项式环

1预备知识

本文讨论的环R都是有单位元的结合环，α是环R的一个非零自同态.称一个环R为α-rigid环，是指对任意的r∈R，由rα(r)=0可以推出r=0；称R为约化环，是指R没有非零幂零元；称R为对称环，是指对任意的A，b，c∈R，由abc=0可以推出acb=0；称R为可逆环，是指对任意的A，b∈R，由ab=0可以推出ba=0；称R为半交换环，是指对任意的A，b∈R，由ab=0可以推出aRb=0.

α-rigid环是约化环，约化环是对称环，对称环是可逆环，可逆环是半交换环.如果将α-rigid环、对称环、可逆环和半交换环的概念按某些方向进行推广，可以得到一系列新的环.例如，称一个环R是弱α-rigid环，如果对任意的A∈R，由aα(A)∈nil(R)可以推出A∈nil(R)；称一个环R是弱对称环，如果对任意的A，b，c∈R，由abc∈nil(R)可以推出acb∈nil(R)；[1]称一个环R是诣零半交换环，如果对任意的A，b∈R，由ab∈nil(R)可以推出aRb⊆nil(R)；称一个环R是α-相容的，如果对任意的A，b∈R，ab=0，当且仅当aα(b)=0；称一个环R是弱α-相容环，如果对任意的A，b∈R，ab∈nil(R)，当且仅当aα(b)∈nil(R).此外，文献[2-3]分别研究了具有弱对称自同态的环和具有自反自同态的环.

近年来，许多文章讨论具有其他自同态性质的环.Kwak[4]称一个环R的自同态α是右(左)对称的，如果对任意的A，b，c∈R，由abc=0可以推出acα(b)=0(α(b)ac=0);称一个环R是右(左)α-对称环，如果α是环R的右(左)对称同态；如果环R既是右α-对称环，也是左α-对称环，则称环R是α-对称环.Baser，Hong和Kwak[5]称环R的一个自同态α是右(左)可逆的，如果对任意的A，b∈R，由ab=0可以推出bα(A)=0(α(b)A=0);称环R是右(左)α-可逆的，如果α是环R的右(左)可逆同态；如果环R既是右α-可逆环，也是左α-可逆环，则称环R是α-可逆环.Baser和Kwak[6]称一个环R是右(左)α-半交换环，如果对任何A，b∈R，由ab=0可以推出aRα(b)=0(α(A)Rb=0);如果环R既是右α-半交换环，也是左α-半交换环，则称环R是α-半交换环.α-rigid环是α-对称环，α-对称环是α-可逆环，也易知α-对称环是α-半交换环.[6]

同时，还有学者讨论具有相反性质的自同态的环.Baser和Kwak[7]称一个环R是强右(左)α-可逆环，如果对任意A，b∈R，由aα(b)=0(α(A)b=0)可以推出ba=0;如果一个环R既是强右α-可逆环，也是强左α-可逆环，则称环R是强α-可逆环.强α-可逆环是α-可逆环，但α-可逆环未必是强α-可逆环，可逆环也未必是强α-可逆环.[7]文献[8]称环R是强右(左)α-对称环，如果对任意A，b，c∈R，由abα(c)=0(α(A)bc=0)可以推出acb=0(bac=0);如果一个环R既是强右α-对称环，也是强左α-对称环，则称环R是强α-对称环.一个强右(左)α-对称环一定是对称环，而且强右α-对称环和强左α-对称环两个概念是等价的.[8]

本文提出强α-弱对称环的概念，研究它与相关环的关系，给出其若干性质.

2强α-弱对称环和强α-弱半交换环

定义2.1设α是环R的一个自同态.称α是强右(左)弱对称的，如果对任意A，b，c∈R，由abα(c)∈nil(R)(α(A)bc∈nil(R))可以推出acb∈nil(R)(bac∈nil(R));称环R是强右(左)α-弱对称环，如果α是环R的强右(左)弱对称的自同态;如果一个环R既是强右α-弱对称环，也是强左α-弱对称环，则称环R是强α-弱对称环.

命题2.1设α是环R的一个自同态，则R是强右α-弱对称环当且仅当R是强左α-弱对称环.

证明设R是强右α-弱对称环.如果对A，b，c∈R，有α(A)bc∈nil(R)，则bcα(A)∈nil(R)，从而bac∈nil(R)，故R也是强左α-弱对称环.同理可知，反之亦然.

命题2.1说明强左α-弱对称环与强右α-弱对称环是同一个概念，于是我们对这两个概念不加区分，统称为强α-弱对称环.

易知强α-对称环是强α-弱对称环.因为弱对称环未必是对称环，所以强α-弱对称环未必是强α-对称环.

当α是恒等自同态时，强α-弱对称环和弱对称环是等价概念，但对于一般的自同态，弱对称环未必是强α-弱对称环.

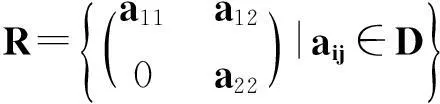
定理2.1环R是一个强α-弱对称环，当且仅当R是弱对称环且是弱α-相容环.

证明必要性.先证环R是弱对称环.设abc∈nil(R)，A，b，c∈R，则有cab∈nil(R)，α(c)α(A)α(b)=α(cab)∈nil(R).由环R是强α-弱对称环，有α(c)bα(A)∈nil(R)，1·bα(ac)∈nil(R)，从而有acb∈nil(R).再证R是弱α-相容环.任取A，b∈R，设ab∈nil(R)，于是ba∈nil(R)，1·α(b)·α(A)=α(ba)∈nil(R).因为R是强α-弱对称环，所以aα(b)∈nil(R).反过来，任取A，b∈R，设aα(b)∈nil(R).由环R是有1的强α-弱对称环，得ba∈nil(R)，所以ab∈nil(R).这就证明了环R是弱α-相容环且R是弱对称环.

充分性.设abα(c)∈nil(R)，A，b，c∈R.由R是一个弱α-相容环有abc∈nil(R).再由R是一个弱对称环有acb∈nil(R).这就证明R是强α-弱对称环.

定义2.2设α是环R的一个自同态.称α是强右(左)弱半交换的，如果对任意的A，b∈R，由aα(b)∈nil(R)(α(A)b∈nil(R))可以推出aRb⊆nil(R)；称环R是强右(左)α-弱半交换环，如果α是环R的强右(左)弱半交换的自同态；如果一个环R既是强右α-弱半交换环，也是强左α-弱半交换环，则称环R是强α-弱半交换环.

命题2.2环R是强右α-弱半交换环，当且仅当R是强左α-弱半交换环.

证明如果R是强右α-弱半交换环，设aα(b)∈nil(R)，A，b∈R.则有bα(A)∈nil(R)，从而bRa⊆nil(R)，ba∈nil(R)，α(b)α(A)=α(ba)∈nil(R).因此α(b)Ra⊆nil(R)，α(b)A∈nil(R)，aα(b)∈nil(R).故aRb⊆nil(R).反之亦然.

由上述命题，我们对强右α-弱半交换环和强左α-弱半交换环不加区分，统称为强α-弱半交换环.

命题2.3环R是强α-弱半交换环，当且仅当R是诣零半交换环，且R是弱α-相容环.

证明必要性.先证R是弱α-相容环.设ab∈nil(R)，A，b∈R，则α(A)α(b)∈nil(R)，于是aRα(b)⊆nil(R)，aα(b)∈nil(R).反过来，设aα(b)∈nil(R)，A，b∈R，从而aRb⊆nil(R)，ab∈nil(R).再证R是诣零半交换环.设ab∈nil(R)，A，b∈R，则aα(b)∈nil(R)，aRb⊆nil(R).

充分性.设aα(b)∈nil(R)，A，b∈R.则ab∈nil(R)，aRb⊆nil(R).

下面，我们探究强α-弱对称环和强α-弱半交换环的关系.由定理2.1和命题2.3，我们首先考虑弱对称环和诣零半交换环的关系.

称一个环R是素环，如果对任意的A，b∈R，由aRb=0可以推出A=0或b=0.Marks[9]称一个环R是NI环，如果nil(R)构成环R的一个理想.

引理2.1[1]设R是一个诣零半交换环.对任意的A1，A2，…，An∈R，如果A1A2…An∈nil(R)，则有A1r1A2r2…An-1rn-1An∈nil(R)，其中r1，r2，…，rn-1∈R，且n≥2.

命题2.4(1)如果一个环R是诣零半交换环，则R是弱对称环；如果R是NI环且是弱对称环，则R是诣零半交换环.

(2)如果一个环R是弱α-相容环，则R是弱α-rigid环；如果R是NI环且是弱α-rigid环，则R是弱α-相容环.

证明(1)如果R是诣零半交换环，设abc∈nil(R)，A，b，c∈R.因为R是有1的诣零半交换环，即abc·1∈nil(R)，从而acbacb·1∈nil(R)，acb∈nil(R).反过来，如果R是NI环且是弱对称环，设ab∈nil(R)，A，b∈R.因为R是NI环，所以对任意的r∈R有abr∈nil(R).再利用弱对称性推出arb∈nil(R)，即aRb⊆nil(R).

(2)如果一个环R是弱α-相容环，设aα(A)∈nil(R)，A∈R，则A2∈nil(R)，A∈nil(R).如果R是NI环且是弱α-rigid环，设ab∈nil(R)，A，b∈R，则α(ab)∈nil(R)，α(α(b)A)α(b)A=α2(b)α(A)α(b)A∈nil(R).而环R是弱α-rigid环，于是α(b)A∈nil(R).

推论2.1(1)如果环R是强α-弱半交换环，则R是强α-弱对称环.

(2)如果R是强α-弱对称环且是NI环，则R是强α-弱半交换环.

证明由定理2.1，命题2.3和命题2.4可得.

命题2.5(1)可逆环是诣零半交换环.

(2)如果R是素环且是诣零半交换环，则R是可逆环.

证明(1)如果R是可逆环，则R是半交换环，从而是诣零半交换环.

(2)设ab=0∈nil(R)，A，b∈R.则aRb⊆nil(R)，即aRbaRb…aRb=0.同时，R也是素环，于是A=0或baRbaRb…aRb=0.进而b=0或baRbaRb…aRba=0.反复利用素环的性质，得出A=0或b=0或ba=0.因此R是可逆环.

3强α-弱对称环的扩张

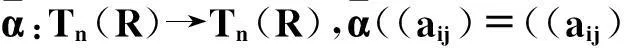
容易验证，强α-弱对称环的α-子环还是强α-弱对称环.

推论3.1下列命题等价:

(1)环R是强α-弱对称环;

证明由R是Δ-1R的α-子环知充分性成立.

命题3.3设α是环R的一个自同态.R[x]是强α-弱对称环，当且仅当R[x;x-1]是一个强α-弱对称环.

证明充分性显然.

必要性.令Δ={1，x，x2，…}，易证Δ是由R[x]的中心正则元组成的乘法封闭子集，且R[x;x-1]=Δ-1R[x].由命题3.2知R[x;x-1]是一个强α-弱对称环.

引理3.1[10]如果环R是Armendariz环，则nil(R)是R的子环.

引理3.2[11]环R是Armendariz环，当且仅当R[x]是Armendariz环.

引理3.3[10]Armendariz环是Nil-Armendariz环.

引理3.4[10]如果环R是Nil-Armendariz环，则R[x]是Nil-Armendariz环，当且仅当nil(R)[x]=nil(R[x]).

引理3.5[11]如果环R是Armendariz环，则对任意的f1，…，fn∈R[x]，由f1…fn=0可以推出A1…An=0，其中Ai是fi系数.

命题3.4设α是环R的一个自同态，如果环R是Armendariz环，则下列结论等价:

(1)R是一个强α-弱对称环;

证明由命题3.3知(2)⟺(3).

(2)⟹(1)显然.

(1)⟹(2).因为环R是Armendariz环，由引理3.1知nil(R)是R的子环，由引理3.2知R[x]是Armendariz环.再根据引理3.3和引理3.4有nil(R)[x]=nil(R[x]).

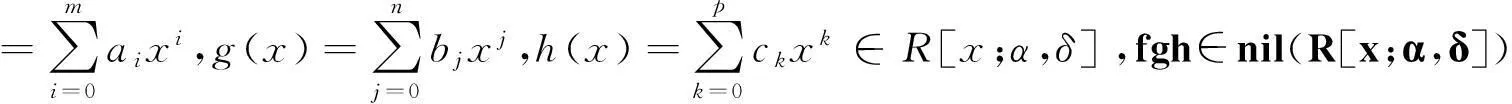
证明充分性显然.

[参考文献]

[1]CHEN WEIXING.On nil-semicommutative rings[J].Thai J Math，2011(1):39-47.

[2]王尧，钱青，任艳丽.具有弱对称自同态的环[J].山东大学学报(理学版)，2014，49(2)：12-17.

[3]王尧，沈青，任艳丽.具有自反条件的环自同态[J].东北师大学报(自然科学版)，2013，45(3)：9-14.

[4]KWAK T K.Extensions of extended symmetric rings[J].Bull Korean Math Soc，2007，44(4)：777-788.

[5]BASER M，HONG C Y，KWAK T K.On extended reversible rings[J].Algebra Colloq，2009，16(1)：37-48.

[6]BASER M，KWAK T K.Extended semicommutative rings[J].Algebra Colloq，2010，17(2)：257-264.

[7]BASER M，KWAK T K.On strong reversible rings and their extensions[J].Korean J Math，2010，18(2)：119-132.

[8]王尧，薛岭，任艳丽.具有强对称自同态的环及其扩张[J].吉林大学学报(理学版)，2014，52(5)：861-868.

[9]MARKS G.On 2-primal ore extensions[J].Comm Algebra，2001，29(5):2113-2123.

[10]ANTOINE R.Nilpotent elements and Armendariz rings[J].Algebra，2008，319：3128-3140.

[11]ANDERSON D，CAMILLO V.Armendariz rings and Gaussian rings[J].Comm Algebra，1998，26:2265-2272.

[12]WANG YAO，WANG WEILIANG，REN YANLI.Rings with symmetric endomorphisms and their extensions[J].J Math Res Appl，2015，35(1)：56-70.

(责任编辑：李亚军)

On strongly α-weak symmetric rings

XUE Ling1， WANG Yao1， REN Yan-li2

(1.School of Mathematics and Statistics，Nanjing University of Information Science and Technology，Nanjing 210044，China;2.School of Mathematics and Information Technology，Nanjing Xiaozhuang University，Nanjing 211171，China)

Abstract:The concept of strongly α-weak symmetric rings is introduced and some of its basic properties are investigated.The relationships between strongly α-weak symmetric rings and related rings such as weakly symmetric，strongly α-weak semicommutative rings are discussed，and some extensions of strongly α-symmetric rings are studied.Some necessary and sufficient conditions are given to judge α-weak symmetric ring.

Keywords:strongly α-weak symmetric ring；strongly α-weak semicommutative ring；weakly α-compatible ring；NI ring；skew polynomial ring

[文章编号]1000-1832(2016)02-0014-05

[收稿日期]2014-12-29

[基金项目]国家自然科学基金资助项目(41275117)；江苏省自然科学基金资助项目(BK20141476).

[作者简介]薛岭(1990—)，男，硕士，主要从事结合环和结合代数研究；通讯作者：任艳丽(1965—)，女，硕士，教授，主要从事环论研究.

[中图分类号]O 153.3[学科代码]110·2104

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.004