一类双色代数的构造

王　涵，那惠欣，张庆成

(东北师范大学数学与统计学院，吉林 长春 130024)

一类双色代数的构造

王涵，那惠欣，张庆成

(东北师范大学数学与统计学院，吉林 长春 130024)

[摘要]引入了Novikov色代数和Gel’fand-Dorfman双色代数的概念，构造了三类Gel’fand-Dorfman双色代数.

[关键词]李代数；Novikov色代数；Gel’fand-Dorfman双色代数

李色代数是李代数和李超代数的自然推广，近年来逐渐成为数学家和物理学家感兴趣的课题并得到了许多研究成果.[1-11]共形超代数在弦理论和共形场理论中起着基本作用，文献[12-15]系统地研究了共形超代数，得到其结构、分类和表示的一系列成果.文献[13]研究了二次共形超代数的分类，并证明了二次共形超代数和超Gel’fand-Dorfman双代数是等价的，同时指出这类代数的彻底分类仍是一个挑战.受文献[15]的启发，我们把二次共形超代数推广到更一般的情形，在一般情形下给出了Novikov色代数和Gel’fand-Dorfman双色代数的概念，构造了三类Gel’fand-Dorfman双色代数，有助于我们了解这类代数的结构.

1Novikov色代数

设f是一个域，g是一个交换群，映射ε:g×g→f被称为g上的反对称特征标，如果下列条件成立：

ε(f，g+h)=ε(f，g)ε(f，h)，f，g，h∈g；

(1)

ε(g+h，f)=ε(g，f)ε(h，f)，f，g，h∈g；

(2)

ε(g，h)ε(h，g)=1，g，h∈g.

(3)

不难得到，对任意的g∈g，ε(g，g)=±1，可以把g分解成两个子集合：

g+={g∈g|ε(g，g)=1}；

g-={g∈g|ε(g，g)=-1}.

显然g+是g的一个子群.当g被定义了反对称特征标时，一个g-阶化代数(或者一个g-阶化向量空间)被称为一个色代数(或者色向量空间).本文涉及的理想，子空间，子模都是色的.

[u，v]=-ε(u，v)[v，u]，

(4)

ε(w，u)[u，[v，w]]+ε(u，v)[v，[w，u]]+ε(v，w)[w，[u，v]]=0.

(5)

其中所有的元素都是齐次的，并且u，v，w∈L，ξ，η∈g.特别地，g={1，g}≅Z2和ε(g，g)=-1给出了一个通常的李超代数.

(u∘v)∘w=ε(v，w)(u∘w)∘v，

(6)

(u，v，w)=ε(u，v)(v，u，w).

(7)

其中(u，v，w)=(u∘v)∘w-u∘(v∘w)，u，v，w∈A，ξ，η∈g.

例1.1如果g={0}，即ε(0，0)=1，则每一个Novikov代数都是Novikov色代数.

例1.3设A是一个色交换代数，满足

u∘v=ε(u，v)v∘u.

则A是一个Novikov色代数.

定义1.2设A是一个Novikov色代数，h是A的一个g-阶化向量空间，满足

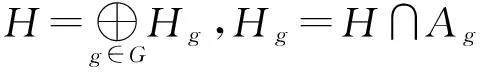
其中g∈g.

(1)如果对所有的x∈A，y∈h，我们有x∘y∈h，y∘x∈h，则称h为A的一个Novikov色子代数.

(2)如果h∘A⊂h，A∘h⊂h，则称h为A的一个Novikov色理想.

定义1.3设A是Novikov色代数，∂∈(EndA)η，η∈g.如果∂(Aξ)⊂Aξ+η，且

∂(u∘v)=∂(u)∘v+ε(u，v)u∘∂(v)，ε，η∈g，

则∂被称为次数为η的色导子；如果η∈g+，则称∂是一个偶导子；如果η∈g-，我们称η为奇导子.

对于Novikov色代数(A，∘)，我们在A上定义运算[·，·]：

[A，b]=A∘b-ε(A，b)b∘A，A，b∈A.

(8)

2Gel’fand-Dorfman双色代数

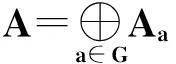
[w∘u，v]-ε(u，v)[w∘v，u]+[w，u]∘v-ε(u，v)[w，v]∘u-w∘[u，v]=0，u，v，w∈A.

(9)

定理2.1设(A，∘)是一个Novikov色代数.则(A，[·，·]，∘)(见(8)式)是一个Gel’fand-Dorfman双色代数.

证明不难验证(A，[·，·]，∘)是一个李色代数.对u，v，w∈A，利用(6)─(7)式有

[w∘u，v]-ε(u，v)[w∘v，u]+

[w，u]∘v-ε(u，v)[w，v]∘u-w∘[u，v]=

(w∘u)∘v-ε(u+w，v)v∘(w∘u)-ε(u，v)(w∘v)∘u+

ε(w，u)u∘(w∘v)+(w∘u)∘v-

ε(w，u)(u∘w)∘v-ε(u，v)(w∘v)∘u+

ε(u+w，v)(v∘w)∘u-w∘(u∘v)+ε(u，v)w∘(v∘u)=

-ε(u+w，v)v∘(w∘u)+ε(w，u)u∘(w∘v)-ε(w，u)(u∘w)∘v+

ε(u+w，v)(v∘w)∘u+ε(u，v)w∘(v∘u)-w∘(u∘v)=

ε(u+w，v)((v∘w)∘u-v∘(w∘u))-

ε(w，u)((u∘w)∘v-u∘(w∘v))-

w∘(u∘v)+ε(u，v)w∘(v∘u)=

ε(u+w，v)(v，w，u)-ε(w，u)(u，w，v)-

w∘(u∘v)+ε(u，v)w∘(v∘u)=

ε(u，v)(w，v，u)-(w，u，v)-w∘(u∘v)+ε(u，v)w∘(v∘u)=

ε(u，v)(w∘v)∘u-ε(u，v)w∘(v∘u)-(w∘u)∘v+

w∘(u∘v)-w∘(u∘v)+ε(u，v)w∘(v∘u)=0，

从而(9)式成立.

设A是一个色交换结合代数.用w(A)表示A的导子代数的集合，在w(A)上定义括积[·，·]为

[∂1，∂2]=∂1∂2-ε(∂1，∂2)∂2∂1，

(10)

(ad)(v)=ad(v)(A，v∈A，d∈w(A))

(11)

构成一个左A-模.

令N=w(A)⨁A，在N上定义代数运算[·，·]，“∘”如下:

[d1+ξ1，d2+ξ2]=[d1，d2]+d1(ξ2)-ε(d1，d2)d2(ξ1)，

(12)

(d1+ξ1)∘(d2+ξ2)=ε(d1，d2)ξ2d1+ξ1ξ2，

(13)

其中d1+ξ1，d2+ξ2∈N.

定理2.2代数(N，[·，·]，∘)是一个Gel’fand-Dorfman双色代数.

证明不难验证(N，[·，·]，∘)是一个李色代数.设di+ξi∈N，i=1，2，3，有

((d1+ξ1)∘(d2+ξ2))∘(d3+ξ3)=(ε(d1，d2)ξ2d1+ξ1ξ2)∘(d3+ξ3)=

ε(d1，d2)ε(d1+d2，d3)ξ3ξ2d1+ξ1ξ2ξ3，

(14)

ε(d2，d3)((d1+ξ1)∘(d3+ξ3))∘(d2+ξ2)=

ε(d2，d3)(ε(d1，d3)ξ3d1+ξ1ξ3)(d2+ξ2)=

ε(d2，d3)(ε(d1，d3)ε(d1+d3，d2)ξ2ξ3d1+ξ1ξ3ξ2)=

ε(d1+d2，d3)ε(d1+d3，d2)ε(d2，d3)ξ3ξ2d1+ε(d2，d3)ξ1ξ3ξ2=

ε(d1，d2)ε(d1+d2，d3)ξ3ξ2d1+ξ1ξ2ξ3.

(15)

上面两个表达式意味着结合性

((d1+ξ1)∘(d2+ξ2))∘(d3+ξ3)=

ε(d2+d3)((d1+ξ1)∘(d3+ξ3))∘(d2+ξ2)，

(16)

而且有

((d1+ξ1)∘(d2+ξ2))∘(d3+ξ3)-(d1+ξ1)∘((d2+ξ2)∘(d3+ξ3))=

(ε(d1，d2)ξ2d1+ξ1ξ2)∘(d3+ξ3)-(d1+ξ1)∘(ε(d2，d3)ξ3d2+ξ2ξ3)=

ε(d1，d2)ε(d1+d2，d3)ξ3ξ2d1)-ε(d2，d3)ε(d1，d2+d3)ξ2ξ3d1=

ε(d1，d2+d3)ξ2ξ3d1(1-ε(d2，d3))，

(17)

ε(d2，d3)[((d1+ξ1)∘(d3+ξ3))∘(d2+ξ2)-(d1+ξ1)∘((d3+ξ3)∘(d2+ξ2))]=

ε(d2，d3)ε(d1，d3)ε(d1+d3，d2)ξ2ξ3d1-ε(d2，d3)ε(d1，d2+d3)ε(d3，d2)ξ2ξ3d1=

ε(d1，d2+d3)ξ2ξ3d1-ε(d1，d2+d3)ε(d2，d3)ξ2ξ3d1=

ε(d1，d2+d3)ξ2ξ3d1(1-ε(d2，d3)).

(18)

(17)─(18)式证明了(7)式中的第二个等式成立，因此(N，∘)是一个Novikov色代数.

下面我们验证相容性条件成立.

[(d3+ξ3)∘(d1+ξ1)，d2+ξ2]-

ε(d1，d2)∘[(d3+ξ3)∘(d2+ξ2)，d1+ξ1]+

[d3+ξ3，d1+ξ1]∘(d2+ξ2)-

ε(d1，d2)[d3+ξ3，d2+ξ2]∘(d1+ξ1)-

(d3+ξ3)∘[d1+ξ1，d2+ξ2]=

[ε(d1，d3)ξ3d3+ξ3ξ1，d2+ξ2]-

ε(d1，d2)∘[ε(d2，d3)ξ2d3+ξ3ξ2，d1+ξ1]+

([d3，d1]+d3(ξ1)-ε(d1，d3)d1(ξ3))∘(d2+ξ2)-

ε(d1，d2)∘([d3，d2]+d3(ξ2)-ε(d2，d3)d2(ξ3))∘(d1+ξ1)-

(d3+ξ3)∘([d1，d2]+d1(ξ2)-ε(d1，d2)d2(ξ1))=

ε(d1，d3)ξ1[d3，d2]-ε(d1，d3)(d2，d1+d3)d2(ξ1)d3+

ε(d1，d3)ξ1d3(ξ2)-ε(d2，d1+d3)d2(ξ3ξ1)-

ε(d2，d1+d3)ξ2[d3，d1]+ε(d3，d1+d2)d1(ξ2)d3-

ε(d2，d1+d3)ξ2d2(ξ1)+ε(d1，d3)d1(ξ3ξ2)+

ε(d2，d1+d3)ξ2[d3，d1]+(d3(ξ1)-ε(d1，d3)d1(ξ3))ξ2-

ε(d1，d3)ξ1[d3，d2]-ε(d1，d2)(d3(ξ2)-ε(d2，d3)d2(ξ3))ξ1-

ε(d3，d1+d2)d1(ξ2)d3+ε(d1，d3)ε(d2，d1+d3)d2(ξ1)d3-

ξ3d1(ξ2)+ε(d1，d3)ξ3d2(ξ1)=0.

定义2.2一个李Poisson色代数A是一个g-阶化向量空间有两种代数运算∘和[·，·]，使得(A，∘)是一个色交换结合代数，(A，[·，·])是一个李色代数，并满足相容性条件

[u，v·w]=[u，v]·w+ε(u，v)v·[u，w]，u，v，w∈A.

(19)

设(A，[·，·])是一个Poisson色代数，w(A)是A的导子空间.假设d∈w(A)0满足

d[u，v]=[d(u)，v]+[u，d(v)]+ξ[u，v]，u，v∈A，

(20)

其中ξ∈f是一常数.现在我们在A上定义一个新的代数运算·如下:

u·v=u∘d(v)+ξu∘v，u，v∈A.

(21)

定理2.3代数(A，[·，·]，·)是一个Gel’fand-Dorfman双色代数.

证明对于u，v，w∈A，有

(u·v)·w=(u∘d(v)+ξu∘v)·w=(u∘d(v))·w+ξ(u∘v)·w=

(u∘d(v))∘d(w)+ξ(u∘d(v))∘w+ξ(u∘v)∘d(w)+ξ2(u∘v)∘w，

ε(v，w)(u·w)·v=ε(v，w)(u∘d(w)+ξu∘v)·v=

ε(v，w)((u∘d(w))∘d(v)+ξ(u，d(w))∘v+ξ(u∘w)∘d(v)+ξ2(u∘w)∘v=

(u∘d(v))∘d(w)+ξ(u，d(v))∘w+ξ(u∘v)∘d(w)+ξ2(u∘v)∘w，

从而(6)式成立.可以类似证明(7)式的正确性，因此(A，·)是一个Novikov色代数.

进一步，对于u，v，w∈A，有

[w·u，v]-ε(u，v)[w·v，u]+

[w，u]·v-ε(u，v)[w，v]·u-w·[u，v]=

[w∘(d+ξ)(u)，v]-ε(u，v)[w∘(d+ξ)(v)，u]+

[w，u]∘(d+ξ)(v)-ε(u，v)[w，v]∘(d+ξ)(u)-w∘(d+ξ)[u，v]=

[w∘d(u)，v]-ε(u，v)[w∘d(v)，u]+[w，u]∘d(v)-

ε(u，v)[w，v]∘d(u)+ξ([w∘u，v]-ε(u，v)[w∘v，u]+

[w，u]∘v-ε(u，v)[w，v]∘u)-w∘([d(u)，v]+[u，d(v)]+2ξ[u，v])=0.

因此(A，[·，·]，·)是一个Gel’fand-Dorfman双色代数.

[参考文献]

[1]SCHEUNET M.Generalized Lie algebras[J].J Math Phys，1979，20:712-720.

[2]SCHEUNET M，ZHANG R.Cohomology of Lie superalgebras and theirgeneralizations[J].J Math Phys，1998，39：5024-5061.

[3]WILSON M.Delta methods in enveloping algebras of Lie colour algebras[J].J Algebra，1995，175：661-696.

[4]PRICE K.Primeness criteria for universal enveloping algebras of Lie color algebras[J].J Algebra，2001，235：589-607.

[5]PASSMAN D.Simple Lie color algebras of Witt type[J].J Algebra，1998，208：698-721.

[6]SU Y，ZHAO K，ZHU L.Simple Lie colour algebras of Weyl type[J].Israel J Math 2003，137：109-123.

[7]FELDVOSS J.Representations of Lie colour algebras[J].Adv Math，2001，157：95-137.

[8]ZHANG Q，ZHANG Y.Derivations and extensions of Lie color algebra[J].Acta Mathematica Scientia，2008，28B：933-948.

[9]BAHTURIN Y，MIKHALEV A，PETROGRADSHY V，et al.Infinite dimensional Lie superalgebras[M].Boston：De Gruyter，1992:7-15.

[10]宋华，王晨迪.李Color 代数极大子代数的基本性质[J].东北师大学报(自然科学版)，2012，44：26-30.

[11]马凤敏，张永平，董蕾，等.三维Hom-Leibniz超代数的分类[J].东北师大学报(自然科学版)，2014，46：1-8.

[12]GEL’FAND I，DORFMAN I.Hamiltonian operators and infinite-dimensional Lie algebras[J].Functional Analysis and Its Applications，1981，14：23-40.

[13]XU X.Quadratic conformal superalgebras[J].J Algebra，2000，231：1-38.

[14]XU X.Intertwining operators for twisted modules of colored vertex operator superalgebra[J].J Algebra，1995，175：241-273.

[15]XU X.Simple conformal superalgebras of finite growth[J].Algebra Colloquium，2000，7(2)：205-240.

(责任编辑：李亚军)

The structure of a kind of double color algebra

WANG Han，NA Hui-xin，ZHANG Qing-cheng

(School of Mathematics and Statistics，Northeast Normal University，Changchun，130024，China)

Abstract:The concepts of Novikov color algebra and color Gel’fand-Dorfman double algebra are introduced.Meanwhile，three types of color Gel’fand-Dorfman double algebra are constructed.

Keywords:Lie algebra；Novikov color algebra；color Gel’fand-Dorfman double algebra

[文章编号]1000-1832(2016)02-0001-05

[收稿日期]2014-10-21

[基金项目]国家自然科学基金资助项目(11471090);吉林省自然科学基金资助项目(20130101068JC).

[作者简介]王涵(1990—)，女，硕士，主要从事李理论研究；通讯作者:张庆成(1960—)，男，博士，教授，主要从事李理论研究.

[中图分类号]O 152.5[学科代码]110·2130

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.001