解析函数空间上的有限秩加权复合算子

赵 连 阔

(山西师范大学数学与计算机科学学院，山西 临汾 041004)

·研究简报·

解析函数空间上的有限秩加权复合算子

赵 连 阔

(山西师范大学数学与计算机科学学院，山西 临汾 041004)

[摘要]给出了解析函数再生核巴拿赫空间上有限秩加权复合算子的统一刻画.主要结论表明解析函数再生核巴拿赫空间上的有限秩加权复合算子或者是零算子或者是一秩算子.

[关键词]解析函数空间；加权复合算子；有限秩

1预备知识

设Ω是复空间CN中的域，h(Ω)表示Ω上解析函数全体构成的集合.记x为由Ω上解析函数构成的具有再生核的巴拿赫空间，且包含所有解析多项式.x具有再生核是指对任意w∈Ω，在点w的取值泛函有界，即存在x上的连续线性泛函δw使得δw(f)=f(w)，f∈x.熟知的单圆盘上的哈代空间，复平面上的Fock空间等都是再生核解析函数巴拿赫空间.关于再生核函数空间的基本知识参见文献[1-2].

设ψ∈h(Ω)，φ是Ω上的解析自映射，定义算子Cψ，φ:x→x如下：

(Cψ，φf)(z)=ψ(z)f(φ(z))，z∈Ω，f∈x.

则称Cψ，φ为x上的加权复合算子.加权复合算子是一类非常重要的具体算子，可看作是乘法算子和复合算子的结合，其基本问题是通过定义符号ψ和φ的函数性质来反映加权复合算子Cψ，φ的算子性质，如算子的有界性、紧性、可逆性等.各类函数空间上的加权复合算子已经得到广泛且深入的研究.[3-7]在函数空间上，加权复合算子与Toeplitz算子[8]、积分算子[9]一样重要.

2主要结论

定理1设ψ∈h(Ω)，ψ≠0，φ是Ω上的解析自映射.则Cψ，φ是x上的有限秩算子，当且仅当ψ∈x且存在b∈Ω使得φ(z)=b.换句话说，Cψ，φ是x上的非零有限秩算子，当且仅当Cψ，φ是x上的一秩算子.

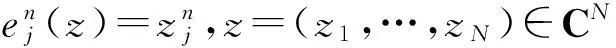
充分性的证明是显然的.

[参考文献]

[1]ARONSZAJN N.Theory of reproducing kernels[J].Trans Amer Math Soc，1950，68： 337-404.

[2]RICHTER S.Invariant subspaces in Banach spaces of analytic functions[J].Trans Amer Math Soc，1987，304： 585-616.

[4]MONTES-RODRIGUEZ A.Weighed composition operators on weighted Banach spaces of analytic functions[J].J London Math Soc，2000，61：872-884.

[6]OHNO S，STROETHOFF K，ZHAO R.Weighted composition operators between Bloch-type spaces[J].Rocky Mountain J Math，2003，33:191-215.

[7]WOLF E.Weighted composition operators between weighted Bloch type spaces[J].Bull Soc Roy Sci Liège，2011，80：806-816.

[8]冯丽霞.Dirichlet空间上Toeplitz算子的乘积[J].东北师大学报(自然科学版)，2015，47(4)：42-45.

[9]洪勇.含零阶齐次核的Hilbert型奇异重积分算子的有界性及范数[J].东北师大学报(自然科学版)，2014，46(1)：48-54.

(责任编辑：李亚军)

Finite rank weighted composition operators on analytic function space

ZHAO Lian-kuo

(School of Mathematics and Computer Science，Shanxi Normal University，Linfen 041004，China)

Abstract:A unified characterization of finite rank weighted composition operators on reproducing kernel Banach space of analytic functions is given.The main result shows that a weighted composition operator on reproducing kernel Banach space of analytic functions is finite rank if and only if it is a zero operator or a rank-one operator.

Keywords:analytic function space；weighted composition operator；finite rank

[文章编号]1000-1832(2016)02-0155-02

[收稿日期]2015-10-29

[基金项目]国家自然科学基金资助项目(11201274，11471189).

[作者简介]赵连阔(1979—)，博士，副教授，主要从事函数空间上的算子理论研究.

[中图分类号]O 177.1[学科代码]110·57

[文献标志码]A

[DOI]10.16163/j.cnki.22-1123/n.2016.02.031