基于评分合理因子的协同过滤推荐算法研究

张　震，华　钢

1.中国矿业大学信电学院，江苏徐州，221008；2.淮北师范大学计算机科学与技术学院，安徽淮北，235000

基于评分合理因子的协同过滤推荐算法研究

张震1，2，华钢1

1.中国矿业大学信电学院，江苏徐州，221008；2.淮北师范大学计算机科学与技术学院，安徽淮北，235000

摘要：研究了协同过滤推荐算法中评分矩阵的稀疏性特征，调查并分析了用户评分尺度的差异问题。为了提高过滤推荐算法的推荐精度，采用评分合理因子进行算法的改进，构建基于评分合理因子的协同过滤推荐模型及改进的协同过滤推荐算法RFCF。实验证明，清洗掉评分不合理的用户不能提高预测准确性，反而会使准确性大大降低；而采用评分合理因子修正相似度计算的准确性，可以明显提高预测精度和执行效率，并且在评价矩阵稀疏情况较严重的情况下也能够收到较好的效果。

关键词：评分合理因子；相似度度量；评分预测；协同过滤推荐

随着电子商务、社交网络、慕课、P2P应用和云计算等技术迅速普及，互联网信息资源的规模迅速扩大，在海量的信息中，人们要准确有效地甄选自己所需要的信息越来越困难。个性化推荐系统就是解决这一问题的有效方法之一。协同过滤推荐是现行推荐系统中应用最广泛的技术之一。协同过滤分析用户兴趣，在用户群中找到与指定用户具有相似兴趣的用户集，根据用户集中的这些相似用户的观点推导出对目标用户的推荐列表，形成推荐系统对用户喜好程度的预测[1-2]。协同过滤推荐基于这样一个假设：如果用户对一些项目的评分比较相似，说明他们具有相似的喜好，则他们对其他项目的评分也比较相似。因此，协同过滤推荐算法的依据是用户的评分。但随着用户规模与项目规模的逐渐扩大，数据的稀疏度呈指数增长，同时用户评分尺度的差异也是影响推荐精度的主要原因之一。目前，国内外学者针对稀疏问题与评分尺度差异问题进行了一系列研究，提出了一些解决方法。针对稀疏问题一般采用矩阵填充技术。最简单的填充办法是固定值填充或平均值填充，但这两种办法并不能从根本上解决稀疏性问题。预测填充技术[3-6]是目前研究最多的技术。降维[7-10]的方法也可以解决矩阵的稀疏性问题，但矩阵分解的开销太大，并且会导致信息的丢失。针对用户评分尺度差异的问题，J.Herlocker等人提出了一种基于皮尔逊相关系数的最大值改进[11-12]与最小值改进[13]，考虑了用户间共同评价项目的数目对相似度计算结果的影响。H.J.Ahn提出了从近邻度、影响力和流行度三方面改进相似性度量的方法[14]。曾建新等人提出了一种基于改进信息熵的协同过滤算法，考虑了用户间的交集大小及评分差异[15]。本文提出一种基于用户评分合理因子的相似度度量方法(简称为RFCF)，通过分析用户评分尺度的特点和用户评分对推荐结果的贡献差异，构建用户评价合理因子，改进相似度度量，消除评分尺度差异带给推荐算法的影响。

1问题的提出

准确查询目标用户的最近邻用户集是整个协同过滤推荐成功的关键。在协同过滤推荐算法中，用户对项目的评分是计算用户相似度和确定最邻近用户集的主要依据，其中评分矩阵的稀疏性和用户评分特点的差异是影响相似度计算的重要原因。

例如，在MovieLens数据集中，用户的评分特点是不同的，如有的用户对影片评分的高低反映在分值上的差距较大，而有些用户在分值上的差距较小。如图1所示。

图1分别给出了用户1、用户2和用户3对项目集的评分情况分布图，用户1与用户3的评分范围在[1,5]区间，而用户2的评分范围在[3,5]区间；同样是得分为3的项目，对于用户1与用户3是评价中等的项目，而对于用户2是评价极差的项目。因此，不同用户的评价尺度存在较大差别，这种差别对计算用户相似度影响较大，从而最终影响推荐算法的性能。

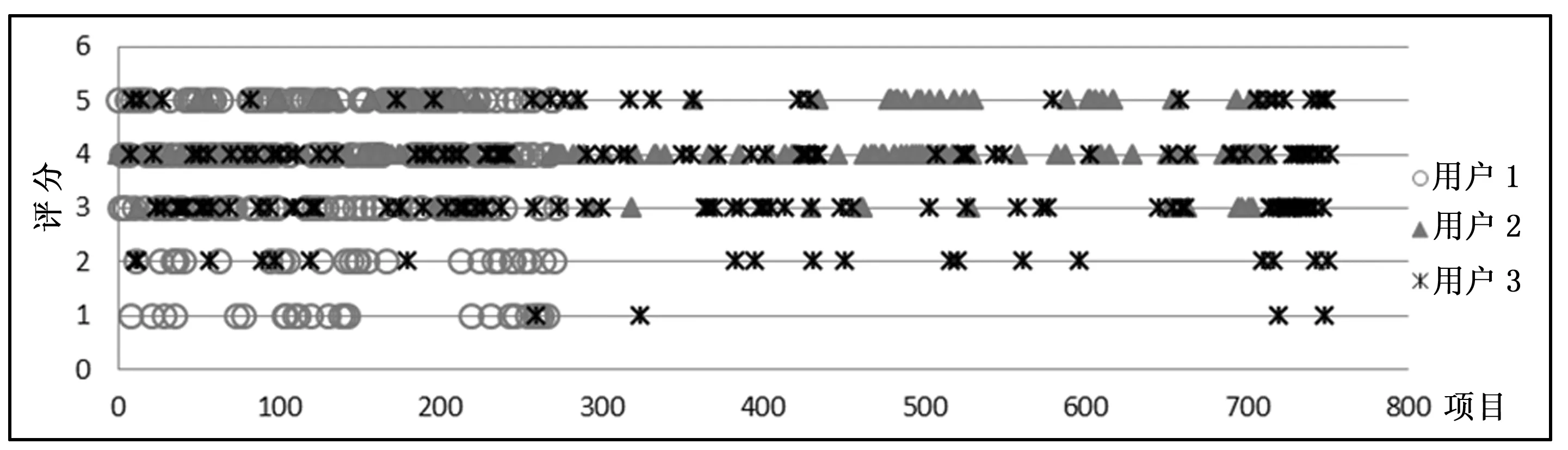
图1　评分情况分布图

2理论基础

定义1(用户-项目评分矩阵)：R={ru,j}，R表示移动用户对项目的评分矩阵，rk,j表示移动用户k对项目j的评分，评分值通常为[1,5]区间的整数。

定义2(项目集合):J={j|j∈L}，J表示项目集合，其中，L为项目ID集合。

定义3(用户集合):U={k|k∈M}，U表示用户集合，其中，M表示用户的ID集合。

定义4(用户评分合理因子):

(1)

利用(1)式计算上面三个用户的评分合理因子如表1所示。

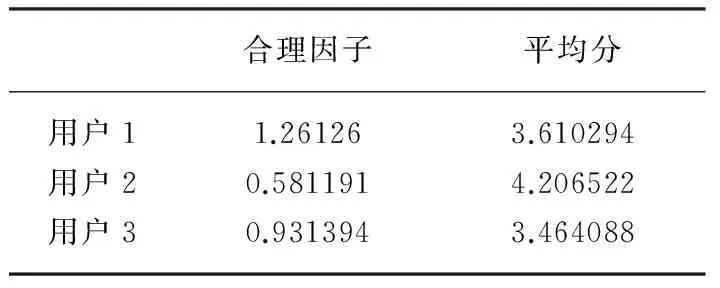
表1　用户评分合理性比较

表1显示，用户2的评分合理因子较小，平均分较高，说明该用户的评分普遍较高，必定影响相似度计算的准确性。

定义5(用户评分合理性向量)：δ={δk,k∈M}，δ表示用户评分合理性度量，其中，M表示用户的ID集合。

定义6(皮尔逊相关)：在评分系统中，不同用户给出的评分偏向是不同的，有的用户评分普遍偏高，而有的用户评分普遍偏低。皮尔逊相关通过减去用户的平均评分在一定程度上解决了评分偏向的问题。

(2)

定义7(改进的用户相似度矩阵)：SU={sim′(uk,uz) |uk，uz∈U}，SU表示用户之间的相似度矩阵，sim′(uk,uz)表示用户k与用户z的相似度，值越大，表示用户间的相似度就越高。

sim′(uk,uz)=

(3)

定义8(评分预测函数):预测用户k对商品j的评价函数，Pk,i代表用户k对商品j的预测评价。

(4)

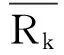
3改进的推荐算法

改进的协同过滤推荐模型包括数据预处理、基于相似度的最近邻用户集的选取、构建推荐引擎、得到推荐列表、模型评估(若满意，则输出TopN，否则，返回到数据预处理阶段重新进行挖掘)。

RFCF算法流程：

步骤1利用(1)式计算用户评分合理因子δk,k∈M，从而得到用户评分合理性向量δ。

步骤2设置δk的下限，并进行数据清洗，调整δk的取值，利用基于用户Pearson相似度的协同过滤推荐算法UPCF实验，验证利用评分合理因子进行数据清洗的有效性。

步骤3利用δk修正相似度度量，利用(2)式计算用户相似度sim′(uk,uz)，从而得到改进的用户相似度矩阵SU。

步骤4确定相邻用户集H的规模。

步骤5利用(3)式进行评分预测，求解P(k,j)的值，并根据P(k,j)的值，确定TopN。

步骤6采用平均绝对误差MAE与RMSE进行模型评估。

(5)

平均绝对误差是推荐系统中应用最广泛的评估方法，它通过计算预测评分与真实评价数据上的差别来衡量推荐结果的准确性。MAE的值越小，推荐精度就越高。

(6)

均方根误差反映了评分数据的离散程度，数值越小，说明离散程度越小，评分越趋于平均值。

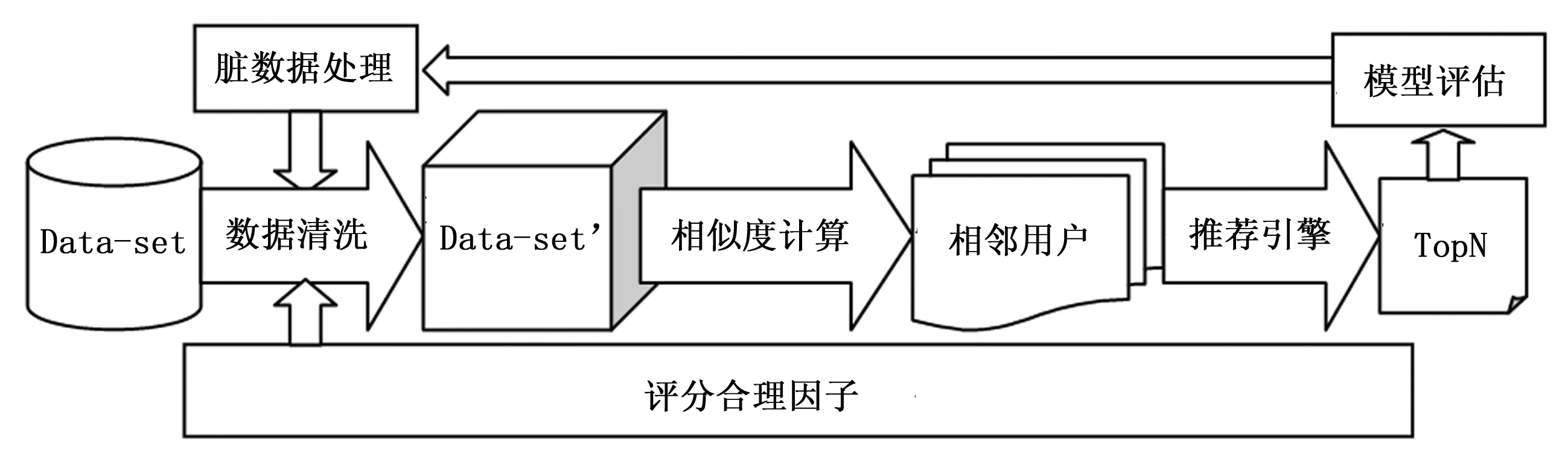
图2　改进的推荐算法模型

4实验分析

实验数据来自Minnesota大学GroupLensResearch项目组收集的MovieLens数据集，数据量共计10万条，包含了943位用户对1682部电影的评分。该数据集的稀疏程度高达93.7%。在该数据集中，选取80%作为训练集，20%作为测试集。

利用(1)式求每位用户的评分合理因子，通过删除ξi取值小于0.6的用户评分进行数据清洗，图3为基于用户Pearson相似度的协同过滤推荐算法UPCF在数据清洗前后的MAE与RMSE的变化。

图3显示，清洗前后预测的准确性发生明显的变化，清洗掉评分不合理的用户不能提高预测的准确性，反而会使准确性大大降低，说明简单地删除评分合理因子较小的用户是不可行的，不仅不能提高算法的精度，反而会加重矩阵的稀疏性。

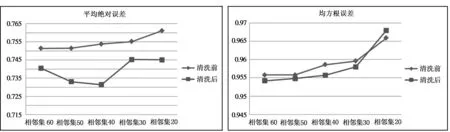
图3　清洗前后平均绝对误差与均方根误差的变化

为了进一步验证RFCF算法的有效性，突出算法的优势，从该数据集中首先随机抽取4万条评价，同样涉及943个用户对1682部电影的评分。该数据集的稀疏程度高达97.5%。在该数据集中，选取80%作为训练集，20%作为测试集。比较基于用户Pearson相似度的协同过滤推荐算法UPCF与基于用户评分合理因子的协同过滤推荐算法RFCF的MAE与RMSE，测试结果如图4所示。

图4　算法比较

从图4中可以看出RFCF算法和UPCF算法在MAE与RMSE上的对比情况，实验结果表明，RFCF算法能够有效地提高预测的准确性，且离散程度较小。同时，当稀疏度较大时，RFCF算法相对于UPCF算法的精度提高幅度较大，这说明RFCF算法在稀疏情况较严重的情况下也能够体现出较强的优势。

5结束语

本文介绍了一种基于用户评分合理性探究的协同过滤推荐算法RFCF。该算法从介绍用户评分特点入手，分析了用户评分尺度的差异，然后从数据清洗与改进相似度两个角度进行实验，验证了利用评分合理因子改进相似度方法的有效性。实验证明，RFCF算法比传统的推荐算法有明显的改进，并且在稀疏程度较大的情况下也可以有效地提高算法的精度。

参考文献：

[1]Nguyen T T,Kluver.Rating support interfaces to improve user experience and recommender accuracy[C]//Hongkong:In Proceedings of the 7th ACM Conference on Recommender Systems,2013:149-156

[2]Sarwar B,Karypis G,Konstan J,et al.Application of Dimensionality Reduction in Recommender System-A Case Study[EB/OL].[2016-01-18].http://www.docin.com/p-1035255326.html

[3]Cacheda F,Carneiro V,Fernandez D,et al.Comparison of collaborative filtering algorithms:limitations of current techniques and proposals for scalable,High-Performance recommender systems[J].ACM Transactions on the Web,2011,5(1):1-33

[4]Jung K Y,Hwang H J,KANG U-g.Constructing full matrix through naive bayes for collaborative filtering[C]//Kunming:PROCEEDINGS,2006:1210-1215

[5]Konstan J,Miller B,Maltz D.GroupLens:applying collaborative filtering to Usenet news[J].Communications of the ACM,1997,40(3):77-87

[6]Robles V,Larranaga P,Menasalvas E,et al.Improvement of naive bayes collaborative filtering using interval estimation[C]//Washington DC:Proceedings of the IEEE/WIC International Conference on Web Intelligence,2003:168-174

[7]Sarwar B M.Application of dimensionality reduction in recommender system-a case study[C]//New York:acm webkdd 2000 web mining for e-commerce workshop:acm press,2000:82-90

[8]Pariser A R,Miranker W.Dimensionality reduction via Self-Organizing feature Maps for collaborative filtering[C]//Orlando:Proceedings of International Joint Conference on Neural Networks,2007:1941-1946

[9]Abhinandan D,Mayur D,Ashutosh G,et al.Google News Personali zation:Scalable Online Collaborative Filtering[C]//New York:Proceeding of the 16th international conference on World Wide Web,2007:271-280

[10]Vozalis M G,Margaritis K G.Applying SVD on item-based filtering[C]//Wroclaw Poland:Proceedings of the 5th International Conference on Intelligent System Design and Applications,2005:464-469

[11]Herlocker J L,Konstan J A,Borchers A.An Algorithmic Framework for Performing Collaborative Filtering[C]//Berkeley:Proceedings of the 22nd Annual Interational ACM SIGIR onference on Research and Development in Information Retrieval(SIGIR’99),1999:230-237

[12]Herlocker J L,Konstan J A,Terveen K,et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems,2004,22(1):5-53

[13]HAO M,Irwin K,Michael R L.Effective missing data prediction for collaborative filtering[C]//Amsterdam:Proceedings of the 30th annual international ACM SIGIR conference on Research and development in information retrieval,2007:23-27

[14]Ahn H J.A new similarity measure for collaborative filtering to alleviate the new user cold-starting problem[J].Information Sciences,2008,178(1):37-51

[15]曾建新，杨宁，夏培勇．一种基于改进信息熵的协同过滤算法[J]．微计算机信息，2012，28(8)：181-183

(责任编辑：汪材印)

doi:10.3969/j.issn.1673-2006.2016.05.026

收稿日期：2016-02-25

基金项目：淮北师范大学校级教研项目“翻转课堂在高校教学中的应用研究”(jy14138)。

作者简介：张震(1977-)，女，安徽淮北人，在读博士研究生，副教授，主要研究方向：智能信息处理。

中图分类号：TP391

文献标识码：A

文章编号：1673-2006(2016)05-0096-04