信息不完备情况下多因素工序质量诊断方法
2016-06-28李金艳余忠华徐宣国
李金艳, 余忠华, 徐宣国
(1.浙江大学 机械工程学院, 杭州 310027; 2.江苏科技大学 经济与管理学院, 江苏 镇江 212003)
信息不完备情况下多因素工序质量诊断方法
李金艳1,2, 余忠华1, 徐宣国2
(1.浙江大学 机械工程学院, 杭州 310027; 2.江苏科技大学 经济与管理学院, 江苏 镇江 212003)
摘要:为解决信息不完备情况下的多因素工序质量诊断问题,在工艺机理分析的基础上,提出基于贝叶斯网络模型构建与推理的问题溯源方法. 在贝叶斯网络结构学习过程中,利用基于评分/搜索的思想对基于工艺的预先假设结构,通过互信息参量排序降低学习复杂度. 针对生产过程中随机因素对诊断准确性的影响问题,结合Leaky Noisy-OR模型引入随机参量节点,对数据需求和推理进行降解优化. 以沟道磨削表面形貌质量问题的诊断为例,给出模型构建与推理程序,并验证了所构建模型及优化方法的可行性和有效性.
关键词:工序质量问题;贝叶斯网络; 互信息;Leaky Noisy-OR模型;沟道磨削
产品的质量是关系到企业市场竞争能力的重要指标. 随着市场竞争的日益加剧,生产模式向多品种小批量方面发展. 由于加工工艺的复杂性、监测方法的局限性以及信息的不完备,导致工序质量问题的诊断成为影响生产的瓶颈. 针对该问题国内外学者进行了大量研究,主要集中在物理解析建模和数据驱动建模两个方面. 物理解析建模[1]是在专业技术经验和工程知识的基础上对制造过程进行分析[2],识别关键控制特征和关键产品特征之间的关系[3]. 数据驱动建模方法则是基于过程测量数据[4],利用多元统计分析提取数据特征的方式识别质量问题[5]. 两者在应用方面取得了瞩目成果,但均建立在工艺知识和检测数据信息完备的前提条件下. 在部分实际生产过程中,由于工艺、设施、环境等对质量问题影响机理的模糊性和监测条件的限制,无法获取足够的信息建立精确的解析模型或借助统计方法进行问题诊断.
贝叶斯网络是一种可以进行不确定知识表达和推理的方法,利用其对不确定性的推理能力,可以有效地进行多源信息表达与融合,适用于多源异类、不确定信息条件下的知识表达和推理. 目前,该方法的应用研究主要集中于可靠性、风险分析以及系统故障诊断等领域[6]. 在制造过程工序质量诊断方面,文献[7]结合该方法针对汽轮机转子法兰联接孔的加工缺陷进行了建模和推理研究,文献[8]利用该方法建立了柔性生产线质量诊断模型,这些研究均建立在因果关系明确且结构简单的前提下;文献[9]针对小数据集情况通过网络结构学习和参数学习,对某车型侧围装配过程进行了贝叶斯网络建模与偏差源诊断,但未考虑诊断过程中随机因素的影响.
本文在上述研究的基础上,以贝叶斯网络为建模工具,首先结合工艺知识对相关影响因素和质量问题进行预先因果假设,建立初始网络结构;然后,分别利用基于评分/搜索方法和Leaky Noisy-OR模型进行网络结构学习和条件概率推理的降解优化;最后,以沟道磨削表面质量问题诊断为例,对所构建模型及优化方法的可行性和有效性加以验证.
1贝叶斯网络基本原理
1.1概念界定
贝叶斯网络[10]是一种以网络结构表示变量间依赖关系的概率图模型. 在贝叶斯网络[11]中,定性信息主要通过网络的拓扑结构表达,定量信息则通过节点的先验概率和条件概率表示,即B=
定义1条件独立假设. 给定节点vi,其父节点f(vi)状态给定后,vi条件独立于非vi子代节点构成的任何节点集. 即若
则
定义2条件概率与链乘原则. 由v1,v2∈V,P(v2)>0,知
链式规则:V={ v1,v2,…,vn},其联合概率可表示为
2基于工艺-工况状态-问题的贝叶斯诊断网络模型构建
产品一般由多个零部件组成,每个零件又由多道工序加工完成. 为了保证产品的最终加工质量,需要对每个零件的加工质量进行控制,而零件的加工质量又取决于其加工工序序列的稳定性.
在生产工艺机理明确,检测数据信息完备且样本量足够的情况下,加工工序质量可利用领域知识结合数学模型表达如下[1]:
yk=Ckxk+vk.
式中:xk为质量特征向量, yk为xk的测量表征向量, xk-1为与其存在影响关系的前接工序质量特征向量, uk为本工序加工状态向量, Ak-1、Bk、Ck为由领域知识决定的结构矩阵,wk、vk为随机变量.
在实际生产过程中,由于工序质量问题(yk)发生的随机性、工艺的复杂性(Ak-1、Bk、Ck)以及诊断信息(xk-1, uk)的不完备性,致使无法搜集到足够的信息建立结构模型. 为此,需要由专家或技术人员通过对工况情景和相关参量的调查,利用经验对搜集的质量问题证据进行分析找出根源,这个过程带有“试错”的理念,并缺乏系统性. 多因素工序诊断过程本质上就是从问题现象到影响因素的推理过程[7]. 本文从系统论的角度对质量问题进行建模,将质量问题的发生看作是具体加工单元中各种要素节点相互联系作用形成的结果[12],采用适用于不确定性问题表示与推理的贝叶斯网络作为建模工具,影响因素与质量特性指标间的因果关系及影响程度分别通过贝叶斯网络模型的有向无环图和条件概率表进行定性的表达和定量的评估, 概念模型如图1可知:若将先验知识与现有信息融合通过贝叶斯网络可以溯源质量问题影响因素的发生情况. 此时,B=
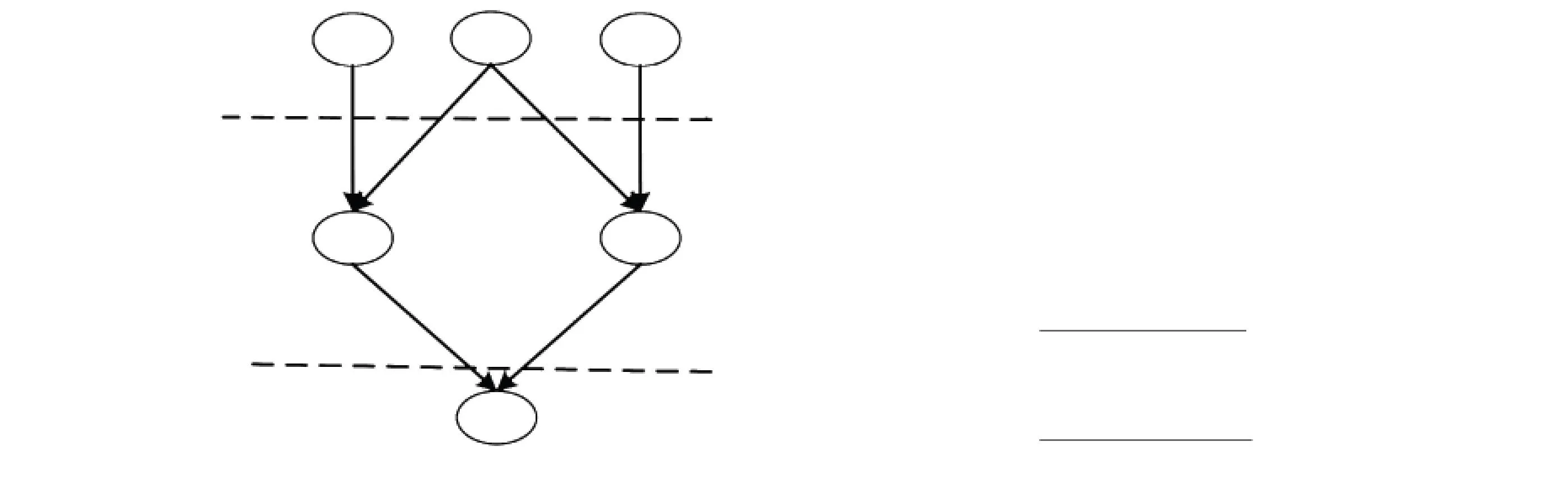
图1 质量问题诊断的贝叶斯网络因果机制示意
由图2(a)所示,若将节点集S′={xk-1,uk,wk}视为一个整体,则转化为如图2(b)所示,此时节点xk只有一个父节点S′和一个子节点yk,同时xk的存在,不影响S′→yk的概率传播,因此根据文献[13],可以将节点xk删除,直接构建S′→yk的有向边,见图2(c),此时S={S′,ck,vk}={xk-1,uk,wk,ck,vk},O={yk},其中ck为测量相关影响因素,其他节点含义与上同.

(a)初始结构 (b)简化结构 (c)优化后的结构
各变量的联合概率分布P为

由于工艺复杂性及相关信息的模糊与不完备性,所构建的贝叶斯网络依然无法避免节点众多、结构模糊复杂对结构学习与条件概率推理造成的推演难度问题.
3贝叶斯网络结构学习与条件概率推理优化
3.1结构优化
对于单工序的质量问题诊断采用质朴型贝叶斯结构,设为两层,即影响因素层S={s1,s2,…,sn}和质量问题表征层O={o1,o2,…,om},所有节点为[0,1]二值状态,同时满足假设条件:1)输入层节点之间互为独立;2)在给定父节点情况下,条件独立于非子代节点构成的任何节点集;3)∀oj∈O,Nf(oj)≤α,其中α为某一限值. 结构学习主要是确定工序质量问题与相关影响因素之间的关联关系,目前主要有基于搜索与评分的方法和基于依赖关系分析的方法. 针对节点较多,信息量不足,需要较多借助历史统计信息与专家知识的情况,前者学习效率更高一些. 为此本文采用基于评分搜索的K2算法,针对一个给定的初始结构,利用互信息作为评分函数使其变量有序,逐步增加或删减有向边,从而确定出一个较好的网络结构.
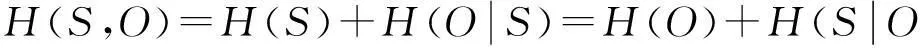
由量化表述信息X不确定度的信息熵:
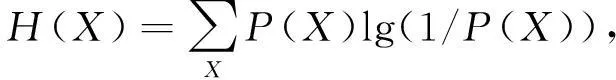
得
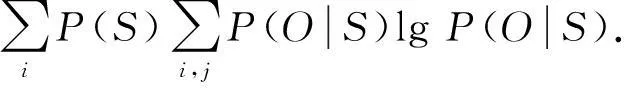
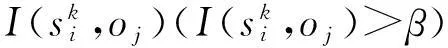
根据工艺领域知识对S与O的依赖关系进行预先假设,对I(S,O)表达的依赖或影响程度进行排序得出简约后的因果关联关系,结构复杂度降至m×α. 但对条件概率计算而言,若存在α个原因父节点,则需估计2α条概率,在样本数据并不充分的情况下,获得条件概率表中的每一项是很困难的. 此外,实际生产过程中由于wk、vk等随机因素以及I(si,oj)<β节点的存在,即使简约后的各si节点均处于控制稳态,O仍有可能发生异常.
3.2基于Leaky Noisy-OR的维数优化
Noisy-or gate模型是解决数据缺失问题的一种方法[14]. 在网络结构已知,具备一定的专家知识和经验的条件下,利用 Noisy - or gate模型可以近似确定相关节点的条件概率. Noisy-or gate模型成立的假设前提条件[15]除3.1节所提及1)、2)外,对于每一个父节点,设

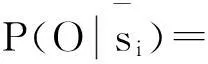
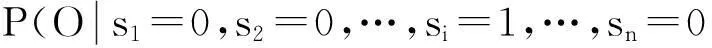
由p1,p2,…,pn可以确定问题节点O的条件概率表
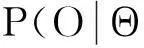
pL为其他节点正常时,随机参量L导致质量问题发生概率,即
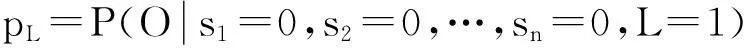
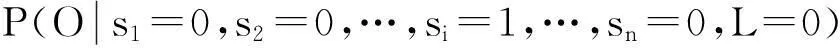
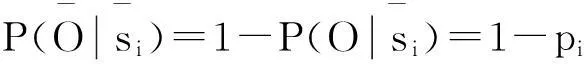
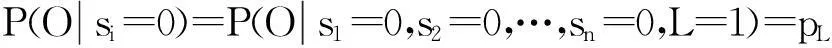
(1)
pi+pL-pi×pL.
从而得
pi=(P(O|si=1)-pL)/(1-pL) =
(P(O|si=1)-P(O|si=0)/
(1-P(O|si=0)).
(2)
质量问题发生以及各原因节点异常的概率为
(3)
(4)
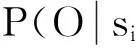
4应用
在轴承的应用过程中,套圈沟道[16]负责引导滚动体沿着轨道作轨迹运动,需要承受较大的轴向和径向负载,是影响轴承寿命的主要环节. 目前,沟道大多采用变进给切入磨削方式,其原理是利用经圆弧砂轮修整器修整过的成形砂轮,做垂直于套圈沟道表面的切入进给,通过工件和砂轮的相对运动生成圆弧沟道. 该过程主要分为快速趋近、粗进给、细进给和光整4个阶段,加工精度直接影响到轴承使用时的振动和噪声,其中对精度影响最大的是沟道表面形貌问题,主要呈现方式有圆度误差、表面粗糙度和波纹度误差.
本文以608-2RS深沟球轴承的沟道磨削工序表面质量问题诊断为例论证上述建模、优化和推理过程的可行性.
4.1基本工艺
由于608-2RS深沟球轴承属于精密轴承范畴,以内圈外径做工艺基准,采用浮动支撑方式. 该工序基本工艺信息如下:
采用608-2RS球轴承沟道磨削. 材料为GCrl5轴承钢,硬度为60~65 HRC. 加工设备采用3MZl43A/1型自动球轴承外圈沟道磨床,加工精度为E-D级. 砂轮尺寸规格18 mm*3.5 mm*4 mm,粒度100~125 μm,磨料为MA,陶瓷结合剂,硬度L.磨削液为5#机油. 砂轮转速为48 000 r/min,工件转速960 r/min.
沟道表面形貌主要涉及沟道粗磨和精磨两个工序,影响磨削轴承沟道圆度的主要因素可归纳为前接工艺特征、物理加工环境、工艺系统状态、执行工况以及测量等方面,具体如图3所示.
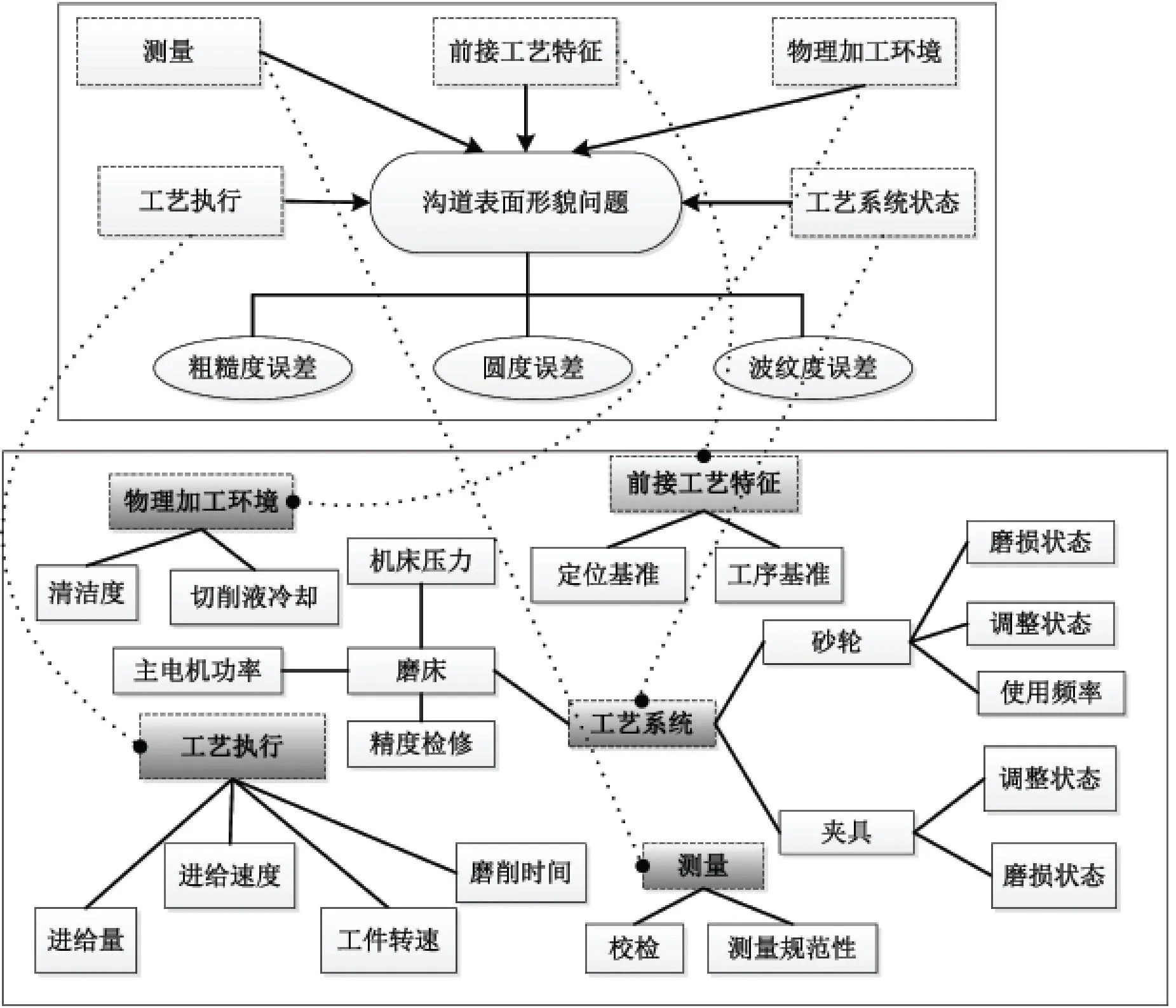
图3 沟道表面形貌问题相关影响因素的工艺分析
4.2沟道表面形貌问题诊断
针对沟道表面形貌问题(O),在以上工艺分析的基础上,利用鱼骨图结合头脑风暴,进行相关影响因素节点的归纳,做出对贝叶斯网络结构的初步假设. 以某时段圆度超差问题O2为例,具体的质量问题诊断步骤如下:
Step 1确定网络节点集V={S,O},如表1所示,各节点状态为二值变量:正常状态(0)、异常状态(1).
Step 2基于领域知识对S,O的依赖关系进行预先假设,如图4所示.
Step 3计算圆度误差问题节点O2与各影响因素节点之间的互信息I(si,o2),确定简约后的圆度误差问题O2的贝叶斯网络拓扑结构,结果如图5所示.
Step 4设节点参量L表示磨削过程与测量过程的随机影响因素,结合Leaky Noisy-OR Gate模型求解圆度误差O2的相关影响因素条件概率.
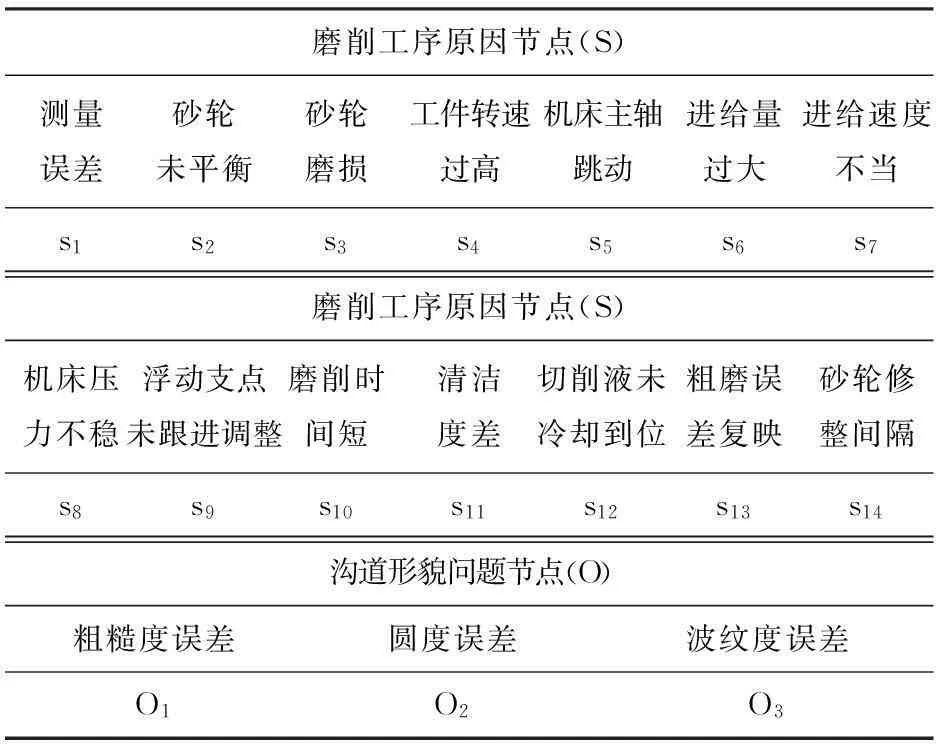
表1 诊断模型节点

图4基于领域知识的沟道表面形貌问题的预设网络拓扑结构
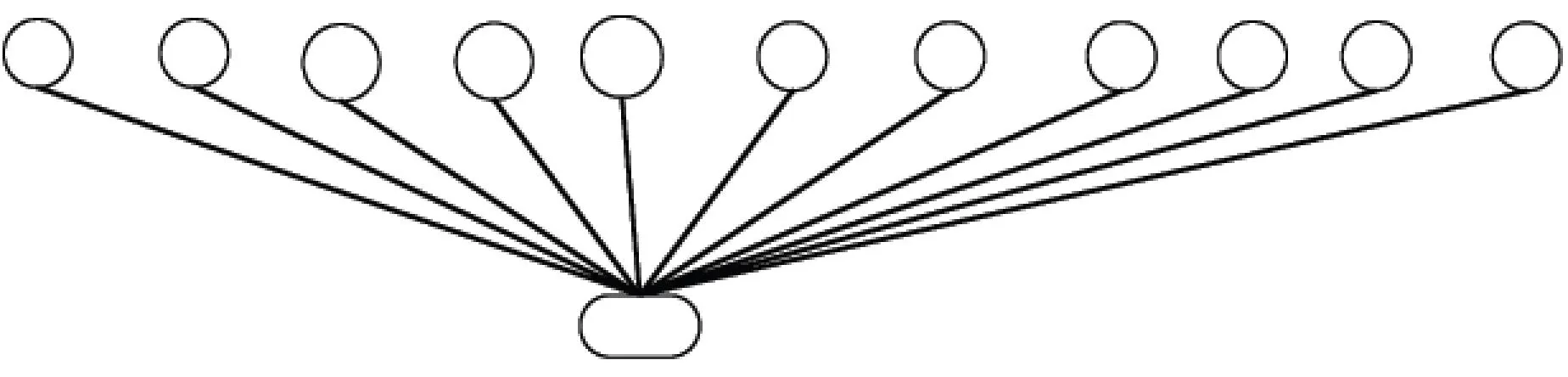
图5 轴承沟道圆度超差问题诊断贝叶斯网络拓扑结构
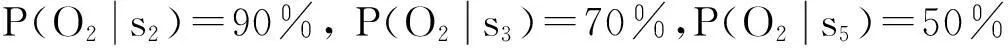
Step 5将各影响因素节点条件概率从大到小排序,初步取阈值γ≥50%作为影响因素的判定界值,结果如表2所示.

表2 主要因素诊断结果
根据表2结果,由操作人员对执行工况逐一调整排解.
Step 6如果经检测,圆度误差问题O2依然存在,则将所得检测和工况信息作为新的证据并入,转至Step 1继续,直至问题解决.
4.3问题诊断结果讨论
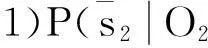
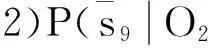


5结论
1) 本文在工艺机理分析的基础上,针对数据信息缺失情况下的工序质量诊断问题,采用基于评分搜索的K2算法构建简约贝叶斯网络模型;
2)结合Leaky Noisy-OR节点模型,将生产过程中随机因素的影响纳入到推理模型,使概率推理更加接近实际的同时,简化了估计条件概率量;
3) 利用沟道磨削表面形貌质量问题诊断对所构建模型及优化方法的可行性和有效性进行了验证,并针对数据缺失情况与质朴贝叶斯网络做了比较评估;
4)由于不同时刻、不同工况下各节点的先验概率为动态参量,而本文是从静态的角度切入进行的研究,所以在推广应用中尚有一定的局限性,需要进一步深入分析动态贝叶斯网络在这方面的拓展.
参考文献
[1] SHI J J,ZHOU S Y.Quality control and improvement for multistage systems: A survey[J].IIE Transactions,2009 (41):744-753.
[2] 张磊,张志胜,周一帆,等.基于半参数回归模型的制造过程加工误差流建模与分析[J].机械工程学报,2013,49(15):180-185.
[3] HAN K, WANG K B. Coordination and control of batch-based multistage processes[J].Journal of Manufacturing Systems,2013 (32): 372-381.
[4] 牛青,莫蓉,万能.基于二分法的多因素工序质量诊断算法[J].机械工程学报,2014,50(2):202-206.
[5] 王宁,徐济超,杨剑锋.多级制造过程关键质量特性识别方法[J].计算机集成制造系统,2013,19(4):888-895.
[6] WEBER P,MEDINA-O G, SIMON C, et al. Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas[J]. Engineering Applications of Artificial Intelligence,2012,25(4):671-682.[7] 李丽娟,高建民,陈琨.基于Bayesian网络的机械加工缺陷溯源方法[J].计算机集成制造系统,2010,16(7):1452-1457.
[8] 马淑梅,黄庆,谢楠.基于贝叶斯网络的柔性生产线质量诊断模型[J].机械设计与研究,2012,28(6):107-110.
[9] 刘银华,金隼.基于小数据集贝叶斯网络建模的偏差源诊断方法[J].上海交通大学学报,2012,46(5):701-705.[10]PEARL J.Probabilistic reasoning in intelligent systems: networks of plausible inference [M].San Mateo,CA: Morgan Kaufmann,1988.
[11]张连文,郭海鹏.贝叶斯引论[M].北京:科学出版社,2006.
[12]YANG L, LEE J.Bayesian belief network-based approach for diagnostics and prognostics of semiconductor manufacturing systems[J].Robotics and Computer-Integrated Manufacturing, 2012,28(1): 66-74.
[13]董晔弘,向东,龙旦风,等.基于贝叶斯网的制造工艺质量建模方法[J].计算机集成制造系统,2010,16 (12):2564-2569.
[14]ONISKO A,DRUZDZEL M J,WAYSYLUK H.Learning Bayesian network parameters from small data sets: application of Noisy-OR Gates [J].International Journal of Approximate Reasoning,2001,27(2):165-182.
[15]王华伟,周经伦,何祖玉,等.基于贝叶斯网络的复杂系统故障诊断[J].计算机集成制造系统,2004,10(2):230-234.[16]周福章,夏新涛,周近民.滚动轴承制造工艺学[M].西安:西北工业大学出版社,1993.
[17]严思晗.轴承套圈沟道磨削的进给状态参数监测及其工艺试验研究[D].杭州:浙江大学,2006.
(编辑杨波)
Diagnosis method of multi-cause process quality under incomplete information
LI Jinyan1,2, YU Zhonghua1, XU Xuanguo2
(1.School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China;2. School of Economics and Management, Jiangsu University of Science and Technology, Zhenjiang 212003, Jiangsu, China)
Abstract:Aiming at the problem of multi-cause process quality diagnosis under the circumstance of information losing, a method based on construction and inference of Bayesian network model is proposed. In the learning process of Bayesian network structure, the thought of score/search is adopted for the assumption structure so as to reduce the learning complexity through the mutual information parameters sorting. In view of the influence of random factors on the diagnostic accuracy, the Leaky Noisy-OR model is adopted, which simultaneously degrades the requirement quantities of data and reasoning. In the end, a problem diagnosis for channel grinding is taken as an example to verify the feasibility and effectiveness of the proposed model and optimization method.
Keywords:process quality issues; bayesian networks; mutual information; Leaky Noisy-OR model;channel grinding
doi:10.11918/j.issn.0367-6234.2016.07.014
收稿日期:2015-10-29
基金项目:国家自然科学基金 (71371088)
作者简介:李金艳(1982—),女,博士研究生; 余忠华(1963—),男,教授,博士生导师
通信作者:余忠华, caq_221@zju.edu.cn
中图分类号:TP202
文献标志码:A
文章编号:0367-6234(2016)07-0088-06
