基于节约里程法的同城配送路线规划

杨秋

中图分类号：F252 文献标识码：A

内容摘要：本文考虑将节约里程法运用到同城配送中，并以销售汽车及其零部件通过运输车从配送中心运往4S店的路线规划为研究对象，综合考虑里程、时间、成本、服务等多方面因素，以期实现汽车的JIT配送。

关键词：节约里程法 同城配送 路线规则

相关理论基础

（一）同城配送

同城配送是从区域配送中发展而来的，它将不同品牌、不同种类、不同供应商的货品组织起来，通过物流信息化平台，在货物的仓储、加工等物流活动的过程中，实时监控，以实现同一城市资源的统一调配，高效率地将货物送到顾客手中，是一种精确到时间、地点的自动化配送系统。

目前，同城配送作为物流配送体系的最后一环已经引起了越来越多学者的关注。董媛（2008）根据我国国情，分析我国同城配送物流的现状及存在的问题，并提出了改进建议；杨春燕（2014）从物流人才的角度，分析了同城配送物流人才培养现状，并提出了关于同城配送物流人员的培养途径。已有学者从不同角度对同城配送物流进行了研究，然而考虑用节约里程法进行同城配送物流路线规划的研究却屈指可数，本文拟用该方法进行销售汽车的同城配送路线规划研究。

（二）节约里程法

节约里程法是用来解决运输车辆数目不确定问题的最有效的启发式算法。用于解决配送路线规划问题的基本思想是：假设P为配送中心，A和B分别是配送点，P与A之间的距离为a，P与B之间的距离为b，A与B之间的距离为c。如果用两辆车分别从P向A和B配送，车辆运输里程为2a+2b。如果只派一辆车，从P向A、B巡回配送，则车辆运输里程为a+b+c。两种配送方法车辆运输里程差为（2a+2b）-（a+b+c）=a+b-c。如果a+b-c>0，那么第二种方法下的车辆运输里程优于第一种配送方法下的车辆运输里程。如果多家配送，可以根据节约里程的大小顺序连接各配送点并规划出最佳路线。

该方法已在物流配送中得到了应用，张文华（2012）、李如姣（2008）运用该方法，根据具体的物流公司已有的配送中心和路线，对其进行了优化；张颖敏（2011）综合考虑车流量、客户分布状况及车辆载重情况，运用该方法对配送路线进行了优化，并提出了负载配送网络模型的改进建议。该方法在跨国跨省物流配送中已颇有成效，研究证明其在同城配送中也具有较高适用性。

节约里程法在同城配送中的应用

传统的节约里程法只是节约“里程”，但在实际运作过程中，节约了里程并不一定节约了成本，尤其是在城市内的配送过程中，最短的路程往往在时间、成本等方面不是最优的。因此，本文所指的节约不光是狭义的“里程”，而是综合考虑里程、时间、成本、服务等多方面因素。

本文将以国内某汽车销售公司的同城配送情况为例，说明节约里程法在同城配送过程中的应用。假定某汽车销售公司的某一区域配送中心P承担周边A、B、C、D、E、F、G、H、I九家4S店的配送任务，如图1所示。

（一）最优路线及其运输成本的计算

在每两点之间（包括配送中心和4S店）往往会有多条路线，首先要确定这些路线中的最优路线，运用公式（1）及公式（2）确定两点之间的最优路线及其运输成本。

Cn=Cn1+Cn2 （1）

Cn2=k（tn-smin/v0） （2）

其中，Cn表示通过第n条路线配送的运输成本；Cn1表示运输过程中的显性成本（包括燃油费、工资、车辆折旧、保险费等）；Cn2表示隐性成本（由配送延误等非正常事件引起的成本）；v0表示配送过程中车辆的正常运输速度；smin是指所有路线中最小里程的路线；tn是指第n条路线的运输时间；k为常数，其值取决于配送时效的重要性程度。

在两点之间的各条路线中，Cn值最小的路线就是最优路线，最小值Cn即其运输成本。

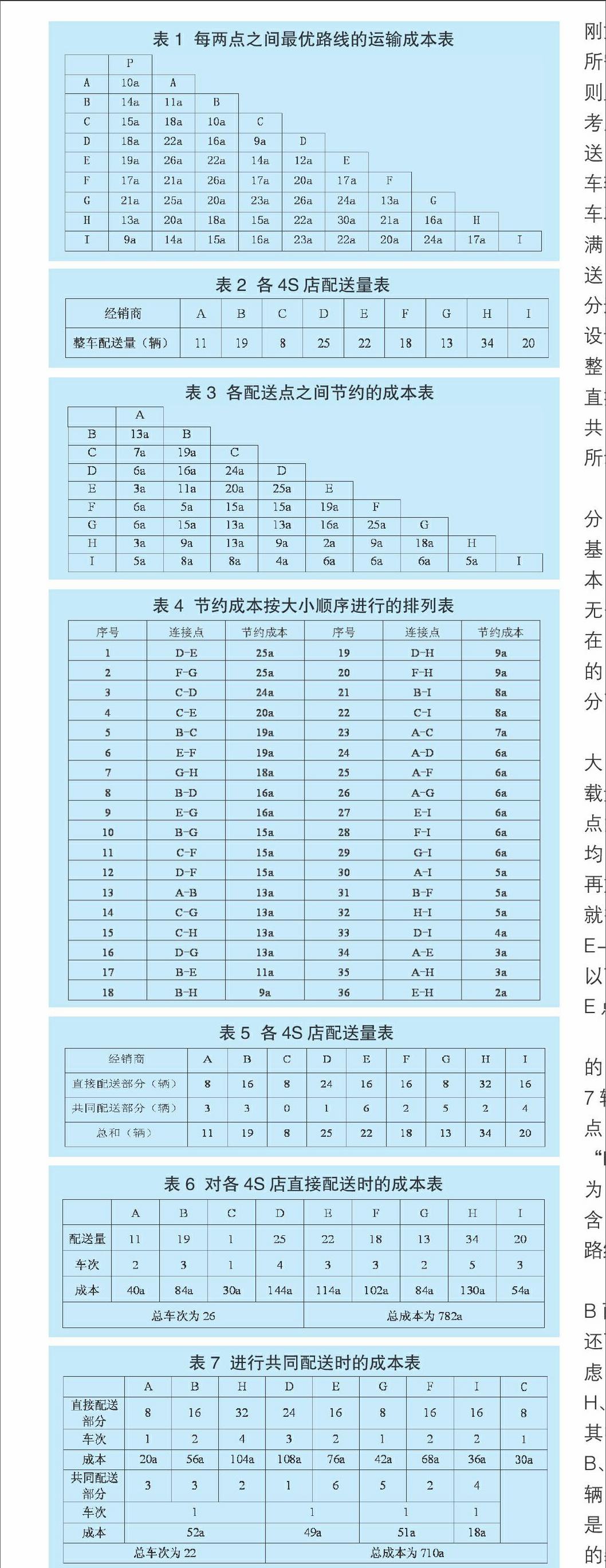
假定每两点之间最优路线的运输成本如表1所示，其中，a为常数，表示单位运输成本，单位为（元）。

（二）各经销商（4S店）配送量的确定

假定某一次对A、B、C、D、E、F、G、H、I九家4S店的配送任务只有整车配送，配送量如表2所示。

（三）可节约成本的计算

计算各配送点可节约的成本，计算结果如表3所示。

（四）成本节约排序

根据表3计算出的节约成本表，对已节约的成本按大小顺序进行排列，如表4所示。

（五）给货运车辆分配配送任务

对于一家4S店来说，如果其需求量刚好能满足车辆满载（即所需货运车车次为整数），则直接对其进行配送，不考虑与其他4S店共同配送；若其需求量不能满足车辆满载（即所需货运车车次不是整数），则对能满足满载的部分直接配送，对不能满足满载的部分进行共同配送。因为假设该公司的运输车能装载整车8辆，所以各4S店直接配送的任务量和需要共同配送的任务量如表5所示。

本文对共同配送部分的任务进行合理安排，基本思想是按照节约成本的大小顺序（不考虑无需共同配送的C点），在满足货运车辆装载量的前提下，给货运车辆分配任务，步骤如下：

首先，将节约成本最大的D、E连接起来，装载量为7辆，因为其他各点的共同配送部分装载量均超过1辆，所以不能再加入任何一个点。这样就得到一条路线“P-D-E-P”，装载量为7辆。以下便不再考虑含C、D、E点的路线了。

其次，节约成本最大的是F-G，装载量共为7辆，也不能再并入其他点，因此得到第二条路线“P-F-G-P”，装载量为7辆。以下便不再考虑含C、D、E、F、G点的路线。

再次是A-B路线，A、B两点的装载量共6辆，还可再连接一个点，则考虑与A或B点与剩余的H、I两点连接的节约成本，其中最大的是B-I，但A、B、I三点的装载量超过8辆，不满足条件，接下来是B-H，A、B、H三点的装载量为8辆，满足条件。这样得到第三条路线“P-A-B-H-P”，装载量为8辆。

最后只剩下I点，只能直接对其配送。得到第四条路线“P-I-P”，装载量为4辆。

因此得到的配送路线有4条，如图2所示。

计算方案在此假定的条件下所节约的成本。若对各4S店直接配送，成本如表6所示。

依照方案，将各4S店不能满载的部分进行共同配送。这样一来的总成本如表7所示。

从分析结果可以看到，用节约里程法的思想对不能满载的配送任务进行整合共同配送，无论从车次上看还是从成本上看，都能得到较好的优化。

结论

本文运用节约里程法对销售汽车的同城配送路线进行规划。通过案例分析可以看出，配送车次由原来的26辆次优化后只需22辆次，配送过程中的总成本由原来的782单位优化为710单位。不仅是运输过程中配送资源得到了优化，在总成本方面也得到了优化。

同城配送的发展能够促进城市的发展，同时，同城配送作为“最后一公里”，一直以来制约着物流效率的提升。本文综合考虑配送过程中的成本、时间及服务等因素，通过运用节约里程法对汽车及其零部件从配送中心运往4S店的运输路线规划研究发现，节约里程法可以有效解决城市“最后一公里”配送问题。本文研究结果可推广应用到其他商品货物的短距离配送，同时物流企业可以考虑开发配送管理系统，以便于简化使用难度，提高运用效率。

参考文献：

1.杨春艳.同城配送环境下物流人才的培养研究[J].山西经济管理干部学院学报，2014（4）

2.王文佳，侯典辉.绿色蔬菜同城配送的可行性分析[J].商业经济，2013（10）

3.董媛，刘影.我国物流同城配送问题及改进措施[J].中小企业管理与科技（上旬刊），2008（10）

4.张文华.基于节约里程法的物流配送路线优化[J].物流工程与管理，2012（3）

5.张颖敏.基于节约里程法的物流配送线路优化与改进研究[J].物流科技，2011（4）

6.李如姣.“节约里程法”在某物流公司配送中心的实际运用[J].科技资讯，2008（28）