脑卒中发病影响因素的统计分析

李　一

(成都工业学院　信息与计算科学系，成都　611730)

脑卒中发病影响因素的统计分析

李一*

(成都工业学院信息与计算科学系，成都611730)

摘要：依据2012年全国大学生数学建模竞赛C题数据，运用SPSS软件对患脑卒中人群分别从性别、年龄、职业、发病时间、诊断时间等进行频数统计和描述统计，分析脑卒中发病的规律和特征。在对气象资料和发病人数进行相关分析的基础上，剔除随机因素和季节变动对脑卒中发病的影响，建立多元线性回归模型，采用逐步回归方法求解以避免多重共线性，并对模型求解结果进行检验。结论：最高气温和平均相对湿度越低越易得脑卒中，最高气压越高越易得脑卒中。

关键词：脑卒中；统计描述；多元线性回归

“脑卒中”又称“中风”、“脑血管意外”，是一种急性脑血管疾病，具有较高的发病率、致残率和死亡率，是威胁人类生命的严重疾病之一，与环境因素(包括湿度和气温)之间存在密切关系。通过分析脑卒中发病的气象因素对疾病做定量分析和风险评估，有利于及时提醒易患人群采取针对性措施；有利于非易患人群评价自身患病风险，进行预防和保护；更有利于卫生部门和医疗机构合理调配医生、药品、床位等医疗资源。现有研究多通过扩大时距或计算差值等方式消除随机因素的影响，再通过人为筛选确定自变量，建立多元线性回归模型，如：王玉苏等[1]汇总各月气候因素，进行多元线性回归拟合；张远等[2]按月计算气候因素平均值及其高低差值，得出非线性回归方程；张明会[3]建立均值气候模型和差值气候模型多元线性回归模型，计算“发病因子”的估计值。本文通过指数平滑的方式消除随机因素和季节影响，采用逐步回归方法求解以避免多重共线性，在保留数据信息完整性的同时，较好地避免了人为筛选自变量的主观性。

1数据来源及处理

本文所用数据为“2012年高教社杯全国大学生数学建模竞赛”赛题C题“脑卒中发病环境因素分析及干预”所提供的中国某城市各家医院2007年1月至2010年12月的脑卒中发病病例信息以及其间当地的逐日气象资料。

为满足分析的需要和便于SPSS软件识别，本文先将所有数据的格式转换为统一格式，处理后的数据若出现空格、无数据，SPSS软件均默认为缺失值。

1.1日期数据的处理

1)将缺少发病日期的数据修正为空格；2)发病时间或诊断报告时间缺少具体日期的数据修正为空格；3)将诊断报告时间减去发病时间定义为延误治疗时间，时间间隔小于0的数据修正为空格；4)只考虑2007年1月到2010年12月的发病资料。

1.2年龄数据的处理

1)年龄大于120的数据视为缺失值；2)将年龄为“###”、“#REF！”、“6+1”均修正为空格；3)参照中国年龄分类法先将年龄分为5组，初步分析发现童年和少年患病人数较少，所以将其划分为同一组，即未成年(17岁以下)、青年(18～40岁)、中年(41～65岁)。考虑到老年期的发病率高，所以再将老年期细化分为初老期、中老期和年老期，即初老期(66～72岁)、中老期(73～84岁)、老年期(85岁以上)。

1.3职业数据的处理

将职业编号除1农民、2工人、3退休人员、4教师、5渔民、6医务人员、7职工、8离退人员外的数据均修正为空格。

1.4奇异值分析

对修匀后的气象资料和发病人数使用SPSS软件“探索分析”功能，查找奇异值，分析奇异值的数值特征，选择使用平均值替代奇异值。

2脑卒中发病影响因素的统计分析

2.1影响脑卒中发病的气象因素及其相关性

对平均气压等8项气象资料和每日发病人数，共计9个变量，两两进行相关分析，得到相关系数矩阵，如表1所示。

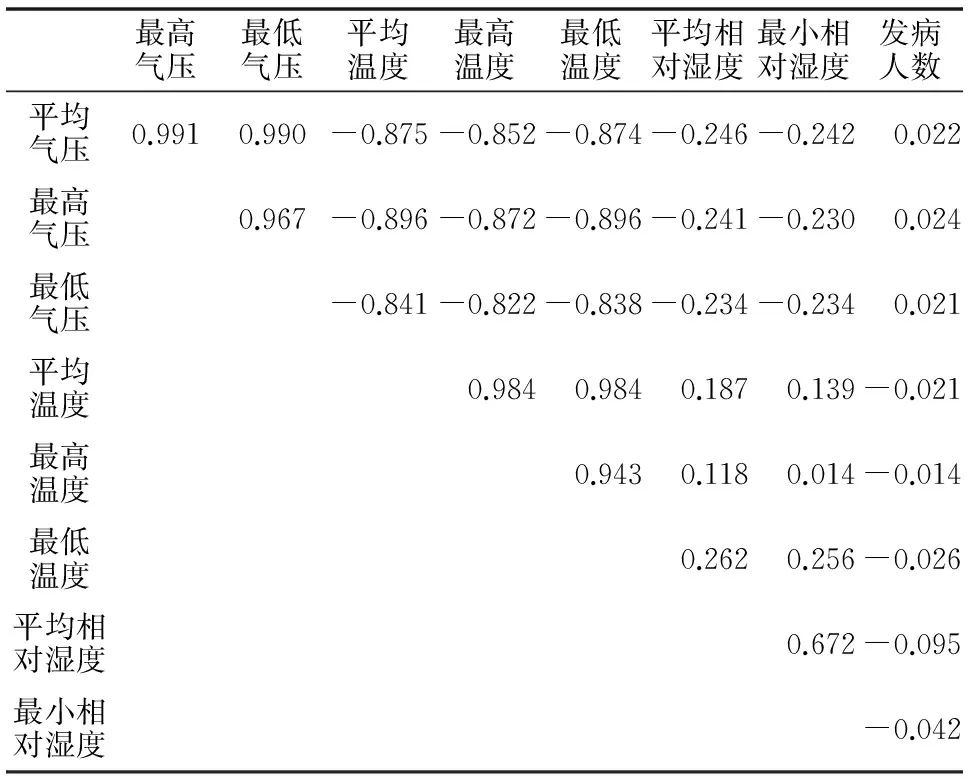
表1　气象原始数据的相关性分析

由表1可知，气象因素与脑卒中发病人数相关关系不显著，气象因素之间却高度相关。考虑到脑卒中发病人数这一时间数列受长期趋势、季节变动、周期变动和随机因素影响，判断数据随机因素对数据影响较大，因此采用365项“向前项移动平均”功能修匀数据，剔除随机因素和季节变动对数据的影响。

2.2影响脑卒中发病的人群特征及其描述统计

根据赛题中提供的某城市的脑卒中发病数据，分别从患脑卒中人群的年龄、职业、性别3个方面情况进行统计描述。性别、职业为定类尺度只能做频数分析，年龄为定量尺度除了做频数分析外还可以找平均数、标准差、众数、中位数、标准差系数等分析量。2.2.1对发病人群按职业、年龄段、性别作交叉表分析

运用SPSS软件的“描述统计”中“交叉表”功能，对发病人群按职业、年龄段、性别作频数分析，统计结果如表2所示。

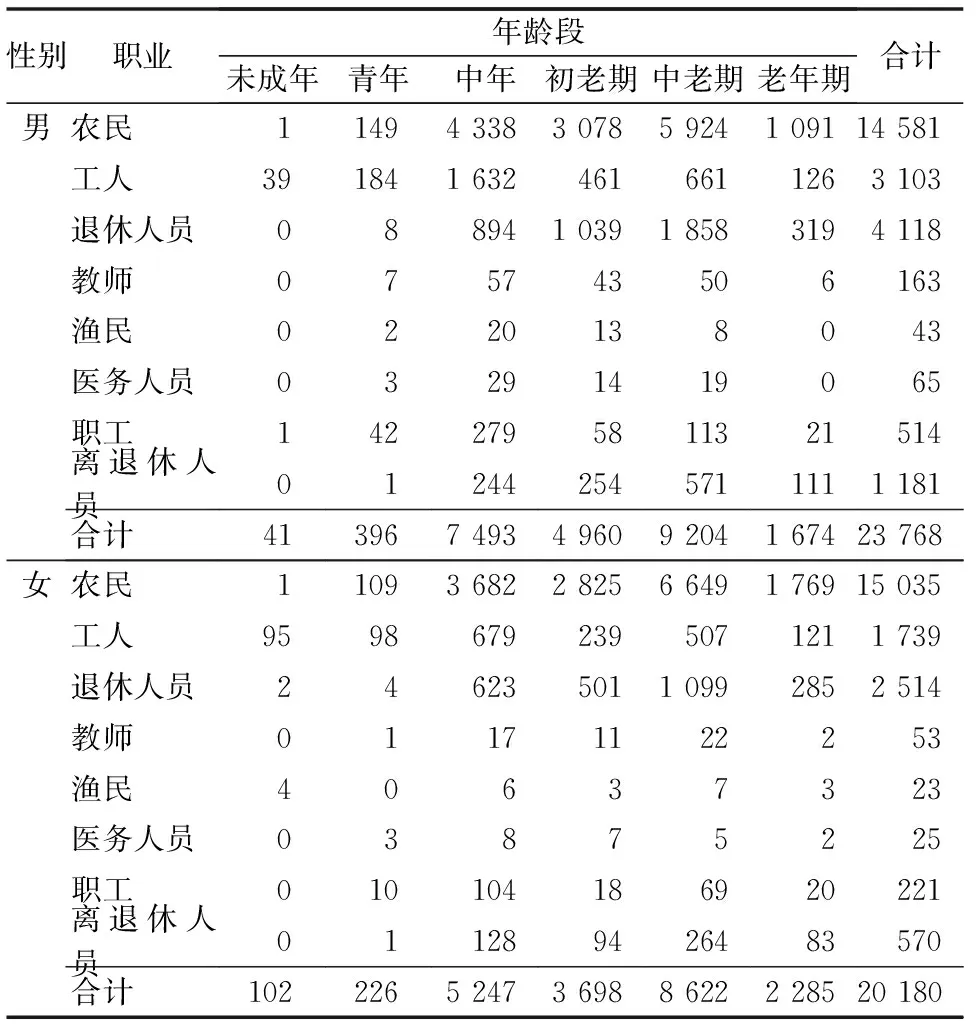
表2　按性别、职业、年龄段人数的描述统计　人

表2统计结果说明：1)农民在中年、初老期、中老期的发病人数都偏多，在所有职业中占很大的比例；2)工人的发病人数大部分集中在中年的时候。

2.2.2按性别、职业、年龄分别进行描述统计分析

按性别划分的发病人数描述统计：男性发病人数为23 768人，女性的发病人数为20 180人，说明男性脑卒中的发病概率高于女性，男性更应该注意对脑卒中的预防。

按职业划分发病人数描述统计：农民发病人数最多；医务人员、渔民的发病人数最少，说明脑卒中的发病与职业有一定的关联。

按年龄段划分发病人数描述统计：中老期患脑卒中的比例占所有年龄段的40.56%，说明中老期的人最容易患脑卒中；老年期亦是高发人群。

2.2.3按年龄段和延误治疗时间做交叉描述分析

对发病人群按年龄段和延误治疗时间作交叉描述分析，结果如表3所示。

表3　按年龄段划分的延误治疗时间统计描述　d

由表3可知：未成年人延误治疗时间最长，平均延误为113.48 d；延误治疗时间最短的是青年，平均延误24.97 d。

2.2.4按性别和延误治疗时间作交叉描述分析

对发病人群按性别和延误治疗时间做交叉描述分析，结果如表4所示。

表4　按性别划分的延误治疗时间统计描述　d

由表4可知：发病后，女性患者及时治疗优于男性患者。

2.2.5按职业和延误治疗时间做交叉描述分析

对发病人群按职业和延误治疗时间做交叉描述分析，结果如表5所示。

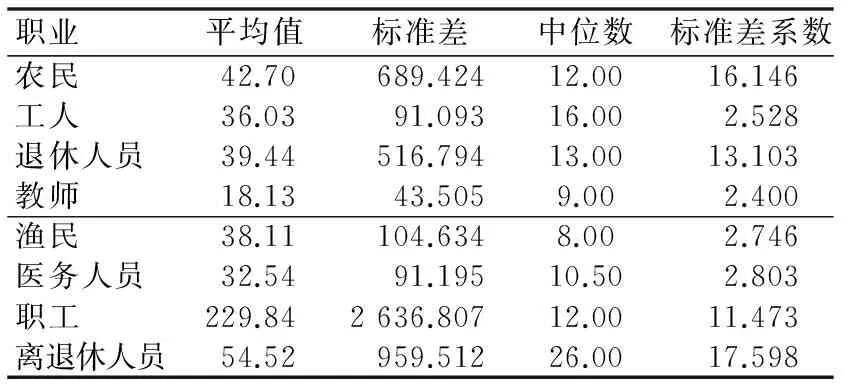
表5　按职业划分的延误治疗时间统计描述　d

由表5可知：职工延误治疗时间最长，平均延误为229.84 d；延误治疗时间最短的为教师，平均延误18.13 d，说明教师比较注重身体的保养。

2.2.6按发病月份划分进行描述统计

对发病人群按发病月份划分进行描述统计，结果如表6所示。

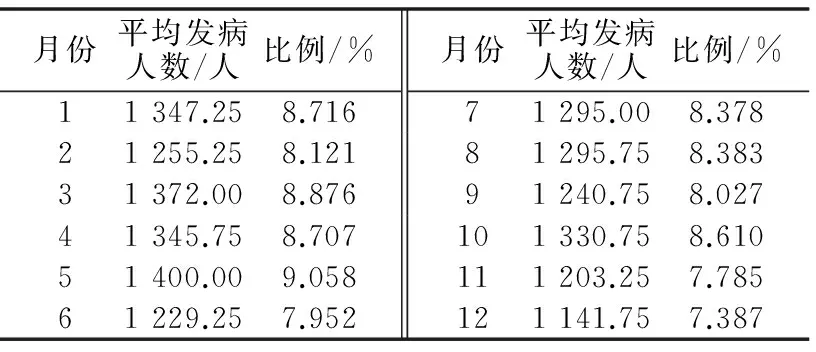
表6　按月份划分发病人数统计描述

由表6可知：5月份的平均发病人数最多，说明5月份的气象情况最容易引起脑卒中的病发。

2.2.7按发病年份划分进行描述统计

对发病人群按发病年份划分进行描述统计，结果如表7所示。

由表7可知：2009年的发病人数明显减少了，但是到了2010年发病人数又急剧上升。

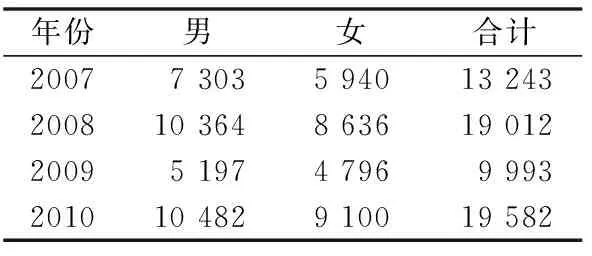
表7　按年划分发病人数统计描述　人

3脑卒中发病的气象影响因素多元线形回归分析

参阅相关资料，脑卒中的诱发原因与环境因素有关，包括温度、气压、相对湿度。已有的研究成果表明，寒冷天气、气压猛升是导致脑卒中的诱发因素[4]。脑卒中发病和气象因素有较强的线性关系。为此建立多线线性回归模型，分析影响脑卒中发病的气象因素。

3.1多元线形回归模型的建立

为更为准确描述脑卒中受气象因素影响的发病规律，整理气象资料和发病人数的时间数列，建立多元线性回归模型，得出脑卒中发病率与各因素之间的关系。

y=b0+b1x1+b2x2+…+bnxn+ε

(1)

其中：ε为随机误差项，且E(ε)=0；Var(ε)=σ2；b0,b1,b2,…,bn为常数项；y为发病人数(因变量)；x1,x2,…,xn为影响因素(自变量)，x1为平均气压，x2为最高气压，x3为最低气压，x4为平均温度，x5为最高温度，x6为最低温度，x7为平均相对湿度，x8为最小相对湿度。

3.2求解的方法及步骤

气象资料和发病人数的相关分析显示：自变量与因变量无明显规律性，自变量之间却高度相关。因此，建立多元线性回归模型时，如果过多地引入自变量会引起模型多重共线性缺陷，膨胀系数和容忍度超出允许范围。可以在回归分析求解时，通过选择改变自变量进入模型的方法，即选用“逐步回归”[5]，来预防多重共线性的出现。为此，运用SPSS软件，选择“分析”→“回归”→“线性”功能进行求解，在对话框中选择365项移动平均处理后的发病人数为因变量；平均气压、最高气压、最低气压、平均温度、最高温度、最低温度、平均相对湿度、最小相对湿度为自变量。使用“统计量”功能，选择模型拟合度、R方变化、描述性、部分相关和偏相关性、共线性诊断，得出分析结果。

3.3模型求解结果

模型留存气象变量的回归系数如表8所示。

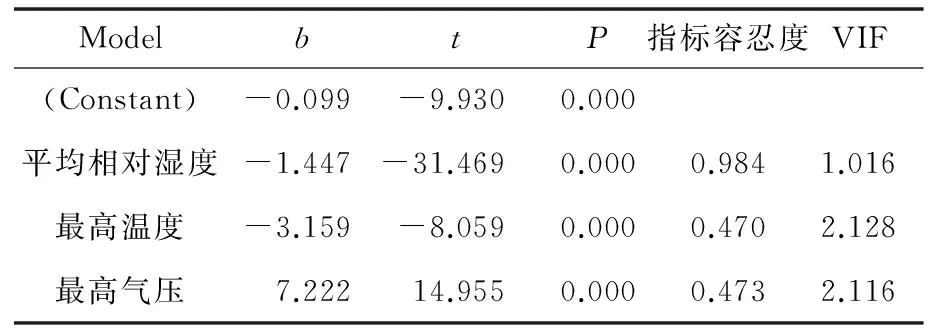
表8　回归系数

所得模型为：

y=-0.099+7.222x2-3.159x5-1.447x7

(2)

3.4模型检验

1)可决系数检验

对回归模型的拟合优度进行可决系数检验，结果如表9所示。

表9　模型汇总

通过上述分析，得到调整R方为0.616，说明模型能解释大多数数据，证明模型的拟合优度好。可决系数为0.617，表明多元线性回归模型解释了总体波动的61.7%，气象因素比较显著地影响了脑卒中的发病。调整R方为0.616，说明模型能解释大多数数据波动，模型的拟合优度好。

2)F-检验

对回归模型的整体显著性进行F-检验，结果如表10所示。

表10　方差分析表

根据方差分析表10，可知：P<0.05，所以拒绝原假设，即满足F-检验，说明多元线性回归整体具有显著性。

3)t-检验

由表8可知：模型中留存的气象因素的渐进显著性均为P<0.05，拒绝原假设，即通过t-检验，说明多元线性回归的系数显著，模型中留存的气象因素显著影响脑卒中的发病率。

4)共线性诊断

根据逐步回归的方法可以得到12组数据，由于多元回归分析变量会出现多重共线性，根据判定多重共线性的指标容忍度(Tolerance)越小越好和方差膨胀因子(VIF)在10以内越好，并且结合相关的资料，可以在众多数据中排除，以得到最显著的模型。由表8数据可知：VIF<10，且容忍度很小，所以可以判定出这种情况不存在多重共线性。

3.5模型结论

脑卒中发病与最高气压、最高气温和平均相对湿度满足以下多元线性回归模型：

y=-0.099+7.222x2-3.159x5-1.447x7

计算结果表明：发病人数与最高气温和平均相对湿度负相关，与最高气压正相关，即最高气温和平均相对湿度越低越容易得脑卒中，最高气压越高越容易得脑卒中。该结论与查询的相关文献资料情况符合，表示该模型结果比较准确，从数量角度验证了气象因素对脑卒中发病的影响。

4结语

本文利用SPSS软件统计分析患脑卒中人群基本数据，得出某些规律，该分析方法很好地反映出数据间的联系。在此基础上，剔除随机因素和季节变动的影响后，建立多元线性回归模型，采用“逐步回归”的方法消除多重共线性的影响，但是仍存在不可避免的缺陷，即根据数据无法确认是变量间否存在非线性数量关系，这一方面仍值得研究和改进。

参考文献：

[1] 王玉苏,陈佩宁,吴素敏.脑卒中发病环境因素分析及干预的数学模型[J].石家庄职业技术学院学报,2013,25(2):47-52.

[2] 张远,蔡磊,吴露.脑卒中发病环境因素分析及干预[J].南通职业大学学报,2013,27(3):64-67.

[3] 张明会.脑卒中发病环境因素分析及干预[J].广东技术师范学院学报,2014,35(11):78-83.

[4] 金爱兰,邱晓光.脑卒中与气象因素关系分析[J].医学信息,2004(9):525-527.

[5] 王黎明,陈颖,杨楠.应用回归分析[M].上海:复旦大学出版社,2008:74-76.

Statistical Analysis of the Influencing Factors of Cerebral Stroke

LIYi*

(Department of Information and Computing Science, Chengdu Technological University, Chengdu 611730, China)

Abstract:According to the data of the 2012 Mathematical Contest in Modeling, the patients with cerebral stroke from the gender, age, occupation, time of onset and diagnosis time are counted by using SPSS and the regularity and characteristics of stroke are investigated firstly. Next, a multiple linear regression model is found. At last, the conclusion is that the lower of the highest temperature and average relative humidity, and the higher of the highest air pressure are more susceptible for stroke.

Key words:Cerebral Stroke; statistical description; multiple linear regression

DOI:10.13542/j.cnki.51-1747/tn.2016.02.014

收稿日期：2016-04-15

基金项目：成都工业学院科研课题“时间序列分析在大学生数学建模竞赛中的应用”(KY1311021B)

作者简介：李一(1983— )，男(汉族)，山东滕州人，讲师、统计师，硕士，研究方向：统计学，通信作者邮箱：114467171@qq.com。

中图分类号：C812

文献标志码：A

文章编号：2095-5383(2016)02-0049-04