分数Black-Scholes模型下美式期权定价的切片法*

林汉燕　史旭明

(桂林航天工业学院　理学部，广西　桂林　541004)

分数Black-Scholes模型下美式期权定价的切片法*

林汉燕**史旭明

(桂林航天工业学院理学部，广西桂林541004)

摘要在市场股价满足分数Black-Scholes模型的条件下，以支付红利的美式看跌期权为例，应用切片法研究定价的近似计算，得到一般算法。

关键词分数Black-Scholes模型；美式期权；切片法

美式期权是持有人可以在合约规定的到期日前任一个工作日实施的期权，但何时实施获利最大未知，所以通常情况下不能得到价格解的解析式(除永久美式期权外)。目前有关美式期权定价的研究成果很多[1-5]，但这些成果由于基于Black-Scholes模型假设，所以与实际股价运动不符，需要更接近股价运动的驱动模型。分数Black-Scholes模型就是其中的模型之一。本文在分数Black-Scholes模型下，应用切片法研究Hurst参数H>1/2的红利连续支付的美式看跌期权定价问题。切片法是根据Carr p[6]提出的利用有限差分法，结合二次近似的思想来计算的近似法。 G.H.Meyer和J.Van der Hoek[7]、Gu yong geng[8]、姜礼尚[9]等都在经典Black-Scholes模型下用切片法研究了美式期权定价，得到较好结果。本文将这种算法应用到分数Black-Scholes模型中。

1分数Black-Scholes模型

定义设(Ω,F,P)是一个完备概率空间，H∈(0,1)，称一个连续高斯过程BH={BH(t)；t≥0}是Hurst参数为H的分数布朗运动，如果它满足：

(1)BH(0)=E(BH(t))=0，(t>0)

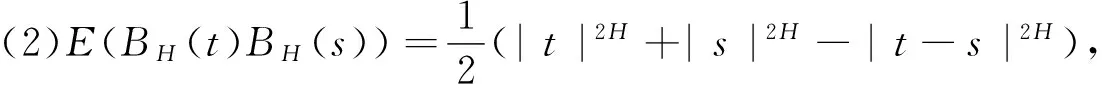
假设(Ω,F,Ft,P)是一个具有σ-流的{Ft，t≥0}完备概率空间,Ft是由F生成的自然σ代数流。在金融市场中仅有两种资产，一种为有红利支付的风险资产，价格S(t)适合方程：

dS(t)=(μ(t)-q(t))S(t)dt+σS(t)◇dBH(t) ，

(1)

其中μ=μ(t)表示股价期望回报率，q=q(t)表示红利率，σ≠0表示股价瞬时波动率(常数)，BH(t)表示分数布朗运动，“◇”为Wick积分。

另一种资产为无风险证券，价格A(t)满足

dA(t)=r(t)A(t)dt

(2)

其中r=r(t)为无风险利率。

这两种资产交易连续，交易时间为[0，T]，不支付税收和交易费用，借款和存款利率相等，可以买空卖空。(1)、(2)就是分数Black-Scholes模型，它是无套利的完全市场模型。

在分数Black-Scholes模型下，执行价格为K，到期日为T的美式看跌期权价格P=P(s,t)对应下列定解问题：

(3)

其中S*=S*(t)是最佳实施边界函数，r、q均为常数。

2切片法

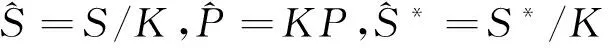
(4)

其中0≤n≤N-1。

算法如下：

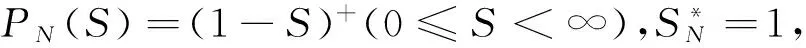
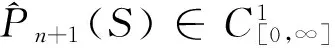
(5)

Pn(S*)=1-S*

(6)

(7)

Pn(S)→0(S→∞)

(8)

(d)求解常微分方程自由边界问题(5)-(8)。

(9)

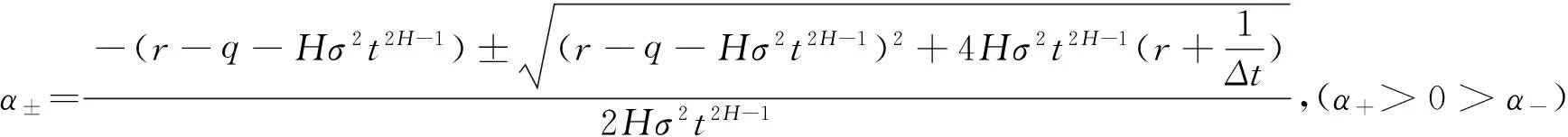
LΔPN-1=0(1≤S<∞)

(10)

(11)

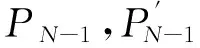
(12)

以及适合边界条件(6)-(8)。

在 [0，∞)上，PN-1(S)由三个分段函数组成，其中α+，α-是特征方程(9)的根。求右端为PN-1(S)的非齐次微分方程的特解，考虑引理1：

引理1[9]设非齐次方程

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

PN-2(S)→0(S→∞)

(21)

方程(16)有特解

(22)

由引理1，方程(14)、(15)的特解为

(23)

(24)

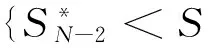
(25)

(26)

(27)

由(21)得

(28)

由(17)得

(29)

(30)

W3(1)=0

由(29)、(30)得

(31)

由(18)得

(32)

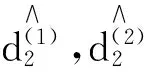
(33)

由自由边界条件(20)、(21)得

(34)

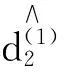
(35)

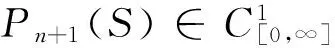
(36)

(37)

……

(38)

(39)

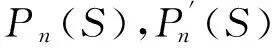
(40)

……

Pn(S)，P′n(S) 在S=1处连续

(41)

(42)

(43)

Pn(∞)=0

(44)

Pn(S)具有下述形式：

要得到右端形如Sα±(lnS)j的非齐次常微分方程特解，需要引理2。

引理2[9]考虑非齐次方程

(45)

其中ω是特征方程(9)的单根，即

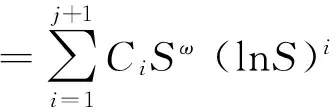
3结束语

从上面推导可以得到用切片法计算美式期权的一般过程。切片法在计算中所有的算式都是显示式，不需要解大型线性方程组，但计算比较繁琐，需要结合其他方法，使计算速度和精度提高。

参考文献

[1]张铁. 美式期权定价的数值方法[J]. 应用数学学报, 2002, 25(1)：113-122.

[2]张铁. 美式债券期权的有限元方法[J]. 计算数学, 2004, 26(3)：277-284.

[3]吴建祖,宣慧玉. 美式期权定价的最小二乘蒙特卡洛模拟方法[J]. 统计与决策, 2006(1): 155-157.

[4]Geske R, Johnson H. The American put option valued analytically [J]. Journal of Finance,1984 (39):1511-1524.

[5]Macmillan L W. Analytic approximation for the American put option [J]. Advances in Futures and Options Research, 1986(1): 119-139.

[6]Carr P. Randomization and the American put [J]．The Review of Financial Studies, 1998, 11(3):597-626．

[7]G H Meyer, J Van der Hoek. The Evaluation of American Options with the method of Lines [J]. Advances in Futures and Options Research, 1997, 9: 265-285.

[8]Gu yong geng. A new numerical method on American Options pricing [J]．Science in China (F), 2002, 45(3):181-188.

[9]姜礼尚. 期权定价的数学模型和方法[M]. 北京：高等教育出版社, 2003:182-192.

(责任编辑骆桂峰)

* 基金项目：广西教育厅科研项目《分数布朗运动模型下几种奇异期权的定价》(YB2014436)。

** 作者简介：林汉燕，女，广西贵港人，副教授。研究方向：金融数学。

中图分类号：O211.6

文献标志码：A

文章编号：2095-4859(2016)01-0070-06