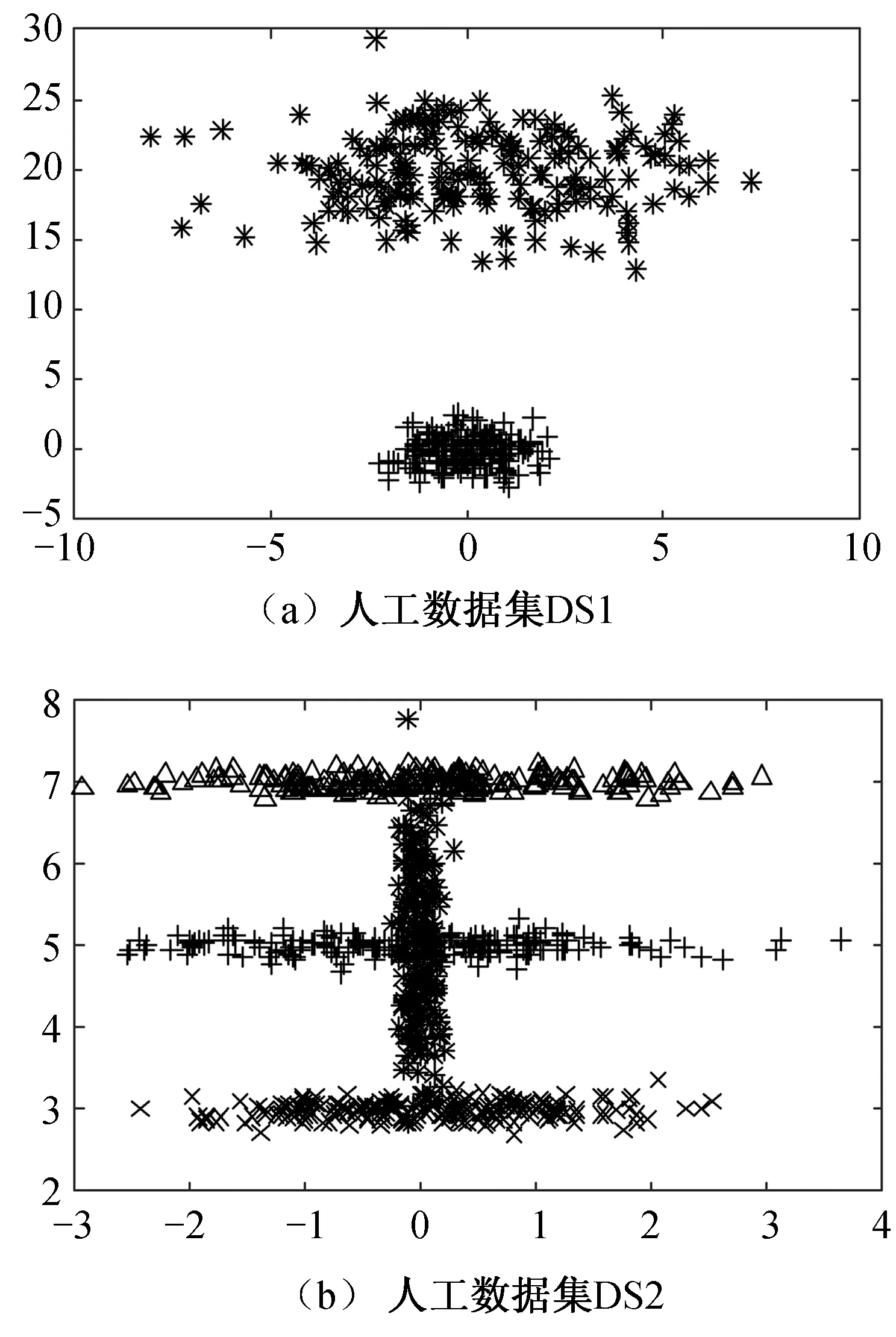
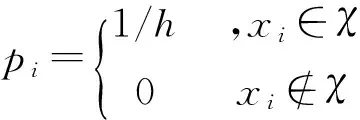基于MCD初始化的高斯混合模型聚类*
2016-06-27胡庆辉阮晓霞
胡庆辉 阮晓霞
1 桂林航天工业学院 计算机科学与工程系,广西 桂林 541004;2 桂林航天工业学院 外语外贸系,广西 桂林 541004
基于MCD初始化的高斯混合模型聚类*
胡庆辉1阮晓霞2
1桂林航天工业学院计算机科学与工程系,广西桂林541004;2桂林航天工业学院外语外贸系,广西桂林541004
摘要高斯混合模型聚类是一种基于概率模型的有效聚类方法,传统算法对模型的初始化(包含成分数、每个成分的均值和方差)的设置非常敏感,容易导致EM算法陷入局部最优解或收敛到解空间的边界,为了解决这个问题,可利用最小化协方差矩阵行列式(MCD), 结合传统成熟的高斯混合模型算法,来实现对高斯混合模型的初始化,而MCD初始化的算法对初始值的设定没有特殊的要求,通过实验证明其具有很好的聚类性能和鲁棒性。
关键词高斯混合模型;聚类;最小协方差矩阵行列式;EM算法
有限概率混合模型是进行聚类和密度估计的一种非常有效的数学方法之一。它通过利用有限个独立概率模型的线性凸组合,来刻画一个复杂的数据分布。相对于单个模型,混合模型有更强的可解释性和表达能力。目前,有限混合模型已经得到了广泛的应用,如语音识别[1]、医学研究[2]、图像中的人脸肤色区域检测等。
在选择有限概率混合模型进行数据分析时,需要假设数据服从某种概率分布。根据中心极限定理,对于大量相互独立的随机变量,其均值分布以正态分布为极限,即大量随机变量之和近似服从高斯正态分布,因此概率混合模型通常假定数据服从混合高斯分布[1-4],即高斯混合模型。在该假定条件下,模型中的每个成分都服从各自的高斯分布。但是高斯混合模型对噪声非常敏感,对于含有大量噪声的数据,高斯混合模型通常达不到理想的建模效果,这时可以选择具有重尾的t分布[5-6]来代替高斯分布。另外,针对不同的实际应用,还可以选择皮尔逊分布[7]、Dirichlet分布[8-9]等。
聚类任务中所使用的观测数据是不完整的,期望最大化的EM算法可以通过迭代使用观测到的数据量来估计不可观测的数据量。 因此,在利用有限混合模型进行聚类时,通常采用EM算法求解未知标记的最大似然值,EM算法的优点是简单稳定,但是收敛过程比较缓慢,并且通常使参数陷入局部最优值。对于有限概率混合模型来说,模型中各成分的初始化参数如果设置不当,则很容易使算法收敛到一个比较差的局部最优解。因此如何设置混合模型的参数对算法的性能是非常重要的。为此,在文献[10]中,作者有针对性地讨论了EM算法的初始化方法,文献[11-12]中,作者针对混合模型的成分估计进行了研究。针对算法的鲁棒性问题,文献[4]中作者提出了一个最小信息长度(MML) 收敛准则,一定程度上提高了EM算法的鲁棒性,但是该算法仍然可能会因为初始成分的设置不同而收敛到不同的次优解。文献[3]中,作者设置了成分数初值直接等于观测值个数,通过对成分的混合系数施加熵惩罚因子,在迭代中根据一定准则快速自动减少成分数目,大量实验证明该算法具有很好的鲁棒性。但是该算法只适合于观测值较少的情况,随着观测值数量的增大,该算法的效率会因为初始成分数太大而大大降低。因此,使算法在较少迭代次数内快速降低成分数目是一个有效提高该算法效率的办法。
本文针对文献[3]的算法,提出了利用最小化协方差矩阵行列式(Minimum Covariance Determinant Estimator ,MCD)进行该算法的成分初始化及相应的参数设置,MCD是一个鲁棒的多变量散布估计算法[13],对于给定的数据集,MCD的目标是寻找该数据集一个子集,使得子集的协方差矩阵的行列式最小。我们通过迭代调用MCD来获取混合模型的成分数和每个成分的参数值。由于通过MCD初始化大大减少了文献[3]的初始成分数,使得算法的执行速度有很大提高,同时通过实验表明,用MCD初始化的算法仍然具有很好的鲁棒性,算法的精度也没有降低。
1高斯混合模型及优化算法
混合模型的密度函数可表示为c个概率密度函数(也叫做成分)的线性组合形式:
(1)
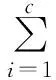
(2)
其中μi和Σi分别为第i个成分的均值向量和协方差,δ(x,μ;Σ)表示x与μ的Mahalanobis距离。

L(ω,μ,Σ;x1,x2,...xn)
(3)
在公式(3)中,针对未知参数zki,可以使用EM算法进行求解。该算法分为以下两步:
E-Step:求解参数zki:


(4)
M-Step:对(3)式的μk、Σk和ωk求最大,有:
(5)
(6)
(7)
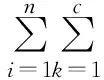
(8)
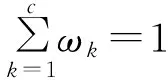
求解公式(8),得到ωk第t+1次迭代的更新公式为:
(9)
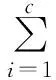
(10)
(11)
2基于MCD高斯混合模型优化算法
2.1最小化协方差矩阵行列式(MCD)
MCD是一个鲁棒的多变量散布估计算法[13],对于给定的数据集χ,MCD的目标是寻找一个子集ε⊆χ,使得ε的协方差矩阵的行列式最小。然后可以用ε的协方差矩阵作为χ的协方差矩阵。MCD具有仿射同变性质,即使在有外样本干扰的情况下,也能够获得比M估计和S估计更好的估计值。其基本原理的数学描述如下:
设输入的d维样本集为χ={x1,x2,...xn|x∈Rd},选择h (12) (13) (14) MCD是NP问题,在文献[14]中,作者提出了改进的Fast-MCD算法,大大改进了算法的执行效率,使得MCD方法能够应用在各种稳健估计中。 2.2利用MCD初始化高斯混合模型 算法1:初始化高斯混合模型的参数输入:数据集χ={x1,x2,…,xn|x∈Rd},初始样本子集大小h≪N;输出:成分数ck,每个成分的参数θk(包含了均值μk和协方差Σk)1.初始化k=1,χk=χ;2.WHILE |χk| 新生成的子集可以与已生成的子集产生交叉,但是不能包含原有的子集,否则新的子集大小h折半,然后重新生成子集,直到所有的样本都有属于特定的子集为止。minNum为每个子集的最少样本数,当|χk|小于minNum时,不需要再产生新的成分,而是直接将剩余的|χk|个样本分别分配到距离该样本最近的成分中。 2.3基于MCD高斯混合模型算法 针对文献[3],基于MCD初始化算法的基本步骤如下: 算法2:基于MCD初始化的高斯混合模型算法输入:数据集χ={x1,x2,…,xn|x∈Rd},初始样本子集大小h≪N;输出:概率密度函数f(x;ω,θ);1.初始化,需要做一下工作:(1)惩罚系数β=1;(2)利用算法1初始化成分个数c及每个成分的协方差矩阵Σk和均值向量μk;(2)初始化zki;2.REPEAT 利用公式(9)计算混合系数ωk,如果ωk<1/n,则删除成分k,同时执行(10),(11); 利用(7)计算协方差矩阵Σk; 利用(4)计算zki; 利用(6)计算均值向量μk;UNTIL max1 3实验分析 本文针对3个算法进行了实验比较,分别来自文献[3]的CA1、文献[4]中的CA2以及本文的算法CA3,对于本文中的算法,利用MCD进行成分初始化时,设置h为样本数的1/10,minNum=10,即每个初始成分的样本数不少于10个。实验环境为Windows 8 64位操作系统,Intel(R) Core(TM)i5 2.80 GHz,16 GB内存,仿真软件为Matlab7.10.0.499。 实验分别在多个人工数据集和真实数据集上完成。 3.1 人工数据集的比较结果 图1 两个人工数据集的数据分布 每种算法执行20次,每次随机生成测试样本,最后得到在两个人工数据集上的比较数据如表1所示: 表1 人工数据集的比较结果 3.2真实数据集上的比较结果 本组实验采用的真实数据集是来自文献[15]的跳蚤甲虫数据,数据集大小为74,包含了3个物种,分别是concinna(Con)、heikertingeri(Hei)及hetapotamica(Hep); 每个样本包含了2个特征值,分别是阳茎前端的最大宽度和前端夹角(其中1单位=7.5°)。采用3种算法进行聚类,随机执行20次后,平均结果的比较数据如表2所示。 表2 真实数据集的比较结果 由表1和表2可以看出,CA2算法的聚类性能相对比较差,且通常会花费较多的迭代次数和时间,本文算法CA3经过MCD成分初始化后,EM算法的迭代次数及所耗费的时间都比文献[1]中的CA1算法有大幅度降低,这是因为CA2的初始成分数通常不会超过40,CA1的初始成分数是样本个数,远远超过了CA2的初始成分数,而算法每次迭代所耗费的时间与成分数呈指数增长关系,因此通过MCD方法降低初始成分数后,可以大大加快算法的执行速度,而在分类结果方面,CA3相对于CA1并没有明显的变化。这表明本文提出的经过MCD初始化的高斯混合模型聚类算法不仅具有很好的鲁棒性,同时还具有较快的收敛速度。 4结束语 本文针对文献[3]中提出的混合模型聚类算法,提出了一种利用最小协方差行列式(MCD)进行成分初始化的方法,MCD是一个鲁棒的多变量散布估计算法,能够很好地应用于多变量散布估计,通过迭代调用MCD来获取混合模型的成分数和每个成分的参数值,这些成分能够很好地反映数据的分布情况。由于通过MCD初始化大大减少了文献[3]的初始成分数,使得算法的执行速度有很大提高,同时通过实验表明,用MCD初始化的算法仍然具有很好的鲁棒性,算法的精度也没有降低。 参考文献 [1]Reynolds DA, Rose RC. Robust text-independent speaker identification using Gaussian mixture speaker models[J]. IEEE Transactions on Speech and Audio Processing, 1995,3(1):72-83. [2]Ferreira da Silva AR. A Dirichlet process mixture model for brain MRI tissue classification[J]. Medical image analysis, 2007,11(2):169-182. [3]Yang M S, Lai C Y,Lin C Y. A robust EM clustering algorithm for Gaussian mixture models[J]. Pattern Recognition, 2012,45(11): 3950-3961. [4]M A T Figueiredo, A K Jain. Unsupervised learning of finite Mixture models[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002(24):381-396. [5]Jeffrey L Andrews, Paul D McNicholas. Model-based classification via mixtures of multivariate t-distributions[J]. Computational Statistics and Data Analysis, 2010(6): 520-529. [6]Peel D, McLachlan G J. Robust Mixture Modeling using the t Distribution[J]. Statistics and Computing, 2000(10): 339-348. [7]Jianyong Sun, Jonathan M. Garibaldi. Robust mixture clustering using Pearson type VII distribution[J].Pattern Recognition Letters, 2010(7):1-8. [8]Bouguila N,Ziou D,Vaillancourt J. Unsupervised learning of a finite mixture model based on the Dirichlet distribution and its application[J]. IEEE Transactions on Image Processing, 2004 (11): 1533-1543. [9]Bouguila N,ElGuebaly W. Discrete data clustering using finite mixture models[J]. Pattern Recognition, 2009(1): 33-42. [10]C Biernacki,G Celeux,G Govaert. Choosing starting values for the EM algorithm for getting the highest likelihood inmultivariate Gaussian mixture models[J]. Computational Statistic&Data Analysis, 2003(41): 561-575. [11] K Reddy, H D Chiang, B Rajaratnam. TRUST-TECH-based expectation maximization for learning finite mixture models[J]. IEEE Transactionson Pattern Analysis and Machine Intelligence,2008(30):1146-1157. [12] Richardson, P J Green. On Bayesian analysis of mixtures with an unknown number of components[J]. Journal of the Royal Statistical Society-SeriesB,1997(30): 731-758. [13] P Rousseeuw, A Leroy. Robust Regression and Outlier Detection[M].JohnWiley&Sons Inc,1987. [14] Peter J Rousseeuw, Katrien Van Driessen. A Fast Algorithm for the Minimum Covariance Determinant Estimator[J]. Technometrics, 1999,41(3):212-22. [15]A A Lubischew. On the use of discriminant functions in taxonomy[J]. Biometrics, 1962,18: 455-477. (责任编辑陈葵晞) * 基金项目:广西高校科研重点项目《基于多核学习的半监督支持向量机相关技术研究》(ZD2014147); 桂林航天工业学院科研项目《监督机器学习中的数据降维方法研究》(Y12Z028)。 作者简介:胡庆辉,男,重庆开县人。 副教授, 博士。 研究方向: 机器学习,智能计算。 中图分类号:TP301.6 文献标志码:A 文章编号:2095-4859(2016)01-0001-06