“鸡兔同笼”问题与数学模型
2016-06-27周志胡重光
周志 胡重光
“鸡兔同笼”问题与数学模型
周志胡重光

“鸡兔同笼”问题是中国古代著名趣题。这个问题最早见于成书约在1500年前的《孙子算经》:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”[1]意思是:有若干只鸡兔关在同一个笼子里,从上面数有35个头,从下面数有94只脚。问笼中各有几只鸡和兔?
由于它奇特有趣,我国的小学数学教材历来都在“典型应用题”中教学这个问题。现在的人教版新课标小学数学实验教科书则把它作为“数学广角”的一个内容。但是,有人认为,“鸡兔同笼”问题纯属虚构,没有应用性,解答该问题的假设法也没有普遍意义,因此属于过时的落后的数学问题,没有什么价值。
这些观点正确吗?本文将做一点深入的探讨。
一、“鸡兔同笼”问题的解法
首先我们以下面的题目为例探讨“鸡兔同笼”问题的解法。
例1一些鸡和一些兔子关在同一只笼子里。从上面数有20个头,从下面数有52条腿。问鸡兔各有几只?
1.假设法
这是最常用的解法,众所周知,毋庸赘述。
2.减腿法
这个方法被认为是最简单的,书上没有给它命名,为了方便,本文给它取了这个名字。
解法:让每只鸡和兔都抬起两条腿,这样笼子里的腿就减少了40条,而剩下的12条腿全是兔子的,并且每只兔子只有2条腿。所以兔子是6只。
用第一种解法,教学实践证明,小学高年级学生也有相当一部分难以理解。而第二种方法的最大问题是:你是怎么想到它的?
如果“鸡兔同笼”问题只有这两种解法,它的价值确实要大打折扣。但事实并非如此。
3.画图法
画图分析:画20个小圈代表20个头。先在每个头上都画2条腿,共得40条腿。还差12条腿,再在一些头上又添2条腿,添了6个头后,恰好添够12条腿,并且总共凑足52条腿(如图)。

从图中可以看出,4条腿的有6只,2条腿的有14只。因此,笼中共有6只兔子,14只鸡。
这种解法具体形象,具有可操作性,符合儿童的认知规律,小学低年级学生也能理解。并且解答的过程就是假设法的形象化,因此能为学习假设法打下基础。
4.列表法
仍以例1为例,教师列出下表。
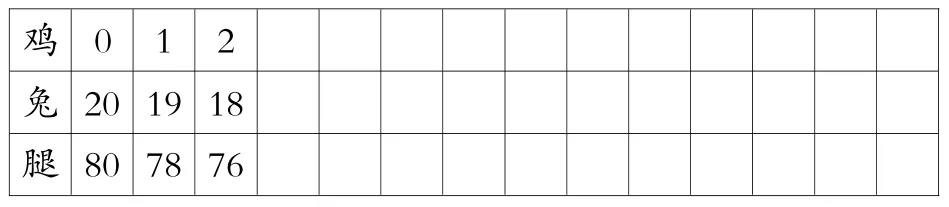
鸡 0 1 2 兔20 19 18 腿80 78 76
这个表只填出头3列,后面的让学生接着填。下面的表是按照最慢的步调填的,实际上学生填几个数后一般就会跳跃着填,通过多次尝试就会发现规律,进而改进方法,速度就会快很多。因此教学时要给充分的时间让学生自主探索。
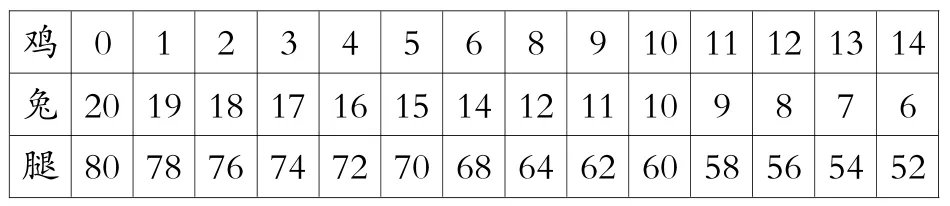
鸡 0 1 2 3 4 5 6 8 9 10 11 12 13 14兔 20 19 18 17 16 15 14 12 11 10 9 8 7 6腿 80 78 76 74 72 70 68 64 62 60 58 56 54 52
用列表的方法解,一是儿童容易理解,二是能看出鸡兔腿数的变化过程。这种方法不但能为儿童理解假设法打下基础,而且渗透了函数的思想,对发展儿童的数学思维大有好处。
这两种解法大大提高了“鸡兔同笼”问题的数学教育功能,使“鸡兔同笼”问题成为小学数学的良好教学内容。
二、“鸡兔同笼”问题的变式
“鸡兔同笼”问题还有大量的变式,例如:
1.鸡兔同笼,共有15只头,鸡腿比兔腿多12条。求鸡兔各几只?
这些变式表明,“鸡兔同笼”问题的内容是相当丰富的。
例2蜘蛛有8条腿,蜻蜓有6条腿和2对翅膀,蝉有6条腿和1对翅膀。现在有这三种小虫共18只,它们共有118条腿和20对翅膀,问每种小虫各有几只?
分析和解答:这道题条件比较复杂,为了便于分析,先将条件列表整理如下:
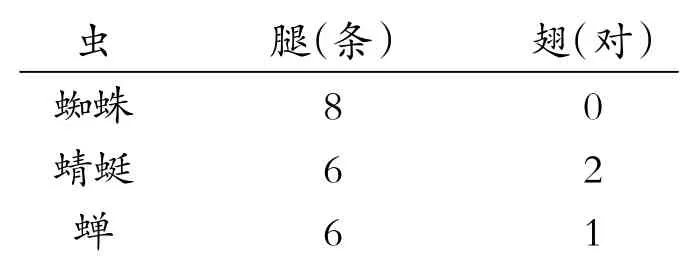
虫蜘蛛蜻蜓蝉腿(条) 翅(对)8 6 6 0 2 1
从表中可以看到,蝉和蜻蜓都是6条腿,因此可以把它们统一起来,都当作“六足虫”,而不考虑翅膀这个条件。这样问题就简化为:
八足虫和六足虫共18只,共有腿118条,两种虫各有几只?
这是典型的“鸡兔同笼”问题,用假设法容易求得,八足虫(蜘蛛)有5只,六足虫(蜻蜓和蝉)有13只。
下面再求蜻蜓和蝉各有几只。这时问题又转化为:
“二翅虫”和“一翅虫”共13只,共有翅膀20对,两种虫各有几只?
这又是简单的“鸡兔同笼”问题,再次使用假设法得蜻蜓(二翅虫)有7只,蝉(一翅虫)有6只。
三、“鸡兔同笼”问题的推广
以上关于“鸡兔同笼”问题的变式虽然揭示了许多新的数量关系,但这些问题仍然是虚构的,不具有应用性。然而“鸡兔同笼”问题还可以推广。下面举几个例子。
例3学校买大小椅子共20把,共用960元。大椅子每把60元,小椅子每把40元。大小椅子各买了多少把?
这道题虽然没有鸡、兔,但数量关系与“鸡兔同笼”问题完全相同,可以用假设法来解。
例4上山、下山共走19千米,共用5小时。上山的速度是每小时3千米,下山的速度是每小时5千米。上山、下山各走了几小时?
这道题也是“鸡兔同笼”问题,可以用假设法解:假设全是上山路或全是下山路。
例5一项工程,甲队独做需6小时完成,乙队独做需10小时完成。现在甲队做若干小时后,因另有任务由乙队接着做,合起来共用了7小时做完。问甲队做了几小时?
这道题也可以转化为“鸡兔同笼”问题。把这项工程平分为30份,那么甲队每小时做5份,乙队每小时做3份,合起来共用了7小时做完,求甲队做了几小时。“翻译”成“鸡兔同笼”问题就是:甲、乙两种动物共有30条腿、7个头。甲动物有5条腿,乙动物有3条腿。问甲动物有几只?
以上3例都没有鸡、兔,但数量关系与“鸡兔同笼”问题相同,并且都是生活、生产中广泛存在的问题。由此看来,“鸡兔同笼”问题虽然是虚构的,但其数量关系却是现实的,并非没有应用性。
不仅如此,有的问题尽管与“鸡兔同笼”问题的数量关系不同,但也可以用假设法解。
比实际多卖出:240-188=52(千克)。
例7甲、乙、丙三种笔记本的定价分别为每本2元、3元和7元,三种笔记本共买了47本,共用了212元。其中乙种笔记本购买的本数是甲种笔记本的2倍。三种笔记本各买了多少本?
分析和解答:假设三种笔记本的定价都是7元,那么47本共需:7×47=329(元)。
比实际情况多用了:329-212=117(元)。
拿出3本7元的,换入2本3元的、1本2元的(因为乙种笔记本是甲种笔记本的2倍),可以减少:7×3-(3×2+2)=13(元)。
要减少117元需要换:117÷13=9(次)。
因此,丙种笔记本有:47-3×9=20(本),乙种笔记本有:9×2=18(本),甲种笔记本有:9×1=9(本)。
这两个例子表明,假设法不仅是一种解题方法,更是一种思维策略,即首先将复杂的问题简化,然后作调整。它不仅能用于“鸡兔同笼”问题,还能用于许多其他实际问题。
四、“鸡兔同笼”问题的意义
由以上的介绍和分析可以看到,“鸡兔同笼”问题有以下意义。
1.数学教育意义
“鸡兔同笼”问题的多种解法分别适用于小学各年级的儿童,具有趣味性、可操作性和思考性,能培养儿童的数学兴趣,发展儿童的数学思维。
2.思维策略意义
解答“鸡兔同笼”问题的假设法是一种思维策略,其基本思想是“以退为进”,符合华罗庚所说的:善于“退”,足够地“退”,“退”到最原始而不失去重要性的地方,是学好数学的一个诀窍!因而具有重要的思维价值和广泛的现实意义。
3.数学思想意义
中国古代数学最讲究实用,出现“鸡兔同笼”这种纯属虚构的问题,初看起来似乎颇有些奇怪。然而从上面的例子可以看出,古人虚构这个问题的目的是为了给出一个数量关系的模型,凡是能够套上这个模型的问题,都可以用假设法来解。也就是说,“鸡兔同笼”问题体现了数学模型的思想。这一点在现代数学中具有重要意义。
20世纪中叶,随着现代数学的发展和电子计算机的诞生,建立数学模型日渐成为数学的主要目标之一。1998年,时任世界数学联盟主席的D.Mudford在论述现代数学的发展趋势时说:“创建好的模型正如证明深刻的定理一样有意义。我想,承认这一点,数学将会从中受益。”[2]
在发达国家,数学模型的思想方法已进入中小学数学教学。美国的小学数学教材编入了大量的关于数学模式和模型的教学内容。从以上的介绍和分析可以看到,“鸡兔同笼”问题作为一种数学模型,具有生动有趣、易于理解和接受的特点,可以说是我国数学教育得天独厚的资源。类似的还有盈亏术、百鸡术、求一术等。恰当地利用这类古代的问题,可以为数学模型的教学独辟一条具有民族特色的蹊径。
我国著名数学家吴文俊先生指出,中国古代数学的特点是:从实际问题出发,经过分析提高,再抽象出一般的原理、原则和方法,最终达到解决一大类问题的目的。①“鸡兔同笼”问题鲜明地体现了这一特点。吴文俊先生并认为,“将来的数学,应该是走中国古代数学的道路,而不是国际道路,这是一条总的趋势”。②
由此看来,研究中国古代数学的思想方法,特别是挖掘中国古代数学在数学教育方面的作用和意义,应该是我国数学和数学教育工作者责无旁贷的重要任务。
(作者单位:长沙市实验小学湖南第一师范学院)
参考文献
[1]李俨,钱宝琮。李俨钱宝琮科学史全集(第一卷)[M]。沈阳:辽宁教育出版社,1998。
[2]刘兼,孙晓天。数学课程标准解读[M]。北京:北京师范大学出版社,2002。
注释
①见《百度百科·吴文俊》。
②CCTV10大型人物访谈节目:《大师讲科普》——吴文俊,2008-01-28。
