恒力系统的设计计算

唐久昌

摘 要：建立恒力系统的数学模型，依据系统的工作原理和几何模型进行受力分析，推导出平衡系统中节点运行的曲线轨道方程，并结合MATLAB程序及PROE工程软件绘制轨道曲线，为恒力系统中的轨道曲线提供了一套完整的参数化设计方法。

关键词：恒力系统；设计计算；数学模型；轨道曲线

中图分类号：TM205+.2 文献标识码：A DOI：10.15913/j.cnki.kjycx.2016.12.018

教育机构、培训机构在使用展示板进行人工教学的过程中，需要按照不同的需求便捷地移动展示板，同时保持任意位置平衡，便可轻松操作，将展示板上升或下降到指定的任意位置。恒力机构是一种承受悬挂力不随受力方向位移变化而变化的柔性顺滑的受力系统，即在外部作用保持不变的情况下，一次性调节主弹簧弹力，使其允许位移在一定的范围内变化，无需外力作用能保持在预定的任意位置的机构。现阶段，我国使用较多的为连杆式拉伸弹簧或者刀型凸轮与压缩弹簧的恒力系统，以及凸轮恒力矩机构。这几种均依据力矩平衡原理设计。本文采用拉伸弹簧辅以平衡系统，平衡系统采用曲线轨道对辅弹簧受力进行处理，以满足对主弹簧的受力补偿，达到合力保持定值，提供恒力输出。

弹簧恒力系统具有以下优点：①结构完全对称，无产生干扰的外力，运行平滑、顺畅、稳定；②采用拉伸弹簧，稳定性高，易于制造；③精度高、受力范围广、调节方便、应用范围广。

1 恒力系统的工作原理

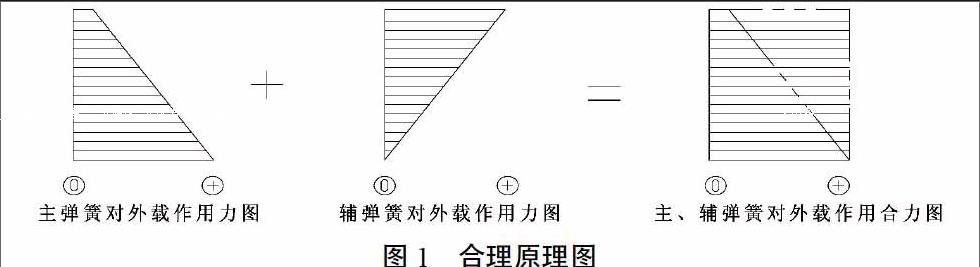
1.1 主、辅拉伸弹簧的合力原理图

主、辅拉伸弹簧通过平衡系统形成合力保持恒定值，建立如图1所示的合力原理图。

1.2 恒力系统的力学模型结构原理

1.2.1 恒力系统的设计理念

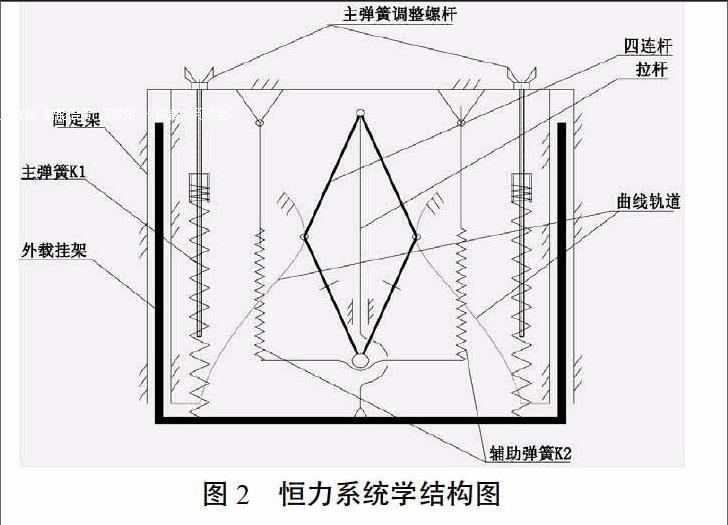
弹簧恒力系统采用合力为恒定值的设计理念，主弹簧为外载提供主要的拉力。由于拉伸弹簧的变形与拉力呈线性的表象，因此不能满足恒力的要求。如果采用拉伸弹簧向外负载提供恒定的拉力，这需要有一套平衡补偿系统来改变主弹簧力的线性为恒定值。根据机械原理和理论力学，采用辅助弹簧来驱动四连杆机构，并配以曲线形轨道构成一套平衡补偿系统，补偿系统可以平衡主弹簧在拉伸过程中输出的拉力为一个恒定数值，实现恒力输出。图2所示为恒力系统学结构。

1.2.2 恒力系统的组成

恒力系统主要是由固定架、4根主弹簧K1、外载挂架、4根辅助弹簧K2、2条曲线轨道、拉杆、1套四连杆机构、4根主弹簧调整螺杆组成。其中，辅助弹K2、曲线轨道、拉杆、四连杆构成恒力系统中的平衡系统。

1.2.3 恒力系统中各部件的工作原理

固定架用于安装整个恒力系统；主弹簧K1直接与外负载挂架连接，其拉力直接作用于外负载；外负载挂架用于安装外载荷；4根辅助弹簧的拉力通过平衡系统中的四连杆、曲线轨道、拉杆组成的平衡系统平衡后输出平衡力至外负载挂架；2条曲线轨道提供四连杆铰接点的运行轨迹；拉杆负责输出辅助弹簧提供的平衡拉力；4根主弹簧调整螺杆用于调整主弹簧的预拉力，以配合外负载所需的拉力。

1.2.4 恒力系统各零部件的运行路径

图3所示为恒力系统各部件的运行情况。从图3中可以看出，当外载挂架开始向下方移动时，主弹簧开始伸长，同时，四连杆的铰接点A通过拉杆的牵引也开始随着外载挂架的移动而同步移动。四连杆机构通过4个铰接点将4根连杆组成一个封闭、对称的平行四边形。平行四边形铰接点A以及A的对角的铰接点受到辅助弹簧的拉力，铰接点B以及B的对角的铰接点向四边形外侧的曲线轨道驱动。这样，铰接点B以及对角的铰接点就可以沿着曲线轨道的下方移动，各部件按照移动的原则运动。

2 恒力系统的设计

2.1 系统的设计输入

2.1.1 结构尺寸要求

结构尺寸的要求为：产品安装面的尺寸为900 mm（长）×1 000 mm（高）×20 mm（厚）。

2.1.2 恒力输出范围

恒力输出范围为40～75 kgf。

2.1.3 工作行程

工作行程为0～650 mm。

2.2 恒力系统结构及原理图的设计

2.2.1 规划结构，制订外部尺寸要求

根据设计输入的尺寸要求进行结构的规划，制订外部安装尺寸要求，规划产品实现结构的最佳方案，布局各零部件，尽可能精确地排好主要的部件位置以及运动轨迹的范围。

2.2.2 划出输出恒力的范围，制订选择方案

初步划出输出恒力的范围，制订力学零件的选择方案与方向。

2.2.3 制订结构方案和运动轨迹方案

制订与工作行程相关的结构方案和运动轨迹的方案，尽可能配合补偿平衡系统所采用的主要零部件的尺寸以及工作要求。

2.2.4 具体设计

根据设计输入、草图及采用的原理确定结构尺寸。本文所阐述的主要是恒力系统，其主要零部件的尺寸需根据总装图确定。主弹簧采用外径小于或等于45 mm的圆柱拉伸弹簧，数量4根；辅助弹簧采用外径小于或等于25 mm的圆柱拉伸弹簧，数量4根；四连杆长度为400 mm，数量4根；曲线轨道2根。

3 恒力系统力学分析

根据工作原理及力学结构模型为系统建立等效的受力分析模型图，并对各部分部件进行受力分析，如图4所示。图4中，A，B，C，D为四连杆机构的4个铰接点。主弹簧K1为外载挂架提供弹力F1，辅助弹簧K2提供给四连杆铰接点C弹力F2。在四连杆机构中，上连杆受到来自铰接点的压力F3、F4、F5。F3、F4、F5为曲线轨道对连杆机构中铰接点的支撑力。P为系统向外载提供的拉力。连杆结构中铰接点A的位移量为h，铰接点C的位移量为l，轨道切线水平夹角为α，连杆与垂直线的夹角为β。根据设计要求，连杆的长度为400 mm，铰接点A与C的初始距离为750 mm，铰接点A的位移量为650 mm。图5所示为恒力平衡系统轨道曲线。

3.1 弹簧受力分析

3.1.1 主弹簧的受力分析

根据式（16）～（21），得到：

（-（200×（l/320 000-h/320 000+3/1 280））/（1-（l/800-h/800+15/16）^2）^（1/2）×dh/dl+（200×（l/320 000-h/320 000+3/1 280））/（1 -（l/800-h/800+15/16）^2）^（1/2））×（1 300×k1+k2×l-k1×h）×800×（1-（（750-h+l）/800）^2）^0.5/（k2×c+k1×h）/（750-h+l）+0.5×dh/dl+0.5=0. （24）

根据微分方程得到h与l之间的函数关系，整理式（22）得到：

（-（200×（l/320 000-h/320 000+3/1 280））/（1-（l/800-h/800+15/16）^2）^（1/2）×dh/dl+（200×（l/320 000-h/320 000+3/1 280））/（1-（l/800-h/800+15/16）^2）^（1/2））×（1 300×k1+k2×l-k1×h）×800×（1-（（750-h+l）/800）^2）^0.5/（k2×c+k1×h）/（750-h+l）+0.5×dh/dl+0.5=0. （25）

从结构模型图可以知道，定值a=400 mm，d=750 mm，从合力原理图可以看出Ft2是定值，Ft2的表达式为：

6 恒力系统部件的设计

6.1 设计弹簧

6.1.1 主弹簧设计

根据产品的设计输入和结构要求，主弹簧采用外径应小于或等于45 mm。结合恒力系统的合力分析图，考虑到系统在重力方向使用的工况，需要按照重力方向来设计主弹簧。由结构设计得到滑动部件的质量为18.1 kg，外负载受力为40～75 kg，则主弹簧的受力范围为58.1～93.1 kg（569.38～912.38 N）。由于属于II类载荷，极限载荷Pj=93.1×9.8×1.25=1140.5 N，采用4根弹簧，每根弹簧的极限载荷为Pj1=1140.5/4=285.2 N。

查《机械设计手册》，并根据Pj与D 得到每根弹簧的参数为：材料直径d=3.5 mm，弹簧中经D=40 mm，工作极限Pj=293.40 N，工作载荷下的单圈变形量f1=12.67 mm，单圈刚度Pd=23.2 N/mm，初拉力P0=22.1 N。

图6所示为主、辅弹簧对外载作用合力，弹性系数为kz，根据图6得到4×P0+4×kz×650=569.38，则每根主弹簧的弹性系数kz=0.185 N/mm，主弹簧的线径为-3.5 mm，中径为40 mm，有效圈数n=23.2/0.185=125.4，取n=126圈。

6.1.2 辅弹簧设计

依据主弹簧的弹性系数以及系统的工作行程得到辅助弹簧需要提供预拉力以及运行过程中的额外拉力，即预拉力Ft2=4×kz×650=481 N，系统运行工程中提供的额外拉力为1.25Ft2=601.25 N，辅弹簧受到的总拉力为 481+601.25=1 082.25 N，每根辅助弹簧的极限拉力为Pjf=1 082.25/4=270.6 N。

计算并查《机械设计手册》可得，辅弹簧的线径为3 mm，中径为20 mm，工作极限Pj=339.76 N，工作载荷下的单圈变形量f1=3.398 mm，单圈刚度Pd=100 N/mm，初拉力P0=47.7 N。

根据实际结构及弹簧变形量、单圈的刚度，取弹簧为100圈，即有效圈数n2=100，弹性系数kf=1 N/mm，初拉力为47.7 N。

6.2 轨道的设计

6.2.1 轨道曲线的建立

由式（12）（13）（25）得到轨道曲线方程为：

x=-400×（1-（（750-h+1/4/k2×（-13 00×k1+2×（422 500×k1^2+2 600×k2×k1×h-2×k2×k1×h^2）^（1/2）））/800）^2）^0.5+139.2. （28）

y=-（h+1/4/k2×（-1 300×k1+2×（422 500×k1^2+2 600×k2×k1×h-2×k2×k1×h^2）^（1/2）））/2. （29）

通过对弹簧的设计得出，看k1=4×kz=0.74 N/mm，k2=4×kf=4N/mm。

用Pro/ENGINEER在笛卡尔坐标系内绘制轨道曲线，则有：

x=-400×（1-（（750-650×t+1/4/4×（-1 300×0.74+2×（422 500×0.75^2+2 600×4×0.74×650×t-2×4×0.74×（650×t）^2）^（1/2）））/800）^2）^0.5+139.2. （30）

y=-（650×t+1/4/4×（-1 300×0.74+2×（422 500×0.74^2+2 600×4×0.74×650×t-2×4×0.74×（650×t）^2）^（1/2）））/2. （31）

z=0.

6.2.2 轨道结构设计

根据结构要求设计出轨道的厚度、宽度以及相关装配的结构。

6.3 其他附件的设计

根据设计规划设计相应的滑动机构、内部装配结构和外部安装结构。

7 恒力系统的设计验证

主要对弹簧进行设计验证。

7.1 校核恒力系统静载荷部件

对恒力系统静载荷部件进行强度校核。

7.2 运动模拟

进行运动模拟，检验运动过程中是否存在干涉现象。

7.3 校核安装部位的尺寸

对安装部位的尺寸进行校核。

7.4 主弹簧的设计验证

7.4.1 载荷验证

最大实际载荷Pnz=93.1×9.8/4=228.1 N，Pjz=228.1×1.25=285.2 N <293.4 N，合格。

7.4.2 不同行程状态下弹簧变形的验证

当最大外负载为75 kg时，主弹簧的受力为75+18.1（滑动部件自重）=93.1 kg×9.8=912.38 N。当外负载在行程为0时，主弹簧的长度为L0=（912-4×22.1-Ft2）/（4×kz）=462 mm，弹簧每圈变形量为f0=463/126=3.67 mm。当外负载在行程为650 mm时，主弹簧的长度为L1=L0+650=1 112 mm，弹簧每圈变形量为f1=L1/n=8.83 mm，其中，弹簧圈数n=126.

从以上得到，弹簧的单圈变形量最大为8.83 mm，小于标准单圈变形12.67 mm。主弹簧满足要求，辅弹簧验证合格。

8 恒力输出的调整

在恒力系统的恒力范围内调整主弹簧的调节螺杆。

9 结论

从轨道曲线方程可以得出，主、辅弹簧的弹性系数影响曲线轨道系统的输出，且恒力范围受到系统输出力方向和空间尺寸的限制。

参考文献

[1]成大先.机械设计手册[M].第四版.北京：化学工业出版社，2010.

[2]孙训方，方孝淑，观来泰.材料力学（1）[M].第五版.北京：高等教育出版社，2002.

[3]郑文维，吴克坚.机械原理[M].第七版.北京：高等教育出版社，2014.

[4]林清安.Pro/ENGINEER2001零件设计高级篇[M].北京：清华大学出版社，2003.

〔编辑：刘晓芳〕