基于三参数强度准则的煤矿立井井壁流固耦合理论分析

李雪梅，荣传新，程　桦

(安徽理工大学 土木建筑学院，安徽 淮南　232001)

基于三参数强度准则的煤矿立井井壁流固耦合理论分析

李雪梅，荣传新，程桦

(安徽理工大学 土木建筑学院，安徽 淮南232001)

摘要：将煤矿立井混凝土井壁视为多孔介质，考虑地下水渗流作用的影响，应用三参数强度准则和弹塑性力学理论，推导出了立井混凝土井壁弹性区和塑性区应力的解析表达式，以及井壁承受的地下水压力P0与塑性区半径rp之间的解析表达式。计算结果表明：当不考虑渗流作用时，井壁的极限承载力最大，井壁的环向压应力σθ是混凝土立方体单轴抗压强度的2.7倍左右；考虑渗流作用时，井壁所能承受的极限水压力Pc随混凝土孔隙率β增加而逐渐减小，当β=0.2时，井壁的环向压应力σθ是混凝土单轴抗压强度的2.4倍左右，故渗流作用对井壁应力分布影响很大；随着地下水压力的增大，处于弹性区的井壁混凝土径向压应力σr和环向压应力σθ逐渐增加，而当地下水压力增加，达到塑性半径所对应的极限荷载后，该位置的井壁混凝土径向和环向应力则保持不变。该成果为立井井壁结构设计提供了一定的理论参考。

关键词：煤矿立井井壁；三参数强度准则；弹塑性理论；流固耦合机理；地下水渗流

1研究背景

煤矿资源日益枯竭，迫使煤炭开发逐渐转向深部，新井建设时煤矿立井井筒需要穿过的冲积层越来越厚，为抵抗深厚冲积层巨大的外荷载作用，一个合理的途径就是尽可能地提高现行混凝土井壁结构的承载力，目前在井壁结构支护中均已采用高强混凝土。虽然高性能混凝土的使用解决了深井井筒支护的一些技术难题，但是由于冲积层厚度的加大，很多井筒常会发生突水和涌水事故，严重威胁着矿井的安全生产和矿下作业人员的生命安全。如2010年2月18日潘三矿西风井突发井筒出水事故, 井筒出水量约300m3/h；又如因井筒突水险些造成淹井事故的淮南矿业集团顾桥煤矿副井；还有张北煤矿的3个井筒、国投新集刘庄煤矿的4个井筒等，都曾出现较大的突水事故。

有关混凝土井壁结构的力学特性研究，许多学者已做出了很大的贡献[1-5]，但是这些研究者均把混凝土井壁视为弹性体和理想弹塑性体，而混凝土是一种非线性介质，弹性理论只适用于其受力和变形的初期。在考虑渗流作用的情况下，荣传新等[6]采用统一强度理论对井壁结构流固耦合机理做了分析研究。为了进一步分析地下水渗流作用对矿井井壁稳定性的影响，文献[7]根据前人研究成果将井壁混凝土视为一种可变的多孔介质材料，采用更加符合混凝土强度特性的三参数强度准则[8-9]对煤矿立井井壁流固耦合机理进行了理论分析。

图1　地下水压力作用下混凝土井壁力学模型Fig.1　Mechanical model of concrete shaft lining under hydraulic pressure

2三参数准则下混凝土立井井壁渗流作用解析解

如图1所示，取井筒轴

线为z轴建立柱坐标系，取井壁内半径为a，外半径为b，地下水压力为P0。

假设混凝土为多孔介质，孔隙率为β，渗透系数为k，弹性模量为E，泊松比为μ。主应力符号规定，拉为“+”、压为“-”，且σ1>σ2>σ3。

假设混凝土立井井壁为平面应变问题，井壁混凝土均匀、各向同性，屈服前为完全弹性，屈服后符合三参数强度准则。三参数强度准则中考虑了混凝土受多轴应力[10]的影响，使其更符合井壁混凝土一般处于双向或三向应力状态的实际情况。据文献[6]中的弹性解，得混凝土井壁弹性区应力分布为：

(1)

(2)

注：图2(b)中O，N两点重合。图2　混凝土三参数强度准则屈服面Fig.2　Yield surface of three-parameter strengthcriterion of concrete

(3)

混凝土三参数强度准则的屈服面如图2所示。

(4)

式中：

其中:Ky=σy/σl;K2y=σ2y/σl;σy为单轴抗压强度；σ2y为双轴抗压强度;σl为单轴抗拉强度。

在塑性区(a≤r≤rp)内，将应力分量以ξ和ρ表示，由式(3)的第1、第2式得：

(5)

平衡方程为

(6)

将式(5)代入式(6)整理得

(7)

由式(4)得

(8)

将式(8)代入式(7)整理得

(9)

将式(9)积分，并利用边界条件σr|r=a=0，整理可得

(10)

因此，

(11)

(12)

将式(10)变形整理可得

(13)

式(13)具有与式(12)相同的形式，记

应用LamnertW函数的W-1(x)分支，将x的表达式代入W(x)，整理后得到

(14)

(15)

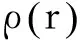
混凝土井壁弹性区一侧，当r=rp时，将式(1)、式(2)代入方程组(3)的第1式得

(16)

式(16)中q和rp均未知，可以由弹性与塑性交界处径向应力相等的条件确定它们之间的关系。在塑性区r=rp处求σr时，利用式(5)第1式和式(8)，则有

(17)

将式(17)代入式(16)整理得

由此解得

(18)

混凝土井壁塑性区一侧，当r=rp时，由式(14)有

(19)

由弹性区和塑性区交界面处的连续性条件，将式(18)、式(19)联立，并将参数值代入并利用MATLAB求解可得地下水压力P0与塑性区半径rp关系。

3矿井井壁流固耦合机理分析

3.1地下水的渗流作用对井壁极限承载力的影响

计算绘出井壁混凝土孔隙率β与井壁所承受的地下水压力P0和塑性区半径rp的关系曲线如图3所示，β取不同值时，井壁所能承受的地下水压力P0的变化如表1所示。由图3和表1可见，在不考虑渗流作用时井壁的极限承载力最大为22.81MPa；考虑渗流作用时，井壁所能承受的极限水压力Pc随混凝土的孔隙率β增加而逐渐减小；由此可见，地下水的渗流作用对井壁的极限承载力影响很大。

3.2井壁应力与地下水压力之间的关系

当井壁混凝土的孔隙率β=0.2，井壁塑性区半径rp=4.0m时，井壁能承受的地下水压力为9.35MPa(井壁完全处于弹性区)；rp=4.5m时，地下水压力为15.52MPa；rp=5.0m时，地下水压力为17.55MPa(井壁完全处于塑性区)。在这3种荷载作用下，井壁外围应力σr，σθ和半径r的关系曲线如图4所示。

图3　不同β下的地下水压力P0与塑性区半径rp的关系曲线Fig.3　Curves of hydraulic pressure P0 vs. plastic radius rp under different values of porosity β

孔隙率β井壁所能承受的极限水压力Pc/MPa022.810.119.860.217.550.315.70

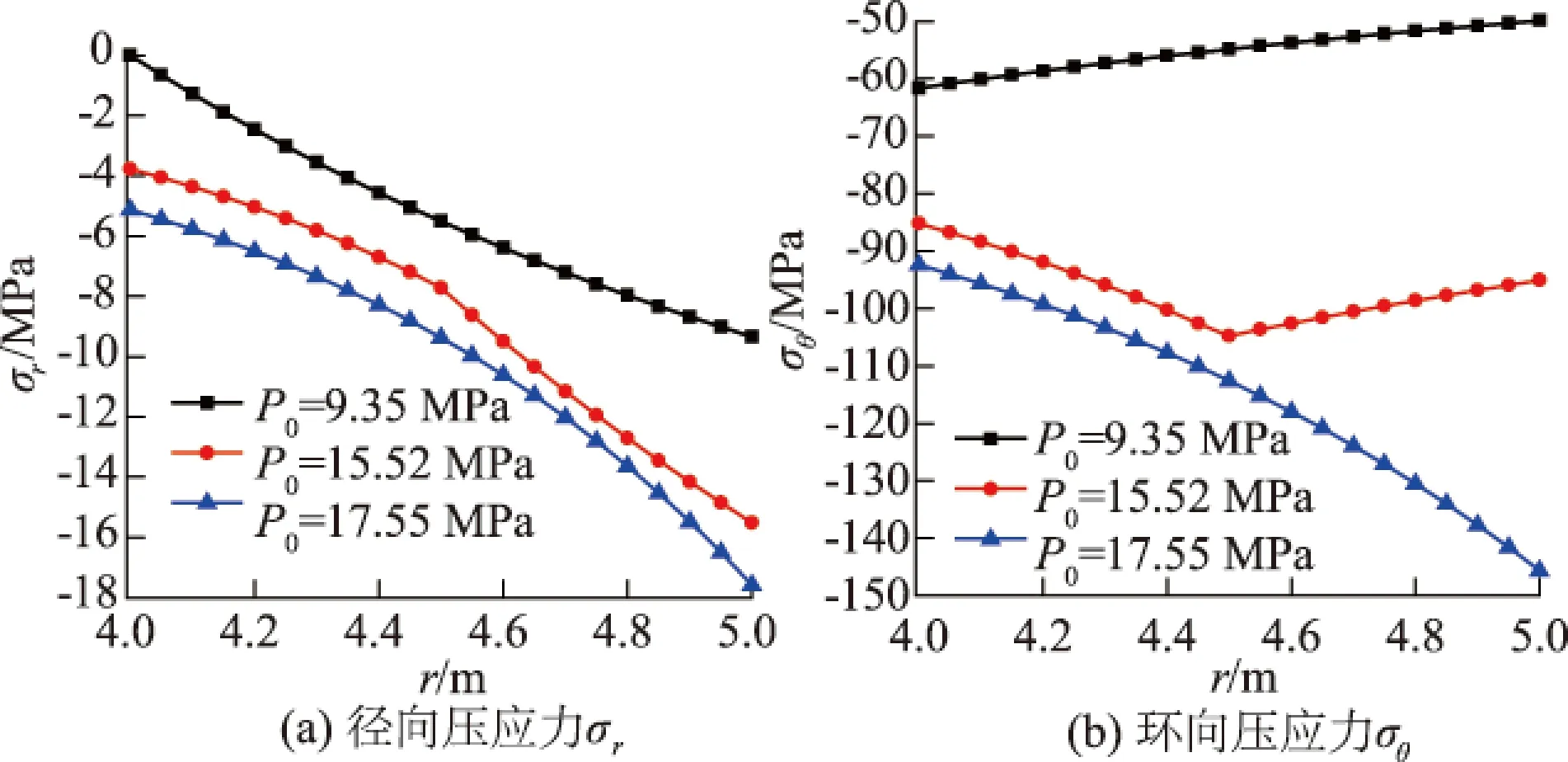
图4　β=0.2时，不同地下水压力P0处的压应力与半径r的关系曲线Fig.4　Curves of compressive stress vs. radius runder different hydraulic pressures, when β=0.2

由图4可见，在弹性区，径向压应力σr随半径r的增大而增大，而环向压应力σθ随半径r的增大而减少；在塑性区，径向压应力σr和环向压应力σθ均随半径r的增大而增大。

图5　β=0时，不同地下水压力P0处的压应力与半径r的关系曲线Fig.5　Curves of compressive stress vs. radius r under different hydraulic pressures P0when β=0

当井壁所受地下水压力等于17.55MPa(塑性极限承载力)时，由于考虑了混凝土多轴强度的影响，井壁的环向压应力σθ达到145.63MPa，是混凝土立方体单轴抗压强度的2.4倍左右。当井壁混凝土的孔隙率β=0时，如图5可见，弹性区和塑性区压应力的变化趋势与β=0.2时相同，而当井壁所受地下水压力等于22.81MPa(塑性极限承载力)时，井壁的环向压应力σθ达到164.20MPa，是混凝土立方体单轴抗压强度的2.7倍左右，故渗流作用对井壁应力分布影响很大。

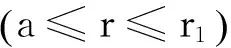
图6　β=0.2时，不同位置处压应力σr,σθ与地下水压力P0的关系曲线Fig.6　Curves of compressive stress vs. hydraulic pressure P0 at different positions when β=0.2

4结论

(1) 地下水的渗流作用对井壁的极限承载力影响很大，不考虑渗流作用时井壁极限承载力最大，而考虑渗流作用时，井壁所能承受的极限水压力Pc随混凝土的孔隙率β增加而逐渐减小。

(2) 在地下水压力作用下，弹性区，径向压应力σr随半径r的增大而增大，而环向压应力σθ随半径r的增大而减少；在塑性区，径向压应力σr和环向压应力σθ均随半径r的增大而增大。当混凝土井壁承受的地下水压力达到其塑性极限承载力时，由于考虑了混凝土多轴强度的影响，在考虑地下水渗透(β=0.2)影响时，井壁的环向应力σθ是混凝土单轴抗压强度的2.4倍左右；当不考虑地下水渗透(β=0)影响时，井壁环向压应力是混凝土立方体单轴抗压强度的2.7倍左右，故渗流作用对井壁应力分布影响很大。

(3) 随着地下水压力的增大，处于弹性区的井壁混凝土径向压应力σr和环向压应力σθ逐渐增加，而当地下水压力增加达到塑性半径所对应的极限荷载后，该位置的井壁混凝土径向和环向应力则保持不变，表明井壁混凝土塑性区应力仅和塑性区半径和混凝土本身的性能有关。

参考文献：

[1]姚直书，程桦，荣传新. 深冻结井筒内层钢板高强钢筋混凝土复合井壁实验研究[J]. 岩石力学与工程学报, 2008, 27 (1):153-158.

[2]程桦, 孙文若, 姚直书. 高强混凝土井壁模型实验研究[J]. 建井技术，1995,16(6): 26-27.

[3]姚直书，程桦，孙文若. 深厚表土层中高强复合井壁结构的试验研究[J]. 岩土力学, 2003, 24 (5):739-743.

[4]姚直书，程桦，杨俊杰. 深表土中高强钢筋混凝土井壁力学性能的试验研究[J]. 煤炭学报，2004，29(2)：167-171.

[5]杨俊杰.混凝土结构井壁的破坏特征和强度特征[J]. 煤炭学报，1998, 23(3):246-251.

[6]荣传新，王秀喜，蔡海兵,等. 基于流固耦合理论的煤矿立井井壁突水机理分析[J]. 煤炭学报, 2011, 36(12):2012-2108.

[7]梁通，金 峰. 基于广义有效应力原理的混凝土坝分析[J]. 水力发电学报, 2009, 28(2): 47-51．

[8]李朝弟. 结构的安定性与极限分析[D]. 北京: 清华大学工程力学系, 1991.

[9]徐秉业，刘信声.应用弹塑性力学[M].北京:清华大学出版社，1995.

[10]过镇海，王传志. 多轴应力下混凝土的强度破坏和破坏准则研究[J]. 土木工程学报，1991,24(3): 1-13.

[11]HWANGC,CHENGYC.ANoteontheUseoftheLambertWFunctionSubjecttoaLargeDelayinaLaserSystem[J].Automatica, 2005, 41: 1979-1985.

[12]李俊余，王在华. 一类时滞系统Hurwitz稳定的简单判据[J]. 动力学与控制学报，2009,7(2): 136-142.

[13]GB50010—2010,混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2010.

[14]KUPFERH,SHINOZUKAM,SCHUELLERG.BehaviorofConcreteunderBiaxialStress[J].AmericanConcreteInstitute, 1969, 66(8): 656-666.

(编辑：刘运飞)

Analysis of Coal Mine Shaft Lining with Fluid-solid CouplingTheory Based on Three-parameter Strength Criterion

LIXue-mei,RONGChuan-xin,CHENGHua

(SchoolofCivilEngineeringandArchitecture,AnhuiUniversityofScienceandTechnology,Huainan232001,China)

Abstract:As porous medium, concretes of the shaft lining of coal mine are affected by underground water seepage flow. The three-parameter strength criterion and elastic-plastic theory are used to obtain the stress distribution of shaft lining in the elastic zone and plastic zone, and the analytical expression between the groundwater pressure P0 on shaft lining and the plastic zone radius rp. The results show that the ultimate bearing capacity of the shaft lining is the largest when seepage flow is not considered, and the hoop stress σθof the shaft lining is about 2.7 times of the uniaxial compressive strength of concrete cubes. However, when seepage flow is considered, the ultimate hydraulic pressure that the shaft lining can bear gradually decreases with the increases of porosity β, and when β equals 0.2, the hoop stress of the shaft lining is about 2.4 times of the uniaxial compressive strength of concrete cubes. Therefore, seepage flow has significant influence on the stress distribution of the shaft lining. Moreover, with the increase of hydraulic pressure, the radial stress σr and the hoop stress σθof concrete in the elastic zone gradually increase, however, when the hydraulic pressure reaches or exceeds the limit pressure(corresponding to the plastic radius), the radial stress σr and the hoop stress σθin this position remains unchanged. The results provide theoretical reference for the structure design of shaft lining.

Key words:shaft lining of coal mine; three-parameter strength criterion; elastic-plastic theory; fluid-solid coupling mechanism; groundwater seepage flow

收稿日期：2015-07-20；修回日期：2015-09-25

基金项目：国家自然科学基金项目(51374010，51474004)；安徽高校省级自然科学研究重点项目(KJ2010A094，KJ2011A093)

作者简介：李雪梅(1986-)，女，安徽亳州人，硕士研究生，主要从事岩土工程结构方面的研究，(电话)13866312175(电子信箱)1028655694@qq.com。 通讯作者：荣传新(1968-)，男，安徽六安人，教授，博士生导师，主要从事岩土工程和结构工程方面的教学与科研工作，(电话)0554-6633833(电子信箱)chxrong@aust.edu.cn。

doi:10.11988/ckyyb.20150610

中图分类号：TD32

文献标志码：A

文章编号：1001-5485(2016)06-0083-05

2016,33(06):83-87，93