内模控制在温度控制传感器系统中的应用*

常　峰，旷文珍，陆　帅

(兰州交通大学 光电技术与智能控制教育部重点实验室，甘肃 兰州 730070)

内模控制在温度控制传感器系统中的应用*

常峰，旷文珍，陆帅

(兰州交通大学 光电技术与智能控制教育部重点实验室，甘肃 兰州 730070)

摘要:为了适应现实状况对于提高控制效果的要求，对温度控制传感器系统采用了内模控制方法，完成基于内模控制的温度控制系统设计。针对具有大时滞的温度控制对象完成基于内模控制的温度控制系统设计；对相同的大时滞温度控制对象，完成基于PID控制的温度控制系统设计，并在Matlab/Simulink仿真平台上对所设计的温度控制系统进行仿真分析。仿真结果表明了内模控制滤波器的时间常数对系统控制效果的影响规律，其控制效果优越于PID控制。

关键词:温度控制；内模控制；大时滞；PID控制

0引言

目前，温度已成为工业中经常遇到的一种控制对象，在冶金、化工、机械等各类工业中，广泛使用各种电阻炉、热处理炉、过热蒸汽炉等温度控制系统。所以，在工业领域的许多重大技术经济指标直接受温度控制效果的影响，如，生产安全、生产效率的提高、产品质量的保证、节约资源等指标。

在温度控制系统发展中应用PID控制[1]、施密斯预估控制[2]、达林控制[3]等控制方法，但是由于温度控制系统的非线性、大时滞、特性参数随温度变化及强耦合特性等特点[4]，使得以上控制方法不能够获得较高要求的控制效果，且在实现过程中控制算法相对比较复杂。因此，经过长期实践经验的累积，人们根据工业过程的控制规律，提出了内模控制策略。

内模控制主要的优势,一是响应速度快，即使模型不准确仍然具有较大优势；二是具有较强的鲁棒性，内模控制的结构特点使其对过程中的不确定性有很好的适应性，从而使控制系统的稳定性得到很好的保证。而且内模控制器的设计比较简单、控制性能好、便于系统分析、对于数学理论的要求不高、应用时计算量小，易于为广大工程人员所接受[5]。

1内模控制

内模控制的基本思路是将内部模型和实际控制对象做成并联的结构，控制器取模型的动态逆，在鲁棒性和输入约束不被考虑的条件下，使闭环系统的性能可以得到满足，通过低通滤波器的添加提高系统的鲁棒性，从而使其能够对外界干扰和模型失配带来的不利影响有一定的适应性[6]。

1.1内模控制基本原理[7,8]

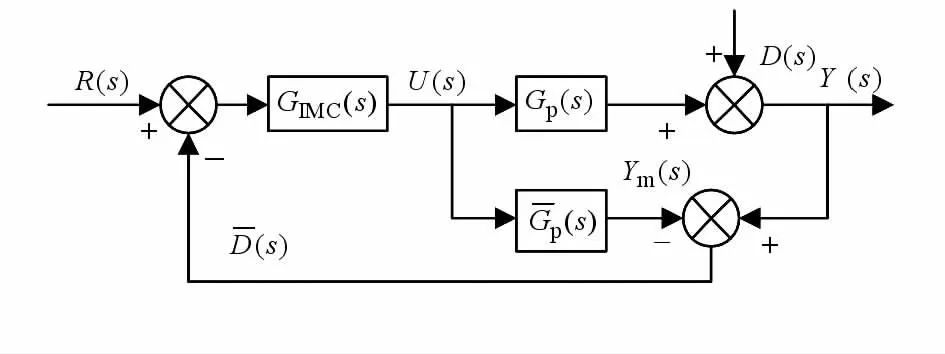
图1　内模控制结构框图Fig 1　Structure diagram of internal model control

对于内模控制的设计思路应先从理想控制器出发，进而考虑实际存在的约束条件，设计出符合实际要求的控制器[9,10]。图1中，系统存在两个输入：扰动信号输入(假定为不可测)D(s)和输入给定值R(s)。下面分别讨论在对系统分别施加两种不同输入时系统的输出情况。

由于假定此时R(s)=0，故根据图1可得

Y(s)=D(s)[1-GIMC(s)Gp(s)]

(1)

(2)

将式(2)代入式(1)可得

Y(s)=0

(3)

由式(3)可以得出结论：当R(s)=0，D(s)≠0，以及模型准确且可倒的情况下，本控制器是可以对外界扰动有很好抑制的理想控制器。

Y(s)=GIMC(s)Gp(s)R(s)

(4)

式(4)表明：在R(s)≠0，D(s)=0，以及模型准确且可倒时，本控制器是Y(s)能对R(s)的变化进行跟踪的理想控制器。

由图1可得，内模控制存在以下关系式

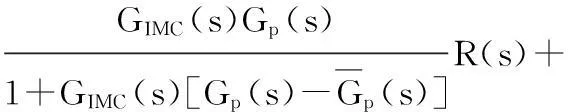
(5)

如果模型准确时，式(5)可以化简为

Y(s)=GIMC(s)Gp(s)R(s)+[1-GIMC(s)Gp(s)]D(s)

(6)

其中,反馈信号为

(7)

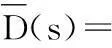
1.2内模控制在温度控制传感器系统中的应用

1)温度控制传感器的数学建模

在对温度控制系统进行分析与设计中，首先要建立温度控制对象的数学模型，选取的温度控制对象是经常见到的电加热炉。从控制的角度分析，因为电加热炉温度控制具有升温单向性、惯性、大滞后和时变性的特点[11]。对其控制难度也有所增加，且其升温单向性又是必须面对的问题。升温单向性是因为电加热炉是依靠电加热对工件进行升温保温；但其降温是自然冷却。当温度超调，就无法使用有效的控制手段对其进行降温。由于以上的原因存在，所以,电加热炉难以用数学模型精确进行表达。通常其数学模型可以用以下模型定性描述

(8)

式中X为电加热炉内温升(炉内温度与室温温差)，K为放大系数，τ0为纯滞后时间，t为加热时间，T为时间系数，V为控制电压。

对式(8)进行拉氏变换整理后，得到

(9)

2)对过程模型进行因式分解

(10)

3)控制器设计

(11)

因为输入为阶跃信号，故可以确定内模控制滤波器的形式为

(12)

式中参数r的选取必须可以使GIMC(s)成为有理的传递函数。由式(11)与式(12)可知,取r=1即可满足要求。

4)模型参数的选取

模型参数取为K=1.6，τ=80，T=120。因为τ/T=80/120≥0.5,满足大时滞系统的定义，本次所选的温度控制对象是一个具有大时滞特性的控制对象。要求将温度控制在30°，误差小于5 %。内模控制的温度控制系统结构图可表示为如图2所示。

图2　内模控制的温度控制系统结构图Fig 2　Temperature control system structure diagram of internal model control

图2是在模型准确的条件下进行设计的，所以,过程模型与控制对象的数学模型相同。其中，D(s)是不可预测的外界干扰，而Tf的值是不确定的，可以对其进行调整。

2温控系统中影响内模控制的因素

2.1扰动对系统的影响

在模型准确且Tf没有变化的情况下，仍以式(9)所描述的数学模型为对象，给定输入阶跃信号R(s)=30，对系统在无扰动和在控制器输出端加入20 %阶跃扰动信号下进行仿真，分析输出波形。利用Matlab/Simulink仿真平台，在上述条件下搭建系统的仿真框图，选取Tf=10进行仿真，观察系统输出波形如图3所示。

图3　Tf=10时的输出波形Fig 3　Output waveform of Tf=10

由图3可知，在无扰动时系统的响应速度很快，系统很快进入稳定状态。而存在扰动时，系统会产生超调量，经过较长的调整时间后才能进入稳定状态。因此,当系统存在扰动时会对系统的控制效果产生不利影响。

2.2温控对象模型失配时对系统的影响

在控制器没有发生变化但是被控对象模型失配的情况下，对系统加上相同阶跃输入信号R(s)=30且无扰动信号时进行仿真，通过改变被控对象模型的参数使过程增益为1.8、时间常数为110，此时被控对象模型处于失配状态下，得到仿真输出波形如图4所示。

图4　模型失配时的输出波形Fig 4　Output waveform of model mismatch

由图3与图4的对比可知，系统在被控对象模型准确时响应速度很快，可以很快进入稳定状态。而在系统被控对象模型发生变化时，系统会产生超调量且有振荡现象发生，需要经过较长调整时间后才进入稳定状态。故当被控对象模型失配时会对系统的控制效果产生不利影响。

2.3内模滤波器时间常数对系统的影响

外界扰动和被控对象模型失配均会对系统的控制效果产生不利影响,但是外界扰动与被控对象模型失配现象却是客观的存在，不能进行自主调整,而内模滤波器时间常数是可以自主进行调整的参数。

1)过程无扰动时，在图3的基础上通过改变Tf值的大小可获得不同Tf值时的系统仿真框图，取Tf值分别为1,5,15,18时，仿真得到输出波形如图5所示。

图5　无扰动时Tf变化的输出波形Fig 5　Output waveform of Tf changes without disturbance

从图5可看出Tf的取值越小，系统的响应速度会越快;反之,Tf的取值越大，则系统的响应速度越慢。所以,Tf的取值对系统的响应速度有影响，如果对系统的响应速度进行考虑，则对于Tf值的选取应该越小越好。

2)在控制器输出端加入20 %阶跃扰动信号扰动时，取Tf值分别为10,20,30,100时，进行仿真，得到输出波形如图6所示。

图6　有扰动时Tf变化的仿真波形Fig 6　Simulation waveform of Tf changes with disturbance

3)通过分析可知，对于Tf值的选取，不能太大也不能太小，Tf选取的太大不能兼顾系统的响应速度；同理,如果Tf值选取太小又不能兼顾系统的鲁棒性。所以,在进行Tf值的选取时，既需要考虑系统的响应速度同时也要周全系统的鲁棒性。

当被控对象不变时，在系统无扰动和在控制器输出端加20 %扰动信号的情况下，输入给定信号R(s)=30时。在Matlab/Simulink仿真平台中进行调试，比对不同Tf值时的控制效果。最终选取Tf=40时内模控制的温度控制系统，其仿真框图如图7所示。

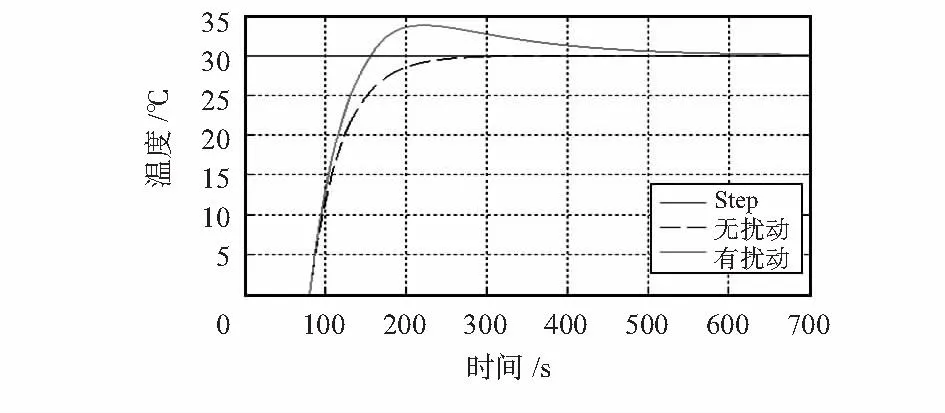
图7　Tf=40时的输出波形Fig 7　Output waveform of Tf=40

当Tf=40时，系统的控制效果比较理想，对于响应速度与鲁棒性两者均可以兼顾得到，不会过分偏重于某一方面。

3内模控制与PID控制效果比较

1)过程无扰动时控制效果的比较。当控制对象不变，系统没有扰动且输入阶跃信号为R(s)=30时，对内模控制与PID控制均在最佳状态下的温度控制系统进行仿真分析，探讨内模控制与PID控制的优越性，输出波形如图8所示。

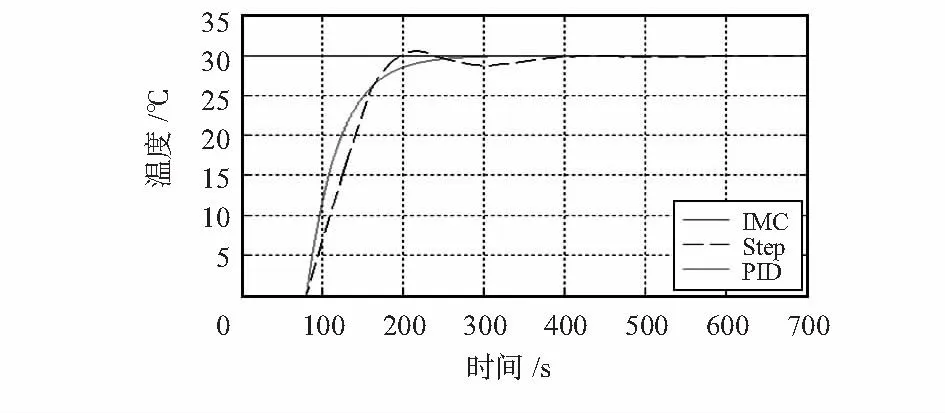
图8　内模与PID控制在无扰动时输出波形Fig 8　Internal model and PID control output waveform without disturbance

内模控制的响应速度比PID控制较快，且系统不会有超调现象出现，可以很快进入稳定状态。而PID控制时系统则有一定的超调量出现，并需要一定的调节时间，最后才慢慢趋于稳定，在系统没有扰动的情况下，内模控制比PID控制效果更为理想。

2)过程有扰动时控制效果的比较。当控制对象不变，系统输入阶跃信号为R(s)=30时，在控制器输出端加20 %扰动信号探讨内模控制与PID控制的优越性，在仿真平台上搭建仿真框图，输出波形如图9所示。

图9　内模与PID控制在有扰动时仿真波形Fig 9　Simulation waveforms of internal model and PID control with disturbance

可以看出,在系统存在扰动的情况下，虽然两种控制都存在超调量，但内模控制的系统超调量比较小，且调节时间比较小，而PID控制的超调量相对较大，且其调节时间相对较长。从图9的仿真波形中还可以看出，内模控制的响应速度依旧比PID控制快，在系统存在扰动时内模控制依旧比PID控制的效果理想。

4结论

当系统存在扰动和被控对象模型失配时会对系统的控制效果产生不利影响；内模控制滤波器的时间常数对内模控制的响应速度与鲁棒性均有着直接影响，当内模控制滤波器时间常数越大，系统的鲁棒性越强；反之，系统的响应速度越快。通过对PID控制与内模控制的温度控制系统进行性能比较分析，结果表明：PID控制对大时滞特性的温度控制对象的控制效果不如内模控制，内模控制在响应速度与鲁棒性方面均优越于PID控制。内模控制器的设计简单、易于实现，且对大时滞特性的温度控制对象的控制效果非常好。

参考文献:

[1]王伟,张晶涛,柴天佑.PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.

[2]赵东亚,邹涛,王治平.Smith 预估控制研究进展[J].化工进展,2010,29(8):1406-1409.

[3]杨琳娟,李秋明,顾德英.大林算法在炉温控制中的应用[J].仪器仪表学报,2005,26(8):2253-2254.

[4]Sun Zhaoping,Chen Juan,Zhu Xiangting.Multi-model internal model control applied in temperature reduction system[C]∥2014 11th World Congress on Intelligent Control and Automation(WCICA),IEEE,2014:247-250.

[5]戴文战,丁良,杨爱萍.内模控制研究发展[J].控制工程,2011,18(4):487-495.

[6]高金源,夏洁.计算机控制系统[M].北京:清华大学出版社,2007:215-234.

[7]王佳伟,杨亚非,钱玉恒.基于内模控制的工业控制系统仿真器鲁棒PID控制器设计[J].实验室技术与管理,2015,32(1):120-123.

[8]王树清.先进控制技术及应用[M].北京:化学工业出版社,2001:184-213.

[9]杜文嫚,韩璞.锅炉主蒸汽温度控制系统预测控制设计与仿真[J].计算机仿真,2013,30(7):392-395.

[10] Alberto Isidori,Lorenzo Marconi,Laurent Praly.Robust design of nonlinear internal models without adaptation[J].Automatica,2012,48(10):2409-2419.

[11] 杨大勇,李鸣.内模控制在电加热炉温度控制中的应用[J].微计算机信息,2008,24(10):42-43.

Application of internal model control in temperature control sensor system*

CHANG Feng，KUANG Wen-zhen，LU Shuai

(Key Laboratory of Opto-Technology and Intelligent Control,Ministry of Education，Lanzhou Jiaotong University，Lanzhou 730070,China)

Abstract:In order to adapt to requirement of reality for improving control effect,internal model control method is used in temperature control sensor system,complete design of temperature control system based on internal model control.Aiming at temperature control object with large delay,complete temperature control system design based on internal model control;for same large time-delay temperature control object,complete design of temperature control system based on PID control,and the designed temperature control system is simulated and analyzed on Matlab/Simulink simulation platform.Simulation result show that control effect of time constant of internal model control filter on system are studied,and internal model control effect is verified,superior to that of PID control.

Key words:temperature control;internal model control;large delay;PID control

DOI:10.13873/J.1000—9787(2016)05—0149—05

收稿日期：2015—08—30

*基金项目：甘肃省青年科技基金资助项目(1308RJYA096，145RJYA251)；甘肃省高校科研项目(2013A—050)

中图分类号:TP 23

文献标识码:A

文章编号:1000—9787(2016)05—0149—05

作者简介:

常峰(1989-)，男，甘肃兰州人，硕士研究生，主要研究方向为交通信息工程与控制。