基于压缩感知的虚拟暗室测试方法
2016-06-24章耀文陈少昌
章耀文, 陈少昌
(海军工程大学 电子工程学院,湖北 武汉 430000)
基于压缩感知的虚拟暗室测试方法
章耀文, 陈少昌
(海军工程大学 电子工程学院,湖北 武汉 430000)
摘要:为了在现场电磁发射测试中有效滤除背景噪声,针对存在相关信号的环境中多重信号分类(MUSIC)算法失效的问题,提出基于压缩感知(CS)的虚拟暗室测试方法。通过CS理论获得受试设备的辐射信号和环境中其他干扰信号的来波方向,并采取最小方差无畸变波束形成算法进行波束形成,从而对干扰信号实现有效抑制。该方法不仅适用于存在相干信号的情况下,而且不受阵列结构限制,应用更加灵活。通过仿真验证:方法在保证受试设备特性不失真的情况下能够有效抑制干扰噪声。
关键词:虚拟暗室; 压缩感知; 波束形成
0引言
对于大型系统或已固定设备的电磁干扰(electromagneticinterference,EMI)问题,因为屏蔽室容量有限或设备已经固定,EMI测试无法在屏蔽室内完成,需要采用现场测试来进行EMI测试。但是,普通环境中的背景噪声会超出电磁兼容(electromagneticcompatibility,EMC)的极限值,并且被测设备(equipmentundertest,EUT)产生的电磁信号可能会被环境中的背景噪声所调制。所以,想在普通环境下进行测试就必须设法消除背景噪声的影响。针对以上难题,MarinoJr和MichaelA于2002年提出虚拟暗室测试理论,并于2005年申请和获得了虚拟暗室的专利[1]。该理论自适应噪声抵消技术,使用双通道分布测试克服单通道测试带来的时间差问题。基于虚拟暗室理论设计的CASSPER系统被美国军方采购和使用。FrenchA和BraunS等人还提出了基于时域自适应噪声抵消的电磁辐射发射现场测试方法[2]。但这些基于自适应噪声抵消的虚拟暗室技术要求测试环境中不能有与EUT同频的信号分量以及参考通道中不能存在EUT信号等。DmochowskiJP提出基于波束形成的干扰抵消技术[3],不需要参考通道并且具有很好的干扰抑制效果。卢中昊和林铭团等人提出了基于阵列信号的虚拟暗室技术[4],通过实验证明方法的可行性。但文中采用的算法只能用于独立信号并且受到阵列结构限制,使得应用条件受到限制。
当EUT放置在室内环境,如舱室环境中,EUT信号和背景电磁噪声在空间中不断地发生反射、散射。由于空间相对狭小,反射后的强度并没有减弱多少,会产生相干信号。同时,由于实际的测量环境中,阵列的排布方式往往是受实际尺寸限制的,而绝大多数实际条件不能够满足均匀阵布阵要求[5,6]。针对以上情况,本文根据空域滤波原理,引入压缩感知(compressivesensing,CS)理论和波束成形技术,实现环境干扰的滤除,既可以有效处理相干信号,并且可以使用于任意阵列。
1基本原理
如图1所示,在EUT周围设置天线阵列,每个天线单元均可以接收到由EUT辐射信号和背景干扰信号所组成的混合信号,这个混合过程与各辐射源到天线的电磁传播路径有关,利用基于CS理论的空间谱估计技术获取各个信号的波达方向(directionofarrival,DOA)。根据信号的空间谱估计结果对各阵列接收信号做最优加权,在保证EUT辐射信号不失真的前提下,使阵列波束在干扰信号的来向形成“零陷”,实现对信号的空域滤波,进而来准确反映出EUT的真实辐射信号特性。
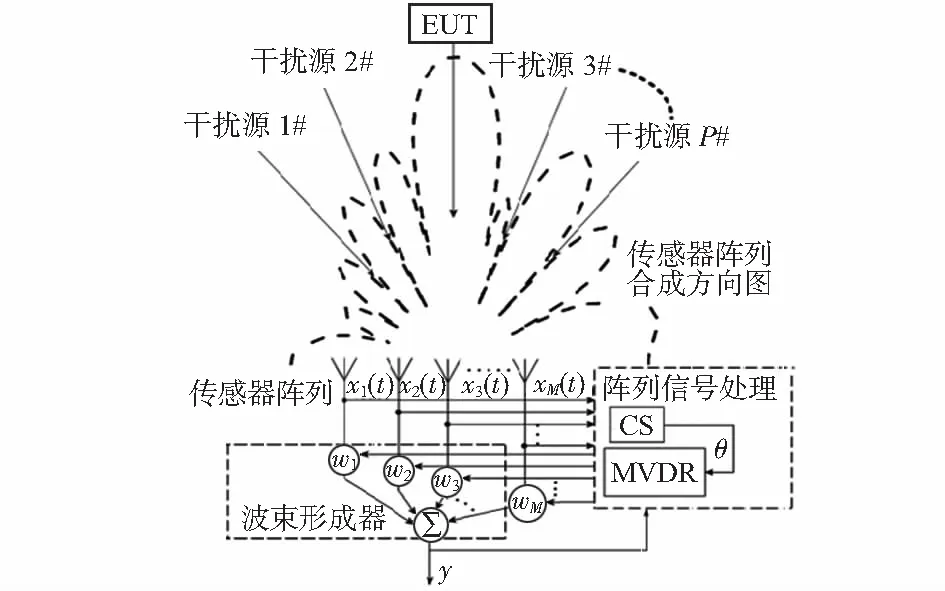
图1 基于空域滤波的电磁辐射发射现场测试体系Fig 1 Emission field of electromagnetic radiation testing system based on spatial filtering
2基于CS的DOA估计
CS[7]理论表明:当信号具有稀疏性或可压缩性时,通过采集少量的信号投影值就可以实现信号的准确或近似重构[8]。
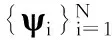
(1)
式中S仅含有K个(K≪N)个非零值,此时称信号X是可压缩的。利用M×N(M≪N)维观测矩阵Φ对可压缩信号进行观测,其表达式为
Y=ΦX=ΦΨZ=ΘS
(2)
式中Φ∈RM×N为测量矩阵,Ψ∈RN×N为信号的稀疏表示基矩阵。S∈RN×1为稀疏表示系数,y∈RM×1为测量向量,Θ∈RM×N为由测量矩阵和稀疏表示基矩阵构成的字典,也称之为信息算子。由CS理论可知,如果Θ满足有限等距性(restricted isometry property,RIP)等稀疏重构条件,则可以求解以下L0范数为题和极高的概率精准重构系数信号S。
假设有K个远场窄带信号入射到有M个的任意平面天线的阵列上,第k个信号的入射角度为θk。入射信号的波长为λ。t时刻阵列接收的快拍数据矢量可以表示为
X(t)=A(θ)S(t)+N(t),t∈{1,2,…,T}
(3)
式中X=[x(1),…,x(T)]T,N=[n(1),…,n(T)]T,A为M×K维的阵列导向矢量矩阵,表达式为
A=[a(θ1)a(θ2) …a(θK)]
(4)
a(θi)=[e-jωτ1i,e-jωτ2i,…,e-jωτMi]T
(5)
式中ω为入射信号的中心频率,τli为第i个信号在第l个阵列位置相对参考阵元的延时(波程差),且ωτli=2π(dxlcosθl+dylsinθi)/λ,(dxl,dyl)为第l个阵元的位置坐标。
辐射信号的潜在方位按照等角度空间划分方法,分成均匀的网格,抽样网格数量为n,设第i个潜在信号信号的入射角度为θi,且θi∈[-π,π],则网格索引为{θ1,θ2,…,θn},假定每个方位都对应潜在的信号si(i=1,2,…,p),构造出一个n×1维的信号S=[s1,s2,…,sn],显然S中只有k个位置有非零的元素,其余n-k的位置均为零,由于潜在信源个数远远大于实际信源个数,因此,信号S是稀疏的[9]。
针对公式的求解可以采用MOMP算法、MORMP算法、MFOCUSS算法和RMFOCUSS算法等,文献[10]对上述集中算法做了分析比较,在同等条件下RMFOCUSS算法比较其他算法恢复成功率高且误差小。
本文采用RMFOUSS算法实现稀疏信号的恢复和重构[11],其算法如下
Wk+1=diag(ck[i]1-p/2)
(6)
其中
(7)
(8)
其中
(9)
其中,p的选取与信号稀疏度有关,p越小表示信号越稀疏,λ为反映噪声功率大小的变量,通过调节参数λ可以除去部分噪声。当噪声服从标准正太分布时,则有λ=σ2,其中,σ2为噪声的方差。
通过RMFOCUSS算法可以求出谱估计公式为
P(θi)=‖S(i,:)‖2,i=1,2,…,L
(10)
3阵列波束控制与零点形成
适应波束成形在某种最优准则下通过自适应算法来实现权集寻优,它能适应各种环境的变换,实时地将权集调整到最佳位置附近。
波束形成算法是在一定准则下综合各输入信息来计算最优权值的数学方法。如表1,这些准则主要包括最小均误差(MMSE)准则、最大信噪比(MSNR)准则和线性约束最小方差(LCMV)准则等[12]。
在电磁兼容现场测量中,由于需要提取EUT辐射信号的准确数据,所以,必须在抑制噪声干扰的情况下保持期望信号不失真。上述LCMV准则在满足线性约束条件wHα(θ)=1时,可以保证提取的EUT辐射信号不失真,这种方法也就是最小方法无畸变响应(MVDR)波束形成器。
为了有效抑制干扰,在获得空间信号DOA后,采用MVDR准则确定各阵元的最佳加权系数,对阵列方向图进行综合,使阵列主波束指向被测信号,并在干扰来向形成零点,尽可能保证被测信号不失真,最大化抑制干扰信号功率。MVDR在期望信号来向上增益为1。代价函数为J(w)=wHRw,约束条件为wHa(θ)=1。a(θ)为期望信号的方向相量。令
(11)
求式(11)的梯度并令其为零,得到
(12)
解得其权重向量为w=λR-1a(θ)
(13)
将式(13)带入约束条件中求得
(14)
将式(14)带入式(13)中可以求出最优权重向量为
(15)
4仿真实验结果
设接收阵列为8阵元的均匀线阵,间距为200 m。同时设空中有3个不同的信号,数学形式如下
(16)
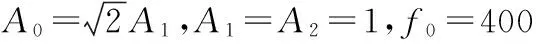
信号的来向分别为40°,20°,-20°,信噪比为10 dB。
4.1EUT和干扰信号来向仿真
通过经典MUSIC和CS算法对EUT辐射信号的DOA进行Matlab仿真得到实验结如图2。
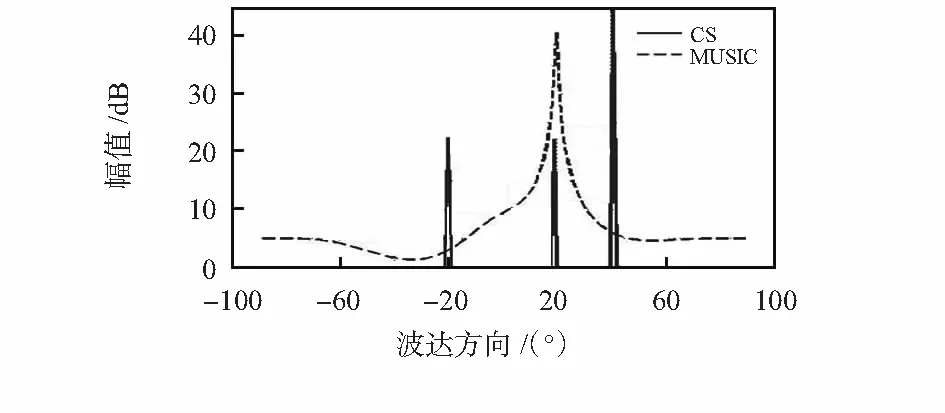
图2 MUSIC和CS的DOA估计结果Fig 2 DOA estimation results of MUSIC and CS
由图2可知:MUSIC在存在相干信号的情况下对EUT辐射信号和干扰信号的测向结果出现偏差,而CS-DOA算法可以准确获得EUT辐射信号和干扰信号的来向。同时CS-DOA估计算法对阵列结构没有限制,可以运用于非均匀限制情况,更加贴近实际应用。
4.2波束成形仿真
采用MVDR准则通过Matlab进行波束形成仿真得到结果如图3。
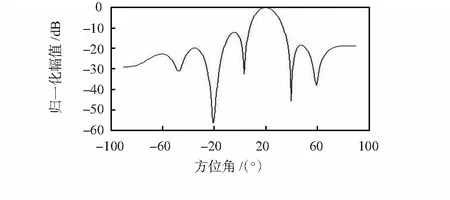
图3 MVDR波束形成结果Fig 3 Result of MVDR beamforming
如图3所示,阵列空间谱估计的主波束指向被测信号,不仅准确获取EUT辐射信号和干扰信号的DOA,而且在干扰来向处形成两个极深的“零陷”。
从图4、图5和图6是输入输出频谱对比,在保证期望信号失真的情况下,在300 Hz有效抑制噪声100 dB,在400 MHz的频谱峰值处与EUT原辐射信号抑制,该频率点的相干信号噪声基本被抑制,同时对其他频率的高斯噪声有0~25 dB的有效抑制。
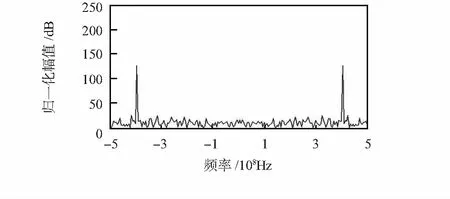
图4 EUT辐射信号的频谱Fig 4 Spectrum of EUT radiated signal
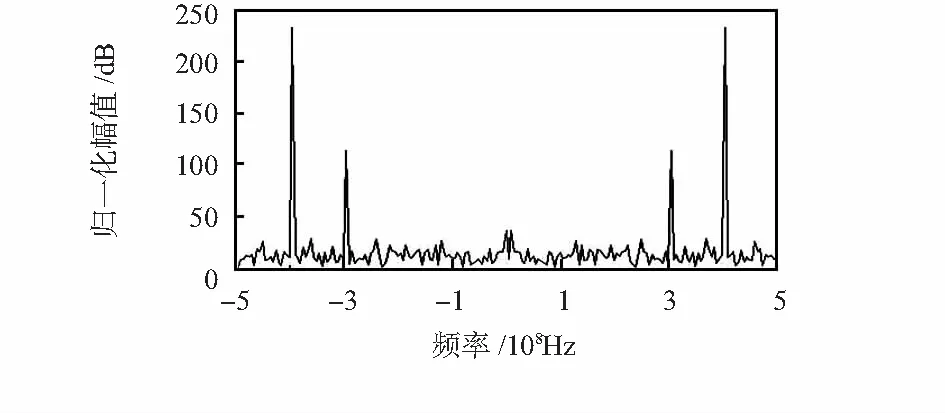
图5 阵列信号输入的频谱Fig 5 Spectrum of array signal input
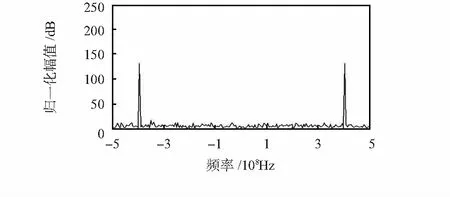
图6 阵列信号输出的频谱Fig 6 Spectrum of array signal output
5结论
本文提出一种基于CS的虚拟暗室技术用于解决现场电磁发射测量中相关信号干扰问题。该方法将CS理论、MVDR自适应波束形成技术引入到现场电磁兼容测试领域。通过仿真验证,该方法能够有效抑制现场辐射发射测试环境中的干扰信号,恢复出的EUT信号具有较好的保真度。该方法不仅可以应用在环境中存在相干信号的情况下,亦不受阵列结构限制,测试阵列可以根据测量场地的实际环境调整,在实际应用中更加灵活。
参考文献:
[1]Marino J,Michael A.System and method for measuring RF radiated emissions in the presence of strong ambient signals:US,6980611[P].2000—02—03.
[2]French A,Brauns S,Russer P.Time-domain EMI measurements
in the presence of ambient[C]∥Proc of the International Symposium on Electromagnetic Compatibility,2009:139-142.
[3]Dmochowski J P.Decoupled beamforming and noise cancella-tion[J].IEEE Trans on Instrumentation and Measurement,2007,56(1):80-88.
[4]Lu Z H,Liu P G,Liu J B.A novel method of ambient interference suppressing for in-situ electromagnetic radiated emission test[J].IEEE Trans on Electromagnetic Compatibility,2012,54(6):1205-1215.
[5]蒋伯峰,王文杰,殷勤业.适用于任意阵列的多径信道二维方向角与相对时延的联合估计方法[J].电子学报,2000(12):1-4.
[6]杨鹏,杨峰,聂在平,等.基于共形天线阵的免搜索来波方向估计算法研究[J].电波科学学报,2012,27(2):241-245,325.
[7]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[8]贺亚鹏,李洪涛,王克让,等.基于压缩感知的高分辨DOA估计[J].宇航学报,2011(6):1344-1349.
[9]Malioutov D,Cetin M,Willsky A S.A spare signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8):3010-3022.
[10] Cotter S F,Rao B D,Engan K,et al.Spare solutions to linear inverse problem with multiple measurement vectors [J].IEEE Transaction on Signal Processing ,2005,53(7):2477-2488.
[11] DaoB,Engan K,Cotter S F,et al.Subset selection in noise based on diversity measure minimization[J].IEEE Transaction on Signal Processing,2003,51(3):760-770.
[12] 张小江,汪飞,陈伟华.阵列信号处理的理论和应用[M].2版.北京:国防工业出版社,2013.
VirtualdarkchambertestmethodbasedonCS
ZHANGYao-wen,CHENShao-chang
(SchoolofElectronicEngineering,NavalUniversityofEngineering,Wuhan430000,China)
Abstract:In order to filtering out background noise effectively in on-site electromagnetic emission test,virtual dark chamber test method based on compressive sensing(CS)is proposed to solve the problem of failure of algorithm for multiple signal classification(MUSIC)when correlation signals exist in environment.Using theory based on CS to achieve directions of arrival(DOA) of radiation signal of equipment under test(EUT)and other interference signal in environment,and using minimum variance distortionless response(MVDR)bream-forming algorithm for beamforming,so as to effectively suppress interference signal.This method can not only be applied in the presence of coherent signals,but also has more flexible applications without restrictions in array structure. Simulation results prove that the method can suppress interference noise effectively without distortion of character of EUT.
Key words:virtual dark chamber; compressive sensing(CS); beamforming
DOI:10.13873/J.1000—9787(2016)04—0059—04
收稿日期:2015—07—08
中图分类号:TM 931
文献标识码:A
文章编号:1000—9787(2016)04—0059—04
作者简介:
章耀文(1992-),男,江苏苏州人,硕士研究生,主要研究方向为电磁兼容。
