打造高效课堂 凸显数学本质

沈党平

(江苏省新沂市第三中学，221400)

打造高效课堂凸显数学本质

沈党平

(江苏省新沂市第三中学，221400)

课堂是我们数学老师的主阵地,作为阵地中的引导者,要在短短的一节课45分钟的时间里,让学生的注意力全部集中到课堂中来,最大限度地去学习知识,提升思维品质,这一直是我们老师的追求．作为我们数学老师尤其是我们高三的数学老师应不断思考在课堂上如何去触及学生的情绪和意志领域,来打造高效课堂,凸显数学本质．本文笔者从两个方面对此作一些探讨,谈谈自己的看法．

一、一题多解，激活学生的思维

解法1建立如图1的坐标系,C(2,2)、D(0,2)圆弧EF的方程为

x2+y2=1(0≤x≤1).

设P坐标为(x,y)，则

=x2-2x+(2-y)2

=(x-1)2+(y-2)2-1.

解法2建立如图1的坐标系,C(2,2)、D(0,2)圆弧EF的方程为

x2+y2=1(0≤x≤1).

设P坐标为(x,y)，则

=x2-2x+(2-y)2

=x2+y2-2x-4y+4.

解法3建立如图1所示的直角坐标系,C(2,2)、D(0,2)圆弧EF的方程为

x2+y2=1(0≤x≤1).

设P坐标为(cosθ,sinθ)，则

(-cosθ,2-sinθ)

=5-2cosθ-4sinθ

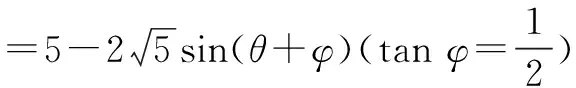
二、多题一解，提升学生思维品质

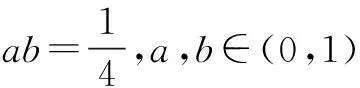
本题是填空题的压轴题,属于难题,从学生的得分情况来看,学生做的很不理想．本题主要考查了利用基本不等式来处理二元最值问题，考查了这部分内容中最常用的一种处理方法常值代换、转化与化归等数学思想方法．这类题型实质上是课本中的一个习题的变式．

原型题作为基本不等式这节中最为典型的一个习题,其处理方法比较多,其中较为简单的处理方法是“常值1”的代换．具体的解题过程如下:

由x+2y=1,得

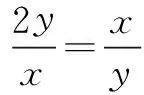
具体的解题过程如下:

由x+2y=3,得

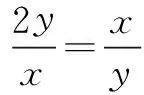
变式2(模式改变)已知正数x、y满足x+y=xy,求x+2y的最小值为______．

变式2可借助基本不等式利用常值代换来解决这类题,这类题型的基本模式是两个和式且其中一个是分式的形式．所以，这题要将已知条件的整式两边同时除以xy,即可变成我们的基本模型了．具体的解题过程如下:

因为正数x、y满足x+y=xy，所以有

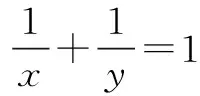
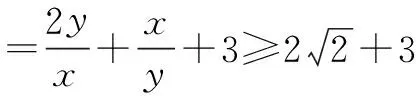
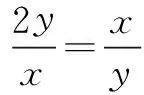
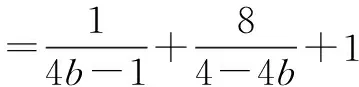
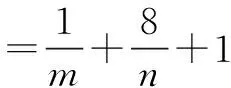
变式4是在变式3的基础上再次进行拓展延伸.将已知条件中的等号改为不等号,同时还有对结构进行构造,所以本题对学生的基本知识、基本能力要求较高．

具体的解题过程如下:

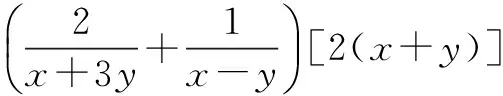
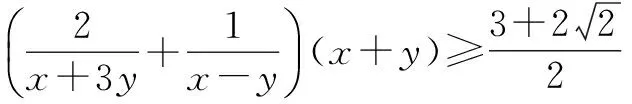
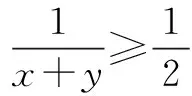
将上面两个式子相乘，得

三、教学反思

数学教学尤其是作为高三的数学教学,从某种程度上说就是一种解题的教学.但在教学过程中,不能就题讲题,满足于完成这一题得出结果,否则就不能够让我们学生从茫茫的题海中解脱出来,因此，“一题多解”、“多题一解”就显得尤为重要了．“一题多解”能够激发学生学习的兴趣,培养学生发散思维,开拓学生思路,是激发学生思维品质的一种教学手段．教师要诱导学生多角度、多层次思考问题,激活学生思维的发散性和创造性.“多题一解”可以让学生有梯度地深入难点,引导学生将一些经过迁移的交汇知识进行归纳总结.这样可以提高教学的有效性,提升学生的思维品质．

另外，在高三复习中,教师要立足课本,回归课本．从最近几年的高考试题和高三的模拟考试试题中可以发现,有很多题目都来源于课本,都能在课本上找到原型．故我们要强化对课本典型例题、习题的研究,不能简单地就题论题,要注重引导学生进行一题多解、一题多变、一题多解,追根溯源,引导学生从不同的角度去观察问题,思考问题,从而使学生的思维从单一走向多维,提高课堂的高效,优化学生的思维．

更多或更优的解法,此类问题是否能进一步推广,等等．