浅议发散性思维与聚合性思维的培养

黄怡皖

(江苏省吴江中学，215200)

浅议发散性思维与聚合性思维的培养

黄怡皖

(江苏省吴江中学，215200)

数学是一场思维的盛宴.正所谓“授之以鱼不如授之以渔”，要想从根本上提升学生的数学水平，必须让学生学会各种数学思维方法，学会灵活运用.培养学生发散性思维和聚合性思维，开启学生的创造之门是教师的职责，是实施素质教育，提升学生科学素质、实现民族振兴的重要任务.

一、发散性思维与聚合性思维的特性

如果将人的思想比作一条源远流长的大河，那么这条大河源头是“实践”，“认识”自源头流出形成河流的雏形.后来这条河流分成了两个支流，那便是“发散性思维”与“聚合性思维”.这两大支流又各自衍生出层级众多、纵横交错、无孔不入的许多支流，这些支流就是各种思维方法.

那么，发散性思维与聚合性思维到底是什么呢？首先从字义的角度解释，发散性思维又称之为求异、扩散思维，它是一种从不同的方面去假设，猜想多种答案，最终使问题全面解决的思维方法.聚合性思维又称为求同思维、集中思维，意味着思维者把与要解决的问题相关的内容聚集在一起，从而在解决问题时，进行重组获得唯一答案的收敛式思维方式.同样，在教学运用中以实例说明：就是拿到任何一道数学题，首先要读题，然后要搜集原题中的所有用信息然后进行筛选、翻译、重组，构建成人们头脑中的知识与方法网络.之后调动头脑中所有可能有用的或用得到的知识与方法，再次进行筛选、翻译、重组，最终构建出解题思路.这一过程中，“搜集”与“调动”、“筛选”是聚合性思维，也称“归纳”；“翻译”与“重组”、“构建”是发散性思维，也称“演绎”或“模拟”.拉普拉斯说：“在数学中，我们发现真理的主要工具是归纳和模拟.”正是一语道破玄机.

发散性思维与聚合性思维并非彼此独立的，他们的产生没有先后之分，性质没有高下之别，他们是同时产生、相辅相成的.聚合思维是基础，发散思维是在其基础上的拓展与延伸；聚合性思维是对于发散性思维的凝聚，使发散思维更具有同一性.只有合理地运用两种思维才可以圆满地解决问题.

二、发散性思维与聚合性思维的培养

精通数学的人都知道，越是复杂、高深的难题，往往它方法越是简单、浅显,真正难的是思考与探索的过程.如果将发散性思维与聚合性思维的养成看做一道难题，它的解决方案也是平凡简单乃至琐碎的，但方案背后的良苦用心却值得我们深思.

首先，要将这两种思维的培养渗透到所有教学活动中.不仅在知识发生过程中，而且也在问题的解决过程中培养这两种思维；不仅在知新中感悟，而且也在温故时运用这两种思维.而且不仅在课堂教学中传授，而且也在课外生活中锻炼这两种思维，尤其是在高中数学的教学过程中应更加注重两种思维的结合.

下面，以一道高中数学组合题为例，来了解发散思维与聚合性思维是怎样融合运用的.

题目从6台液晶电视机与5台数字电视机中任意选取5台，其中至少有液晶与数字电视机各2台，则不同的取法有多少种.

错解因为可以取2台液晶电视机与3台数字电视机或是3台液晶电视机与2台数字电视机，由此可知只有两种方法.

错因分析错解是因为在于没有意识到“选取2台液晶电视机与3台数字电视机或是3台液晶电视机与2台数字电视机”是完成任务的两类办法，每类办法中都还有不同的取法.

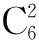
在这道题的解答中，教师自始至终没有讲解，教师只是给出了最初的方向，然后学生们顺着这个方向想下去.当思路转折时，教师给出指引，当思路断裂时，教师给出点拨.学生通过多种角度解决问题发现其他不同的解法，化复杂为简单，变抽象为直观，运用多角度的思考方式，从而最大限度地提高了学生思维的发散水平，达到算法多样化.这道题的解答运用了排列组合，整体思想等多种知识，需要多次转化，这种知识与步骤的整合过程便是聚合思维的过程.

由以上例子可见，要想成功渗透思维方式，就必须改变老师讲学生听的传统授课方式，巧妙地启发学生自主思考.课堂之外的渗透方式有很多，比如组织学生讲一些关于数学的故事，玩一些关于数学的益智游戏等.除了润物无声的渗透，还要进行一些专门的强化训练.主要是两方面：一方面是针对发散性思维，可以训练一题多解，让学生自己编题目自己做，有意识地进行数学问题的联想，等等.另一方面是针对聚合性思维，可以有意识地让学生们做一些题干长条件多的题，专门训练提取有用信息的能力.此外，注意在每节新课结束后让学生归纳所学内容，让学生们定期总结题型，在类型题讲解结束后让学生提炼解题规律，等等.

三、关于培养发散与聚合思维的进一步思考

第一，我们不要忘了“功夫在诗外”的道理.我们必须让学生们理解思维的奥妙，深刻认识发散性思维与聚合性思维的重要性.让学生养成爱思考的习惯，将这种理性思维精神内化成自己的行为方式，生活方式，生命特质，而不仅仅是一种数学做题方法.

第二，教师在高中数学的教学中，应该从班级学生的认知水平出发，从数学的概念、语言以及解决问题的方法等等全方位探讨，进而拓展解题的思路.在讲解题目的过程中应该选择学生众所周知的途径，通过观察、尝试、以及手脑并用等多种方法去亲临感受，从而给予学生启发与联想，使思考更加深刻.

第三，兴趣是学生最好的老师.培养学生的学习兴趣是促进学生的发散思维与聚合性思维的行之有效的手段.对此，我们应从两方面做起，一方面用原有的知识做基础进行一下场景的变换与设计，从而激发学生寻求新知识的兴趣；另一方面设置悬念，引导学生产生疑问，从而引导学生进行积极的思考与探索.

第四，静水深流.数学不同于语言类学科，不崇尚口舌之巧.恰恰相反，我们应该让学生学会静，静下心来，才能深入思考，细细体悟，让思维之河恒定流淌.