浅析学生数学思维能力的培养
2016-06-24何新艺
何新艺
(江苏省东台市三仓中学,224231)
浅析学生数学思维能力的培养
何新艺
(江苏省东台市三仓中学,224231)
随着教育体制改革的不断深化以及新课程标准的提出,教学中,除了知识的传递,思维的激发和能力的培养越来越受到广大教育者的重视.学生是祖国的未来,是社会的希望,如何在教学中充分地激发和引导学生的创造思维,使学生获得综合能力的提高,是每个教师潜心探讨的话题.
一、借助直观教学启迪学生思维的积极性
教师必须在教学中积极地调动学生学习数学的主动性,充分地体现学生在学习中的主体地位,激活学生进行数学知识学习的思维.教师在实施课堂教学的过程中要善于与学生进行知识教育及思维的交流,并且借助于典型的直观问题来组织学生开展自主的探讨、研究,引导学生真正放心大胆地开拓自己的思维来学习数学知识.
案例1在探索椭圆的概念教学时,为了有效引导同学们探究解决问题,笔者采用实践的方法启迪学生的思维.首先要求同学们取出事先准备好的学具,把细线的两端固定在两个小图钉上,用水笔将长度为l细线拉紧,让笔尖在纸上慢慢移动,画出了一个图形.之后,笔者引导学生思考回答下列问题:
问题1画出了一个什么图形?
问题2这个图形上的点有何特征?
问题3如果l等于两定点之间的距离时,它的轨迹是怎样?
问题4如果l小于两定点之间的距离时,它的轨迹又怎样?
问题5你们能给椭圆下一个定义吗?
由于同学们亲手实践,讨论问题的积极性很高,师生互动,效果佳;最后师生一起揭示本质,给出定义.笔者运用这种方法,让同学们通过感性认识之后,进行分析思考,对椭圆定义有了深刻的理解,从而在今后遇到这类问题,就不会出现错误.
二、运用变式问题,培养思维的灵活性
思维的灵活性是指思维活动的灵活程度,即运用新观点观察变化的事物,并提出新的解决方法.数学教育不是看学生掌握了多少知识点,看学生会解答多少道数学题,而是看学生的数学能力是否得到发展.由于传统教法的影响,学生大多数习惯题海战术,而缺少思考的时间、空间,在学习中不能举一反三,应变能力较低.因此,教师要把培养学生思维的灵活性放在重要的位置,以新颖的例题或设计多变的题型来训练他们思维的灵活性.
案例2在进行函数极值教学时,为了有效地训练学生思维,引导同学们自主探索,笔者进行了如下问题的变式设计:
问题已知函数
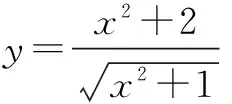
试求函数的最小值.
同学们根据所学知识,在小组中很快就探究出解题方法,并得结果,他们的情绪高涨.紧接着,笔者抓住时机进行下列变式.
变式1已知函数
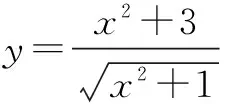
试求函数的最小值.
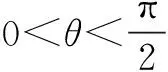
变式3已知函数
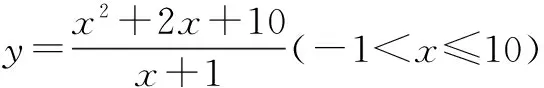
试求其最小值.
要求同学们以小组为单位,看哪一小组完成最多,最佳.这下,同学们在小组里思维活跃起来,研究气氛十分浓厚.这样,函数问题一题多变,学生在求极值时,能有效地运用所学知识,着手解决函数极值问题,体验到运用数学知识来解决实际问题的乐趣.
三、分析解题出错原因,培养思维的深刻性
通过平时的教学发现,大多学生对知识的理解不够深入,甚至有些学生知识的掌握只是浮光掠影式的.做习题时,只会套用例题,依葫芦画瓢;对一些定理、公式等,根本不去思考是否适合所有的情况,有没有特例等.以上种种都需要教师的适时适当地引导和启发.
案例3在进行了指数运算教学时,笔者设计了如下一组化简题:
学生板演结果错误百出,如
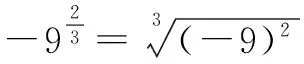
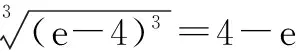
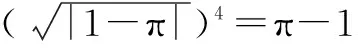
从学生的错误解答可以分析出学生并没有真正理解指数的意义及运算顺序,知识单一,新旧知识混淆,思维混乱.学生自己不能找出错误原因,这时老师需要适时指导,帮助学生梳理新旧知识之间的联系,切不可批评指责.因此,在新授课中,教师要特别注意知识的引入方法与技巧,学生对知识的第一印象特别重要,切不可炒“夹生饭”,留“后遗症”.
四、鼓励一题多解 培养思维的创造性
创造性作为民族生存之本,是人类最有活力的行为,是科学研究的第一要义和生命线.培养学生创造性思维能力是素质教育的基本要求,它有利于培养学生的创新意识和创新精神.
鼓励学生一题多解,能够引导学生解题时不落俗套、不拘一格,努力尝试用多种方法,从各个不同角度和不同途径去寻求问题的答案,有利于培养学生的创造性思维.
案例4已知a,b∈R,a2+b2=1,求2a+b的范围.
解法1(转化为一元二次方程有实根的问题)
令2a+b=t,得b=t-2a.
由a2+b2=1,得
5a2-4ta+t2-1=0,
∵Δ=(-4t)2-4×5(t2-1)≥0,
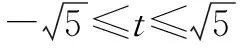
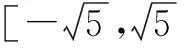
解法2(利用数形结合转化为直线与圆有公共点问题)
令2a+b=t,得2a+b-t=0,
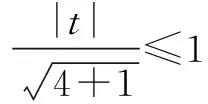
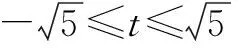
解法3(利用圆的参数方程,转化为三角函数求解)
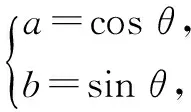
2a+b=2cosθ+sinθ
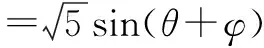
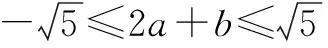
数学思维方式不是一朝一夕便能形成的,教师和学生应积极配合,根据主观条件,适当地调入客观资源,根据学生的实际情况和教师的教学策略灵活变通地进行思维培养和训练,才能够促学生数学思维能力的不断提高.
