一种自适应Morlet小波滤波方法及其在滚动轴承早期故障特征提取中的应用
2016-06-24贾民平
张 菀 贾民平 朱 林
(东南大学机械工程学院, 南京 211189)
一种自适应Morlet小波滤波方法及其在滚动轴承早期故障特征提取中的应用
张菀 贾民平 朱林
(东南大学机械工程学院, 南京 211189)
摘要:针对滚动轴承早期故障信号微弱,故障特征难以提取的问题,提出了一种基于混洗蛙跳算法(shuffled frog leaping algorithm,SFLA)的自适应Morlet小波滤波方法.首先利用自相关分析去除宽频随机噪声,然后通过SFLA优化Morlet小波的滤波参数,获得在最小信息熵下的中心频率和滤波带宽.由自适应Morlet小波滤波器获得的滤波信号,其中的冲击成分可以很好地被表征.最后对滤波后的信号做包络谱分析即可提取滚动轴承的故障频率.实验表明,自适应Morlet小波滤波方法可以成功地从低信噪比信号中提取出周期冲击特征,对于滚动轴承早期故障振动信号,能够有效地提取冲击特征频率实现滚动轴承早期故障诊断.
关键词:滚动轴承;特征提取;早期故障;Morlet小波;混洗蛙跳算法中图分类号: TH165.3;TH17
文献标志码:A
文章编号:1001-0505(2016)03-0457-07
滚动轴承是机械设备中应用最广泛的零件之一,也是旋转机械易损件之一[1].滚动轴承在使用过程中经历正常、早期微弱故障、严重故障到失效的过程.严重故障阶段意味着滚动轴承已经发展到故障中晚期,故障特征明显且容易提取;早期微弱故障阶段的特征提取相对来说比较困难,因为早期阶段故障特征微弱,且其他运动部件的信息以及环境干扰也会被引入到轴承系统中而形成背景噪声,从而使得轴承的早期故障难以监测和诊断.若能对早期故障特征进行提取和故障诊断,采取主动的维修策略,则可有效地避免灾难性事故和人员伤亡.
针对滚动轴承发生故障时所具有的非平稳特征,国内外学者对滚动轴承早期故障特征提取方法进行了大量的研究.目前在滚动轴承故障诊断中广泛应用的方法主要有小波变换、经验模态分解(empirical mode decomposition,EMD)和谱峭度等非平稳信号分析方法.从小波滤波降噪方面考虑,Bozchalooi等[2]利用平滑指标选择Gabor小波的尺度和形状参数,而这2个参数分别对应于带通滤波器的中心频率和带宽.Qiu等[3]结合了香农熵和奇异值分解理论来获取最优小波变换系数,从而达到降噪的目的.Wang等[4]基于模拟退火算法自适应获取Morlet小波的滤波参数,并采用最大稀疏函数作为适应度函数,但此方法并不适用于早期故障诊断.Zhang等[5]利用峭度图获得初始带通滤波参数,再基于遗传算法进一步优化带通滤波器中的6个参数,其中适应度函数采用峭度,而峭度对噪声敏感,故该算法的鲁棒性较差.胡爱军等[6]采用形态滤波的方法提取旋转机械的故障特征,但该方法在消除脉冲型噪声的同时也容易削弱微弱故障特征.
SFLA是Eusuff等[7]于2003年提出的一种基于群体的亚启发式协同搜索群智能算法.SFLA结合了模因演算法和粒子群算法,具有概念简单、参数少、计算速度快、全局寻优能力强、易于实现等特点[8].基于SFLA自适应地获取Morlet小波的滤波参数,采用信息熵作为SFLA的适应度函数,其优点在于信息熵是信号不确定性的一种度量,可以很好地表征混合信号中的周期冲击成分.本文首先对滚动轴承故障信号进行自相关分析,滤除宽频随机噪声.再基于SFLA获取最小信息熵下的带通滤波器参数,对滤波后信号进行包络解调分析,即可获得滚动轴承的故障特征频率.最后结合NSF I/UCR中心滚动轴承的全寿命实验数据对该算法进行验证.
1自适应Morlet小波滤波算法
当滚动轴承出现局部损伤后,其各部件之间的相对周期性运动引起损伤部位产生周期性冲击,故滚动轴承的故障信号模型具有周期性的冲击特征.在滚动轴承早期故障阶段,由故障所引起的冲击成分不仅幅值小,而且由于背景噪声的影响使得轴承早期故障特征不明显.早期故障特征幅值小,淹没在噪声信号中.为了增强早期故障特征,本文通过合理地设计带通滤波器获得高频瞬态成分,滤除低频机械转频和宽频随机噪声,对高频瞬态成分做包络解调分析,即可获得故障特征信息.
1.1自相关分析
由于滚动轴承故障信号包含周期性冲击信号、机械转频信号和噪声信号,而早期故障特征通常被背景噪声淹没,如何去除随机噪声是前处理阶段的主要任务.通常随机噪声具有宽频带特征,若对宽频随机噪声进行自相关分析,发现其迅速衰减到零,故本文在前处理阶段采用自相关分析.定义自相关函数rxx(τ)为
rxx(τ)=E[x(t)x(t+τ)]τ=0,1,2,…,N-1
(1)
式中,τ为时移滞后指标;E[·]为数学期望算子;N为采样点数.自相关分析是区别信号类型的一种有效手段,只要信号中含有周期成分,其自相关函数在τ很大时都不衰减,并具有明显的周期性.而对于不包含周期成分的随机信号,当τ稍大时自相关函数将趋近于零.机器在运转过程中的振动噪声一般是大量的、无规则的随机扰动的结果,利用自相关分析可以很好地去除随机噪声.
1.2Morlet小波
为了更好地提取滚动轴承早期的故障特征,选择用Morlet小波构造合适的带通滤波器,从而实现对高频瞬态成分的提取.Morlet小波定义为
(2)
式中,fb为带宽;fc为中心频率.对实信号分析采用式(2)的实部作为基小波,则有
(3)
Morlet小波的傅里叶变换为
ψ(f)=exp[-π2(f-fc)2/fb]
(4)
由于Morlet小波函数为平方指数衰减的余弦信号,其波形与冲击信号十分相像,采用Morlet小波为小波基函数较为合适.图1(a)为Morlet小波的时域波形,fc的变化直接影响Morlet小波的振荡频率,fb的变化影响Morlet小波振荡的衰减时间.图1(b)为Morlet小波的频谱图,从图中可知,改变fc和fb即可以改变滤波特性.通过卷积特性和傅里叶变换,在频域范围内Morlet小波对被分析信号的滤波过程可以写成
(5)
式中,x(f)表示x(t)的傅里叶变换.通过构造合适的ψ(f)即可实现带通滤波,获得故障信号中的高频瞬态成分.

(a) 时域
1.3混洗蛙跳算法
采用Morlet小波构造带通滤波时,滤波参数fb和fc的选择对故障特征的提取效果起着关键作用.本节主要利用混洗蛙跳算法(SFLA)优化带通滤波参数fb和fc.由于信息熵是信号的不确定度,信号越不确定,信息熵越大.当信号中冲击成分越多时,信号越确定,信息熵越小,故采用信息熵作为SFLA的优化指标.SFLA的计算过程如下:

(6)
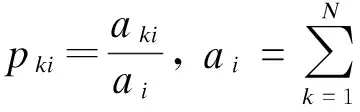
当所有族群完成指定迭代次数的深度搜索后,所有青蛙将重新混合并排序,更新群体最佳青蛙位置,然后重新划分族群,重新进行局部深度搜索,如此循环直到满足终止条件.
1.4自适应Morlet小波的故障特征提取
基于SFLA的自适应Morlet小波滤波方法的核心是:通过随机生成二维参数(fic,fib),根据SFLA来获得优化后的滤波参数(foptc,foptb),而滤波参数获取的依据是在该组参数下带通滤波后的信号信息熵最小.采用信息熵作为适应度函数的优点是信息熵可以很好地表征周期冲击信号,在自适应带通滤波参数下滤波后的信号必然表现出很好的冲击特性,对滤波信号再做包络谱分析即可获得早期的故障特征频率.算法流程如图2所示.

图2 自适应Morlet小波算法流程图
2仿真
2.1适应度函数的选择
适应度函数的选择既要满足表征故障特征的要求,还需要考虑对噪声不敏感.为了说明信息熵表征冲击成分的有效性,讨论峭度和信息熵对滤波参数的影响.
建立如下仿真信号模型:
s(t)=s1(t)+s2(t)+s3(t)
(7)
式中,s1(t)=e-400tcos(2π×4 365t),s2(t)=0.5sin(2π×1 000t),s3(t)为白噪声信号.仿真信号的频谱如图3所示.

图3 仿真信号的频谱图
为了说明SFLA在选择熵值作为适应度函数时可获得适合的滤波参数,对不同滤波参数下的峭度和熵值进行讨论.当中心频率固定为4.3 kHz,滤波带宽变化范围为(200,3 000)Hz时,获得的峭度和熵值随带宽的变化曲线如图4(a)和(b)所示.由图4(b)可知,当fb=1.5 kHz时熵值最小,而图4(a)中峭度随滤波带宽的增大而增大,过大的滤波带宽会引入更多的噪声,在最大峭度值处无法获得准确的滤波带宽.图4(c)和(d)是滤波带宽为1.5 kHz、中心频率在(100,5 000)Hz范围内的峭度值和熵值的变化曲线.由图4(d)可知,当中心滤波频率为4.3 kHz时熵值达到最小,和设置的s1(t)中心频率4.365 kHz相近;由图4(c)可知,当中心频率为3.0 kHz时峭度达到最大值,显然与s1(t)的中心频率4.365 kHz不一致.由于早期故障阶段的冲击特征通常淹没在噪声信号中,峭度容易受噪声影响,选择熵值作为适应度函数时可以获得较为准确的滤波参数.

(a) 峭度,fc=4.3 kHz
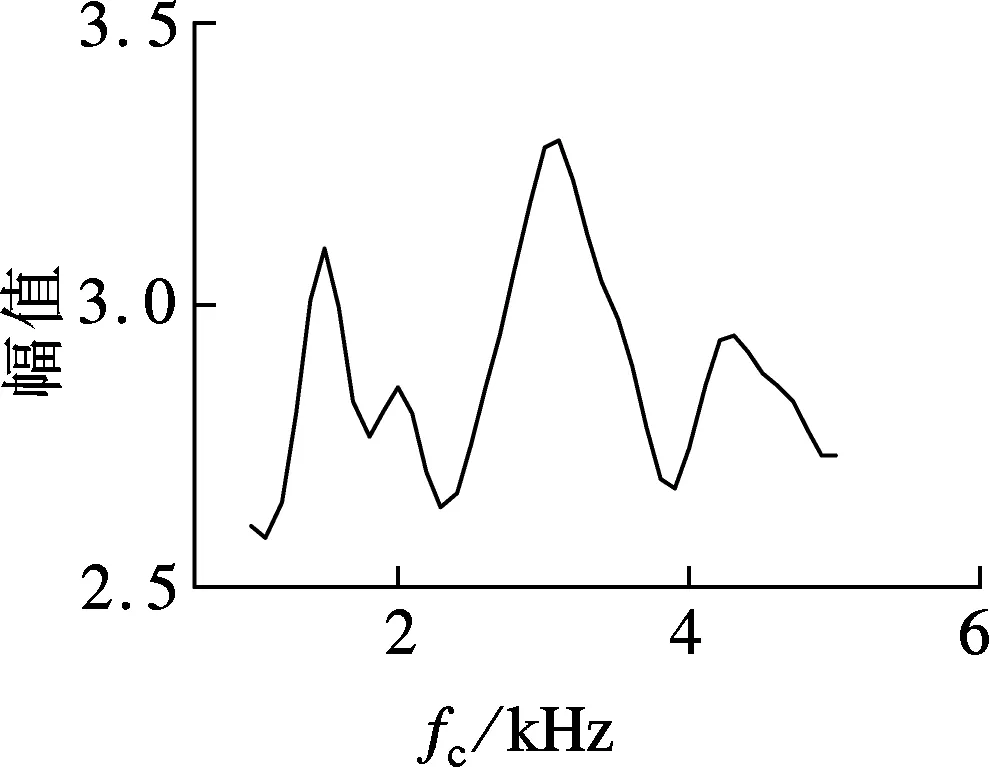
(c) 峭度,fb=1.5 kHz
2.2仿真信号分析
为了验证自适应Morlet小波算法的有效性,将实际滚动轴承故障信号模型进行简化,建立如下滚动轴承故障信号的仿真模型:
s(t)=s1(t)+s2(t)+s3(t)
(8)
t=mod((0:1 023)/1 024,1/10)
(9)
式中,信号s1(t),s2(t)和s3(t)分别表示故障轴承信号中的故障成分、机械转频信号和背景噪声.s1(t)=e-80tsin600πt,s2(t)=sin40πt,s3(t)为均值为0、方差为1的白噪声信号.图5(a)~(d)分别为s1(t),s2(t),s3(t)和s(t)仿真信号.
2.2.1参数设置
优化算法中的参数设置会直接影响到算法的收敛性,因此在进行自适应Morlet小波降噪前,需要合理地设置SFLA的参数.设青蛙数为100,共分为m=10个种群,每个种群中有n=10只青蛙个体,子种群中有q=7只青蛙.设置青蛙解空间为二维,fc搜索区间为(0,500)Hz,fb搜索区间为(0,400)Hz,蛙跳步长限定范围为(-100,100)Hz,算法组内迭代次数Ne=5,算法全局迭代次数Nc=30.

(a) s1(t)

(b) s2(t)

(c) s3(t)

(d) s(t)
2.2.2仿真结果分析


(a) 滤波后的幅值谱
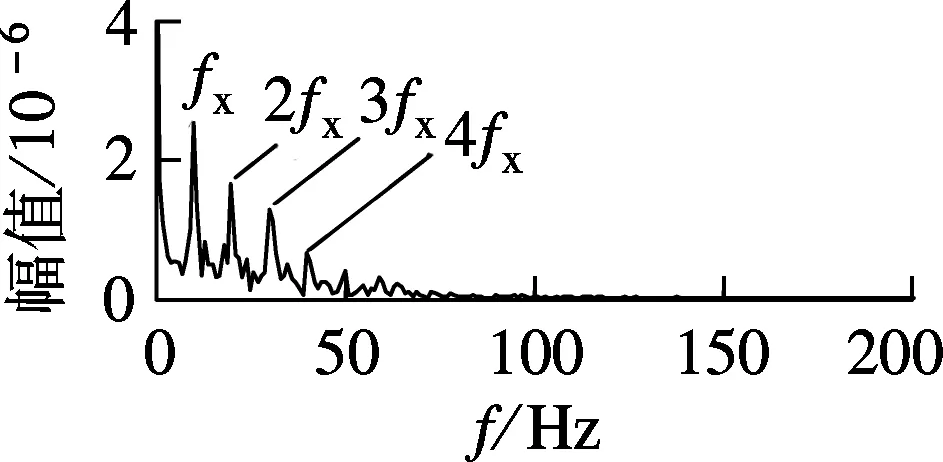
(c) 滤波后信号包络谱
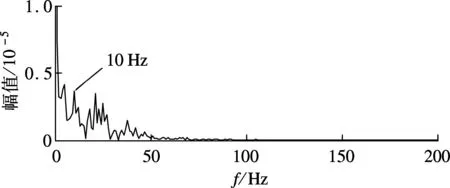
图7 滤波参数为{186,65}Hz时滤波信号的包络谱
集合经验模态分解(ensemble empirical mode decomposition,EEMD)是常用的非平稳信号处理方法,图8为采用EEMD分解的IMF1分量的包络谱,这里忽略其他IMF分量,因为IMF1分量方差贡献率为54.63%,从图8中得到fx和其倍频,但其峰值并不突出.为了进一步说明该算法的有效性,采用文献[9]中Fast Kurtogram算法对仿真信号进行分析,结果如图9(a)所示,得到最大谱峭度值处中心频率为304 Hz,滤波带宽为32 Hz.使用该滤波器对仿真信号进行滤波,滤波后信号包络解调得到的包络谱如图9(b)所示,图中出现冲击特征频率fx的前2个倍频,而在图6(c)中出现冲击特征频率fx的前4个倍频.本文的方法较Fast Kurtogram能更大程度上保留共振带的信息,更有利于微弱冲击特征的提取.

图8 EEMD分解的IMF1分量的包络谱

(a) 谱峭度图

(b) 谱峭度最大值对应的解调谱
3实验
为了在实验中检验算法的有效性,将自适应Morlet小波滤波算法应用于实际滚动轴承实验.采用美国智能维护中心NSF I/UCR的轴承疲劳寿命试验数据,实验装置简图如图10所示[3].

图10 疲劳寿命实验台简图
滚动轴承型号为ZA-2115,实验工况为:输出转速2 000 r/min,径向载荷26.6 kN,采样点数为20 480,采样频率为20 kHz.实验中每次采样持续1 s,每10 min记录一次,一共记录了984组振动信号,最终轴承1外圈出现严重故障而失效.
图11为滚动轴承全寿命过程中幅值均方根的变化曲线.根据文献[10]中提到的在疲劳寿命前期(前540个点)轴承处于健康状态,而故障状态是从第541点开始,将第541点定义为滚动轴承早期故障点进行分析.图12(a)和(b)分别给出第541点轴承早期故障时域图及频谱图.从时域图和频谱图中无法判断故障类型,因而需要对信号做进一步处理.

图11 滚动轴承1全寿命周期的幅值均方根值

(a) 时域信号

(b) 频谱图

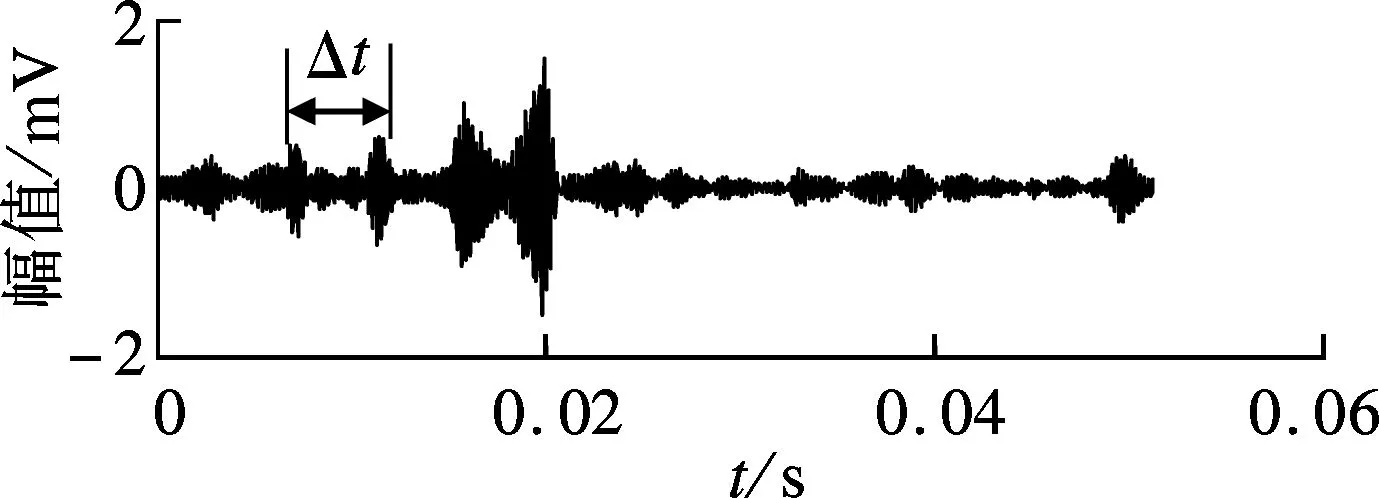
(a) 滤波后时域图

(b) 图(a)的包络谱

(c) 适应度函数的迭代曲线

参数数值参数参数值种群规模10×10fc搜索区间/kHz(0,6)子种群规模7fb搜索区间/kHz(0,3)子种群内更新代数5fc步长区间/kHz(-1,1)全局迭代次数30fb步长区间/kHz(-1,1)
图14为采用EEMD对轴承外圈故障信号进行分解后得到的IMF1分量的包络解调谱.图中峰值即为外圈故障特征频率,从图中只能得到不明显的故障特征频率fo.采用Fast Kurtogram算法对实验信号进行分析,得到的谱峭度图如图15(a)所示.谱峭度最大值对应的中心频率为8.333 kHz,带宽为3.333 kHz,此时最大峭度值为1.1,该频带的解调谱如图15(b)所示,从图中可以得到故障特征频率fo,但宽频的随机噪声的幅值也接近于故障特征频率的峰值.通过实验分析,本文方法首先采用自相关分析滤除宽频随机噪声,然后通过自适应Morlet小波获得滤波参数,增强故障特征.与其他2种算法相比,本文方法可以得到故障特征频率及其多个倍频信息,更有利于故障诊断.

图14 EEMD分解的IMF1分量包络解调谱
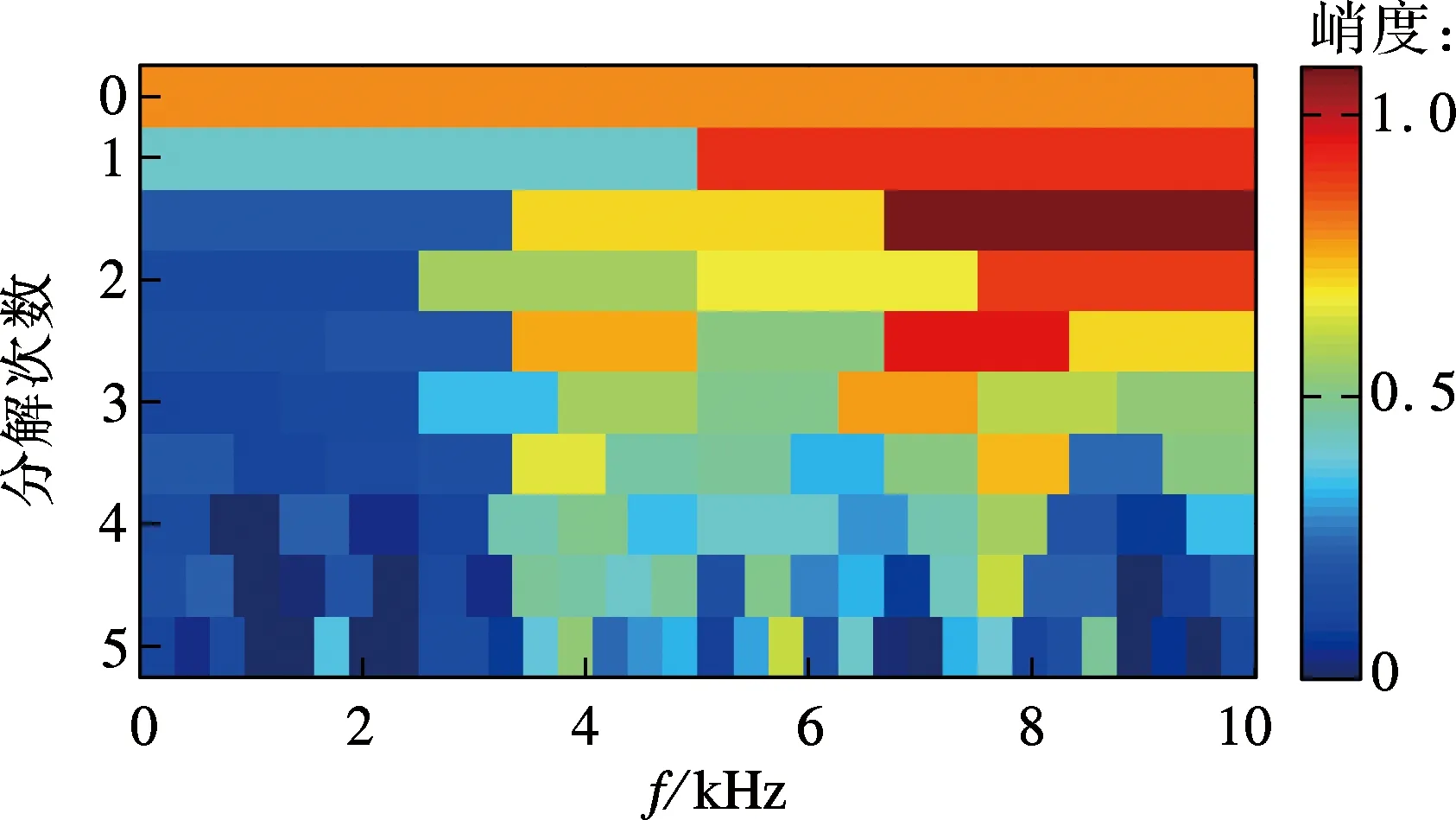
(a) 谱峭度图

(b) 谱峭度最大值对应的解调谱
4结论
1) 本文基于SFLA提出一种自适应Morlet小波滤波算法.首先利用自相关分析滤除宽频随机噪声,然后基于SFLA优化Morlet小波的滤波参数,对自相关分析后的信号进行进一步带通滤波,滤波后信号的周期冲击特征可以被很好地表征.
2) 为了选择合适的适应度函数来表征故障特征,从而得到故障信号中的高频瞬态成分.比较了峭度和信息熵对滤波参数的影响,将信息熵作为适应度函数时,可以准确地获取带通滤波参数.
3) 将自适应Morlet小波滤波算法应用于滚动轴承早期故障信号,能有效地提取出淹没在噪声中的冲击成分,从而根据冲击成分的包络谱进行滚动轴承早期故障诊断.
参考文献 (References)
[1]钟秉林,黄仁,贾民平.机械故障诊断学[M].北京:机械工业出版社,2013.
[2]Bozchalooi I S, Liang M. A joint resonance frequency estimation and in-band noise reduction method for enhancing the detectability of bearing fault signals[J].MechanicalSystemsandSignalProcessing, 2008, 22(4): 915-933.
[3]Qiu H, Lee J, Lin J, et al. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics[J].JournalofSoundandVibration, 2006, 289(4/5): 1066-1090. DOI:10.1016/j.jsv.2005.03.007.
[4]Wang D, Guo W, Wang X J. A joint sparse wavelet coefficient extraction and adaptive noise reduction method in recovery of weak bearing fault features from a multi-component signal mixture[J].AppliedSoftComputing, 2013, 13(10): 4097-4104. DOI:10.1016/j.asoc.2013.05.015.
[5]Zhang Y X, Randall R B. Rolling element bearing fault diagnosis based on the combination of genetic algorithms and fast kurtogram[J].MechanicalSystemsandSignalProcessing, 2009, 23(5): 1509-1517. DOI:10.1016/j.ymssp.2009.02.003.
[6]胡爱军,唐贵基,安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报,2006,42(4):127-130.
Hu Aijun, Tang Guiji, An Liansuo. De-noising technique for virbation signals of rotating machinery based on mathematical morphogy filter[J].JournalofMechanicalEngineering, 2006, 42 (4): 127-130. (in Chinese)
[7]Eusuff M, Lansey K. Optimization of water distribution network design using the shuffled frog leaping algorithm[J].AmericanSocietyofCivilEngineers, 2003, 129(3): 210-225.
[8]Eusuff M, Lansey K, Pasha F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization[J].EngineeringOptimization, 2006, 38(2): 129-154. DOI:10.1080/03052150500384759.
[9]Antoni J. Fast computation of the kurtogram for the detection of transient faults[J].MechanicalSystemsandSignalProcessing, 2007, 21(1): 108-124. DOI:10.1016/j.ymssp.2005.12.002.
[10]胡世杰,钱宇宁,严如强.基于概率密度空间划分的符号化时间序列分析及其在异常诊断中的应用[J].振动工程学报,2014,27(5):780-784. DOI:10.3969/j.issn.1004-4523.2014.05.019.
Hu Shijie, Qian Yuning, Yan Ruqiang. Anomaly detection using symbolic time series analysis based on probability density[J].JournalofVibrationEngineering, 2014, 27(5): 780-784. DOI:10.3969/j.issn.1004-4523.2014.05.019. (in Chinese)
An adaptive Morlet wavelet filter method and its application in detecting early fault feature of ball bearings
Zhang Wan Jia Minping Zhu Lin
(School of Mechanical Engineering, Southeast University, Nanjing 211189, China)
Abstract:Considering the early fault of ball bearings being weak and the difficulty of detecting the fault feature, an adaptive Morlet wavelet filter method based on shuffled frog leaping algorithm (SFLA) is proposed. First, the auto-correlation analysis is utilized to filter the broadband random noise. Then, the optimal center frequency and the filter bandwidth under the minimum information entropy are acquired by optimizing the filtering parameters of Morlet wavelet through SFLA. The filtered signal can be obtained by applying the adaptive Morlet wavelet filter, and the impulse features can be well highlighted. Finally, the filtered signal is analyzed by the envelope spectrum to extract the fault frequencies of the ball bearings. Experimental results indicate that the proposed method can successfully detect the periodic impact features from the low signal-to-noise ratio (SNR) signal. Furthermore, in the processing of the early fault vibration signals of the ball bearings, the proposed method can be adopted to obtain the impulse feature frequencies effectively, which is used to diagnose the early fault of ball bearings.
Key words:ball bearing; feature detection; early fault; Morlet wavelet; shuffled frog leaping algorithm
DOI:10.3969/j.issn.1001-0505.2016.03.001
收稿日期:2015-09-26.
作者简介:张菀(1989—),女,博士生;贾民平(联系人),男,博士,教授,博士生导师,mpjia@seu.edu.cn.
基金项目:国家自然科学基金资助项目 (51075070)、高等学校博士学科点专项科研基金资助项目(20130092110003).
引用本文: 张菀,贾民平,朱林.一种自适应Morlet小波滤波方法及其在滚动轴承早期故障特征提取中的应用[J].东南大学学报(自然科学版),2016,46(3):457-463. DOI:10.3969/j.issn.1001-0505.2016.03.001.
