基于灵敏度和特异度任意赋权的加权比数积*
2016-06-24南方医科大学生物统计学系510515李丹玲段重阳邓居敏陈平雁
南方医科大学生物统计学系(510515) 李丹玲 段重阳 邓居敏 陈平雁
基于灵敏度和特异度任意赋权的加权比数积*
南方医科大学生物统计学系(510515) 李丹玲 段重阳 邓居敏 陈平雁△
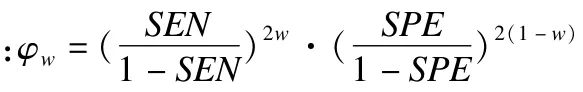
【关键词】加权比数积 权重 灵敏度 特异度
*国家自然科学基金项目(81273191,81402759);全国统计科学研究计划项目(2013LY059);广东省医学科研基金(B2013222)资助;广东省自然科学基金(2015A030310279)
自Yerushalmy(1947)[1]提出灵敏度(sensitivity,SEN)和特异度(specificity,SPE)以来,它们一直是评价诊断试验最基本和最重要的两项指标。然而在不同诊断方法进行比较时,一者的灵敏度较高而另一者的特异度较高时,难以对其做出综合评价。于是结合灵敏度和特异度的综合评价指标由此产生,如Youden指数[2-3]、标准化诊断符合率[4]、比数积[5-8]。然而,当灵敏度和特异度的重要性不同时,此类综合评价指标不能反映诊断的真实价值[6]。为此,我们之前的研究已经建立了基于灵敏度与特异度任意赋权的加权Youden指数[9]以及广义加权标准化诊断符合率[10]。比数积方法先后由陈平雁[5]和Glas[8]独立提出,目前在诊断试验评价领域有广泛应用,但其加权方法尚未产生。因此,本研究将建立一种新的诊断试验评价指标加权比数积。
加权比数积的构建
诊断试验的结果如表1,纵标目是以“金标准”(gold standard)或称参照标准(reference standard)确诊的受试个体属于“患者”(D +)或“非患者”(D-);横标目为诊断方法所判定的结果“阳性”(T +)或“阴性”(T-)。

表1 某方法诊断某病种的结果(例数)
其中灵敏度与特异度的定义如下:
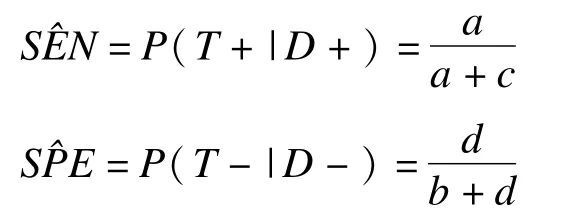
比数积的直观意义很明显,即比数积愈大,诊断的准确性愈高,诊断试验的效果愈好。
对φ取对数,易求得lnφ的近似方差,
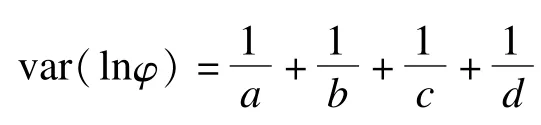
假设有两个相互独立φ1和φ2,欲检验H0:φ1=φ2(两样本的比数积来自同一总体)是否成立。在H0下,根据中心极限定理,当两样本量均较大时,无论φ服从何种分布,总有
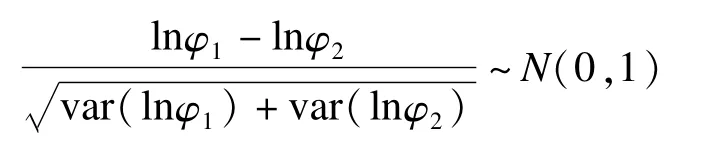
从而可构建检验比数积的统计量Z,
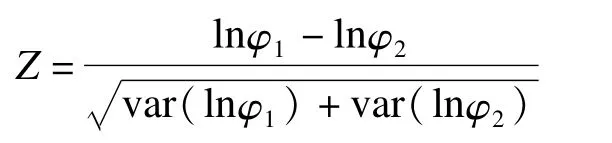
其中
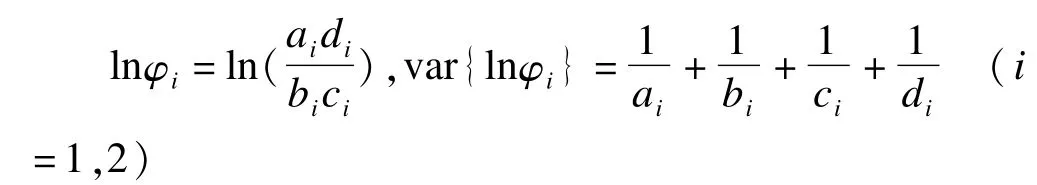
由上面推导可见,比数积检验不受病例组构成的限制,克服了Youden指数的缺陷,且在计算上较标化诊断符合率检验简单。但应注意,比数积检验要求四格表内的数均不为0。
加权比数积φw的构造满足以下三个原则:灵敏度和特异度的权重(w)之和为1,0≤w≤1;满足特殊性:当灵敏度和特异度等权时,即w =0.5时,加权比数积φw等于比数积φ;加权比数积φw的取值范围与比数积φ的取值范围相同,为[0,+∞]。所构造的加权比数积为:
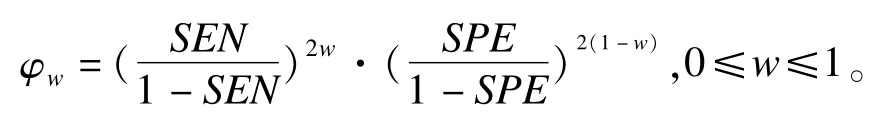
加权比数积的统计推断
将φw取对数:
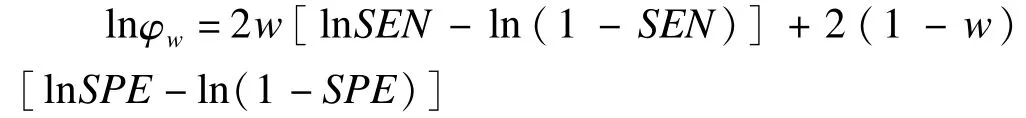
用Delta法求方差:
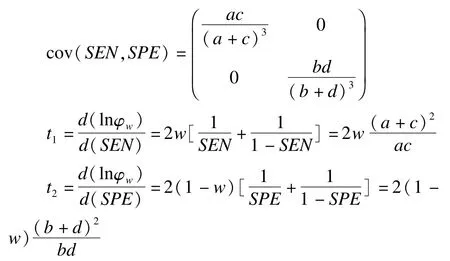
从而得lnφw的近似方差:
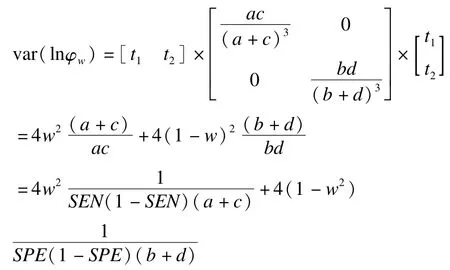
所构造的检验统计量为:

样本量较大时,Z近似服从标准正态分布。
实 例
血浆中的肾上腺素(A试验)和尿中肾上腺素联合去甲肾上腺素(B试验)可用于诊断嗜铬细胞瘤[11],结果见表2。A诊断试验的对象是20例嗜铬细胞瘤确诊病人以及62例对照,其灵敏度与特异度分别为40%和88.7%,B诊断试验的对象是15例病人以及53例对照,灵敏度与特异度分别为93.3%和58.5%,为比较A诊断试验与B诊断试验的临床诊断价值,我们在权重为0.3,0.5,0.8三种情况下分别计算两者的加权比数积与相应的检验统计量Z,结果见表2。

表2 诊断嗜铬细胞瘤的结果
当灵敏度与特异度赋以相同的权重(即同等重要),此时的加权比数积与比数积是相等的。A试验与B试验的加权比数积φw分别为5.233(95%CI 1.591 ~17.217)和19.630(95%CI 2.406-160.160),差异没有统计学意义(Z =-1.074,P =0.282)。当灵敏度的权重为0.3(特异度的权重为0.7),加权比数积的值分别为14.032与7.853,差异没有统计学意义(Z =0.603,P =0.546)。当灵敏度的权重为0.8,这两个诊断试验的φw分别为1.192与77.577,B试验的加权比数积显著高于A试验(Z =-2.296,P =0.022)。
检验统计量Z为权重w的单调函数
笔者通过理论证明得知权重w对Z的影响如下:
(1)若SEN1≤SEN2,SPE1≥SPE2,则随着w的增大,Z减小(当且仅当SEN1=SEN2,SPE1=SPE2时,Z≡0);
(2)若SEN1<SEN2,SPE1<SPE2,则随着w的增大,Z先减小后增大,最小值点为

(3)若SEN1≥SEN2,SPE1≤SPE2,则随着w的增大,Z增大;
(4)若SEN1>SEN2,SPE1>SPE2,则随着w的增大,Z先增大后减小,最大值点w0同上。
我们通过举例来演示上述四种不同情况下Z如何随w的变化而变化(见图1)。其中甲试验样本量为124,乙试验样本量为154,甲试验病例占比为0.6,乙试验病例占比为0.195
结 论
诊断试验设计中的非平衡性始终是各类综合性指标需要考虑的一个重要问题,加权比数积亦存在这一问题,见下表3,表4
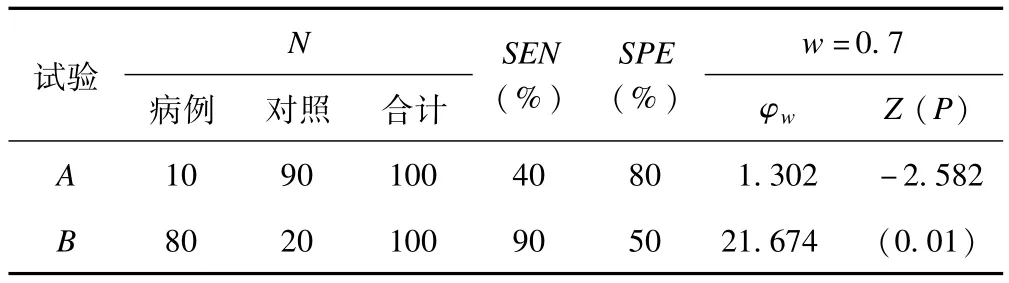
表3 病例占比不同时对加权比数积比较的影响
表3与表4中资料A、B法的灵敏度、特异度与权重均保持不变,若将A组病例占比由表3中的10%变为表4中80%,将B组病例占比由表3中的80%变为表4中10%,病例组占比变化后虽然A法,B法的加权比数积保持不变,可是比较结果却由原来的有显著性差异(P =0.01)变成无显著性差异(P =0.07),可见病例组占比对加权比数积比较的影响是不容忽视的。本文后续工作可探讨不同权重、病例占比、病例占比的差值以及灵敏度与特异度大小关系等参数情况下的Ⅰ类错误以及检验效能的进行比较,为临床工作者在实际应用中提供依据。
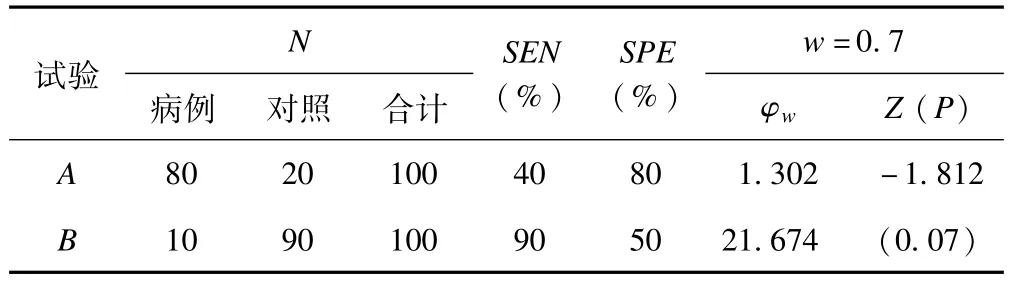
表4 病例占比不同时对加权比数积比较的影响
本文所构建的Z检验统计量,适用于样本量较大的时候,若小样本时或H0成立但检验统计量未知时,若仍按照±1.96的界值计算该指标相应的Ⅰ类错误会偏离事先设定0.05附近,说明此时我们用标准正态分布逼近所构造的检验统计量不准,可采用基于灵敏度与特异度的参数Bootstrap方法调整该指标的界值。
本文所提出两种诊断方法比较的统计推断是基于两个独立样本的比较提出的,如何构建配对诊断试验设计下的加权比数积是接下来有待解决的问题之一。
相对于比数积,加权比数积不仅允许灵敏度和特异度任意赋权,而且更满足特殊性,当灵敏度和特异度等权时(均为0.5),加权比数积等价于比数积。
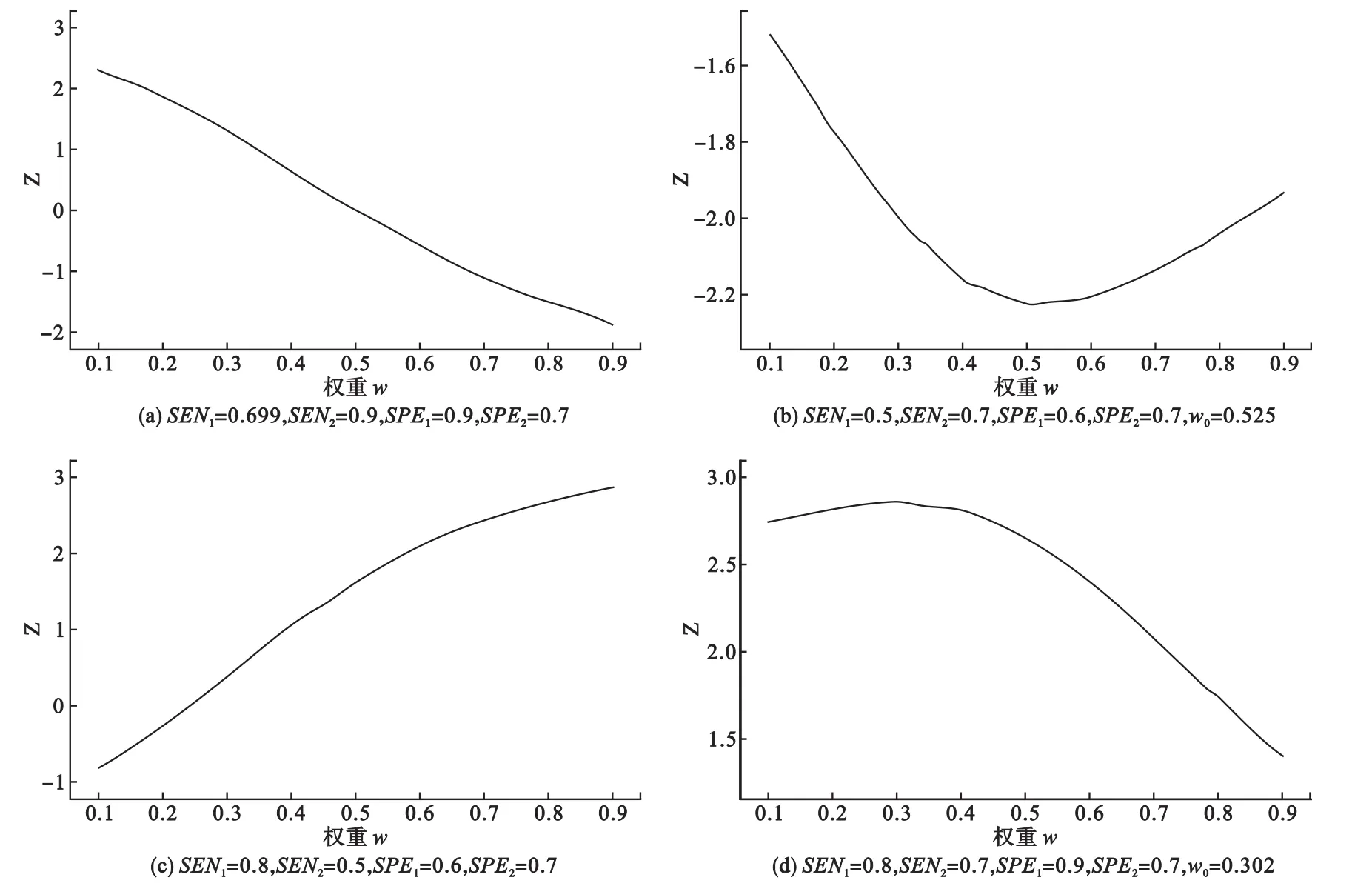
图1 检验统计量Z为权重w的单调函数
本研究根据比数积指标的特性,构建了对灵敏度和特异度的赋权处理,保证了比数积是加权比数积在灵敏度和特异度等权情况下的一种特例,并推导出相应的标准误和两样本比较的统计推断公式,从而建立了一种新的基于灵敏度和特异度任意赋权的评价诊断试验的统计方法,即加权比数积,为诊断试验评价的临床应用提供了更为丰富、实用的工具。
参考文献
[1]Yerushalmy J.Statistical problems in assessing methods of medical diagnosis,with special reference to X-ray techniques.Public Health Reports,1947,62:1432-49.
[2]Youden WJ.Index for rating diagnostic tests.Cancer,1950,3(1):32-35.
[3]Chen F,Xue Y,Tan M,et al.Efficient Statistical Tests to Compare Youden Index:Accounting for Contingency Correlation.Statistics in Medicine,2015,34:1560-1576.
[4]Galen RS,Gambino SR.Beyond Normality:The Predictive Value and Efficiency of Medical Diagnosis.JoneWiley:New York,1975:50-53.
[5]陈平雁,郭祖超,胡琳.比较两种诊断试验的统计方法.中国卫生统计,1990,7(2):22-25.
[6]陈平雁.评价诊断试验的统计指标及其应用.中国卫生统计,1991,8(5):53-57.
[7]陈平雁,王斌会,莫一心.几种诊断试验推断方法的比较.中国卫生统计,1995,12(5):8-11.
[8]Glas AS,Lijmer JG,Prins MH,et al.The diagnostic odds ratio:a single indicator of testperformance.Journal of Clinical Epidemiology,2003,56:1129-1135.
[9]Li D,Shen F,Yin Y,et al.Weighted Youden index and its two-independent-sample comparison based on weighted sensitivity and specificity.Chinese Medical Journal,2013,126(6):1150-1154.
[10]李丹玲,陈平雁.基于灵敏度与特异度任意赋权的广义标准化诊断符合率.中国卫生统计,2012,29(6):794-796.
[11]Unger N,Pitt C,Schmidt IL,et al.Diagnostic value of various biochemical parameters for the diagnosis of pheochromocytoma in patients with adrenal mass.Eur J Endocrinol,2006,154:409-417.
(责任编辑:邓 妍)
Weighted Odds Product Based on Weighted Sensitivity and Specificity
Li Danling,Duan Chongyang,Deng Jumin,et al.(Department of Biostatistics,Southern Medical University(510515),Guangzhou)
【Abstract】Objective To develop a weighted odds product(φw)method for evaluating and comparing diagnostic tests based on weighted sensitivity and specificity.Methods Three principles of constructing weighted odds product φware as follows:firstly,the sum of two weights which are attached to the sensitivity and specificity should equal to 1;secondly,φwequals to φ when the sensitivity and specificity have the same weights.finally the range of possible values of φwis within[0,+∞],which is the same as the odds product φ.Then,the φwis defined by(0≤w≤1) .According to the central-limit theorem,we obtain the standard error of lnφwand propose a statistical inference method to compare two weighted indexes.Furthermore,we also deduce the test statistics Z can be either a monotonously increasing/ decreasing function or non-monotone function of the weight w under different conditions.Results The proposed φwsatisfied the above-mentioned three principles.Conclusion For different weights attached to the sensitivity and specificity,φwcan be used to deal with such kinds of problems as provide a new and practical tool to evaluate diagnostic tests.
【Key words】Weighted odds product;Weights;Sensitivity;Specificity
通信作者:△陈平雁
