反应谱特征周期的统计分析

郭明珠，胡海芹，曹鑫雨，常议彬（北京工业大学城市与重大工程安全减灾共建重点实验室，北京 100124）



反应谱特征周期的统计分析

郭明珠，胡海芹，曹鑫雨，常议彬
（北京工业大学城市与重大工程安全减灾共建重点实验室，北京 100124）

摘 要：反应谱特征周期即反应谱的第二拐点周期，是工程抗震设计的关键参数。收集了美国西部825条强地震记录并进行统计分析，结果表明：（1）反应谱特征周期随着场地的变软，震级的增大而增大，趋势较明显，但是特征周期与震中距和震源深度的线性相关性不明显；（2）竖向特征周期低于水平向特征周期，其差值随着场地的变软而增大；（3）与我国规范相比较，实际统计远场水平特征周期高于我国《建筑抗震设计规范》（GB50011—2010）中的设计特征周期，实际统计竖向特征周期与此规范规定基本相同。该统计分析结果为大型或重要建筑结构抗震设计反应谱确定和抗震设计规范中设计特征周期的确定具有参考价值。

关键词：反应谱特征周期；统计分析；场地条件；震级；震中距；震源深度

0 引言

特征周期是反应谱的重要参数之一，是反应谱的第二拐点周期值，是设计反应谱标准化之后的地震动加速度反应谱平台段的终止周期。特征周期是建筑抗震设计必要参数之一。设计特征周期与地震影响系数是设计反应谱曲线的两个重要参数。在我国历年的抗震设计规范修订中，对设计特征周期和地震影响系数取值一直在不断地修改和完善［1-3］，设计特征周期和地震影响系数取值的变化体现了其在地震动反应谱领域中的重要地位［4］。水运工程抗震设计规范（JTS 146—2012）中特征周期仅考虑了场地类别，公路桥梁和构筑物等抗震设计规范中特征周期均根据场地类别和地震动参数区划图确定；室外给水排水和燃气以及建筑抗震设计规范中特征周期是根据场地类别和地震分组确定的。有学者研究特征周期随着覆盖层厚度的增加而逐渐增大［5］。有学者研究，反应谱特征周期按场地类别和震中距（地震分组）确定，存在不确定的风险［6］。也有学者认为特征周期随着场地的变软而增大，与震级有良好的线性关系，但是与震中距影响不大［7］。本文收集美国西部地区的约825条强震记录进行统计分析，在前人研究了水平特征周期与场地、震级、震中距关系的基础上，本文继续采用不同地震记录研究了场地、震级、震中距和震源深度对水平特征周期的影响，通过多次强震震害研究发现很多结构因竖向地震动而导致破坏［8］，同时研究了四种因素对竖向地震动特征周期的影响。

1 反应谱特征周期的计算方法

各国抗震规范［9-11］给出的特征周期计算方法并不完全相同。我国《建筑抗震设计规范》（GB50011—2010）按场地类别与设计地震分组确定特征周期［9］；欧洲抗震规范EC8是根据土层特征确定的地面分类确定特征周期［11］；美国ATC3-06规定采用地面运动参数：有效峰值加速度EPA和有效峰值速度EPV确定特征周期。反应谱特征周期的计算方法有多种，在此列举几个典型方法：

（1）美国ATC3-06规范法

式中EPA为5%阻尼比时绝对加速度反应谱高频段（0. 1～0. 5s）的平均谱值除以2. 5；

EPV为相应速度反应谱在（0. 5～2. 0s）段的平均谱值除以2. 5。

（2）《中国地震动参数区划图》（GB18306—2001）法

《中国地震动参数区划图》（GB18306—2001）对美国ATC3-06规范进行了修改，首先在对数坐标系中做出拟速度反应谱和绝对加速度反应谱，找出绝对加速度反应谱平台段的起始周期T0和结束周期T1，在拟速度反应谱上选定平台段的起始周期为T1，结束周期为T2。

式中EPA*为［T0，T1］区间绝对加速度反应谱均值除以2. 5；

EPV*为［T1，T2］区间拟速度反应谱均值除以2. 5。

（3）用峰值加速度与峰值速度标定法

式中Samax为加速度反应谱最大值；

Svmax为速度反应谱最大值。

（4）概率法

用平台化的反应谱与初始反应谱的面积比表示，可表达为

式中Ta%为占实际地震反应谱面积a%的设计反应谱特征周期；

Sa%为a%面积比的平台化反应谱曲线；

Tmax（Sa%）为Sa%平台段所对应的最大周期。

本文数据主要来源于美国强震记录数据库COSMOS Virtual Data Center（COSMOS），共收集了约825条美国西部地区的三分量强震记录，并用Matlab处理，由于强震记录均为美国记录，因此采用美国ATC3-06规范法计算特征周期进行统计分析。

2 强震记录的选取

美国西部地震属于板内地震构造，与中国大陆地震构造相似，因此，研究美国西部的强震记录特性对中国大陆工程抗震有很强的借鉴意义［12］。本文收集了美国西部111个台站的地震记录，经筛选确定了较完整的825条地震记录，包含水平地震及竖向地震记录。

美国ATC3- 06主要是根据V30等效剪切波速确定场地类别。A：V30＞1500m/ s；B：760m/ s＜V30≤1500m/；C：360m/ s＜V30≤760m/ s；D：180m/ s＜V30≤360m/ s；E：V30≤180m/ s；F：其他条件。在软岩和土层场地还考虑了标贯抗力和不排水抗剪强度2个指标，而我国抗震规范是按20m以内等效剪切波速和波速在500m/ s以上的硬土深度来确定场地类别。为了与我国抗震规范保持一致性，根据周锡元院士指出的近似换算公式［13］，换算过程及结果如下：

场地分类按上式计算的等效剪切波速范围为：Ⅰ类场地：V30＞500m/ s，Ⅱ类场地：260m/ s＜V30≤500m/ s，Ⅲ类场地：150m/ s＜V30≤260m/ s，Ⅳ类场地：V30≤150m/ s。本文统计的地震记录分布在Ⅰ、Ⅱ、Ⅲ类场地。

强震记录按照场地类别、震级、震中距和震源深度4个因素分类。场地类别按照我国规范涵盖Ⅰ类场地、Ⅱ类场地和Ⅲ类场地。震级M划分为3个区间，分别是4≤M1＜5. 5，5. 5≤M2＜6. 5和6. 5≤M3＜8；震中距R（km）分4个区间：0＜R1＜30，30≤R2＜60，60≤R3＜90和90≤R4＜160；震源深度D（km）分3个区间：0＜D1＜6，6≤D2＜12，12≤D3＜30。本文所选用记录均为COSMOS中已处理的记录，地震记录的基本信息及数量如表1所示，分布情况如表2。

由于场地类别及台站分布的不均匀性，强震记录数量关于震级、震中距和震源深度的有限性，数据库的强震记录难以严格满足各因素均匀分布。本文建立的强震数据库大震级上的记录分布较少，但在各场地类别上分布相对较均匀，其他震级段在场地类别和震中距分档上分布较均匀。数据库中Ⅱ类场地地震记录相对Ⅰ类场地和Ⅲ类场地较多，这也符合我国场地类别的分布特点。

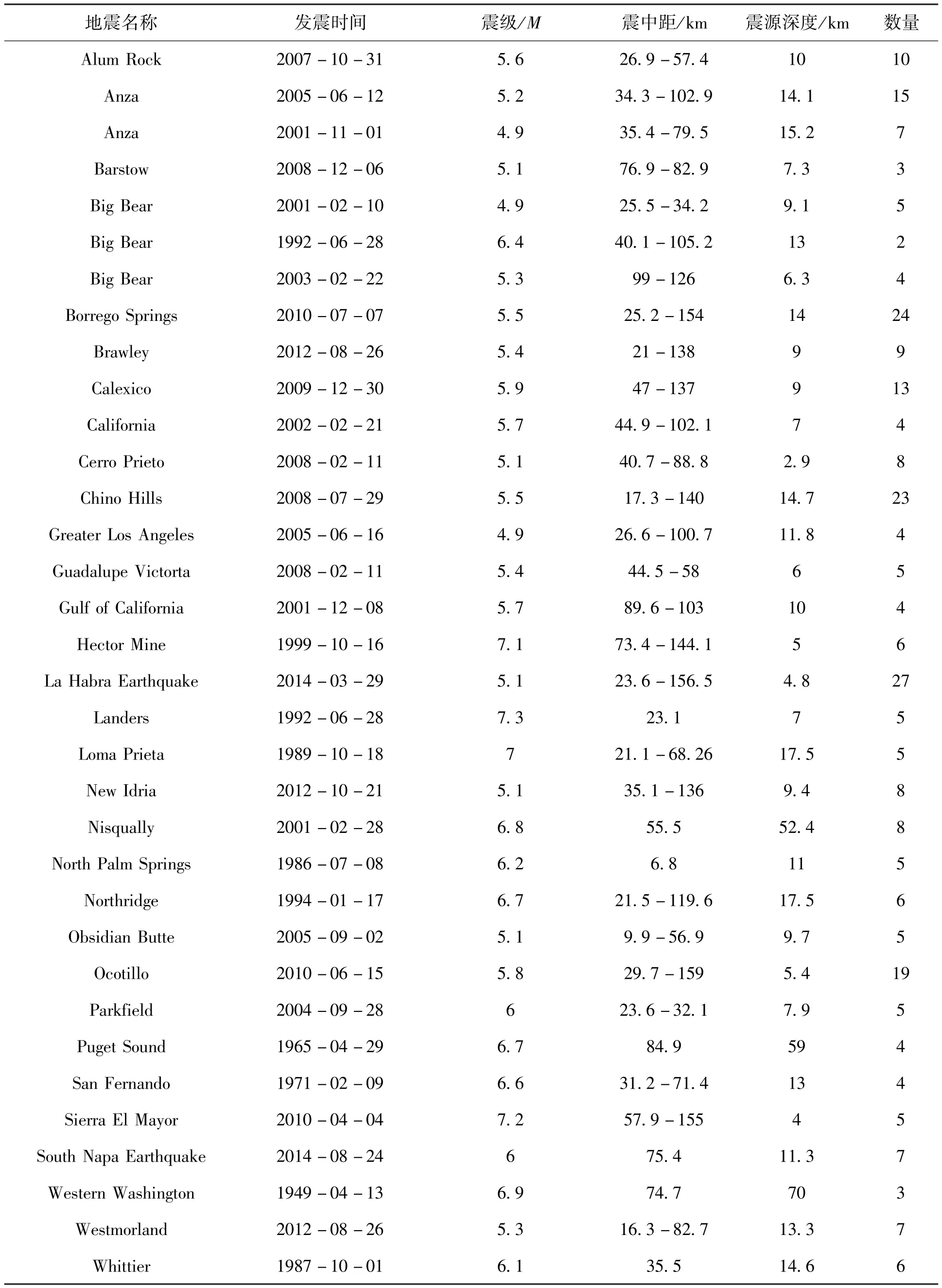
表1　地震记录的基本信息及数量Tab. 1 The basic information and quantity of the seismic records

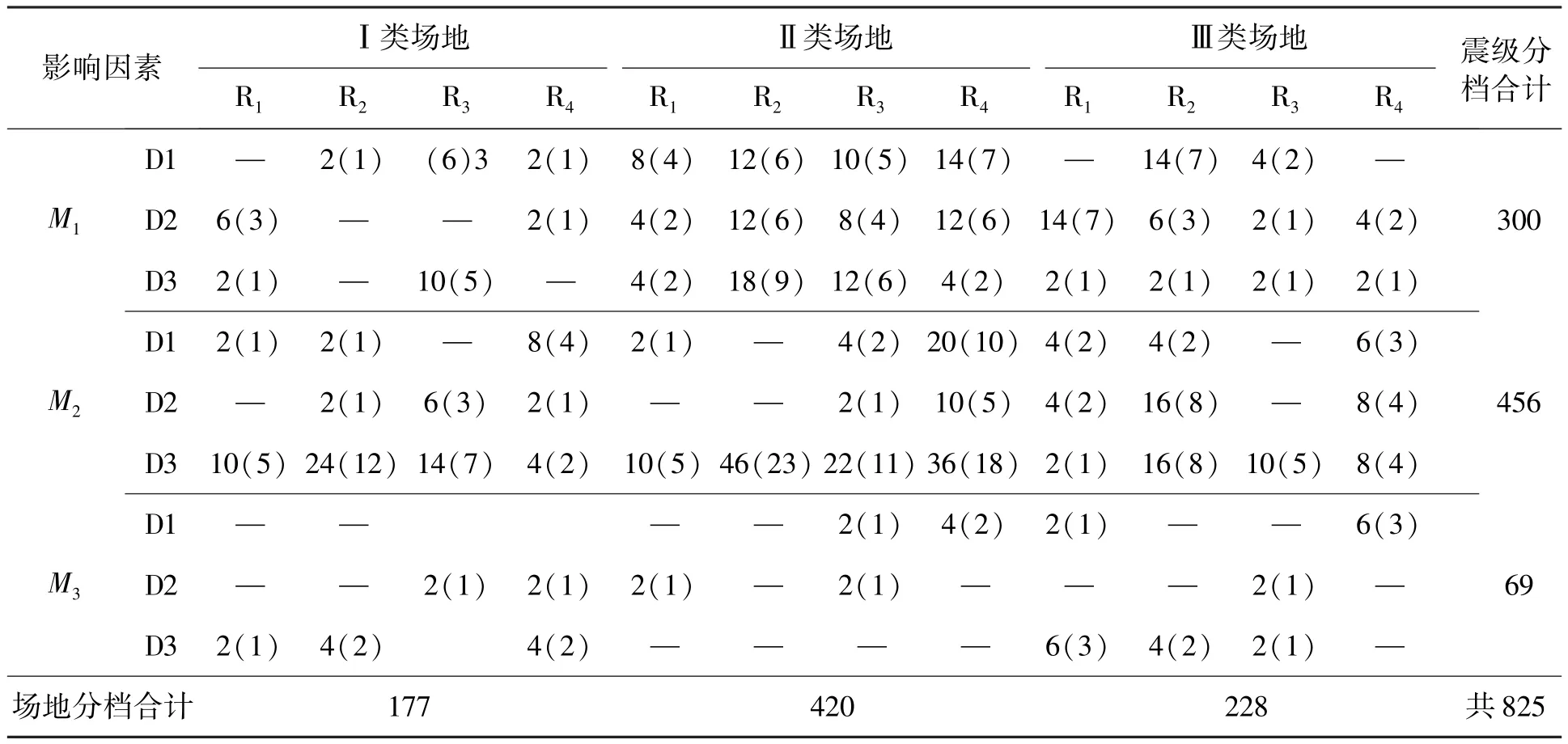
表2　本文所用地震记录分布表Tab. 2 The table of the seismic record distribution table in this paper

3 场地特征周期的影响因素分析

3. 1 场地类别对特征周期的影响分析

我国《建筑抗震设计规范》（GB50011-2010）将场地按照等效剪切波速和覆盖层厚度分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个大类，又将Ⅰ类分为Ⅰ0和Ⅰ1两类。本文收集的美国西部强震记录，对应我国场地类别划分中的Ⅰ、Ⅱ、Ⅲ类场地。不同场地上竖向及水平地震的加速度反应谱特征周期的分布情况如图1所示。

由图1可以看出Ⅰ类场地竖向地震反应谱的特征周期分布在0. 10s～0. 60s之间，主要分布在0. 10s～0. 50s之间，水平向地震的特征周期分布在0. 10s～0. 70s之间，主要分布在0. 10s～0. 60s之间；Ⅱ类场地竖向地震的特征周期分布在0. 05s～1. 75s之间，主要分布在0. 10s～0. 60s之间，水平向地震的特征周期分布在0. 10s～1. 10s之间，主要分布在0. 10s～0. 80s之间；Ⅲ类场地竖向地震的特征周期分布在0. 10s～0. 95s之间，主要分布在0. 15s～0. 75s之间，水平向地震的特征周期分布在0. 25s～1. 25s之间，主要分布在0. 15s～0. 90s之间。随着场地的变软，无论是竖向还是水平向地震反应谱的特征周期都有变大的趋势，而且竖向反应谱特征周期偏小于水平向特征周期。

从表3各类场地特征周期的均值可以明显看出，Ⅰ、Ⅱ、Ⅲ类场地的特征周期在逐渐增大，也就是说，随着场地类别的增大，即场地的变软，地震动反应谱特征周期逐渐增大。Ⅱ类场地的变异系数比Ⅰ类和Ⅲ类场地的大，说明Ⅱ类场地反应谱特征周期离散性相对较大。而且竖向比水平向地震动反应谱特征周期明显偏小。我国GB50011—2010建筑抗震规范规定竖向特征周期Tg按水平设计第一组采用，即Ⅰ类场地竖向特征周期取0. 25s；Ⅱ类场地取0. 35s；Ⅲ类场地取0. 45s。与表2所得的结果相比，Ⅰ类场地比规范偏高0. 04s，Ⅱ类场地比规范偏低0. 06s，Ⅲ类场地比规范偏低0. 04s。

分布图及统计结果均显示，场地越软，反应谱特征周期越大。竖向反应谱特征周期比水平向的明显偏小。统计规律与抗震设计规范中特征周期关于场地的规律基本符合。但三类场地的特征周期分布重复部分较多，这可能与场地分类标准及特征周期计算误差有一定的关系，而且规范中相邻场地的第一组和第三组特征周期取值一样，统计结果与规范也有较好的一致性。

3. 2 震级对特征周期的影响统计分析

震级也是影响特征周期取值的重要因素之一，本文按强震震级分档统计特征周期如图2和图3所示。

由图2震级分布情况及趋势线均可以看出竖向及水平向地震动反应谱特征周期均随着震级的增大而增大，且竖向特征周期随震级变化的趋势线斜率相对较小，表明竖向反应谱特征周期受震级影响相对较小。

由图3更可以直观的发现竖向和水平向特征周期均随着震级的增大而增大，但竖向反应谱特征周期受震级影响相对较小。相应场地上的竖向特征周期均低于水平向的，且随场地变软，二者差值增大。也可以发现竖向和水平向特征周期均随场地的变软而变大。Ⅰ类场地和Ⅱ类场地变化趋势基本相同，但Ⅲ类场地从［5. 5，7）到［7，8）震级档突然变陡，说明Ⅲ类场地发生大震级地震时地震动特征周期比较大，这可能是由Ⅲ类场地的软土对地震动的放大作用引起的。

3. 3 震中距对特征周期的影响统计分析

本文将强震震中距分为四个区段对特征周期进行统计分析如图4和图5所示。由图4中的趋势线可以看出反应谱特征周期随着震中距的增大而增大，但斜率较小，线性趋势线相对较平缓，说明震中距对特征周期影响不大。而且水平向反应谱特征周期明显大于竖向特征周期。综合发现震中距对竖向和水平向特征周期影响程度相当。

从图5可以看出特征周期整体上随着震中距的增大略有增大趋势，其中Ⅰ、Ⅱ类场地的［30，60）及Ⅲ类场地的［0，30）档特征周期偏高，影响了整体趋势变化，这一现象的出现可能与数据收集的不均匀有关。图5表明震中距对特征周期影响不是很大。从图中不难发现随着场地类别的增大，即随着场地的变软，竖向与水平向特征周期差值在不断增大。

从图4不难发现地震动反应谱特征周期随震中距的增大有略增大趋势；但图5中此规律并不明显，说明震中距对特征周期影响不大。

3. 4 震源深度对特征周期的影响统计分析

本文将强震震源深度（km）分为三个区段进行统计分析，特征周期分布规律如图6和图7所示。

由图6可以看出反应谱特征周期随着震源深度的变化并不明显，线性趋势线很平缓，说明震源深度对特征周期影响不大。

从图7可以看出特征周期整体上随着震源深度的增大而略有增大，且趋势很平缓。在图6和图7中均显示出特征周期与震源深度略显正比关系，但震源深度对特征周期影响不大。

4 特征周期影响因素综合分析

4. 1 水平向特征周期

前面分别分析了场地与震级、震中距和震源深度双因素对地震动反应谱特征周期的影响，现将四种影响因素综合统计分析列于表4。

从表4可以看出，场地和震级对特征周期影响较大，特征周期随着场地变软，震级增大而不断增大，趋势明显。而震中距和震源深度对其影响不大，这与前面双因素分析结果有较好的一致性。

分析可知特征周期的离散性较大，但其影响因素的趋势性对抗震设计规范中特征周期的取值研究意义也相当大。我国《建筑抗震设计规范》（GB50011—2010）中特征周期的取值根据场地类别和设计地震分组确定。本文综合考虑震级、震中距和震源深度参照我国抗震规范中的设计地震分组对本文统计的地震记录进行分组，将各场地类别震中距在0≤R＜50分档区间的所有震级、震源深度范围内的特征周期值取平均作为第一组，将各场地类别震中距在50≤R＜100分档区间的所有震级、震源深度范围内的特征周期值取平均作为第二组，将各场地类别震中距在100≤R＜160分档区间的所有震级、震源深度范围内的特征周期值取平均作为第三组，按照这种分组方法对统计的美国西部地区的强震记录进行分组列于表5，不难发现将震中距分为三组情况下，可以明确显现出特征周期随震中距的增大而增大的趋势，这与前面3. 3震中距对特征周期的影响统计分析结果并不矛盾，而可能是恰好震中距在30到50之间的记录震级较大造成的。且有学者通过芦山地震研究发现远场台站中长周期成分较为卓越［14］，表5所得规律与芦山地震特征周期规律一致。

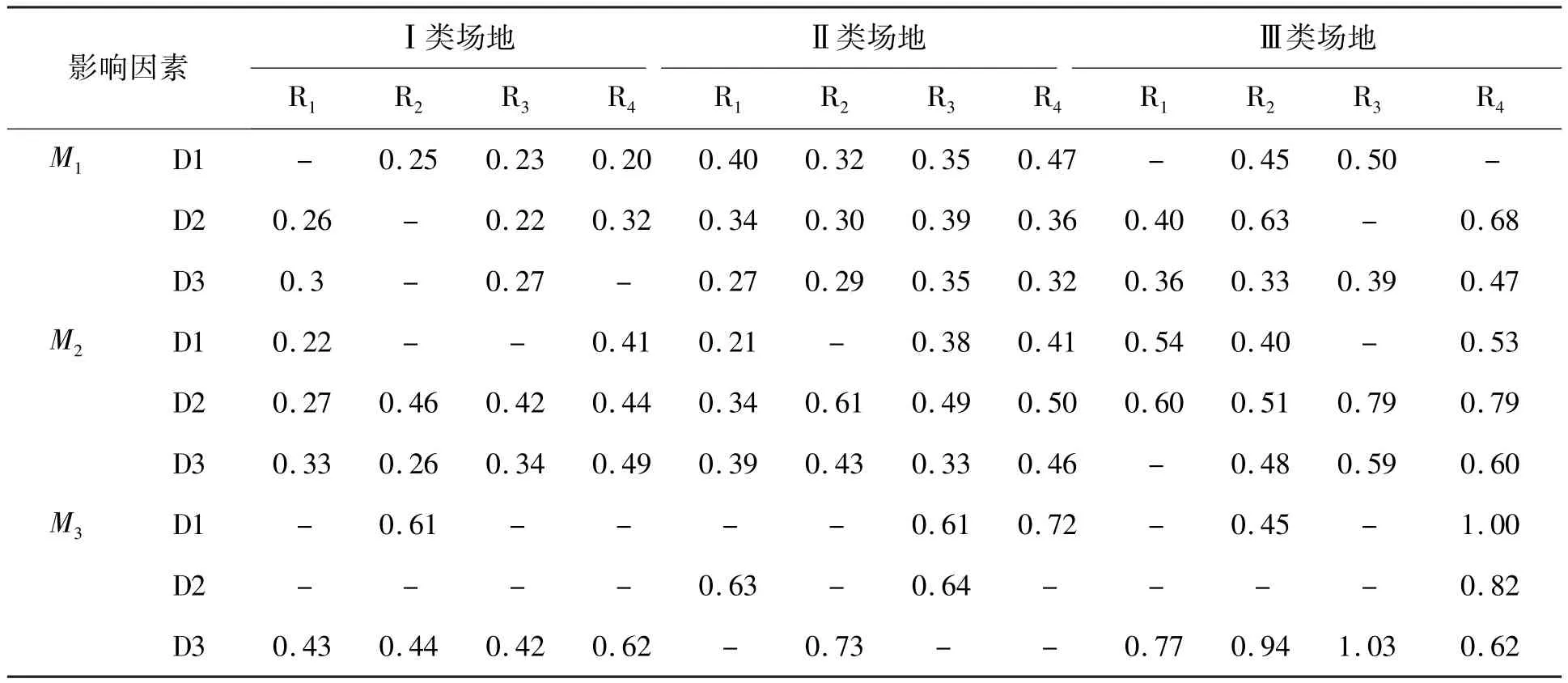
表4 四种影响因素综合分析的特征周期值（s）Tab. 4 The characteristic periods of response spectra comprehensively analyzed by four factors（s）

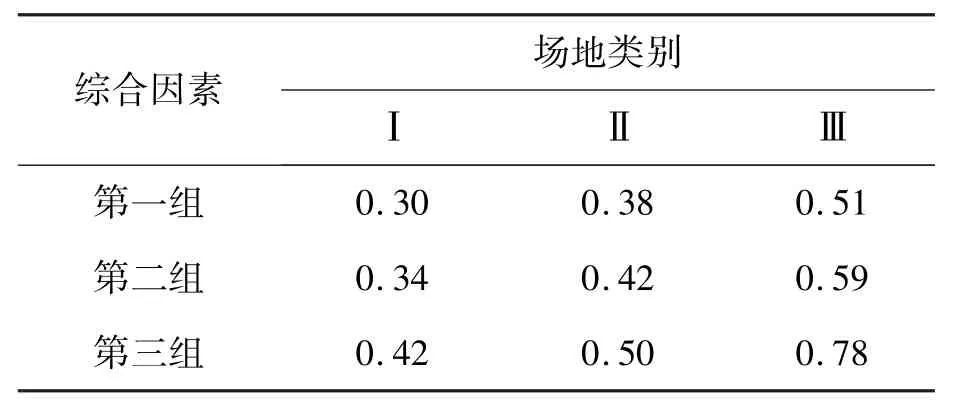
表5 综合因素作用下的特征周期均值表（s）Tab. 5 The average values of characteristic periods of response spectra under comprehensive factors

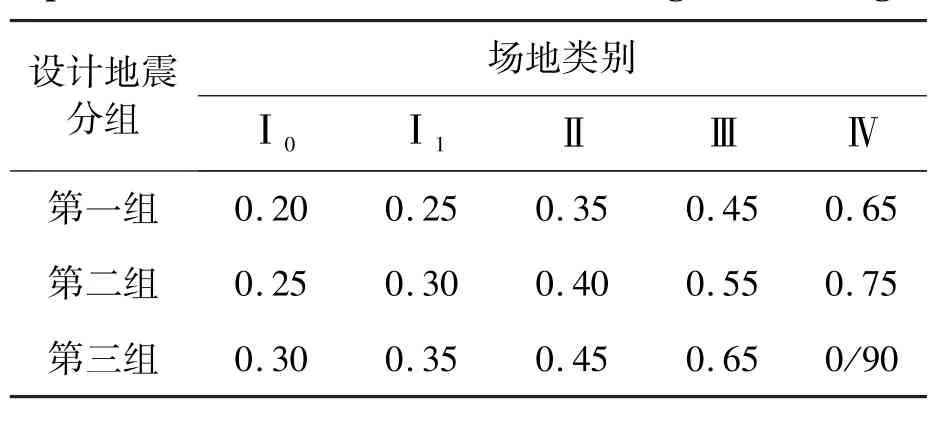
表6 我国抗震设计规范中特征周期取值（s）Tab. 6 Values of characteristic periods of response spectra in Chinese code for seismic design of buildings

我国建筑抗震设计规范对Ⅰ类场地细分为Ⅰ0和Ⅰ1两类场地，其中Ⅰ0类为基岩场地，Ⅰ1类为除基岩以外的Ⅰ类场地，本文将基岩也划分在Ⅰ类场地中。对比表5和表6可以发现：（1）我国建筑抗震设计规范中Ⅰ0类和Ⅰ1类场地三组特征周期的平均取值均低于实际统计计算值，差值分别为0. 07s，0. 06s和0. 09s；（2）Ⅱ类场地第一组和第二组特征周期取值略低于实际统计计算值；而第三组低于实际统计计算值0. 05s；（3）Ⅲ类场地第一组和第二组分别低于实际统计计算值0. 06s和0. 04s，第三组远小于实际统计计算值，差值为0. 13s。

由于数据统计的误差可能会导致实际计算结果与建筑抗震设计规范存在一定的偏差，但是整体上我国建筑抗震设计规范特征周期取值比实际值偏低。

4. 2 竖向特征周期

我国《建筑抗震设计规范》（GB50011—2010）规定竖向特征周期Tg按水平设计第一组采用，即Ⅰ类场地竖向特征周期取0. 25s；Ⅱ类场地竖向特征周期取0. 35s；Ⅲ类场地竖向特征周期取0. 45s。现将本文统计的竖向特征周期按照场地类别和震级分组统计结果列于表7。

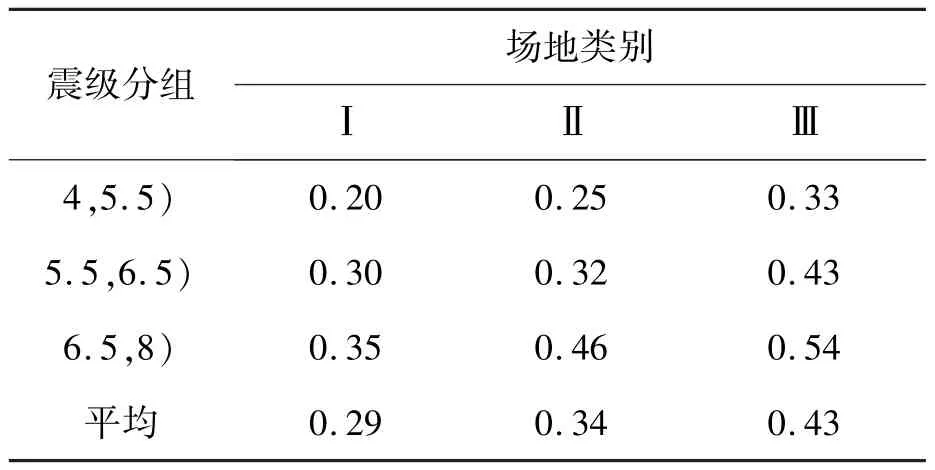
表7　竖向特征周期统计结果（s）Tab. 7 The results of vertical characteristics periods of response spectra

由表6可知，三种类场地所有震级的特征周期的平均值分别为0. 29s、0. 34s和0. 43s，这与建筑抗震设计规范规定基本相同。

5 结语

本文以美国西部地区的强震记录为基础，分别从双因素和综合因素两方面，统计分析了场地、震级、震中距和震源深度四因素对地震动反应谱特征周期的影响。统计分析结果显示：

（1）特征周期随着场地的变软而增大，随震级的增大而增大，趋势明显；

（2）随震中距和震源深度的增大略显增大，趋势不明显；

（3）竖向地震动特征周期的取值低与水平向地震动的特征周期，且随着场地的变软，二者差值不断增大。

（4）我国建筑抗震设计规范水平向特征周期取值比实际值偏低，而竖向特征周期取值与实际值基本相同。

本文统计结果希望能对抗震设计规范关于特征周期的修正有所帮助。

参考文献

［1］ 周锡元，樊水荣，苏经宇.场地分类和设计反应谱的特征周期—《建筑抗震设计规范》修订简介（八）［J］.工程抗震，1999，（4）：3-8.

［2］ 陈国兴.中国建筑抗震设计规范的演变与展望［J］.防灾减灾工程学报，2003，23（1）：102-113.

［3］ 赵艳，郭明珠，吴焕娟，等.关于改进我国抗震设计反应谱的探讨［J］.地震工程与工程振动，2006，26（3）：47-50.

［4］ 徐龙军.统一抗震设计谱理论及其应用［R］.哈尔滨：哈尔滨工业大学图书馆，2006（2）：191-199.

［5］ 梁久亮，曹均锋，王立会，等.滁州地区覆盖层厚度对场地地震动参数的影响［J］.防灾科技学院学报，2015，17（1）：40-46.

［6］ 刘文峰，付兴潘，于振兴，等.反应谱特征周期的统计分析［J］.青岛理工大学学报，2009，30（5）：1-7.

［7］ 夏蕊芳，闫帅平，冯程程.设计特征周期的影响因素［J］.土木工程与管理学报，2012，29（2）：99-102.

［8］ 徐龙军，谢礼立.竖向地震动加速度反应谱特性［J］.地震工程与工程振动，2007，27（6）：17-23.

［9］ GB50011—2010，建筑抗震设计规范［S］.

［10］ IBC International Building Code［S］. International Code Council，2006.

［11］ EC8（2004）. Eurocode 8：Design of Structures for Earthquake Resistance. Part1：General Rules，Seismic Actions and Rules f or Buildings［S］. London：British Standards Institution，EC8，EN1998- 1：2004.

［12］ 郭恩，郭永刚.场地类别划分与抗震设计反应谱的研究［J］.山西建筑，2009，（33）：16-17.

［13］ 周锡元，王国权，杨润林，等. 1999年9月21日台湾集集地震中不同场地上峰值加速度的衰减规律［C］/ /编委会编.大型复杂结构的关键科学问题及设计理论研究论文集.哈尔滨：哈尔滨工业大学出版社，2002：406-413.

［14］ 任叶飞，温瑞智，周宝峰，等. 2013年4月20日四川芦山地震强地面运动三要素特征分析［J］.地球物理学报，2014，57（6）：1836-1846.

Statistical Analysis of Characteristic Period of Response Spectrum

Guo Mingzhu，Hu Haiqin，Cao xinyu，Cang Yibin
（The Key Laboratory of Urban Security and Disaster Engineering，Ministry of Education，Beijing University of Technology，Beijing 100124，China）

Abstract：Characteristic period of response spectrum is an important characteristic parameter for engineering seismic design，it is also the second turning point period of response spectrum. This paper has collected 825 strong earthquake records in western United States and has carried on the statistical analysis. The analysis results indicate that（1）the characteristic period of response spectrum increases when the site becomes soft or when the magnitude increases，the trend is more obvious；But the linear relation of characteristic period of response spectrum with the epicenter distance and focal depth are not obvious.（2）The vertical characteristic period is lower than the horizontal characteristic period，and the difference value increases with the site becoming softer.（3）Compared with the Chinese code，the actual statistical horizontal characteristic period which is far from the fault is higher than the provided value by Code for Seismic Design of Buildings（GB50011—2010）in China：The actual statistical vertical characteristic period and the provided value in Chinese code are basically the same. The statistical analysis results in this paper have a reference value for determining characteristic period of response spectrum for large or important building structure and Code for Seismic Design of Buildings.

Keywords：characteristic period of response spectrum；statistical analysis；site condition；magnitude；epicenter distance；focal depth

中图分类号：P315. 9

文献标识码：A

文章编号：1673-8047（2016）01-0042-09

收稿日期：2016-01-06

基金项目：国家自然科学基金（51278017）

作者简介：郭明珠（1963—），男，博士，教授，主要从事工程地震和强震观测方面的工作。