三次曲线过定点的切线有几条?
2016-06-23安徽省太和中学
安徽省太和中学 岳 峻
三次曲线过定点的切线有几条?
安徽省太和中学岳 峻

一、问题的提出
引例(2014年北京卷)已知函数f(x)=2x3-3x。
(1)求f(x)在区间[-2,1]上的最大值。
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围。
(3)过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
本题第(2)(3)问都是“过一点作三次函数图像切线的条数”的问题,且第(3)问只需写出结论,如何才能迅速地进行判断呢?有没有规律性的结论呢?
二、直线与曲线相切的概念
如图1,设曲线C是函数y=f(x)的图像,在曲线C上取点P(x0,y0)及与P邻近的点Q(x0+Δx,y0+Δy),过P、Q两点作割线,并分别过P、Q两点作x轴、y轴的平行线MP、MQ,又设割线PQ的倾斜角为β,那么MP=Δx,MQ=Δy。这就是说,就是割线的斜率。
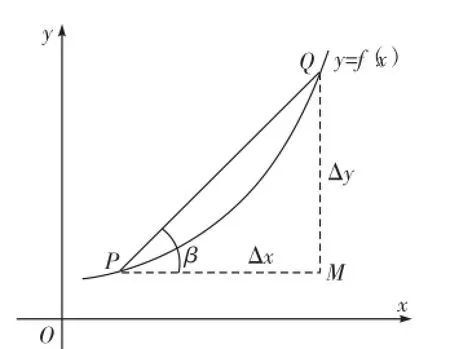
图1
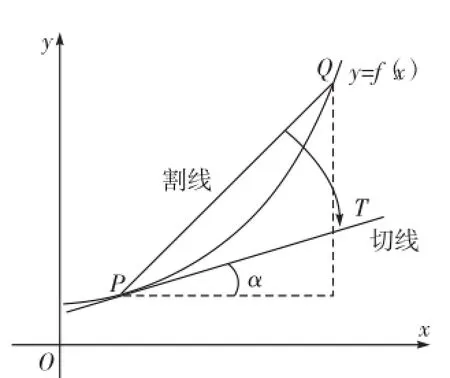
图2
如图2,当点Q(x0+Δx,y0+Δy)沿着曲线逐渐向点P(x0,y0)接近时,割线PQ将绕着点P逐渐转动。当点Q沿着曲线无限接近点P,即Δx→0时,割线PQ有一个极限位置PT,那么,直线PT叫作曲线在点P处的切线。
由直线与曲线相切的概念可知,切线是割线的极限位置,直线与曲线相切是一个局部的概念,因而直线l与曲线C可以同时相切于点A并相交于点B,比如曲线y=x3与直线y=3x+2在点(-1,-1)处相切,在点(2,8)处相交,如图3。
三、探究
对于函数f(x)=2x3-3x,过定点Q(x0,y0)的直线l与函数y=f(x)的图像相切,这样的直线l有几条?
设直线l与曲线y=f(x)相切于点M(t,f(t)),则切线方程为y-f(t)=f′(t)(x-t),
因为切线必过点Q(x0,y0),则y0-f(t)=f′(t)(x0-t),
所以y0-(2t3-3t)=(6t2-3)(x0-t),整理可得4t3-6x0t2+y0+3x0=0(*)。
显然,关于t的方程(*)有多少个不同的解,就有多少条不同的切线。
下面,我们来解决方程(*)的解的个数问题。
设g(t)=4t3-6x0t2+y0+3x0,则g′(t)=12t2-12x0t=12t(t-x0),
由g′(t)=0,得t1=0,t2=x0,
(1)当x0=0时,g′(t)≥0,g(t)单调递增,方程(*)有1个解。
(2)当x0≠0时,g(t)的两个极值分别为g(0)=y0+3x0,
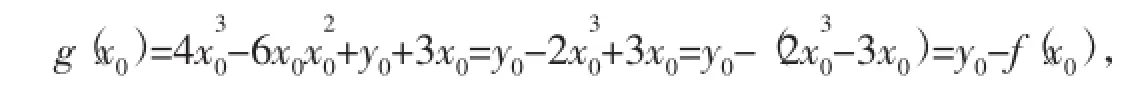
(ⅰ)当g(0)g(x0)>0,即(y0+3x0)[y0-f(x0)]>0时,两个极值同号,定点Q(x0,y0)在不等式(y+ 3x)[y-f(x)]>0所表示的平面区域内,此时,函数g(t)只有1个零点,方程(*)有1个解(注意到函数f(x)=2x3-3x是奇函数,坐标原点是对称中心,等式y+3x=0所表示的直线恰好是曲线y=f(x)在原点处的切线);
(ⅱ)当g(0)g(x0)=0,即(y0+3x0)[y0-f(x0)]=0时,定点Q(x0,y0)在等式(y+3x)[y-f(x)]=0所表示的曲线上,此时,函数g(t)有2个零点,方程(*)有2个解;
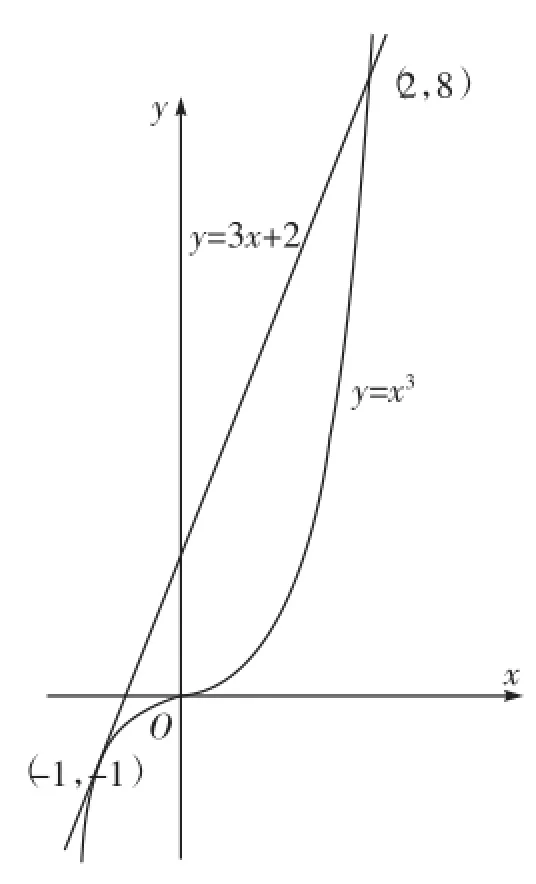
图3
(ⅲ)当g(0)g(x0)<0,即(y0+3x0)[y0-f(x0)]<0时,定点Q(x0,y0)在不等式(y+3x)[y-f(x)]<0所表示的平面区域内,此时,函数g(t)有3个零点,方程(*)有3个解。
综上所述,很容易给出结论。
四、结论
一般的,已知定点Q,三次函数对称中心N处的切线与曲线将平面分成四个平面区域(如图4所示):
(1)若点Q在图像对称中心N处或在Ⅰ、Ⅱ区域内(不含边界),则过定点Q作三次函数图像切线只能作1条;
(2)若点Q在图像对称中心N处的切线上(对称中心除外)或在函数图像上(对称中心除外),则过定点Q作三次函数图像的切线有2条;
(3)若点Q在Ⅲ、Ⅳ区域内(不含边界),则过定点Q作三次函数图像的切线有3条。
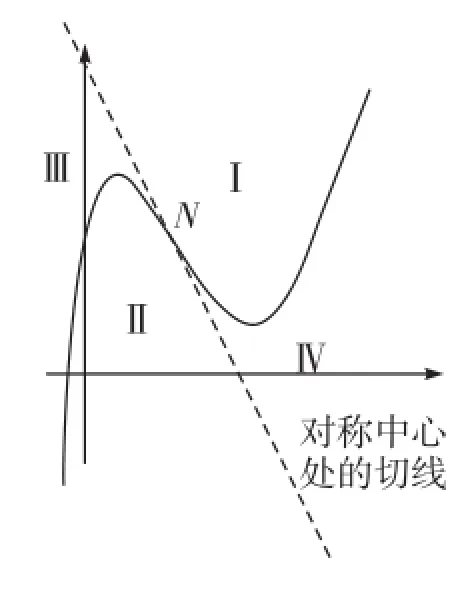
图4
五、应用
对于引例:
已知函数f(x)=2x3-3x。
(1)求f(x)的区间[-2,1]上的最大值。
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围。
(3)过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)解析(1)略。
解析 (1)略。
(2)易知f(1)=-1,f′(0)=-3,又函数f(x)在对称中心处的切线为l0:y=-3x,直线x=1与曲线交于(1,-1),与切线l0交于(1,-3),
因为过点P(1,t)存在3条直线与曲线y=f(x)相切,所以P(1,t)必在区域Ⅳ内,故t∈(-3,-1)。
(3)易知A(-1,2)在区域Ⅲ内,所以过点A(-1,2)存在3条直线与曲线相切;易知B(2,10)在曲线上,且不是对称中心,所以过点B(2,10)存在2条直线与曲线相切;易知C(0,2)在区域Ⅰ内,所以过点C(0,2)存在1条直线与曲线相切。
名师简介
岳峻,安徽省教育学会中学数学教学专业委员会理事,阜阳名师,阜阳市学科带头人。近两年,有30多篇文章分别发表于各类期刊上。
