基于滑模变结构算法的两轮自平衡电动车控制*
2016-06-23蔡志端余庆辉张文莉张银鑫
蔡志端, 余庆辉, 张文莉, 张银鑫, 荀 倩
(湖州师范学院 工学院,浙江 湖州 313000)
基于滑模变结构算法的两轮自平衡电动车控制*
蔡志端,余庆辉,张文莉,张银鑫,荀倩
(湖州师范学院 工学院,浙江 湖州313000)
摘要:针对两轮自平衡电动车(简称两轮自平衡车)平衡控制及其数学模型参数不确定性对系统控制性能影响问题,提出基于滑模变结构和电机磁场定向控制算法的两轮自平衡车控制策略。建立了两轮自平衡车和电机数学模型,并将两轮自平衡系统数学模型进行解耦,得到三个子系统状态空间方程。构造两轮自平衡车控制策略并将滑模变结构算法应用于电机磁场定向控制中。通过仿真分析了所提控制方法的控制效果,表明提出的控制策略可行有效。
关键词:滑模变结构; 两轮自平衡车; 电机
0引言
两轮自平衡电动车(简称两轮自平衡车)是一种电力驱动,具有自我平衡能力的运输载具。其采用电池供电,两轮驱动电机独立控制,具有转弯半径小、能耗低、空间体积小等特点。随着汽车、摩托车等传统交通工具造成的交通拥堵、环境污染等问题,现代的交通工具正朝着智能、小型、节能、环保的趋势发展。两轮自平衡车以其特有的优点逐渐成为一种新型时尚的代步工具,在步行街、大型会场、购物中心、生活住宅小区等机动车辆不便通行的场合得到广泛应用。
两轮自平衡车是建立在 “动态稳定”原理上的一个复杂的非线性系统。以站在车上的驾驶人与车辆的总体重心纵轴作为参考线,根据车身倾角度、转弯角度、速度等姿态信息,应用适当的电机控制算法,控制左右轮驱动电机动作,实现车体的自我动态平衡和稳定的水平行驶线速度。目前平衡车控制策略的研究已成为自动控制领域热点问题。
目前对二轮自平衡车控制策略常用线性控制[1-2],鲁棒控制[3],智能控制[4-6]等方法。文献[1]基于牛顿力学经典分析方法,建立平衡车的数学模型,采用PID控制器对车体运动进行控制并取得一定的效果。然而,由于二轮自平衡车是强耦合的非线性系统,不能建立精确的数学模型,因此 PID 控制算法在该系统应用中具有一定的局限性。文献[2] 基于鲁棒控制方法,将 H∞与卡尔曼滤波方法相结合,设计了状态反馈控制器(LQR),实现了两轮自平衡车的控制。由于PID、LQR等线性控制方法对于非线性系统难以达到满意的控制效果,学者们则将模糊控制、神经网络、遗传算法等智能算法应用于平衡车控制[4-7]。考虑到两轮自平衡车系统数学模型构建时诸多的不确定性和复杂性,文献[4]提出一种分层模糊智能控制方法,通过2个模糊控制器分别对车体的偏移角度和轮的转动速度进行控制,但是该类方法抗干扰性和鲁棒性不是很强。
滑模变结构控制算法具有良好的抗干扰性、鲁棒性等优点,在系统参数或者外部扰动等不确定性存在时都能保持良好的控制性能,适合于两轮自平衡车非线性系统的控制。由于两轮自平衡车的关键在于对驱动电机的控制,对驱动电机控制系统要求高,而永磁同步电机具有起动转矩大、效率高、可靠性高、调速范围宽等优点,因此成为自平衡车的理想驱动电机。电机的磁场定向控制方法由于其快速的转矩响应和高效的控制性能,适合应用于两轮自平衡车的控制中。本文基于两轮自平衡车和永磁同步电机动力学模型,结合永磁同步电机磁场定向控制方法提出一种滑模变结构的两轮自平衡车控制策略。
1两轮自平衡车控制模型
根据文献[7-9] 得到两轮自平衡车数学模型,如式(1)所示。
(1)
设左右车轮半径R=0.106m,左右车轮质量m=0.42kg,左右轮之间的距离D=0.44m,机器人车体质量M=21kg,机器人车体质心到z轴距离L=0.3m,两轮对转轴的转动惯量Jw=0.0024kg·m2,车体对z轴的转动惯量Jδ=0.63 kg·m2,机器人车体质心到z轴的距离L=0.3m,车体对z轴的转动惯量Jp=0.63kg·m2。根据以上相关参数计算,可进一步得到自平衡车状态方程

(2)
为分析方便,运用解耦方式将整个系统分为平衡控制与转向控制两个子系统。设
(3)
式中:Tθ——实现车体平衡时驱动电机输出转矩;
Tδ——实现车体转向时左右驱动电机差速控制所需要的转矩。
将式(3)代入式(2)得

(4)
可以将式(4)解耦成两个独立单输入子系统。一个子系统是式(5)和式(6),分别为车体平衡控制子系统的状态方程和输出方程。
(5)
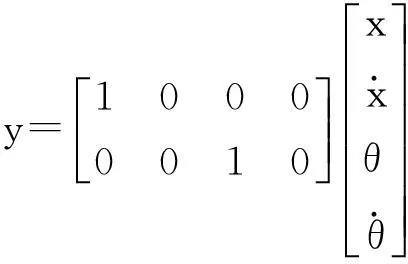
(6)
另一个子系统是式(7)和式(8),为车体转弯控制子系统。
(7)
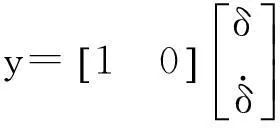
(8)
由以上子系统可知转矩Tθ控制车体水平位移量x和其倾角度θ;转矩Tδ控制车体转弯角度δ。
车体水平行驶线速度与车轮转动角速度关系为
νL=ωLR; νR=ωRR
(9)
式中:νL、νR——左右轮水平行驶线速度;
ωL、ωR——左右车轮机械角速度;
R——车轮半径。
根据车轮角速度和电机极对数,容易计算电机的电角速度值。
永磁同步电机在旋转坐标系下的数学模型[10-11]为
(10)
(11)
Te=np[ψfisq+(Ld-Lq)isdisq]
(12)
(13)
式中:TL——电机负载转矩;
B——电机阻尼系数;
J——电机转动惯量;
ωr——轮子的机械角速度。
式(10)和式(11)为电机电压方程,式(12)为电机转矩方程,式(13)为电机运动方程。
2两轮自平衡车控制策略
2.1系统控制结构

图1 两轮自平衡单个车轮驱动电机控制框图
2.2滑模控制器设计
滑模控制器用于对倾角度、电机水平行驶线速度和电机转弯进行控制。其设计过程主要有切换函数设计和滑模控制律设计两个关键步骤。设各滑模控制器滑模面为
(14)
式中:Sθ——倾角度滑模面;
Sv——线速度滑模面;
Sδ——转角度滑模面。
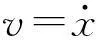
对式(14)求导得
(15)
为获取滑模控制器在其运动阶段良好的动态品质,选取指数趋近律[12-13]:
(16)
式中:ε——切换增益系数,ε>0;
η——指数系数η>0。
创建李亚普诺夫(Lyapunov)函数:
(17)
将式(5)和式(7)代入式(15)并结合 式(16),易得3个滑模控制器各自的控制律为
(18)
(19)
(20)
式中:Teθ——平衡控制所需要的转矩值;
Tev——线性速度需要的转矩值;
Tδ——转弯控制所需要的转矩值。
再根据式(11)及id=0的控制方式,很容易得到各滑模控制器电流控制量。
3仿真
在Simulink仿真平台建立图1所示自平衡车控制程序,分别对上面设计的3个滑模控制器及整个平衡车运动控制进行仿真。 图2~图4分别为平衡控制器、转弯控制器和速度控制器的仿真结果。仿真结果表明,所设计的滑模控制器能较好地跟踪所设置的目标值。图5为车体倾角度、车体倾角角速度和行驶速度变化曲线。图5中,车体前倾时,倾角度为正值,车体开始加速前进,然后倾角和倾角速度通过控制至目标值零,同时车体按指定速度值匀速行驶。当车体后倾时,倾角度为负值,产生刹车或后退效果,然后倾角和倾角速度控制至目标值零,车体行驶速度为零。仿真结果与理论分析一致,说明文献所提方法的正确性。
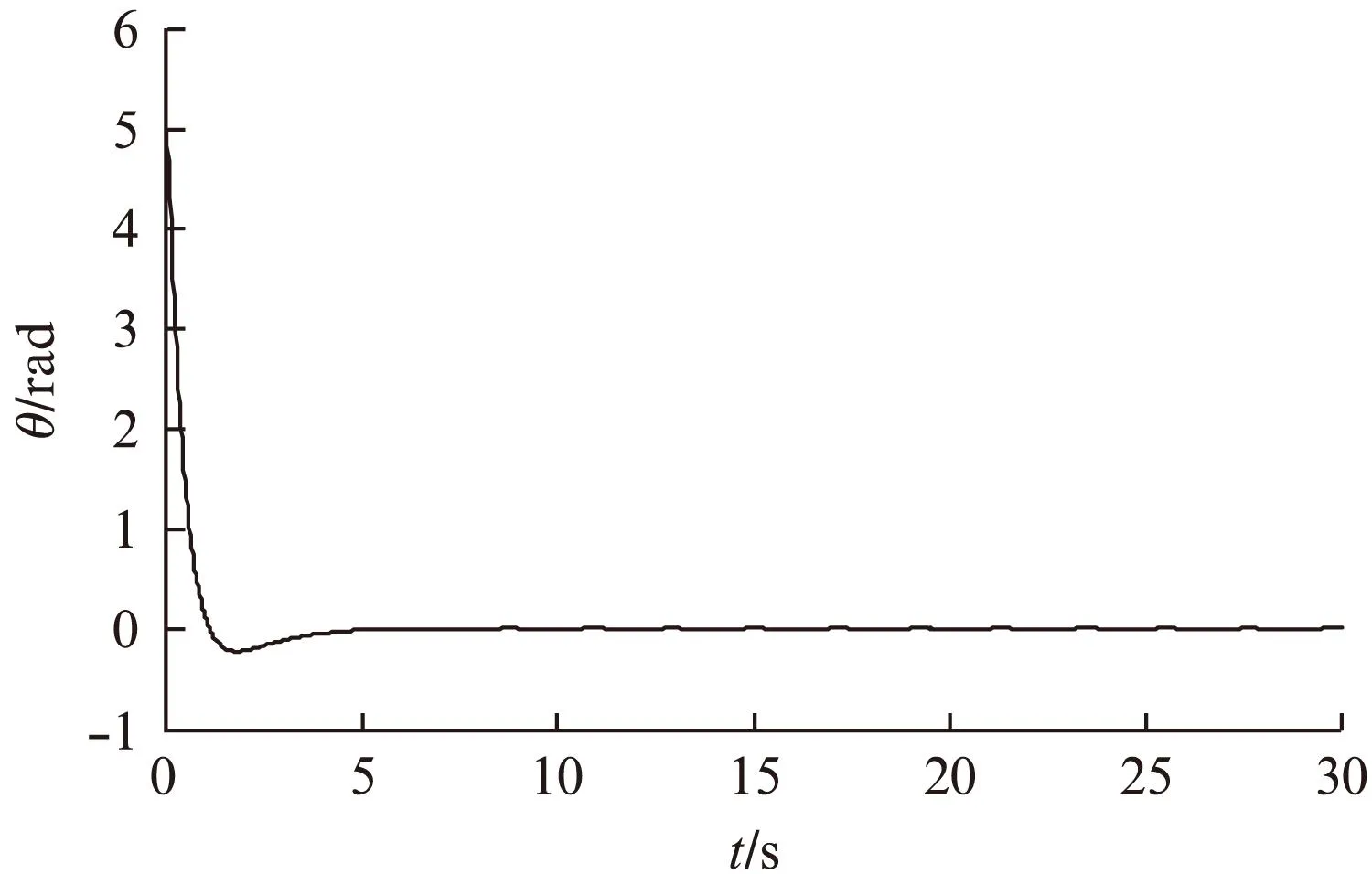
图2 倾角度跟踪响应曲线
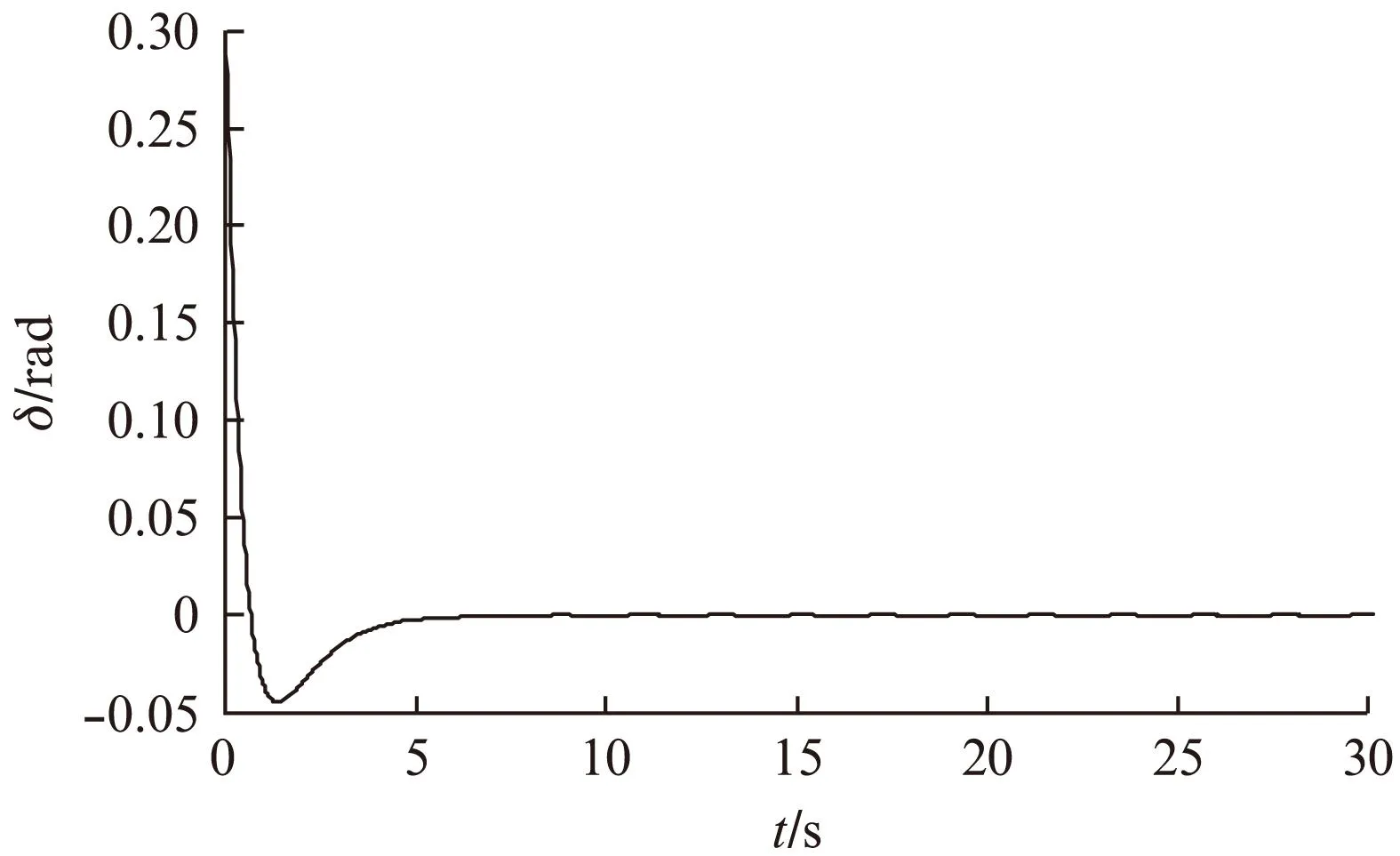
图3 转变角度跟踪响应曲线
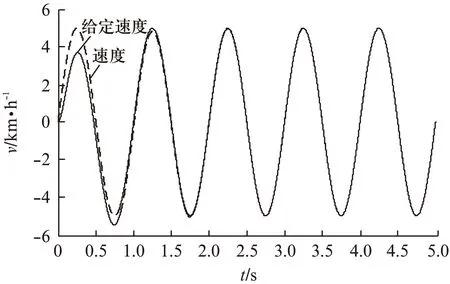
图4 线速度跟踪响应曲线
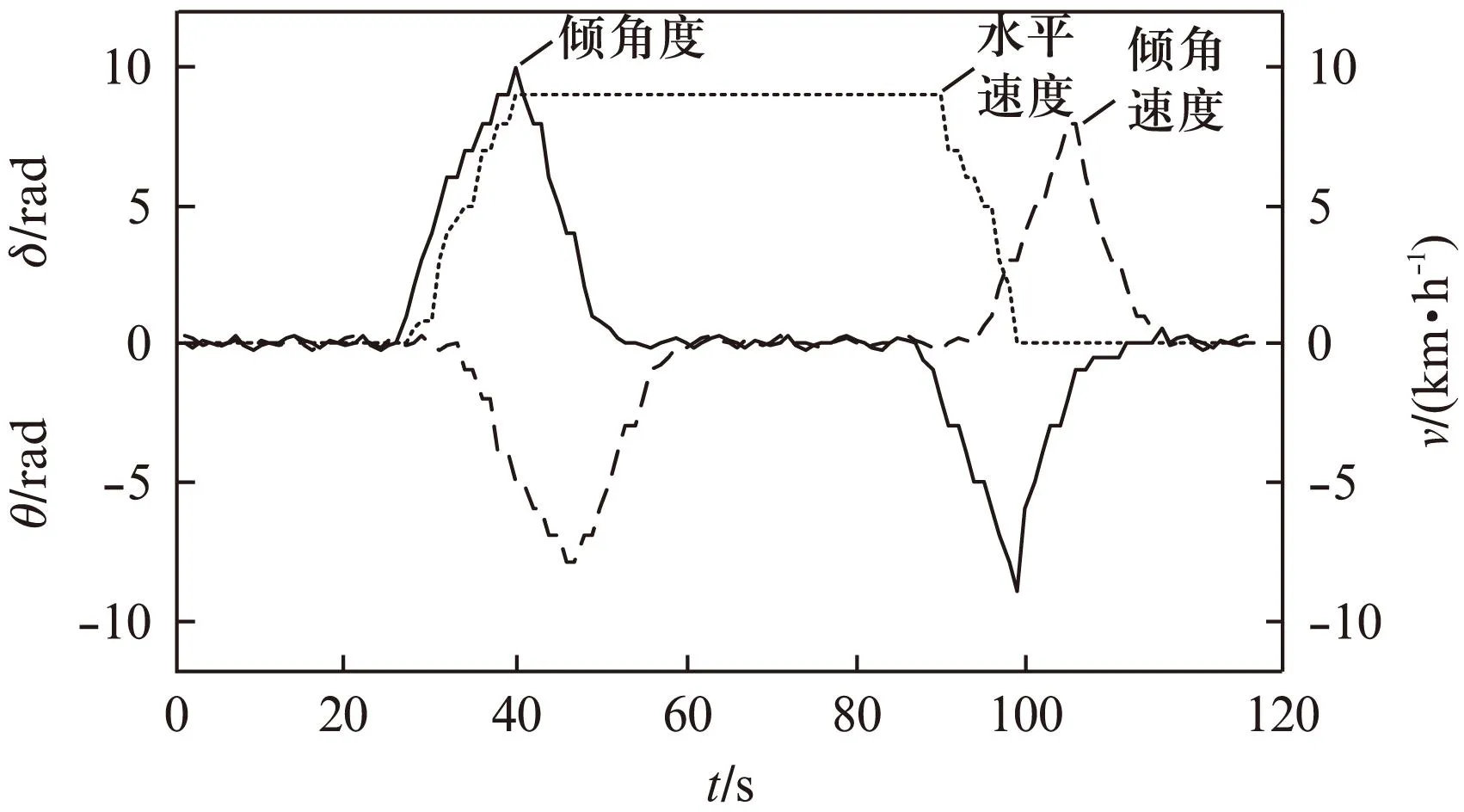
图5 系统平衡控制曲线
4结语
本文采用滑模控制及电机磁场定向控制思路,提供了两轮自平衡车的控制方法。首先,通过理论分析建立了系统数学模型,并对系统进行解耦处理;同时针对水平线速度控制、车体平衡控制、转弯控制3个子系统分别设计了滑模控制器;在此基础上,利用电机磁场定向控制思路,实现对自平衡车两轮驱动电机的控制;最后基于Simulink平台进行仿真。平衡控制、转弯及水平线速度等控制仿真结果表明,文献所提出的控制方法具有良好的控制性能。
【参 考 文 献】
[1]LIN S C, TAI C C, HUANG S C. Development of self-balancing human transportation vehicle for the teaching of feedback control[J]. IEEE Transactions on Education, 2009,26(2):1-52.
[2]阮晓钢,赵建伟.基于PWM伺服控制及LQR的两轮自平衡移动机器人[J].控制工程,2009,16(3):363-366.
[3]LIN S C, TAI C C, HUANG S C. Adaptive robust self-balancing and steering of a two wheeled human transportation vehicle[J]. Intel Robot System,2011,27(2):103-123.
[4]李明爱,焦利芳,乔俊飞.自平衡两轮机器人的分层模糊控制[J].控制工程,2009,16(1):80-82.
[5]杨兴明,高银平,朱建,等.基于分层滑模方法的两轮载人自平衡车的运动控制[J].合肥工业大学学报(自然科学版),2013(12):1456-1460.
[6]XU J X, GUO Z Q, LEE T H. Design and implementation of a takagi-sugeno type fuzzy logic controller on a two-wheeled mobile robot[J].IEEE Transaction on Industrial Electronics,2013,60(12):5717-5728.
[7]杨兴明,段举,朱建,等.基于模糊调节的两轮自平衡车的终端滑模分解控制[J].合肥工业大学学报(自然科学版),2014(10):1187-1193.
[8]武俊峰,李月.滑模变结构方法在两轮自平衡机器人上的应用[J].哈尔滨理工大学学报,2013,18(2):95-100.
[9]武俊峰,孙雷.两轮自平衡机器人的控制方法研究[J].哈尔滨理工大学学报,2014(6):22-26.
[10]ALAEINOVIN P, JATSKEVICH J. Filtering of hall-sensor signals for improved operation of brushless DC motors[J]. IEEE Transactions on Energy Conversion, 2012,27(2):547-549.
[11]郭超伟,高艳霞,张曲遥,等.基于滑模观测器的交流伺服电机无传感器控制[J].电机与控制应用,2015(4):1-5.
[12]HUANG J, GUAN Z, MATSUNO T, et al. Sliding mode velocity control of mobile-wheeled inverted-pendulum systems[J]. IEEE Transactions on Robotics,2010,26(4):750-758.
[13]杨代利,张宏立.基于全鲁棒滑模控制的永磁同步电机伺服系统矢量控制[J].电机与控制应用,2014(2):19-22.
Control of Two Wheeled Self-Balancing Vehicle Based on Sliding Mode Control*
CAIZhiduan,YUQinghui,ZHANGWenli,ZHANGYinxin,XUNQian
(School of engineering, Hu Zhou University, Huzhou 313000, China )
Abstract:In order to solve the balance control problem of two wheeled self-balancing vehicle and the influence of the mathematical model parameters on the control performance. The control method base on sliding mode and field-oriented control (FOC) of the motor was proposed. Firstly,the dynamic model of the two wheeled self-balancing vehicle and motor were established. The balance control system was decomposed into three subsystems. Secondly, a control scheme for the two wheeled self-balancing vehicle was established. The sliding mode control algorithm was used in the FOC of the motor. Lastly, the effect of the control method was analyzed by experiments. The simulation results show that the control method was effective.
Key words:sliding mode control; two wheeled self-balancing vehicle; motor
*基金项目:国家级大学生创新创业训练计划项目(201510347009);湖州市公益性技术应用研究计划项目(2015GZ05)
作者简介:蔡志端(1978—),男,博士研究生,讲师,研究方向为永磁同步电机控制技术、功率变换器故障诊断与容错控制。 余庆辉(1995—),男,本科,主要研究方向为电气工程及其自动化。
中图分类号:TM 301.2
文献标志码:A
文章编号:1673-6540(2016)05- 0028- 05
收稿日期:2015-12-04
荀倩(1990—),女,硕士研究生,讲师,研究方向为参数辨识与电机控制。
