基于全向小波和Hausdorff距离的边缘检测

张　涛，张　欣，杨卓东，杨臣君

(贵州大学 大数据与信息工程学院，贵州 贵阳 550025)

基于全向小波和Hausdorff距离的边缘检测

张涛，张欣，杨卓东，杨臣君

(贵州大学 大数据与信息工程学院，贵州 贵阳 550025)

摘要:针对传统小波变换对含噪图像边缘检测的不足，结合全向小波和Hausdorff距离的知识，提出了一种改进的边缘检测算法。首先，对图像做全向小波变换，同时做改进的灰度图形态学处理；然后在一定的窗口下求处理后图像间的Hausdorff距离，并将其大小作为图像边缘检测的像素值。最后将该算法与Sobel算法、Canny算法做比较，实验结果表明该方法提取的边缘清晰度优于其他方法，且可以很好地抑制噪声。

关键词:边缘检测；全向小波；Hausdorff距离；形态学处理

边缘是图像的基本特征之一，它在计算机视觉、模式识别以及图像分割中有着广泛的应用，在复杂环境下获取清晰的边缘是数字图像处理研究的一个重要方面，寻找能够适应各个方向且完全抑制噪声的边缘检测算法是当前的一个难题[1]。

传统的边缘检测算法有Sobel算子、Roberts和Canny算子等，但它们在边缘检测时难以满足抗噪的要求[2]。由于小波变换具有良好的时频特性，使其在图像处理中得到了很好的应用[3]，传统小波变换在进行边缘检测时对方向特征不敏感，许多学者提出了很多改进算法。Hao[4]等人通过改变小波尺度提取了图像边缘；Zhang[5]等人将偏微分方程融合到小波边缘检测中，在高频部分应用耦合卡通—纹理分解法实现了边缘检测；Lu[6]等人基于局部熵值和小波变换的知识，提出了自适应的尺度选择方法获取了图像的边缘；Li[7]提出了一种自适应阈值设定的小波边缘检测，能够自适应地对图像进行边缘检测；Qiao[8]等人将形态学运用到小波模极大值中进行边缘检测，获得了较好的效果；Li[9]等人提出了全向小波的概念，在获取图像的边缘时取得了很好的效果，但其抗噪性能有待改善。

本文结合全向小波、Hausdorff距离以及形态学的知识，提出了一种新的含噪图像边缘检测算法，达到了边缘提取与噪声抑制同时实现的目的，实验结果进一步证明了该算法的有效性与正确性。

1基本原理分析

1.1全向小波在边缘检测中的应用

边缘往往是信号中变化率最大的地方，因此可以用适度平滑的函数对图像进行滤波，然后再对其求导即可检测出边缘[10]。θ(x，y)设是一适度平滑的二维函数，满足如下条件

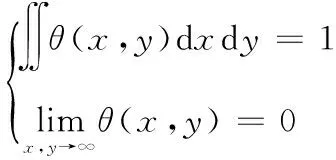
(1)

由此可以定义两个小波变换

(2)

在尺度为a时，记

(3)

可得到输入函数f(x,y)在水平方向的卷积小波变换

(4)

式中：*为卷积符号，则垂直方向的小波变换为

(5)

因此

(6)

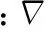
(7)

(8)

在尺度为α、小波方向为β时，李等人提出的全向小波变换为

[cos(α)cos(β)+sin(α)sin(β)]=

Mαf(x,y)cos(α-β)

(9)

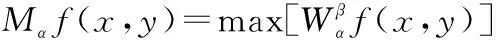
(10)

式(10)表明全向小波变换模值最大值的与数平滑后的梯度模值成正比。从而，在进行边缘检测时可用全向小波的值代替梯度模值。

1.2Hausdorff距离

Hausdorff距离度量的是从对象模型和测试图像中提取的两个边缘点集之间的距离值，其最初的定义为

HD(B,A)=max(d_hB,A),d_h(A,B)

(11)

A={a1,a2,…,an}，B=(b1,b2,…,bn)

(12)

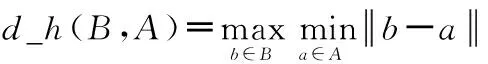
(13)

式中：A，B为边缘像素集；a,b为图像像素；‖·‖为像素间的欧氏距离。通常d_h(B,A)和d_h(A,B)是不一样的，Hausdorff距离表征了A与B最不匹配的最大距离，衡量了两个集合的不匹配程度。由于最初的Hausdorff距离对外部点比较敏感，施[11]等人提出了一种改进的Hasudorff距离表达式

(14)

式中：Nb是B中所有元素的个数。

1.3形态学在灰度图像中的应用

形态学处理是图像处理的另一种方式，令f(x，y)为输入图像，b(x，y)为结构元素；Df(x，y)与Db(x，y)是其定义域，则灰度图像形态学的膨胀操作、腐蚀操作、开操作与闭操作如下[12]

(15)

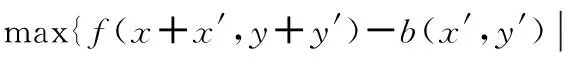
(16)

(f∘b)(x,y)=(f(x,y)⊗b(x,y))⊕b(x,y)

(17)

(f·b)(x,y)=(f(x,y)⊕b(x,y))⊗b(x,y)

(18)

2本文算法

1)选取式(19)作为二维平滑函数构造全向小波

(19)

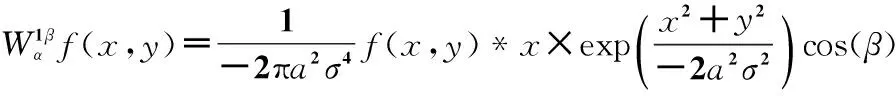
(20)

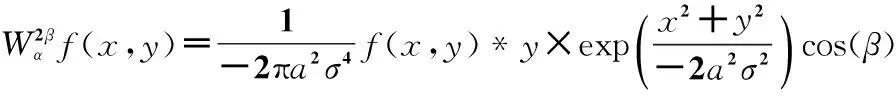
(21)

取平滑窗口的大小为3×3，σ2=1，尺度a=22，则

(22)

(23)

式中：β∈(0,2π)，取式(22)、(23)的最大值作为变换的结果，并赋值给集合A。

2) 传统的形态学边缘检测在抗噪声方面较差，本文提出了一种新的检测方法，其操作方法为

h(x,y)=(f(x,y)∘b2(x,y))⊕b1(x,y)-

(f(x,y)·b2(x,y))⊗b1(x,y)

(24)

式中：b1为5×5全“1”的结构元素，b2为3×3全“1”的结构元素。用此式对输入图像进行处理，将得到的检测结果作为集合B。

3) 为了将Hausdorff距离应用到边缘检测中，本文提出如下改进

HD(B,A)=min(d_h(B,A),d_h(A,B))

(25)

式中：d_h(B,A)如式(14)所示。这样Hausdorff距离就表征为A与B匹配的最小距离值，因此它反映了两集合之间的相似性，由此我们可以寻找出最优的边缘像素，用式(25)对集合A和B求Hausdorff距离，将其作为边缘检测的结果。

3实验结果

为了验证本文算法，使用MATLAB7.1进行实验，如图1所示，图1a的3个图从左至右依次为不含噪声的Lena图像、叠加方差为0.05的高斯白噪声图像、叠加方差为0.1的高斯白噪声图像。图1b表明Sobel算法有漏检的情况，如最左边的垂直竖线未完全检测出来，当加入噪声时，只检测出图像的大致轮廓，随着噪声方差的增加，其检测效果越来越差；图1c表明Canny 算法对细节的检测很精确，但其抗噪性能很差，当加入噪声后，Canny算法未能检测出图像的边缘；图1d表明在无噪声的情况下，本文算法在提取细节时介于Sobel算法和Canny算法之间，但当提取图像的轮廓时，其效果优于Sobel算法和Canny算法，且具有一定的抗噪性能。

a　原图

b　Sobel

c　Canny

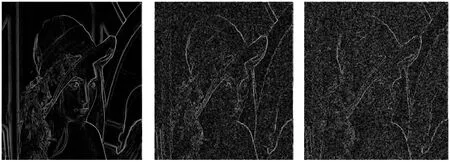
d　本文算法图1　不同边缘检测算法对比

为了从主观方面对本文算法进行评价，采用赵[13]等人的方法，对边缘检测的图像做信噪比的比较，其值越大，表示算法的抗噪性能越好，计算如式(26)所示

(26)

表1不同边缘检测算法的信噪比

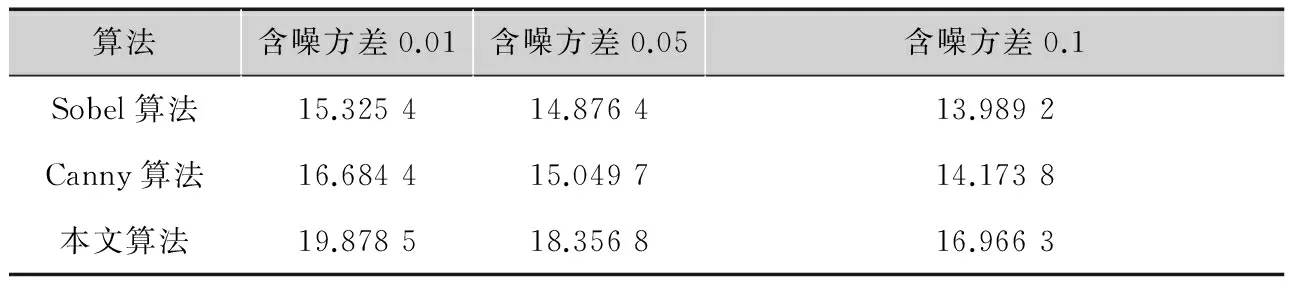
算法含噪方差0.01含噪方差0.05含噪方差0.1Sobel算法15.325414.876413.9892Canny算法16.684415.049714.1738本文算法19.878518.356816.9663

4结论

本文针对含噪图像在边缘检测中现存的问题，提出了一种基于全向小波和Hausdorff距离的边缘检测算法，全向小波变换可以检测各个方向的细节，灰度形态学可以检测图像大致的轮廓，所以结合两者的优点可以很好的检测边缘，为了使检测算法具有较好的抗噪性能，用Hausdorff检测两者的距离作为边缘检测的结果。实验结果表明本文算法在提取边缘的时候可以很好的抑制噪声，且具有较好的视觉效果。

参考文献：

[1]张闯，王婷婷，孙冬娇，等.基于欧氏距离图的图像边缘检测[J].中国图象图形学报，2013，18(2)：176-183.

[2]王拯洲，王伟，王维，等.基于多尺度自适应梯度的图像边缘检测方法[J].计算机工程与设计，2014，35(7)：2442-2446.

[3]兰旭光，郑南宁，吴勇，等.JPEG2000二维离散小波变换高效并行VLSI结构设计[J].西安交通大学学报， 2004， 38(2) ：149-153.

[4]郝燕玲，周文君，马海峰. 一种新的基于小波变换的图像边缘检测算法[J].传感器与微系统， 2008，27(3)：104-106.

[5]张力娜，李小林. 基于小波变换与偏微分方程的图像分解及边缘检测[J].计算机应用， 2013，33(8)： 2334-2336.

[6]卢萌，赵合计. 一种改进的小波自适应边缘检测算法[J].计算机应用研究，2011，28(1)：385-387.

[7]李红. 一种改进的基于小波变换的图像边缘提取方法[J].微电子学与计算机，2014， 31(9)：170-172.

[8]乔闹生，邹北骥，邓磊，等. 一种基于图像融合的含噪图像边缘检测方法[J].光电子·激光，2012，23(11)：2215-2220.

[9]李哲涛，李仁发，谢井雄. 基于全向小波的图像边缘检测算法[J].电子学报， 2012，40(12)：2451-2455.

[10]LIN S Y，SU G C，CHEN D，et al.Edgedetection based on wavelet transform and morphology [J].Chinese journal of scientific instrument， 2004， 25(4)：685-687.

[11]施光莹，马龙. 纹理豪斯多夫距离在人脸识别算法中的应用[J].计算机应用与软件，2014，31(10)：186-188.

[12]GONZALEZ R C， WOODS R E， EDIINS S L.Digital image processing using MATLAB [M].Beijing：Publishing House of Electronics Industry，2013.

[13]赵晓丽， 孔勇. 基于高斯小波的多尺度积图像边缘检测算法[J]. 数据采集与处理，2012，27(4)：490-494.

张涛(1990— )，硕士生，主要研究方向为数字图像处理；

张欣(1976— )，博士，副教授，主要研究方向为下一代无线通信技术及应用，为本文通讯作者；

杨卓东(1994— )，硕士生，主要研究方向为数字图像处理；

杨臣君(1991— )，硕士研究生，主要研究方向为无线通信技术。

责任编辑：时雯

Edge detection based on omni-directional wavelet and Hausdorff distance

ZHANG Tao，ZHANG Xin，YANG Zhuodong，YANG Chenjun

(SchoolofBigDataandInformationEngineering，GuizhouUniversity，Guiyang550025，China)

Abstract:In order to overcome the weakness of the traditional wavelet transform at the edge detection of noisy image， an improved edge detection algorithm based on the omni-directional wavelet and Hausdorff distance is proposed. Firstly， the Omni-directional wavelet transform detects the edge of the image， at the same time the method of improved gray morphology also detects the edge. Then， the Hausdorff distance can be calculated between two processed images under a certain window， and the value of distance is regarded as the pixel value of image edge detection. Finally， experimental comparison of the algorithm with Sobel algorithm and Canny algorithm. And the results prove that this method is better than others in image edge definition. Furth more the noise can be restrained well.

Key words:edge detection； omni-directional wavelet； Hausdorff distance； morphology processing

收稿日期;2015-08-04 2015-06-25

中图分类号:TP391.9

文献标志码:A

DOI：10.16280/j.videoe.2016.02.009

基金项目：国家自然科学基金项目(11204046);贵州省科技厅工业攻关项目(黔科合GY字[2010]3056)

作者简介：

文献引用格式：张涛，张欣，杨卓东，等.基于全向小波和Hausdorff距离的边缘检测[J].电视技术,2016，40(2)：50-53.

ZHANG T，ZHANG X，YANG Z D，et al.Edge detection based on Omni-directional wavelet and Hausdorff distance[J].Video engineering,2016,40(2)：50-53.