一种基于新型小波阈值去噪预处理的EEMD谐波检测方法

孙曙光，庞 毅，王景芹，张 超，杜太行，于 晗

(1.河北工业大学控制科学与工程学院，天津 300130；2.河北工业大学电气工程学院，天津 300130；3.陕西科技大学电气与信息工程学院，陕西 西安 710021)

一种基于新型小波阈值去噪预处理的EEMD谐波检测方法

孙曙光1，庞 毅1，王景芹2，张 超3，杜太行1，于 晗1

(1.河北工业大学控制科学与工程学院，天津 300130；2.河北工业大学电气工程学院，天津 300130；3.陕西科技大学电气与信息工程学院，陕西 西安 710021)

为了提升经验模态分解(EMD)用于谐波检测的效果，用集合经验模态分解(EEMD)消除了 EMD 谐波检测的模态混叠问题。通过研究发现采样信号中的噪声会对 EEMD 的分解产生较大影响，提出了一种基于新型小波阈值去噪预处理的EEMD 谐波检测方法。该方法首先采用变换小波系数精确选取小波阈值，然后采取软硬阈值相结合的方式，以消除随机噪声，再将去噪后的信号进行EEMD分解。经仿真分析，所提方法可以有效地消除随机噪声对谐波检测的影响，提高了 EEMD 谐波检测的精度与适用性。同时与原有 EEMD 算法相比，所提方法在分解速率上平均提高了大约 3.8 倍，有效分量与原始信号的相关度平均提升了 22.5%。

谐波检测；模态混叠；集合经验模态分解；小波系数；阈值

0 引言

随着非线性电力设备的广泛应用，电力系统中谐波问题越来越严重，尤其近年来分布式电源被广泛应用，日益成为人们研究的热点[1]，但由于微电源的接入给电力系统的电能质量产生影响，特别是谐波污染问题尤为严重；此外，正如火如荼发展的电动汽车，其车载充电器就是非线性负荷，根据工信部消息，2014 年 12 月我国纯电动乘用车生产 1.2万量，同比增长近 14倍，一旦大规模车载充电器接入电网会给配电系统带来很大的谐波[2-3]。

为了消除谐波，提高电能质量，必须准确地检测出各次谐波分量。近年来，经验模态分解(Empirical Mode Decomposition，EMD)技术在电力系统中应用逐步增多，该方法能够自适应地将采集到的电力信号分解成不同尺度的模态函数，但由于实际应用中谐波分量分布不均匀且频率没有连续性，导致 EMD分离出的固有模态函数(Intrinsic Mode Function，IMF)存在模态混叠现象。针对这一问题，集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)方法以 EMD 为核心，继承其优点，通过叠加白噪声的方法，有效地抑制了模态混叠[4-8]。

由于电力系统结构复杂且干扰多，实际采集的信号中常受噪声污染，对于谐波检测不仅需要最大限度地滤除噪声，而且要尽可能地保留谐波和基波信号。由于存在噪声的干扰会影响到 EEMD谐波分解的质量[9]，针对噪声问题，本文提出一种新的小波阈值去噪方法，在小波阈值的选取上，由于小波阈值去噪中的难点在于区分信号和噪声，对于一些低信噪比的信号中与噪声相近的区域较多，容易被当成噪声滤除掉，所以本文采用小波系数变换的方法，将信号中易混淆的中间部分进行差别放大，两端不易混淆的部分值域相应缩小[10-11]，如此易于去噪时对噪声的识别。在阈值函数的选取上，针对传统小波阈值处理中硬阈值的不连续性和软阈值存在恒定偏差的特性，采用软硬阈值相结合的方式，从而克服了硬阈值和软阈值的弊病[12-13]。综合以上，本文提出基于小波系数变换的软硬阈值相结合的去噪预处理方法，继而利用 EEMD进行谐波分解，提高了谐波检测的精度和运行效率。通过 Matlab 仿真，以信噪比、均方误差、相关度和分解速率作为相应的评价标准进行去噪以及谐波检测的效果分析，验证此方法在谐波检测中的优势。

1 基于 EEMD 的谐波检测方法

1.1 EMD分解原理

EMD 用于处理非平稳和非线性信号，该方法在时间和频域平面上将原始信号 ()Xt 分解为多个 IMF分量信号iC,1 i n£ £

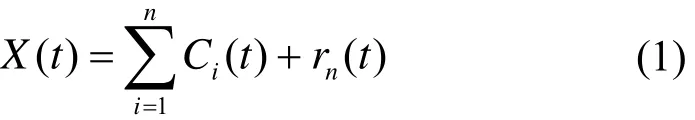
式中，nr 是剩余分量。所谓的 IMF 要满足两个条件：1) 整个 IMF 信号中过零点与极值点个数相等或至多相差一个；2) 由局部极大值点确定的上包络线与局部极小值点确定的下包络线的均值为零。每个IMF分量是通过筛选得来的。EMD分解的详细步骤可以参考文献[4-6]。

1.2 EEMD方法的原理

模态混叠是 EMD 算法的一个缺陷。模态混叠主要包括不同尺度成分存在于一个 IMF 分量中或者相似尺度成分出现在不同的 IMF 中。针对这一问题本文采用 EEMD技术，该方法能消除大部分的模态混叠问题，并保持模态信号的固有特性[14]。

EEMD 是以 EMD 算法为核心进行的改进，所以 EEMD 和EMD的主要算法结构大体相同。具体步骤为

1) 将高斯白噪声 ()tw 加入目标信号 )(tx 得到一个总体信号；

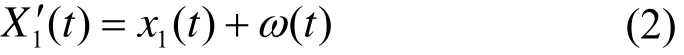
2) 将总体信号进行 EMD 分解，得到各阶 IMF分量；

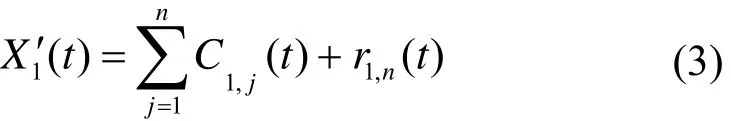
3) 重复步骤 1)-2)，但是每次加入的高斯白噪声 wi( t)是不同的；

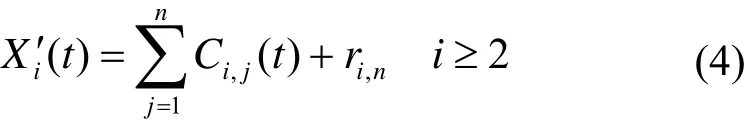
4) 利用高斯白噪声频谱的零均值原理，消除高斯白噪声作为时域分布参考结构带来的影响，分解相应的 IMF 分量的整体平均值就是最终的结果，Cn(t)可表示为

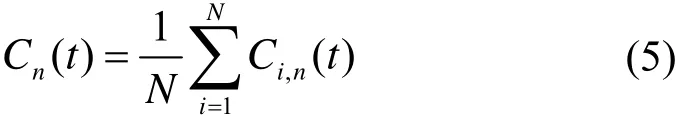
EEMD 中高斯白噪声的加入服从式(6)。

式中：e为高斯白噪声的幅值；N为总体个数；ne表示原始信号与各阶的 IMF 相加后之间的误差。为了保证谐波检测算法的快速性，一般选取e为 0.01，N=200。

1.3 谐波电流检测实验分析

本文参考日常生活中电网实际负载电流的情况，引入一种典型的负载电流模型，表达式为

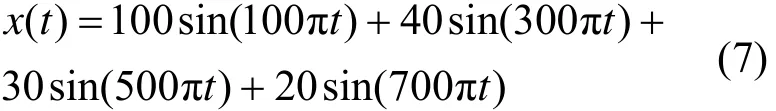
此信号中含有四种成分，式中第 1项代表基波，频率 50 Hz，幅值为 100 A，其余 3 项分别为 3、5、7 次谐波，幅值大小分别为 40 A、30 A、20 A，采样频率设置为 12 800 Hz。图1 为该模型的波形图，电流正弦度差，发生畸变。

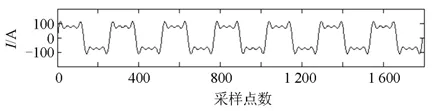
图1 谐波源电流Fig. 1 Harmonic source current

通过给定的谐波电流模型，下面来验证EEMD处理模态混叠问题的效果。图2为 EMD 对给定谐波信号的分离结果，由 EMD 算法可知，分离的 IMF应该依次为7次、5次、3次、基波和剩余分量。除了剩余分量外，都应该是正弦波。但是通过图2可以看出，前两条 IMF 分量并不是单一分量，均出现模态混叠问题。图3为 EEMD 分离的结果，并没有出现模态混叠现象，而且均保留了每条 IMF 的固有特性。忽略端点效应的影响，图2和图3相比较，EEMD 能够很好地消除模态混叠的问题。

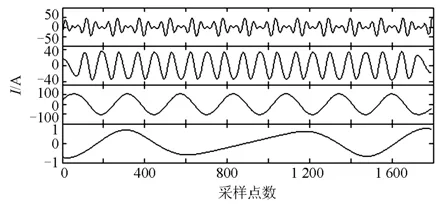
图2 EMD 谐波检测结果Fig. 2 Detection results of EMD

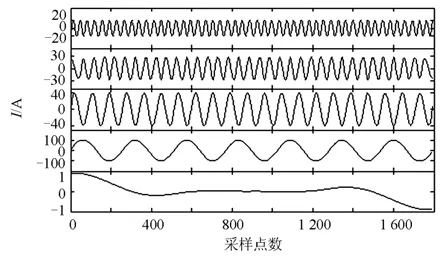
图3 EEMD 谐波检测结果Fig. 3 Detection results of EEMD

1.4 噪声对谐波检测的影响

为了分析噪声对 EEMD分解的影响，本文对给定的电流谐波信号加入高斯白噪声，加噪后信噪比为 24 dB。图4 为叠加噪声的电流信号，上曲线表示噪声信号，下曲线表示叠加噪声后的电流信号。图5为 EEMD 对含噪声的电流信号分解的结果。从图5 可以看出，前两项 IMF 为高频噪声分量，后面4项为谐波和基波的分量，但是由于噪声的影响，EEMD并不能够很好地将谐波和基波信号准确地分离出来，各模态分量都发生了很大的畸变。所以噪声的存在对于 EEMD 谐波检测结果的准确性有着直接的影响。

因此，更好地滤除噪声直接关系到EEMD 谐波检测的质量。通过分析与研究，本文提出了一种新的小波阈值去噪方法进行信号预处理。

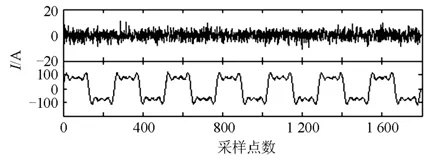
图4 加入噪声的电流信号Fig. 4 Current harmonic signal with noise

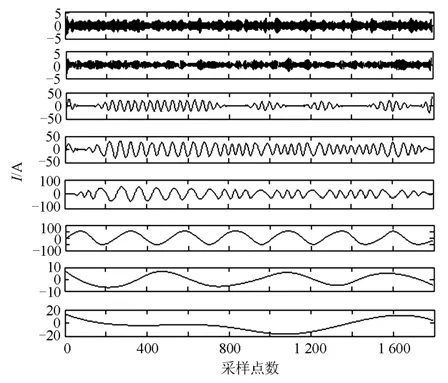
图5 EEMD 对含噪声的电流信号分解结果Fig. 5 EEMD decomposing results for harmonic signal with noise

2 新型的小波阈值去噪方法

由 Donoho 和 Johnstone提出的小波阈值去噪是一种有效的去噪方法。在电网谐波检测中，有用信号一般为低频信号，噪声信号一般为高频信号。根据这一特点，小波阈值去噪的步骤主要分三步[15-17]：

1) 选择合适的小波基，确定分解层数，然后对信号进行小波分解；

2) 对高频部分的小波系数进行阈值处理；

3) 对处理后的小波系数进行重构，得到去噪后的信号。

以上步骤中，选取合适的阈值和阈值函数直接关系到去噪效果的好坏。

2.1 改进的小波阈值函数

对于阈值的选取，Donoho 和 Johnstone 给出的固定阈值为

式中：N为小波分解后各层小波系数的长度；s为估计噪声的方差，s=MAD/0.6745，MAD 是第一层小波分离后高频小波系数的均值。在阈值函数算法中，硬阈值和软阈值是最常用的两种阈值函数。

软阈值函数为

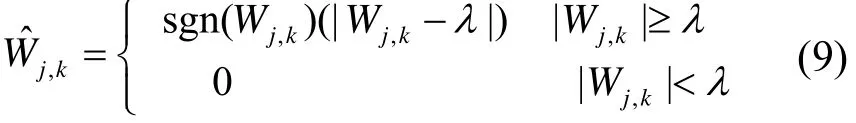
硬阈值函数为

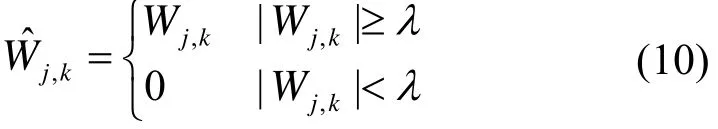
式中：,jkW 为各层的小波系数；l为小波阈值。根据式(9)和式(10)可知，这两种阈值算法均存在一定的缺陷。在硬阈值算法上，阈值l处不连续，缺少像原始信号一样的光滑性；软阈值相对来说，虽然整体的连续性较好，但是阈值处理前后的小波系数存在恒定的偏差。针对两种阈值函数的不足,本文采用一种改进的阈值函数，如式(11)。

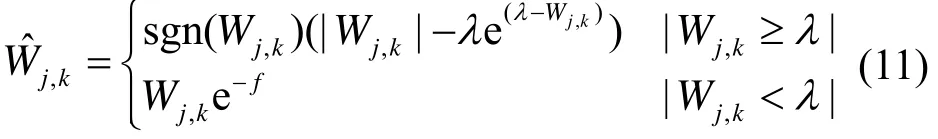
式中，f为信号的频率。对改进的阈值函数在阈值l处求取极限可知：

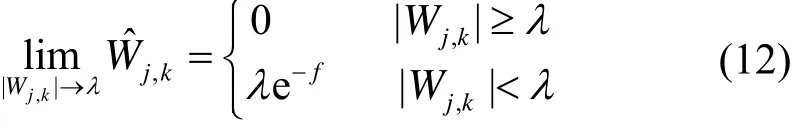
2.2 基于变换小波系数的软硬阈值相结合去噪方法

在谐波检测中，小波系数较高的一般属于谐波和基波电流的分量，较低的一般属于噪声分量。较高系数和较低系数部分都不会产生误判断。但在低信噪比条件下，信号与噪声的中间系数部分较多，容易将信号混淆为噪声被滤除掉，因此，选择合适的阈值成为了一个难点。因此本文采用变换小波系数的方式对中间易混淆部分进行差别放大。基于此，变换函数需满足在小波系数范围内单调连续且导数从较小逐渐增大，如此使小波系数中间区域的系数进行放大便于识别，再通过式(8)精确计算小波阈值。式(13)满足以上要求，作为变换函数，进行小波系数变换，有利于阈值的选取和筛选。然后再将筛选后的小波系数根据式(14)进行反变换，还原原始系数。参照文献[10]，本文选用的变换函数和反变换函数为

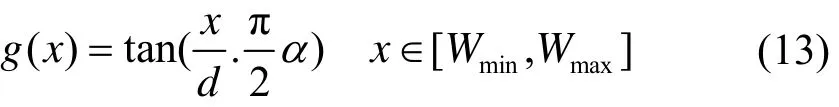
基于此本文提出了基于变换小波系数的软硬阈值结合的去噪方法。步骤图如图6所示。

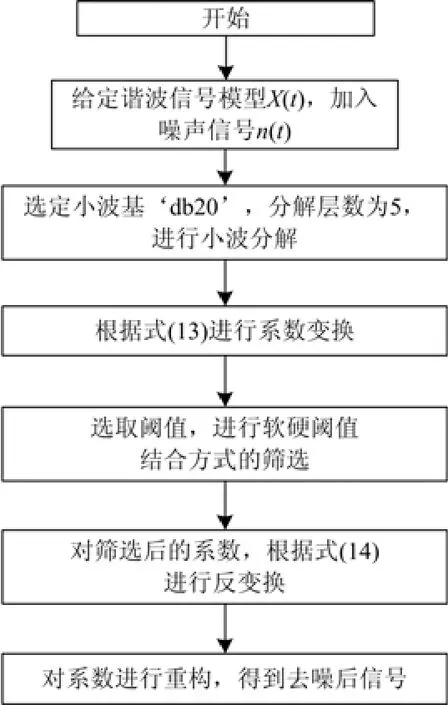
图6 本文去噪方法步骤Fig. 6 Denoising steps of this paper

新的小波阈值去噪方法通过变换小波系数增强了对含噪信号中某些细微信号的识别性，解决了阈值选取上的难点；通过软硬阈值相结合方式，解决了硬阈值函数和软阈值函数存在的弊病。如此，使去噪效果更好，同时尽可能保留有用信号的原始特性。

2.3 实验分析

为分析新的小波阈值去噪方法的效果，以信噪比(SNR)和均方根误差(RMSE)作为评判标准[18-20]。根据式(15)和式(16)知道，SNR 越大，RMSE 越小说明去噪效果越好，以此作为评判准则。

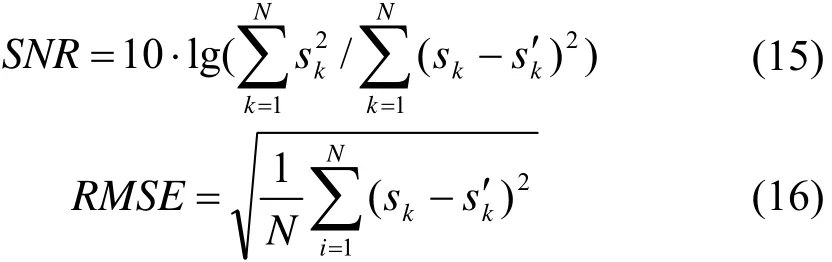
式中：ks 表示不含噪声的纯净原始信号；ks¢表示去噪后的信号。本文小波去噪选取的小波基为‘db20’，分解层数为5层。下面以图4的含噪声信号进行去噪处理，图7(a)~图7(d)依次为硬阈值方法、软阈值方法、软硬阈值相结合方法以及新的小波阈值去噪方法的去噪效果。图中第一条曲线为该方法的去噪效果，第二条曲线为去噪后信号与原始信号的差值。忽略端点问题，根据图形可以判断出本文所提的新的去噪方法效果最好。

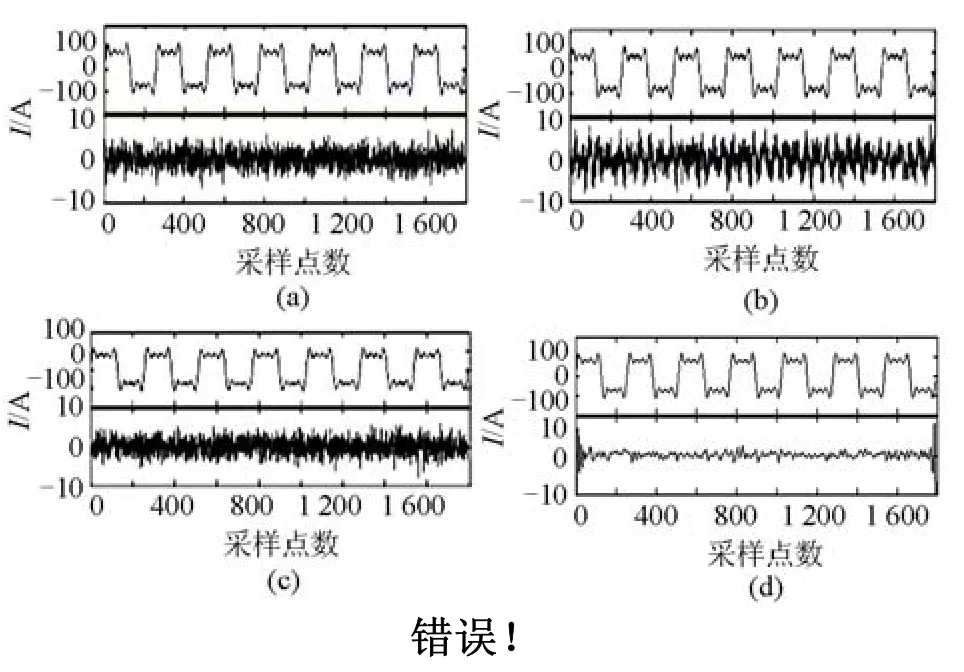
图7 不同方法的去噪效果Fig. 7 Denoising effect for different methods

参照评价标准，根据表1实验结果可以得出，软硬阈值相结合的方法优于单一的软阈值或者硬阈值。此外，从表1中可以明显地看出，本文新的去噪方法效果是最好的。

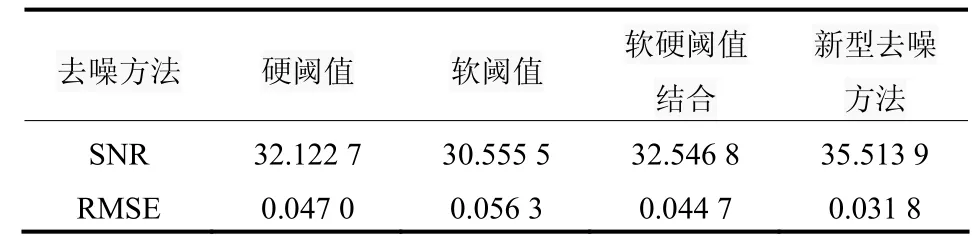
表1 不同方法去噪效果的比较Table 1 Comparison of denoising effect for different methods

通过以上实验数据分析，本文所提出新型小波阈值去噪方法针对软阈值和硬阈值各自存在的问题以及阈值选取上的难点都给予了一定的改善，使得去噪效果大大提高。

3 基于新型小波阈值去噪预处理的 EEMD 谐波检测分析

对于谐波检测而言，传统的快速傅里叶变换(Fast Fourier Transform，FFT) 是一种常用的方法，但其在非同步采样情况下存在较大的误差，而且在检测过程中，很难实现同步采样，导致其在检测时存在频谱泄露和栅栏效应，虽然通过插值、加窗可抑制栅栏效应和频谱泄漏现象，但会引入虚假成分；且其对非平稳信号的处理存在限制，其忽略了频率的瞬时性，不能恰当地表达信号本质特性[8]。然而EEMD 利用信号的局部特征时间尺度，完全根据信号性质自适应进行分解，从原始信号中提取出若干阶固有模态函数，可以准确有效地把握原数据的特征信息[5]。

基于以上分析，本文提出了一种基于新型的小波阈值去噪预处理的 EEMD 方法。方法如图8。

图8 本文谐波检测方法步骤Fig. 8 The steps of harmonic detection in this paper

图9 为本文方法(如图8 所示)对图4 含噪声的谐波进行检测的结果，从上到下前3项依次为 7次、5次、3次谐波，第4项为基波，第5项为剩余分量。根据图9与图5可以清楚得出，该方法能够有效地消除噪声对 EEMD分解的影响，且很好地保留原有谐波的特性。图10 为各次分离后谐波分量与给定谐波分量的对比，根据上文式(7)的谐波函数模型，虚线为给定谐波模型的标准信号，实线为本文方法分离后的各个分量。由图可知，分离后的各次分量和原有信号的基波与谐波分量非常吻合，验证了本文方法对于谐波检测具有很高的精度。

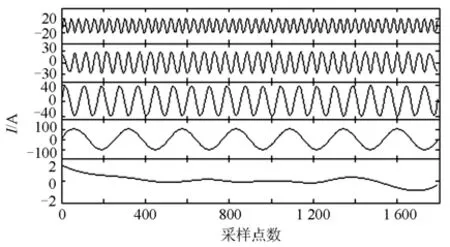
图9 本文方法对含噪声的电流信号的分解结果Fig. 9 Decomposing results for current signal with noise by new method

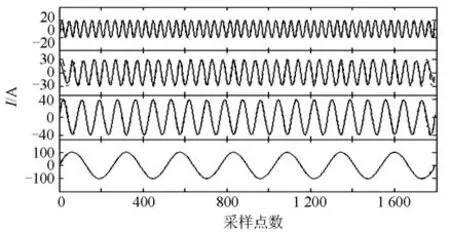
图10 各次谐波模态的对比效果Fig. 10 Contrast of every harmonic modal

此外，本文还通过常规EEMD 方法和本文方法(如图8 所示方法)对含噪声谐波信号的分解结果进行数据分析。通过 Matlab 中的 corrcoef函数求取有效分量与原始信号中相应分量的相关度进行对比[2]。根据给定谐波信号特点，分解后应有 4 条有用分量，根据由高频到低频的分解特性，表2 中 1-4序号分别表示7次、5次和3次谐波以及基波。从表2中可以看出本文方法明显优于EEMD的分解结果，得到的有效分量与原始信号的相关系数平均达到 0.985 9，相比较 EEMD 的分解结果，相关度平均提高了 22.5%。此外，还对两种方法的分解速率进行比较，表2中可以明显看出，在含有噪声的情况下，本文检测方法的分解速率相比较 EEMD 提高了 3.8 倍。

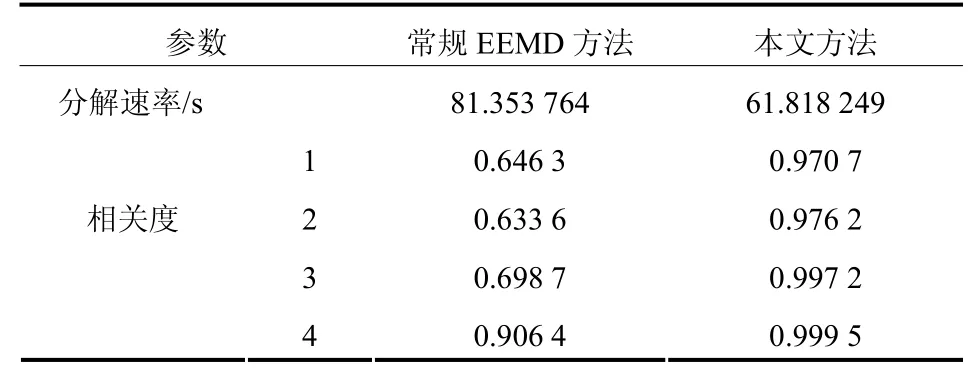
表2 不同方法分解效果对比Table 2 Comparison of decomposition effect for different methods

4 结论

本文根据谐波检测在应用中遇到的问题进行了研究与分析，提出了一种基于新型的小波阈值去噪预处理的 EEMD谐波检测方法。经实验分析表明该方法不仅能够消除 EMD 的模态混叠问题，同时该方法针对谐波信号的特点，采用变换小波系数精确计算阈值，加强了对易与噪声混淆的信号的识别性，同时采用软硬阈值相结合的方式，从而最终更好地提升了整体的去噪效果。因此本文方法不仅能够有效地去除随机噪声的影响，还能准确地保留谐波信号的固有特性，而且有着非常高的检测精度，同时还提升了分解速率和适用性。

此外，由于 EEMD 的检测算法需要不断地迭代运算，计算量较大，由于处理器速率的原因，在实际应用中可能达不到实时检测的要求，但是相信随着电子信息技术的发展，该算法应用范围会更加广泛。

[1]韩民晓, 刘迅. 分布式电源并网中电能质量相关规范探讨[J]. 电力设备, 2007, 8(1): 57-60. HAN Minxiao, LIU Xun. Power quality standard consideration for the connection of distributed generation to main grid[J]. Electrical Equipment, 2007, 8(1): 57-60.

[2]王成山, 武震, 李鹏. 微电网关键技术研究[J]. 电工技术学报, 2014, 29(2): 1-9. WANG Chengshan, WU Zhen, LI Peng. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 1-9.

[3]汪飞, 毛华龙, 许德志, 等. 多变电网条件下的对称序列 与 谐 波 检 测 [J]. 电 工 技 术 学 报 , 2014, 29(12): 158-165. WANG Fei, MAO Hualong, XU Dezhi, et al. Symmetrical sequence and harmonic detection in varied grid conditions[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 158-165.

[4]朱宁辉, 白晓民, 董伟杰. 基于 EEMD 的谐波检测方法[J]. 中国电机工程学报, 2013, 33(7): 92-98. ZHU Ninghui, BAI Xiaomin, DONG Weijie. Harmonic detection method based on EEMD[J]. Proceedings of the CSEE, 2013, 33(7): 92-98.

[5]于兴林, 李慧敏, 李天云. 基于 EEMD 和 TLS-ESPRIT的 谐 波 间 谐 波 检 测 方 法 [J]. 电 力 系 统 保 护 与 控 制 . 2014, 42(4): 67-72. YU Xinglin, LI Huimin, LI Tianyun. A harmonic and inter-harmonic detection method based on EEMD and TLS-ESPRIT[J]. Power System Protection and Control, 2014, 42(4): 67-72.

[6]周二磊, 张课, 董苏. 基于 EEMD 阈值去噪的电能质量 扰 动 检 测 研 究 [J]. 华 东 电 力 , 2013, 41(10): 2090-2094. ZHOU Erlei, ZHANG Ke, DONG Su. Power quality disturbance detection based on EEMD threshold denoising[J]. East China Electric Power, 2013, 41(10): 2090-2094.

[7]张佩, 赵书涛, 申路, 等. 基于改进 EEMD 的高压断路器振声联合故障诊断方法[J]. 电力系统保护与控制, 2014, 42(8): 77-81. ZHANG Pei, ZHAO Shutao, SHEN Lu, et al. Research on vibration and acoustic joint mechanical fault diagnosis method of high voltage circuit breaker based on improved EEMD[J]. Power System Protection and Control, 2014, 42(8): 77-81.

[8]李正明, 徐敏, 潘天红, 等. 基于小波变换和 HHT 的分布式并网系统谐波检测方法[J]. 电力系统保护与控制, 2014, 42(4): 34-39. LI Zhengming, XU Min, PAN Tianhong, et al. A harmonic detection method for distributed connected grid system by using wavelet transform and HHT[J]. Power System Protection and Control, 2014, 42(4): 34-39.

[9]樊刘娟, 冯秀芳, 朱晓军. 一种基于小波预处理的改进 总 体 经 验 模 态 分 解 方 法 [J]. 计 算 机 测 量 与 控 制 , 2013, 21(6): 1601-1604. FAN Liujuan, FENG Xiufang, ZHU Xiaojun. An improved ensemble empirical mode decomposition method based on wavelet pretreatment[J]. Computer Measurement & Control, 2013, 21(6): 1601-1604.

[10]王宏强, 尚春阳, 高瑞鹏, 等. 基于小波系数变换的小波 阈 值 去 噪 算 法 [J]. 振 动 与 冲 击 , 2011, 30(10): 165-168. WANG Hongqiang, SHANG Chunyang, GAO Ruipeng, et al. An improvement of wavelet shrinkage denoising via wavelet coefficient transformation[J]. Journal of Vibration and Shock, 2011, 30(10): 165-168.

[11]李化, 杨新春, 李剑, 等. 基于小波分解尺度系数能量最大原则的 GIS 局部放电超高频信号自适应小波去噪[J]. 电工技术学报, 2012, 27(5): 84-85. LI Hua, YANG Xinchun, LI Jian, et al. The maximum energy of wavelet decomposition approximation-related adaptive wavelet de-nosing for partial discharge UHF pulse GIS[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 84-85.

[12]苏立, 南海鹏, 余向阳, 等. 基于改进阈值函数的小波降噪分析在水电机组振动信号中的应用[J]. 水力发电学报, 2012, 31(3): 246-251. SU Li, NAN Haipeng, YU Xiangyang, et al. Application of wavelet denoising of improved threshold function to vibration signal analysis of hydroelectric units[J]. Journal of Hydroelectric Engineering, 2012, 31(3): 246-251.

[13]刘晓光, 胡静涛, 高雷, 等. 基于改进小波阈值的微机械陀螺去噪方法[J]. 中国惯性技术学报, 2014, 22(2): 233-236. LIU Xiaoguang, HU Jingtao, GAO Lei, et al. Micro mechanical gyro denoising method based on improved wavelet threshold[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 233-236.

[14]任 学 平 , 庞 震 , 辛 向 志 , 等 . 基 于 改 进 小 波 包 和EEMD 的轴承故障诊断[J]. 轴承, 2014(6): 41-44. REN Xueping, PANG Zhen, XIN Xiangzhi, et al. Fault diagnosis for bearings based on improved wavelet packet and EEMD[J]. Bearing, 2014(6): 41-44.

[15]杜修力, 何立志, 候伟. 经验模态分解(EMD)的小波阈值 除 噪 方 法 [J]. 北 京 工 业 大 学 学 报 , 2007, 33(3): 265-272. DU Xiuli, HE Lizhi, HOU Wei. A study of wavelet threshold denoising based on empirical mode decomposition (EMD)[J]. Journal of Beijing University of Technology, 2007, 33(3): 265-272.

[16]李洋, 景新幸, 杨海燕. 基于改进小波阈值和 EMD 的语音去噪方法[J]. 计算机工程与设计, 2014, 35(7): 2462-2466. LI Yang, JING Xinxing, YANG Haiyan. Speech de-noising method based on empirical mode decomposition and improved wavelet threshold[J]. Computer Engineering and Design, 2014, 35(7): 2462-2466.

[17]吴光文, 王昌明, 包建东, 等. 基于自适应阈值函数的小波阈值去噪方法[J]. 电子与信息学报, 2014, 36(6): 1340-1347. WU Guangwen, WANG Changming, BAO Jiandong, et al. A wavelet threshold de-noising algorithm based on adaptive threshold function[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1340-1347.

[18]钟建军, 宋健, 由长喜, 等. 基于信噪比评价的阈值优选小波去噪法[J]. 清华大学学报, 2014, 54(2): 259-263. ZHONG Jianjun, SONG Jian, YOU Changxi, et al. Wavelet de-noising method with threshold selection rules based on SNR evaluations[J]. Journal of Tsinghua University, 2014, 54(2): 259-263.

[19]MO Jialing, HE Qiang, HU Weiping. An adaptive threshold de-noising method based on EEMD[C]// Signal Processing, Communications and Computing (ICSPCC), 2014 IEEE International Conference on: IEEE, 2014: 209-214.

[20]张超, 马小平, 张义君, 等. 间谐波环境下并联有源滤波器系统设计[J]. 电工技术学报, 2015, 30(20): 118-125. ZHANG Chao, MA Xiaoping, ZHANG Yijun, et al. System design of shunt active power filter for interharmonics[J]. Transactions of China Electrotechnical Society, 2015, 30(20): 118-125.

(编辑 葛艳娜)

EEMD harmonic detection method based on the new wavelet threshold denoising pretreatment

SUN Shuguang1, PANG Yi1, WANG Jingqin2, ZHANG Chao3, DU Taihang1, YU Han1
(1. School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China; 2. School of Electrical Engineering, Hebei University of Technology, Tianjin 300130, China; 3. College of Electrical and Information Engineering, Shaanxi University of Science and Technology, Xi’an 710021, China)

In order to promote the effect of empirical mode decomposition (EMD) for the harmonic detection, this paper uses the ensemble empirical mode decomposition (EEMD) to eliminate the modal mixing of EMD harmonic detection. After studying, it is found that the noise in the sampling signal has great influence on the EEMD harmonic decomposition. This paper proposes an EEMD harmonic detection method based on a new wavelet threshold denoising pretreatment. This method adopts transforming wavelet coefficients to select threshold accurately, then uses the combination of hard and soft threshold and finally eliminates random noise. After simulation and analysis, this method can effectively eliminate the influence of random noise on harmonic detection and improve the accuracy and applicability of EEMD harmonic detection, and meanwhile, compared with the original EEMD algorithm, the decomposition rate increases about 3.8 times and the correlation between the effective components and the original signals increases by 22.5% .

harmonic detection; mode mixing; ensemble empirical mode decomposition; wavelet coefficients; threshold

TM77

1674-3415(2016)02-0042-07

2015-03-24；

2015-05-12

孙曙光(1979-),男，博士，副教授，主要从事谐波抑制以及无功补偿；E-mail: sunshuguang_2000@163.com

庞 毅(1990-),男，硕士研究生，主要从事谐波抑制以及无功补偿；

王景芹(1964-),女，博士，教授，研究方向为电器可靠性与电接触理论及应用。

天津市科技支撑重点项目(12ZCZDGX014000)；河北省高等学校科学技术研究重点项目(ZD2014051)；河北工业大学博士科研启动费资助项目