一种噪声未知的新型空间频谱分布协作感知算法

吴　名　 宋铁成　 沈连丰　 胡　静

(东南大学移动通信国家重点实验室, 南京 210096)

一种噪声未知的新型空间频谱分布协作感知算法

吴名 宋铁成 沈连丰 胡静

(东南大学移动通信国家重点实验室, 南京 210096)

摘要:为了获得占用频段、主用户发射功率、位置和本地噪声等全局信息,给出了一种主用户全局功率谱模型,提出了一种噪声未知的新型空间频谱分布协作感知算法.利用变分贝叶斯推断理论,估计出模型系数向量和本地噪声向量,以求得全局信息.仿真结果表明,所提算法在较高信噪比下具有较高的估计精度和收敛稳定性.该算法性能虽弱于噪声已知算法的性能,但相比基于非负最小二乘准则的算法具有更好的均方误差性能.

关键词:认知无线电;空间频谱分布;协作频谱感知;变分贝叶斯推断;稀疏性

目前,认知无线网络主要采用协作频谱感知技术，即利用从用户采样的分集特性来增强感知的性能，从而有效地复用空闲频谱,解决频谱利用效率低下这一现存困境[1-3].但是,鉴于主/从用户间距较大、从用户发射信号较小、存在建筑物阻挡等原因，从用户通信仅会在部分区域中对主用户通信产生有害干扰.此外,由于主/从用户存在移动性,主用户所受干扰的区域范围也随着时间不断变化.如何感知主用户占用频段、发射功率及其所处位置等空间频谱分布信息,成为实现认知网络动态全局频谱共享的首要问题.文献[4-5]指出，主/从用户位置的差异会导致不同的路径损耗，从而产生较大的动态频谱复用机会；文献[6]为体现由移动性引起的频谱接入机会，构建了相应的信道可用性模型；文献[7]构建了接近真实的移动性模型,并设计了相应的感知节点选择方法;文献[8]扩展出新的空时频谱感知模型,并定义了相应的性能评价指标;文献[9]利用新出现的变分贝叶斯推断技术,设计了一种噪声已知的新型空间频谱分布协作感知算法,得到主用户信号的占用频段、功率和所处位置等3种空间频谱分布信息.本文在文献[9]的基础上,进一步将本地噪声纳入全局功率谱模型进行统一建模,并设计了相应的空间频谱分布协作感知算法.

1系统建模

(1)

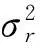
在仅考虑单个用户且无噪声的情况下,假设信道hsr(τ;t)和信号us(t)都是平稳的,且hsr(τ;t)在相干时间内保持不变,则接收信号yr(t)的自相关函数Rr(m)可以表示为

(2)

式中,Rs(m)为主用户s信号的自相关函数;Rhsr(τ;m)为信道hsr(τ;t) 的自相关函数;αsr为信道增益;m为延迟时间.

由式(2)可知,自相关函数Rr(m)对应的接收信号功率谱为

Pr(f)=αsrPs(f)

(3)

进一步假设网络中存在Ns个主用户，且每个从用户接收机都受本地噪声影响，信道hsr(τ;t)与信号us(t)不相关，则从用户r的接收功率谱可表示为

(4)

频谱感知技术仅需要知道功率谱的粗略情况，故可利用如图1所示的基扩展模型[10]来近似主用户信号功率谱，即主用户信号功率谱可由带宽为B的Nb个不重叠单位矩形函数γv(f) 来表示，其具体表达式为

(5)

式中,θsv为模型系数;γv(f)为第v(v=1,2,…,Nb)个单位矩形函数.由于γv(f)相互不重叠,故可利用其将信号功率谱分为Nb个频段.

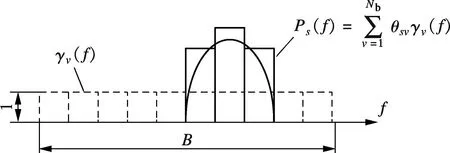
图1　信号功率谱的基扩展模型

将式(5)代入式(4)可得

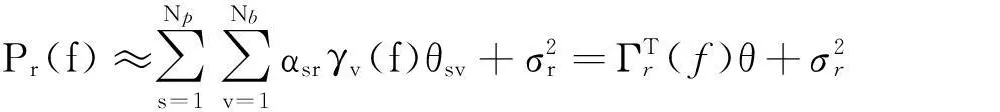
Pr(f)≈ ∑Nps=1∑Nbv=1αsrγv(f)θsv+σ2r=ΓTr(f)θ+σ2r

(6)

式中,θ={θ11,θ12,…,θNpNb}T为模型系数向量;Γr(f)={α1rγ1(f),α1rγ2(f),…,αNprγNb(f)}T.

由式(6)可知,当信道增益αsr已知时,可通过θ中非零元素所对应的v来确定主用户占用频段，并根据非零值大小来确定相应的发射功率.

(7)

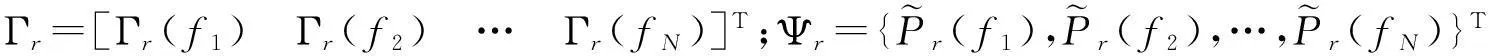
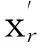
Ψ=Γθ+Kσ+ε

(8)

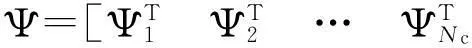
由于本地噪声未知,因此需将本地噪声向量σ和模型系数向量θ合并构成统一向量θ′,以便进行统一建模,即对式(8)进行如下变形:

Ψ=Γθ+Kσ+ε=Γ′θ′+ε

(9)

式中,Γ′=[ΓK],θ′=[θσ]T.

由此可知，本文可利用所提空间频谱分布协作感知算法来估计统一向量θ′，从而获得主用户占用频段、发射功率及其所处位置，并初步估计出本地噪声.

2空间频谱分布协作感知算法

变分贝叶斯推断技术是一种泛函近似方法，通过利用观测到的数据，获取统计模型中不可观测变量的近似后验概率[12-13].本文拟利用该技术设计出一种新型空间频谱分布协作感知算法,通过求解统一向量θ′的最优值,获得主用户所使用的频段、功率及其所处位置,并初步估计出本地噪声.

首先,由式(9)可知,全局功率谱模型的联合概率密度函数可表示为

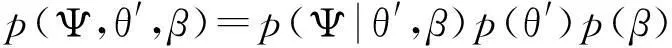
(10)

(11)

由此可知,共轭先验p(θ′)为高斯分布,而共轭先验p(β)为伽马分布,故

(12)

(13)

式中,χ′为统一向量θ′的误差精度参数向量;a0,b0为超参数.

由于χ′也是未知的,故可将其作为待估参数,则模型的联合概率密度函数可扩展为

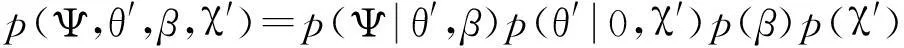
(14)

(15)

由此可推断出p(θ′),p(β)和p(χ′)的近似函数q(θ′),q(β)和q(χ′)分别为高斯分布、伽马分布和伽马分布,即

(16)

(17)

(18)

其次,q(β)的最优值q*(β)的计算公式为

lnq*(β)=Eθ′,χ′[lnp(Ψ,θ′,β,χ′)]+C=

(19)

式(19)为伽马分布的对数形式,故

(20)

(21)

lnq*(χ'n)= Eθ',β,{χ'iχ'i∈χ',χ'i≠χ'n}[lnp(Ψ,θ',β,χ')]+C=

(22)

式(22)为伽马分布的对数形式,故

(23)

(24)

q(θ′)的最优值q*(θ′)的计算公式为

lnq*(θ′)=Eβ,χ′[lnp(Ψ,θ′,β,χ′)]+C=

(25)

(26)

(27)

由式(26)和(27)可知，求解q(θ′)的最优值依赖于近似后验q(β)和q(χ′) 的取值.因此，需利用迭代算法对q(θ′)的最优值进行求解，即指定某近似后验，保持其他近似后验为前次最优值，从而求得该近似后验的本次最优值.通过反复的迭代运算，最终获得近似后验q(θ′)的最优值.

综上所述,可利用向量θ中非零元素对应的信道增益αsr获得主用户的近似位置坐标,根据非零元素对应的v来确认主用户的占用频段，并按照非零元素值大小来确定相应的发射功率.同时,可利用本地噪声向量σ得到每个从用户的本地噪声.

3仿真结果及分析

本文利用Matlab软件构建了仿真平台,并将仿真环境分为以下2种:① 高斯近似仿真环境,即将式(8)中的ε近似简化为加性高斯白噪声;② 真实仿真环境,即未对ε进行近似简化.本文所提算法是基于ε符合高斯分布的假设推导出来的,需在这2种仿真环境下对比该算法的性能,以验证其有效性.

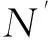
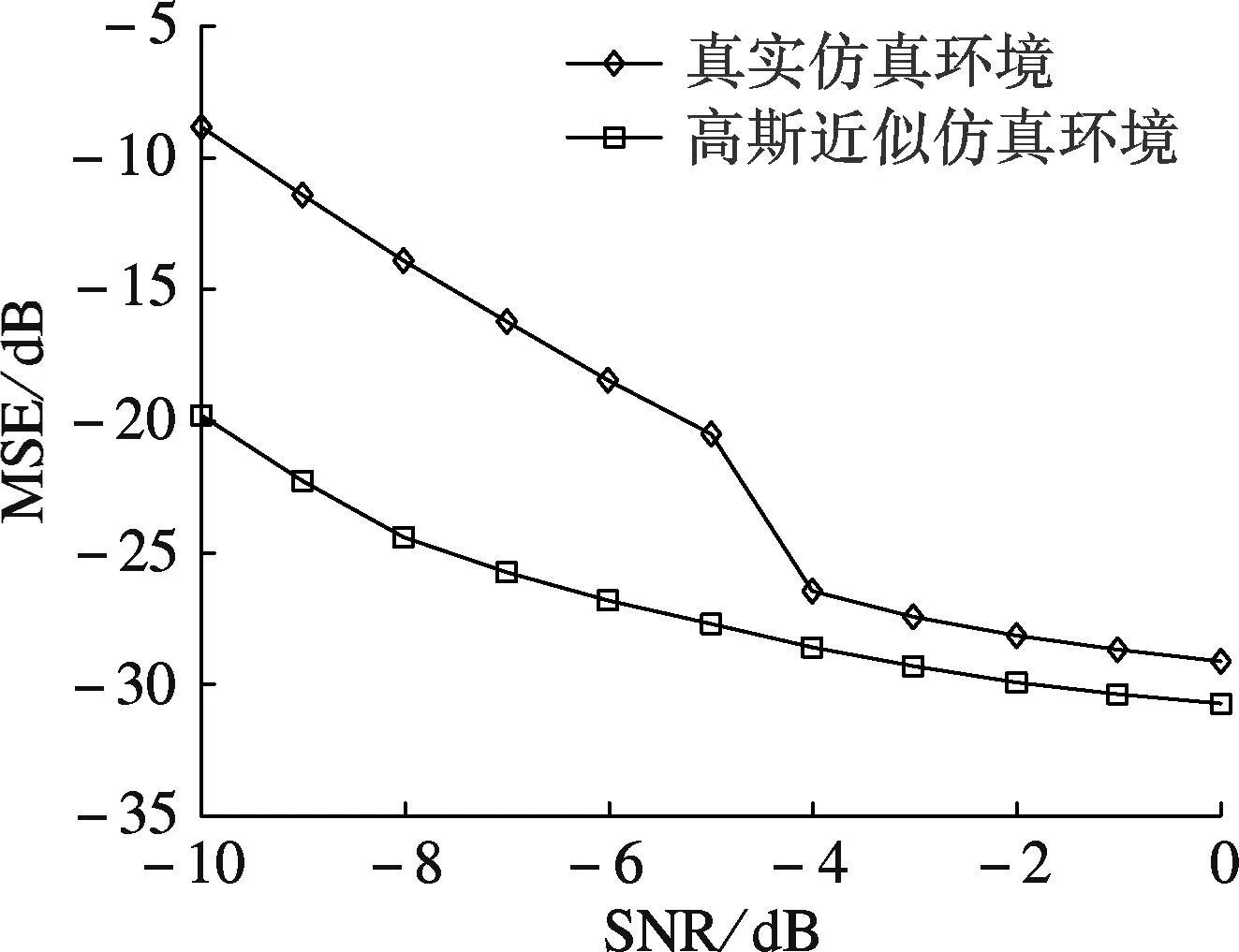
图2　均方误差曲线

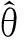
(a) 真实仿真环境

(b) 高斯近似仿真环境

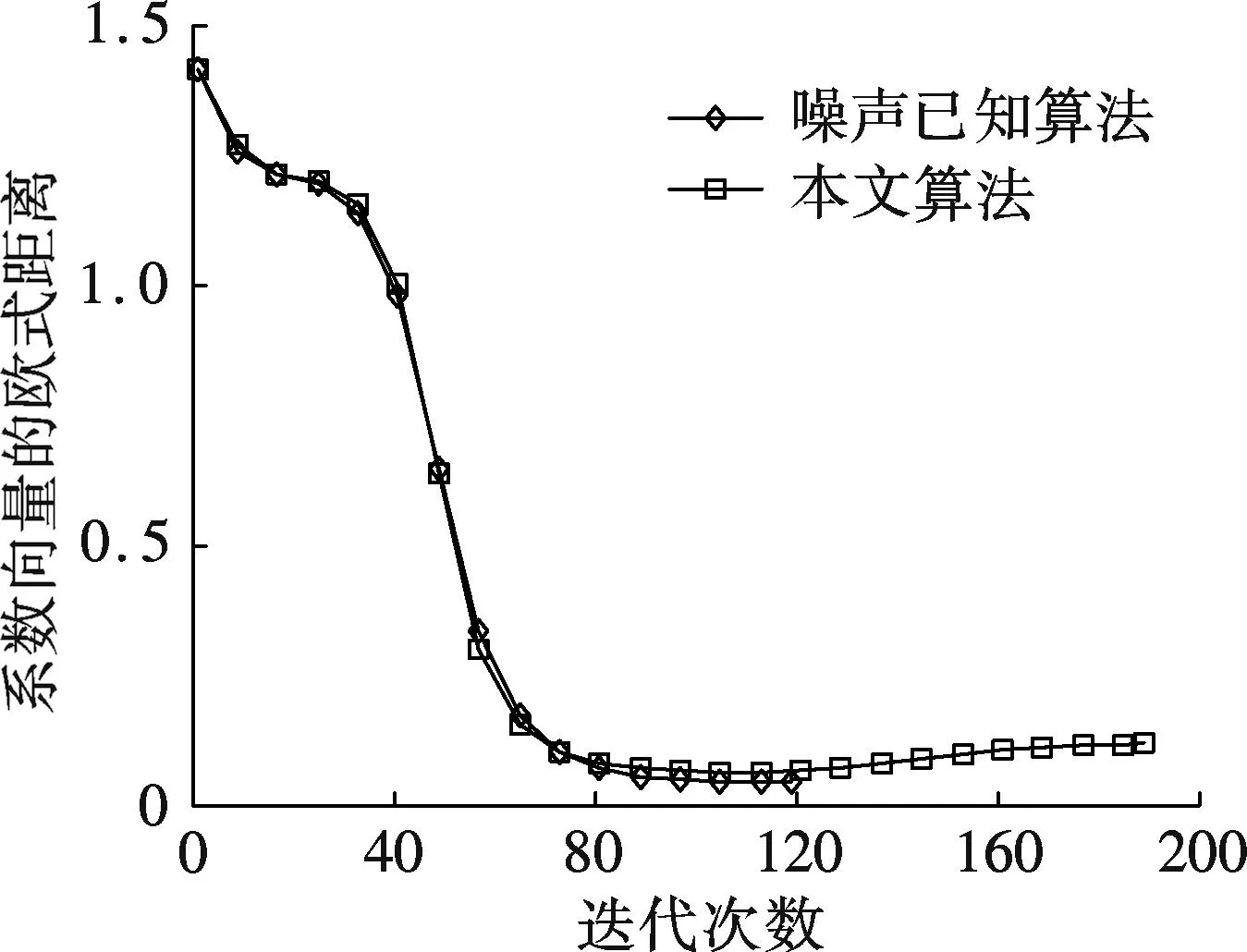
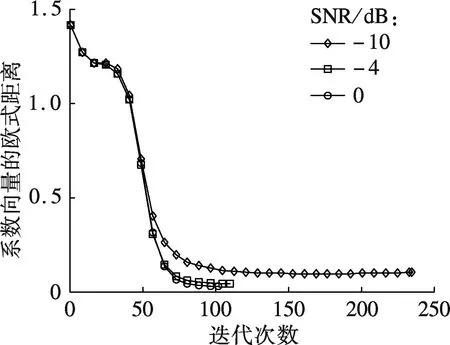
图4　噪声已知算法与本文算法的估计性能比较

最后,选择基于非负最小二乘(NNLS)准则的算法与本文算法进行均方误差性能对比.NNLS准则具体为

(28)

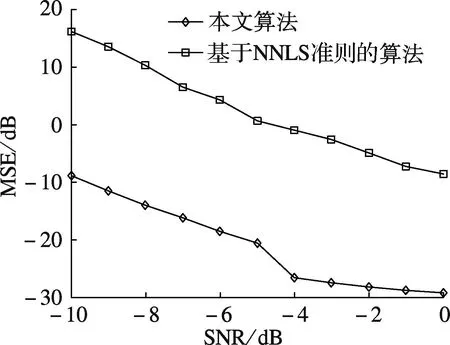
图5　基于NNLS准则的算法与本文算法的均方误差性能比较

4结语

本文考虑了本地噪声未知的情况,将本地噪声纳入全局功率谱模型进行统一建模，并在此基础上设计出噪声未知的空间频谱分布协作感知算法，以求得主用户占用频段、发射功率及其所处位置，初步估计出本地噪声.本文对2种仿真环境下的算法性能进行了对比,验证了所提算法的有效性,并分析其收敛稳定性.同时,证明了所提算法性能虽弱于噪声已知算法的性能,但相比基于非负最小二乘准则的算法具有更好的均方误差性能.

参考文献 (References)

[1]Goldsmith A, Jafar S A, Maric I, et al. Breaking spectrum gridlock with cognitive radios: An information theoretic perspective[J].ProceedingsoftheIEEE, 2009, 97(5): 894-914. DOI: 10.1109/JPROC.2009.2015717.

[2]Lu L, Zhou X W, Onunkwo U, et al. Ten years of research in spectrum sensing and sharing in cognitive radio[J].EURASIPJournalonWirelessCommunications, 2012, 2012: 28.

[3]Zeng Y H, Liang Y C, Hoang A T, et al. A review on spectrum sensing for cognitive radio: Challenges and solutions[J].EURASIPJournalonAdvancesinSignalProcessing, 2010, 2010(1): 381465. DOI:10.1155/2010/381465.

[4]Nishimori K, Taranto R D, Yomo H, et al. Spatial opportunity for cognitive radio systems with heterogeneous path loss conditions[C]//IEEEVehicularTechnologyConference. Dublin,Ireland, 2007: 2631-2635.

[5]Riihijarvi J, Mahonen P. Exploiting spatial statistics of primary and secondary users towards improved cognitive radio networks[C]//IEEE3rdInternationalConferenceonCognitiveRadioOrientedWirelessNetworksandCommunications. Singapore, 2008: 1-7.

[6]Min A W, Kim K H, Singh J P, et al. Opportunistic spectrum access for mobile cognitive radios[C]//2011ProceedingsofIEEEINFOCOMConference. Shanghai, China, 2011: 2993-3001.

[7]Caso G, Nardis L D, Holland O, et al. Impact of spatio-temporal correlation in cooperative spectrum sensing for mobile cognitive radio networks[C]//Proceedingsofthe10thInternationalSymposiumonWirelessCommunicationSystems. Ilmenau, Germany, 2013: 1-5.

[8]Paura L, Savoia R. Mobility-aware sensing enabled capacity in cognitive radio networks[C]//2013IEEEInternationalWorkshoponMeasurementsandNetworkingProceedings. Naples,Italy, 2013: 179-183.

[9]吴名,宋铁成,胡静,等.一种基于变分贝叶斯推断的新型全局频谱协作感知算法[J].通信学报,2016,37(2):115-123.

Wu Ming, Song Tiecheng, Hu Jing, et al. A novel cooperative global spectrum sensing algorithm based on variational Bayesian inference[J].JournalofChinaInstituteofCommunications, 2016, 37(2): 115-123.(in Chinese)

[10]Giannakis G B, Tepedelenlioglu C. Basis expansion models and diversity techniques for blind identification and equalization of time-varying channels[J].ProceedingsoftheIEEE, 1998, 86(10): 1969-1986. DOI:10.1109/5.720248.

[11]Cevher V, Duarte M F, Baraniuk R G. Distributed target localization via spatial sparsity[C]//EuropeanConferenceonSignalProcessing. Lausanne, Switzerland, 2008: 1-5.

[12]Girolami M. A variational method for learning sparse and overcomplete representations[J].NeuralComputation, 2011, 13(11): 2517-2532. DOI:10.1162/089976601753196003.

[13]Wipf D P, Owen J P, Attias H T, et al. Robust Bayesian estimation of the location, orientation, and time course of multiple correlated neural sources using MEG[J].NeuroImage, 2010, 49(1): 641-655. DOI:10.1016/j.neuroimage.2009.06.083.

Novel cooperative sensing algorithm for spatial spectrum distribution with unknown noises

Wu Ming Song Tiecheng Shen Lianfeng Hu Jing

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

Abstract:In order to obtain the global information including occupied frequency bands, transmitting powers of the primary users (PUs), locations and local noises, a model for the global power spectral density (PSD) of the PUs is constructed, and a novel cooperative sensing algorithm for spatial spectrum distribution with unknown noises is also proposed. By utilizing variational Bayesian inference (VBI) theory, the model coefficient vector and the local noise vector are estimated to obtain the global information. The simulation results show that the proposed algorithm has high accuracy and convergence stability with the high signal noise ratio (SNR). Though the performance of this algorithm is worse than that of the algorithm with known noises, but its mean square error (MSE) performance is better than that of the algorithm based on the non-negativity least square (NNLS) criterion.

Key words:cognitive radio; spatial spectrum distribution; cooperative spectrum sensing; variational Bayesian inference; sparsity

DOI:10.3969/j.issn.1001-0505.2016.02.001

收稿日期:2015-09-15.

作者简介:吴名(1981—),男,博士生;宋铁成(联系人),男,博士,教授,博士生导师,songtc@seu.edu.cn.

基金项目:国家自然科学基金资助项目(61201248,61271207,61372104).

中图分类号:TN914

文献标志码:A

文章编号:1001-0505(2016)02-0231-06

引用本文: 吴名,宋铁成,沈连丰,等.一种噪声未知的新型空间频谱分布协作感知算法[J].东南大学学报(自然科学版),2016,46(2):231-236. DOI:10.3969/j.issn.1001-0505.2016.02.001.