基于GM(1,1)模型的卫星钟差短期预报

杨超,张家荣,贾勇帅

(1.山东科技大学 测绘学院,青岛 266590;2.中国石油集团东方地球物理勘探有限责任公司,涿州 072751)

基于GM(1,1)模型的卫星钟差短期预报

杨超1,张家荣2,贾勇帅1

(1.山东科技大学 测绘学院,青岛 266590;2.中国石油集团东方地球物理勘探有限责任公司,涿州 072751)

摘要：卫星钟差的可靠预报对于高精度的卫星精密单点定位至关重要。由于卫星钟差对环境比较敏感,可将其看作灰色系统来处理。采用灰色系统理论的方法,建立GM(1,1)模型,用于卫星的短期预报。数据来自IGS的精密星历文件,研究了4颗卫星的钟差预报情况。结果表明,灰色系统理论在钟差预报方面有很大优势,预报精度在纳秒级。

关键词：GM(1,1);卫星钟差;短期预报

0引言

IGS分析中心提供GPS精密星历,卫星钟差精度可达0.1 ns,但须13 天后获取,无法满足实时精密单点定位的要求。为获取实时可靠的卫星钟差,许多学者对如何提高预报精度,建立高精度的预报模型进行了研究,并取得了显著效果,其中较常用的模型为二阶多项式模型。灰色系统理论由邓聚龙教授于20世纪80年代首次提出,该理论通过对原始数据的累加或累减生成新的数列进行建模,所需数据量少,建模速度快[1-2]。星载原子钟十分敏感,极易受外界及自身因素的影响,从而不能较好的掌握其复杂的变化规律[3]。因此可将该过程看作灰色系统,将灰色预测模型引入到卫星钟差预报中来[4]。GM(1,1)是一种很好的灰色预测模型,可有效减弱噪音和干扰。本文利用IGS精密星历建立GM(1,1)模型,分析预报结果的精度和可靠性。

1GM(1,1)建模过程和精度评定指标

1.1GM(1,1)模型建立

设有一原始序列 x(0)={x(0)(1),x(0)(2),…,x(0)(n)}为已知非负序列,经一次累加生成序列x(1)={x(1)(1),x(1)(2),…,x(1)(n)},其中x(1)(k)

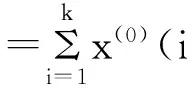
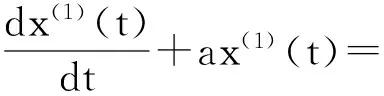
(1)

GM(1,1)模型的灰微分方程

x(0)(k)+az(1)(k)=u, k=2,3,…,n,

(2)

z(1)(k+1)=1/2(x(1)(k)+x(1)(k+1))

k=1,2,…,n-1,

(3)

将式(2)变形得:

L(n)=AX,

(4)

式中: L(n)观测数据; A为设计矩阵; X为待辨识参数。由最小二乘求解得:

X=(ATA)-1ATL(n).

(5)

将求得的a、u带入式(1),取初始值为x(0)(1),得x(1)的时间响应函数为

(6)

1.2GM(1,1)模型精度评定

由GM(1,1)模型得到:

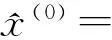
(8)

可得残差:

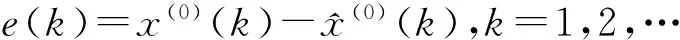
(9)

计算原始数列和残差的方差:

(10)

(11)

在式(10)和式(11)中,

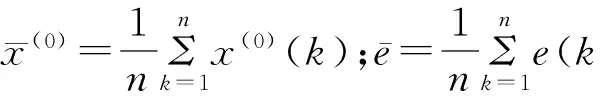
由S1和S2可得后验比值:

(12)

根据式(9)得小误差概率:

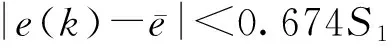
(13)

由C和P值可以确定模型的精度等级,具体等级情况如表1所示。

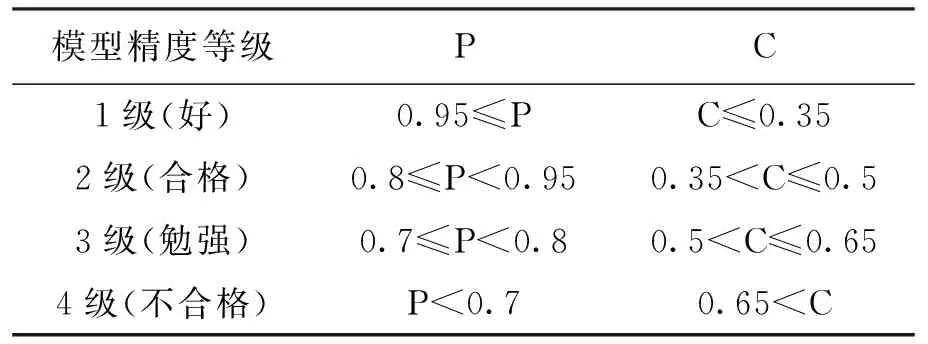
表1　模型精度等级

2算例与分析

本次试验数据来自IGS精密星历文件igs18650.sp3和igs18651.sp3,选取数据较具代表性的PRN4(BLOCKⅡARb)、PRN14(BLOCKⅡRRb)、PRN24(BLOCKⅡF-3Cs)和PRN31(BLOCKⅡR-MRb)卫星钟为研究对象。选取2015年第277个年积日的后24个历元的数据建模,预测第278年积日的卫星钟差,并与精密星历文件中的数据对比[5-8]。经过计算可得四颗卫星的GM(1,1)时间响应函数分别为

281737，

302511，

57708，

455.5172.

模型精度和外推预报结果的精度结果如表2所示。

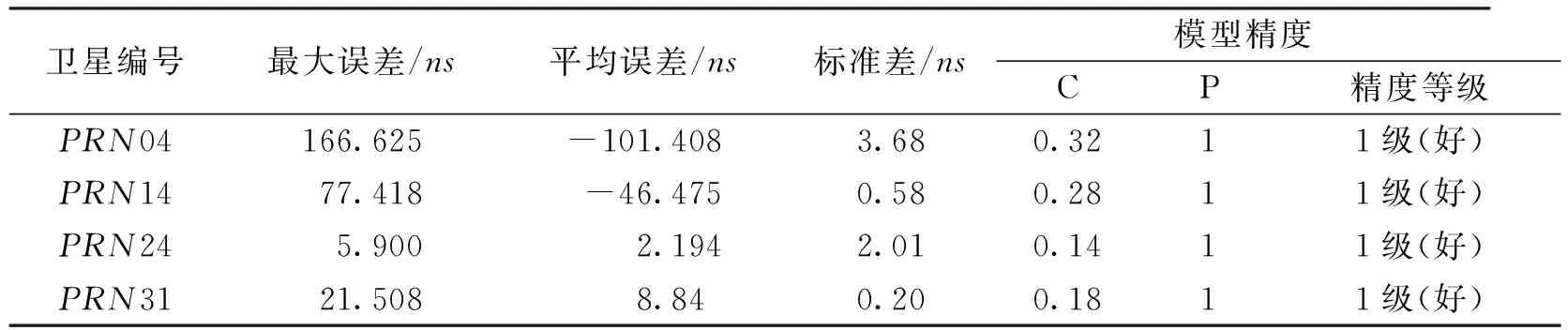
表2　模型精度及外推预报值精度评定

两颗卫星的预报结果和误差如图1和图2所示。

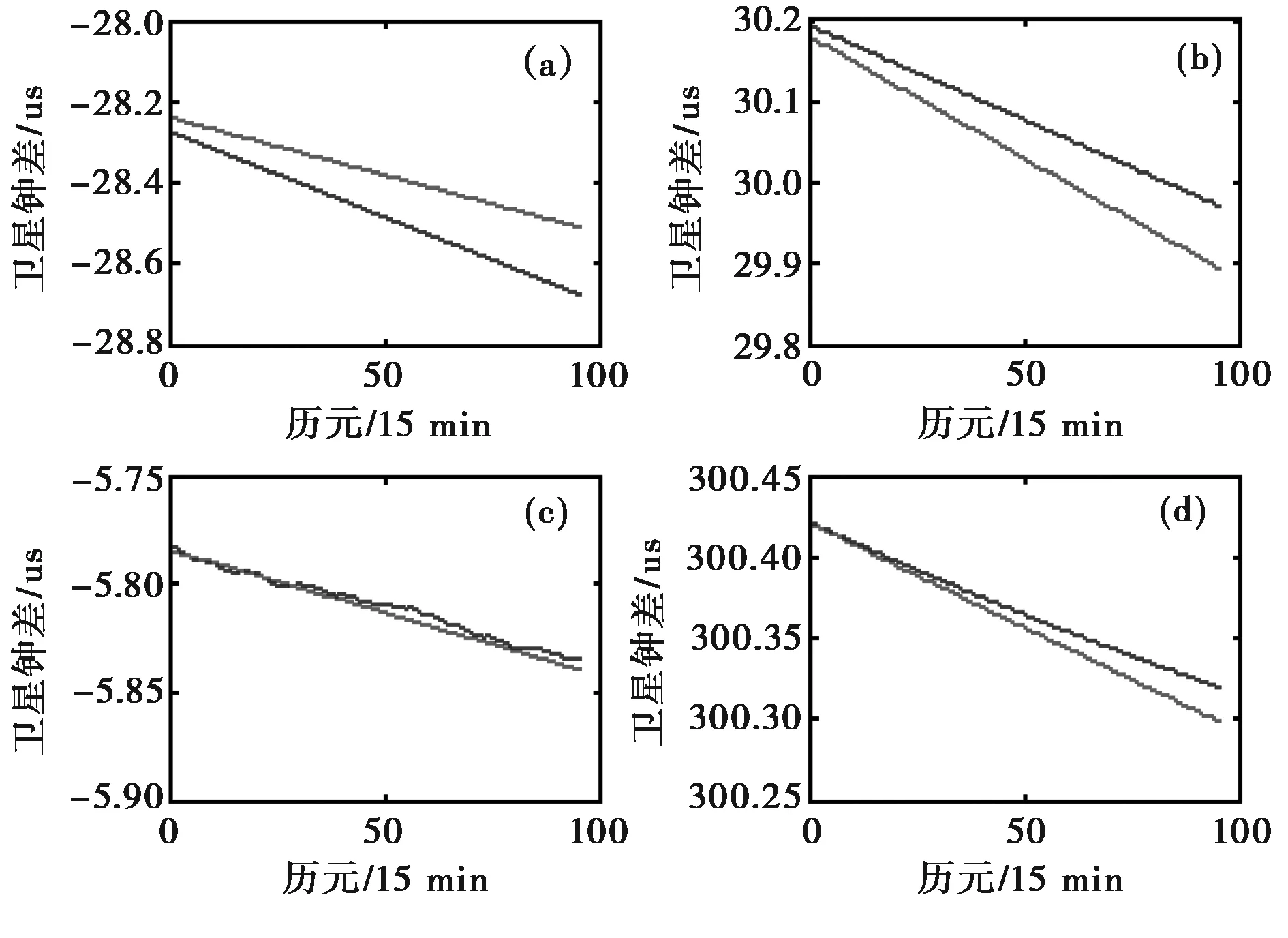
图1　预报效果 (a) PRN4; (b) PRN14; (c) PRN24;　　　 (d) PRN31

通过以上分析可以得出:

1) 灰色预测模型的模型的模型精度比较理想,属于1级;

2)GM(1,1)模型对四种卫星钟的钟差外推精度在ns级,BLOCKⅡR-MRb的预报精度最高,为0.2ns;

3)GM(1,1)模型对PRN4、PRN14的预报结果不理想,平均误差较大。

3结束语

通过第277年积日精密星历后6个小时(24历元)的卫星钟差为原始数据,建立灰色系统模型,预报278年积日的卫星钟差。试验中4颗卫星的钟差用GM(1,1)模型进行预报,分析结果表明,预报精度不但与模型有关,还与原子钟类型密切相关。本次试验中对BLOCKⅡACs钟差预报精度较高,在ns级。下一步可分析原子钟的钟差数据特点,选择更加优化的预测模型进行分析,如对灰色模型的背景值和初始值改进,来减小系统误差,提高精度。

参考文献

[1] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.

[2] 唐万梅.几个预测方法及模型的研究[D].呼和浩特:内蒙古大学,2006.

[3] 崔先强,焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报·信息科学版，2005,30(3):447-449.

[4] 郑作亚,陈永奇,卢秀山.灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J].天文学报，2008,49(3):306-319.

[5] 李玮,程鹏飞,秘金钟.灰色系统模型在卫星钟差短期预报中的应用[J].测绘通报，2009(6):32-35.

[6] 宋倩,韩春好.抗差灰色模型及其在卫星钟差预报中的应用[J].测绘科学技术学报，2013,30(5):471-474.

[7] 季善标,朱文耀,熊永清.精密GPS卫星钟差的改正和应用[J].空间科学学报，2001,21(1):42-47.

[8] 路晓峰,杨志强，贾小林,等.灰色系统理论的优化方法及其在卫星钟差预报中的应用[J].武汉大学学报·信息科学版，2008,33(5):492-495.

杨超(1989-),男,硕士生,主要研究方向为卫星定位与导航。

张家荣(1990-),男,助理工程师,主要从事石油物探测量方面的工作。

贾勇帅(1991-),男,硕士生,主要从事变形监测方面的研究。

Based on the GM(1,1)Model for Predicting the Short-Term Satellite Clock Error

YANG Chao1,ZHANG Jiarong2,JIA Yongshuai1

(1.GeomaticsCollege,ShandongUniversityofScienceandTechnology,Qingdao266590,China;2.BGPINC.,ChinaNationalPetroleumCorporation,Zhuozhou072751,China)

Abstract: It’s important for precise point positioning to predicting the satellite clock error. As the clock error is sensitive to the environment, we can consider it as grey model to dealing with. In the paper, we try to using the GM(1,1)model to forecasting the clock error. The date for building the model comes from IGS’s SP3 file. In the test, we study four satellite clock errors. The results show that gray system has an advantage in predicting the clock error. The predicting accuracy is in ns scale.

Keywords:GM(1,1); satellite clock error; short-term prediction

doi:10.13442/j.gnss.1008-9268.2016.02.017

收稿日期：2015-12-24

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0089-03

作者简介

联系人： 杨超 E-mail: yangchaoch29@126.com