对流层映射函数对PPP精度因子影响

刘惠涛,熊永良,薛骐

(西南交通大学 地学学院测量工程系,成都 611756)

对流层映射函数对PPP精度因子影响

刘惠涛,熊永良,薛骐

(西南交通大学 地学学院测量工程系,成都 611756)

摘要：精密单点定位(PPP)精度因子分析对于坐标和对流层估计精度预测具有重要意义。本文利用IGS提供的精密星历文件计算并分析了不同对流层映射函数对精密单点定位中对流层天顶方向湿延迟估计的精度因子的影响以及当对流层延迟能够精确用模型改正时精密单点定位精度因子的大小。采用Chao映射函数模型估计出的对流层天顶方向湿延迟的精度最高而使用Ifadis映射函数模型估计出的对流层天顶方向湿延迟的精度最低。当对流层延迟能用模型改正(四参数)时,精密单点定位的位置精度因子和钟差精度因子将显著减小,其中接收机钟差精度因子减小最明显,Y方向精度因子次之。

关键词：精密单点定位;对流层延迟;映射函数

0引言

在GPS数据处理中,影响GPS用户位置解算误差的因素除了GPS信号测距的误差,还有卫星的几何结构,称作几何精度因子(GDOP)[1-3]。几何精度因子代表的是GPS测距误差造成的接收机与空间卫星的距离矢量放大系数[4]。通常意义上,它包括X、Y、Z分量的精度因子和时间精度因子。通过几何精度因子乘以单位权中误差,可以在外业前评价外业后可能达到的精度[1-3]。在需要进行高精度的观测时,通常利用星历预报软件选择PDOP值小于 3 的最佳观测时段,可以大大提高工作效率,避免不必要的时间耗费。在前人的研究中,通常是对伪距单点定位进行的研究,其精度不高。精密单点定位采用载波相位观测值,利用精密卫星星历和卫星钟差进行精密坐标、接收机钟差和对流层延迟估计。影响精密单点定位参数估计精度的主要因素包括卫星几何构型和对流层映射函数。

本文从理论上对精密单点定位精度因子进行分析。由于精密单点定位中,对流层湿延迟难以准确估计,只能作为一个参数进行解算,故本文中的精度因子包括:几何精度因子和对流层天顶方向湿延迟精度因子。而在对流层湿延迟的估计中,涉及不同的映射函数模型(Chao模型、Hopfield模型、Ifadis模型)[5-8],本文分析了不同映射函数对对流层天顶方向湿延迟精度因子的影响以及与传统的四参数(不将对流层湿延迟作为参数)解算的精度因子进行对比,并得到了有益的结论。

1精密单点定位数学模型及对流层映射函数模型

1.1精密单点定位数学模型

精密单点定位是指用户使用单台双频接收机接收数据,利用IGS数据中心提供的卫星精密星历和精密钟差进行处理的一种定位模式。在精密单点定位中常用的观测量为消电离层组合观测量:

(1)

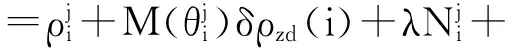
c(dti-dtj)+λεφ,

(2)

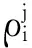
对流层延迟可分为对流层干延迟和对流层湿延迟,其中对流层干延迟能够准确估计而由于大气中水汽分布不均匀[9-10],常将对流层湿延迟作为一个独立参数进行估计,文中所涉及的对流层延迟无特殊标识均为对流层湿延迟。若仅考虑接收机钟差、对流层延迟,将式(1)线性化得到式(3):

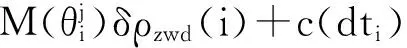
(3)

若:

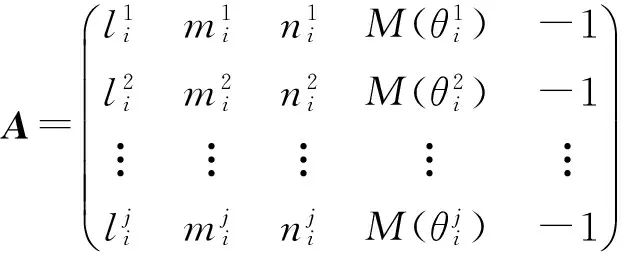
(4)

Q=(ATA)-1=

(5)

(6)

精度因子(DOP)表示误差的族大倍数。它是式(5)矩阵中的主对角线上的元素,分别表示XDOP、YDOP、ZDOP、TDOP、TropDOP.

1.2对流层映射函数模型

在精密单点定位中,斜向对流层延迟无法准确估计,斜向对流层延迟通常表示为天顶方向的对流层折射量与映射函数之积,给出三种映射函数模型:Chao模型[7]、Hopfield模型[1]、Ifadis模型[8]。

1.2.1Chao映射函数模型

Chao模型提出的是一个二项式连续函数的模型,其系数来自无线电探空资料所得到的结果。其表达式为

(7)

式中:i=dry时为干延迟;a1=0.00143;b1=0.00035;i=wet时为湿延迟;a2=0.0445;b2=0.0170;E为卫星高度角。

1.2.2Hopfield映射函数模型

Hopfield利用全球平均资料,总结出干大气层高度、湿大气层高度和大气折射率的误差模型,映射函数简单地表示为

(8)

式中:r为信号传播路径上某点到地心之间的距离;z0为信号源以测站点为圆点的天顶距。

1.2.3Ifadis映射函数模型

Ifadis模型是在大范围全球性的观测站和不同的气候条件下提出的,该模型总共收集了47个全球站的有关相对湿度、气压、温度、风速和方向的资料。Ifadis模型有三项展开式的形式和四项展开式的形式。Ifadis的全球性模型为

(9)

式中:

当i=dry时,

a=0.1237·10-2+0.1316·10-6(P0-

0.1378·10-5(T0-15);

b=0.3333·10-2+0.1946·10-6(P0-

0.1040·10-6(T0-15);

c=0.078.

(10)

当i=wet时,

a=0.5236·10-3+0.2471·10-6(P0-

0.1724·10-6(T0-15);

b=0.1705·10-2+0.7384·0-6(P0-

0.3767·10-6(T0-15);

c=0.05917.

(11)

式中: P0为地表大气压(hPa); T0为地表温度(°C); e0为地表水汽分压(hPa).

2实验分析

在1.1节模型中,当观测值文件经过各项误差改正,模糊度参数正确固定后,参数解算的精度主要与卫星的几何分布以及对流层延迟参数的影响系数有关。

本文中选择2013年11月12日的精密星历文件以30s为内插的时间间隔内插出0～12h的数据,共获得1 440个历元的数据。选择成都市某点作为作为接收机位置坐标,由于卫星高度角对精度因子存在一定影响,当卫星高度角设置的较大时,卫星观测的数据将会较少,卫星的图形交会强度较弱,会导致求出的精度不高,卫星的高度角设置的较小时,许多误差(如多路径误差、对流层延迟)将无法准确计算也会给结果造成不良影响,因此本文选择了10°高度角。

2.1四参数与五参数精密单点定位各精度因子对比

在本次实验中,对考虑对流层参数和不考虑对流层参数进行分析,研究二者的XDOP、YDOP、ZDOP和TDOP大小变化。对于五参数的精密单点定位,本实验采用的对流层映射函数为常用的Hopfield映射函数,最终结果如图1所示。

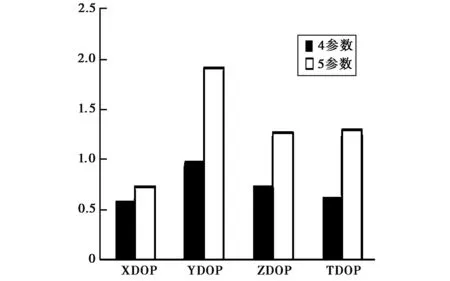
图1　四参数与五参数各精度因子平均值

由图1可知,四参数的各精度因子整体上都比五参数各精度因子小,即当对流层延迟能够用已知模型准确改正的条件下,精密单点定位参数的估计精度有所提高。其中TDOP的变化比例最大,五参数的接收机钟差精度因子比四参数的接收机钟差精度因子大52.1%,其次是YDOP,五参数的Y坐标精度因子比四参数Y坐标精度因子的大48.5%,然后是ZDOP,五参数Z坐标精度因子比四参数Z坐标精度因子大41.2%。变化最小的是XDOP,五参数比四参数X坐标精度因子大19.2%。这就说明,在精密单点定位中,对流层延迟项是否用已知模型准确估计,对接收机钟差精度因子的影响是最大的,而对X坐标精度因子的影响是最小的。

2.2不同对流层映射函数模型对对流层天顶方向延迟精度因子的影响

在观测方程中,分别采用文中所涉及的三种对流层延迟的映射函数进行分析,所得结果如图2所示。

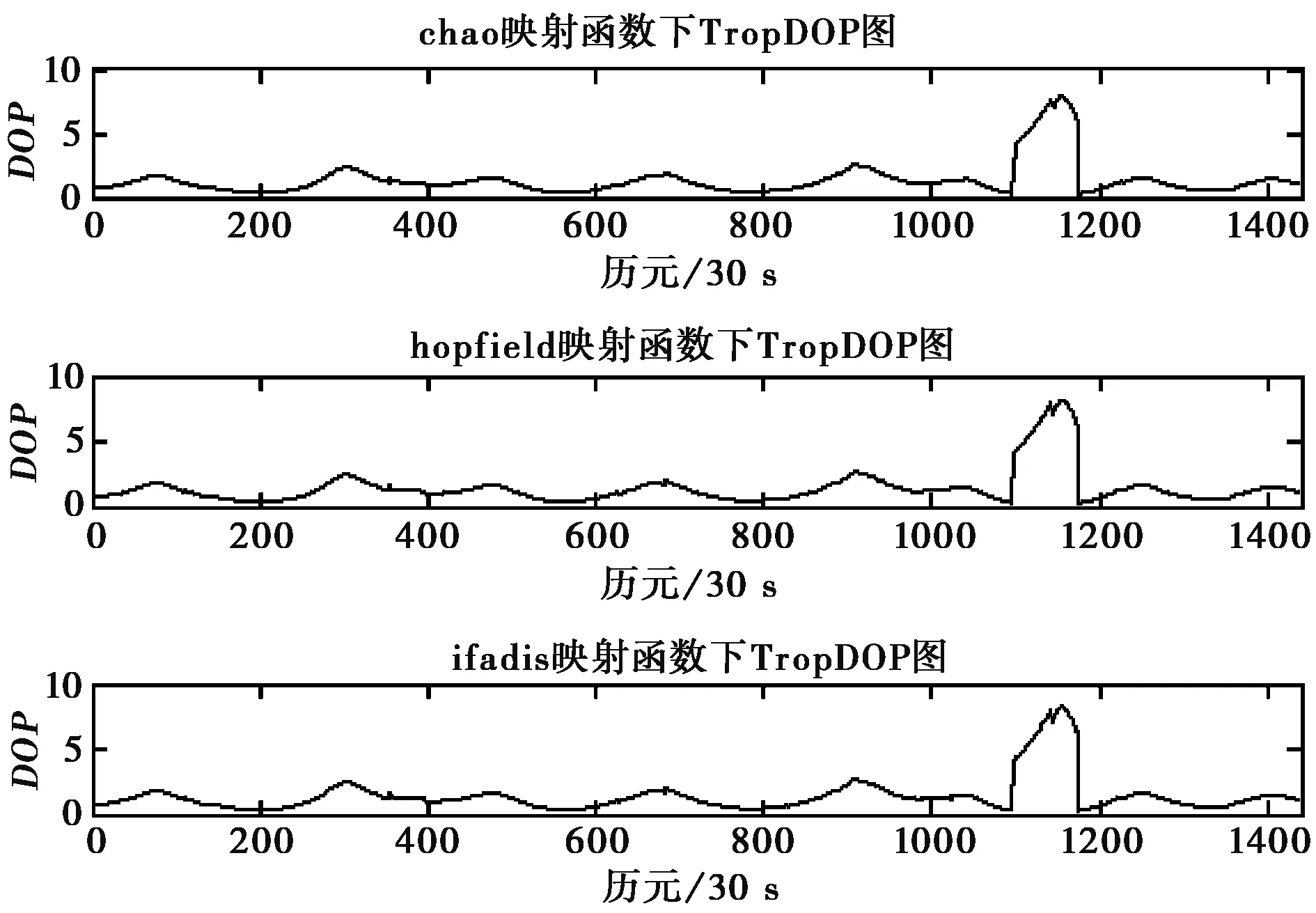
图2　不同映射函数下对流层天顶方向延迟DOP

从图2可以看出,不同对流层映射函数对于反演对流层天顶方向延迟量的趋势是相似的,但是从表1可以看出,Chao函数模型的对流层天顶方向延迟精度因子平均值最小,而Ifadis函数模型的对流层天顶方向延迟精度因子平均值最大,即Chao函数模型所求出的对流层天顶方向延迟估计精度最好,而Ifadis函数模型所求的对流层天顶方向延迟估计精度最差。

表1　不同映射函数下对流层天顶方向

3结束语

本文介绍了精密单点定位精度因子的计算过程以及三种常用的对流层映射函数模型,并对上述两个实验进行了分析。当精密单点定位解算过程中不加入对流层延迟参数时即对流层能够事先用已知模型进行改正,可以提高位置与接收机钟差的估计精度,其中对接收机钟差的估计精度提高最明显。在比较使用Chao模型、Hopfield模型和Ifadis模型进行对流层天顶方向湿延迟估计时,发现使用Chao模型时,对流层天顶方向湿延迟的估计精度因子最小即精度最高,这对以后在进行GPS水汽反演问题分析上,选取合适对流层映射函数模型有一定的作用。

参考文献

[1] 黄丁发,熊永良,周乐韬等.GPS卫星导航定位技术与方法[M].北京：科学出版社,2009.

[2] 叶世榕,张双成,刘经南. 精密单点定位方法估计对流层延迟精度分析[J]. 武汉大学学报·信息科学版,2008,33(8):788-791.

[3] 李鹏. GPS精密单点定位若干关键问题研究[D].成都:西南交通大学,2008.

[4] 胡稳才,张杏谷,黄丽卿. 全球定位系统的几何精度因子[J]. 大连海事大学学报,2002(4):42-45.

[5] ZHANG Y J, CHRIS G B. A real-time meteorological-based troposphere (RMT) correction with integrity bound for long baseline DGPS [J]. GPS Solutions,2005(9): 255-272.

[6] YOUNES S A,ELMEZAYEN A G.A comprehensive comparison of atmospheric mapping functions for GPS measurements in Egypt[J]. Journal of Geodetic Science, 2012,2(3): 216-223.

[7] CHAO C C. A new method to predict wet zenith range correction from surface measurements[R]. Jet Propulsion Laboratory, Pasadena, CA, JPL Technical Report 32-1526, vol XIV, 1973:33-41.

[8]IFADIS I I.The atmospheric delay of radio waves: modeling the elevation dependence on a global scale[R]. 1986.

[9] 叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学,2002.

[10]包海. GPS精密单点定位中对流层延迟改正模型的研究与分析[D].长沙:中南大学,2008.

刘惠涛(1992-),男,江西南昌人,硕士,主要研究方向为精密单点定位。

熊永良(1964-)，男，四川泸州人，博士生导师，主要研究方向为GPS精密定位定轨理论与应用及GNSS大气建模及气象应用。

薛骐(1991-)，男，黑龙江哈尔滨人，硕士生，主要研究方向为GNSS大气建模。

Different Troposphere Mapping Function's Effect on the Dilution of Precision of Precise Point Position

LIU Huitao,XIONG Yongliang,XUE Qi

(FacultyofGeosciencesandEnvironmentalEngineering,SouthwestJiaotongUniversity,Chengdu611756,China)

Abstract: The dilution of precision analysis of precise point position is significant for prediction of coordinate and troposphere estimation. In this paper, the effect of different tropospheric mapping function to the PPP dilution of precision is investigated and the magnitude of the PPP dilution of precision is analyzed if the tropospheric delay can be accurately modeled. When the zenith tropospheric wet delay is estimated, the most precise model is Chao mapping function and the Ifadis mapping function is the most imprecise. If the tropospheric delay can be modeled, the dilution of precision about position and receiver clock error would significantly reduce, and the precision of receiver clock error is improved the most obviously.

Keywords:Precise point position; tropospheric delay; mapping function

doi:10.13442/j.gnss.1008-9268.2016.02.021

收稿日期：2015-10-12

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0106-04

作者简介

资助项目: 国家自然科学基金(批准号:41274044)

联系人：E-mail:lht_2015@126.com