奔福德定律与舞弊审计
2016-06-21张苏彤


【摘 要】 奔福德定律(Benfords Law)是早在1881年就被偶然发现的一个古老而奇妙的数学定律。该定律揭示了序数0—999在不同数位上出现的概率分布规律。文章在简述这一古老数学定律的发展历程与基本内容的基础上,利用 “人为造假”的样本数据与随机数样本数据对该定律进行测试,证明了奔福德定律在舞弊侦测方面的有效性,并就该定律以及与之相关的数值分析技术在我国的运用等问题谈了看法,认为奔福德定律在识别“人为造假”数据方面具有明显作用,可以将奔福德定律及其相关的数值分析工具视为“财务舞弊检验器”,将其纳入我国的审计理论与方法体系,丰富我国在现代信息技术环境下应对高智能财务舞弊与经济犯罪的侦测手段。
【关键词】 奔福德定律; 舞弊审计; 测试; 虚假数据; 随机数
中图分类号:F233;D918.95 文献标识码:A 文章编号:1004-5937(2016)12-0007-09
引 言
近年来经济领域的犯罪与舞弊问题在我国日趋严重,对这些问题的查证需要不断完善与发展舞弊审计技术与手段。在各种舞弊审计与审计的方法中,分析性复核被认为是最为重要的工具。但是目前审计人员能够使用的分析性复核方法极为有限,主要局限于趋势分析、比率分析等传统方法,这些方法在应对日益隐蔽与高智商化的财务舞弊时常显出不适应的方面。奔福德定律在舞弊侦测领域的运用被认为是分析性复核方法在现代信息技术环境下有益的补充,因而结合我国的实际情况对其进行深入研究具有重要的现实意义。
在过去的半个多世纪中,国外大约有150篇与奔福德定律相关的学术论文发表。特别是自从美国审计准则公告第99号(SAS 99)[1]发布以来,越来越多的研究者开始关注奔福德定律在舞弊审计领域运用及其相关实务问题的解决。比如有文献报告了如何运用奔福德定律的理论检测在交易数据中隐藏的舞弊[2—3];如何有效运用奔福德定律在会计数据中侦测舞弊的思路与方法[4];如何将奔福德定律作为数值分析技术与分析性程序相结合提高注册会计师查证舞弊的技能的问题[5—6]。随着计算机辅助审计技术的快速发展,探讨如何将基于奔福德定律理论的数值分析技术嵌入计算机辅助审计软件以及如何借助于软件工具进行舞弊审计成为新的热点[7]。
在国内,迄今为止可以检索到十多篇有关奔福德定律及其应用的论文。其中《奔福德定律:一种舞弊审计的数值分析方法》[8]是最早将奔福德定律介绍到国内的论文之一,该文除了介绍这一定律给国内读者以外,还利用2003年1 394家上市公司公布的财务数据对奔福德定律进行了验证性测试。张苏彤和唐智慧[9]的《信息时代舞弊审计新工具:奔福德定律及其来自中国上市公司的实证测试》进一步对1 447家上市公司公布的2006年度的财务数据进行了验证性分析,并且对已经被证实实施了会计造假的上市公司的会计报表数据进行了测试,提出了以奔福德定律测试过程中形成的“相关系数”可以作为“财务舞弊测试器”的观点。近年来国内发表的相关论文主要还停留在科普性的介绍与理论上的测试与探讨层面[10],仅有少部分论文论及奔福德定律的舞弊检测方法[11]以及运用奔福德定律的理论对上市公司的虚假会计报表、财务舞弊等问题进行实证分析[12—13]。总体来看,我国对奔福德定律及其在舞弊审计领域的运用还处于理论上探讨与科普性介绍阶段,缺乏对策。
本文的主要贡献在于首次运用“人为造假”样本数据与随机数样本数据对奔福德定律进行了全面的测试,证明了奔福德定律在舞弊识别上的有效性。
一、奔福德定律:描述序数在不同数位上概率分布的奇妙数学定律
(三)适合奔福德定律数据的条件
并非所有的数据都符合奔福德定律,符合奔福德定律的数据一般应满足以下条件[19]:
1.数据应该是以某种方式涉及或从属于某种现象,换句话说,是由于某种原因(某一现象或事件)而导致发生的数字。比如,股票价格的形成要受到股票市场、与经济和金融环境有关的竞争力影响。
2.数据没有最大值或最小值的限制,比如人的年龄、人的体重、人的身高、田径运动员100米跑的成绩、小时工资额等。
3.数据完全应该是自然发生,不能是人为预先安排有特定含义的数字,如电话号码、身份证号、股票代码、社会保险号等,也不能是人头脑中想出来的数字,如ATM自动取款机上的取款金额。
4.数据既不能是完全随机数,也不能是有规律的数列。
5.数据的形成受多种因素综合作用,尤其适合分别来自两个以上系统的数据再经过一定运算后形成的数据。
二、对奔福德定律的实证测试:基于“人为造假”与随机数样本数据
(一)样本数据及其来源
为了加深对奔福德定律的认识,全面了解“人为造假”数据的统计学特征,并验证奔福德定律在识别财务舞弊方面的有效性,笔者利用近年来面对面给各类学员授课的机会先后请了321名学员以财务造假者的心态书写了6组总数为9 630个“人为造假”数据,这些数据的收集情况见表1。
为了进行对比分析,笔者利用Excel 2007的随机数发生器,运用函数“RANDBETWEEN(BOTTOM,TOP)”分别在100—999、100—9 999、100—99 999、100—999 999、100—9 999 999和100—99 999 999的范围内生成了6组,每组5 000个随机样本数据。这些数据的情况见表2。
(二)测试假设
假设1:“人为造假”样本数据的首位数、第二位数、前二位数的概率分布与奔福德定律理论值存在显著差异;
假设2:随机数样本数据的首位数、第二位数、前二位数的概率分布与奔福德定律理论值存在显著差异;
假设3:“人为造假”的首位数、第二位数、前二位数的概率分布与随机数不存在明显差异,“人为造假”数据可以视同为随机数;
假设4:造假者编造的虚假会计数字具有某些统计学上的特征或固有的书写习惯与偏好。
(三)测试结果
1.首位数测试
表3、表4分别给出了“人为造假”样本数据与随机数样本数据的首位数概率分布值以及与奔福德定律的比较。
由表3可见,“人为造假”样本数据的首位数概率分布与奔福德定律理论值存在显著的差异。从相关系数来看,6组“人为造假”的样本数据均与奔福德定律理论值呈弱正相关关系,其相关系数在0.96184—0.34686之间,其平均值的相关系数为0.92752。此项测试支持假设1。
由表4可见,6组随机数的首位数概率分布均与奔福德定律理论值呈负相关,其平均相关序数为-0.48321。序数1—9在6组随机样本数据的首位数上分布的概率均是围绕0.1111(即九分之一)上下波动,这样的概率分布是符合随机数的统计学特征的。此项测试支持假设2。
图1和图2直观地描述了“人为造假”与随机数样本数据首位数概率分布以及与奔福德定律理论值比较的情况。
由图1可以看出,“人为造假”的数据存在试图让1—9在首位数上均衡出现的趋势,但是相对随机数而言,其首位数分布概率远达不到均衡分布的程度;6组人为造假数据中的首位数“1”出现的概率最高,平均值为0.1946,但是仍达不到奔福德定律理论值的水平;“7”“8”“9”在首位数上出现的概率要高于奔福德定律理论值,且低于随机数的分布值。由此可以推测:造假者在编造虚假会计数字时,会不自觉地在首位数上多用一些“1”,而且会使以“7”“8”“9”开头的所谓大数字出现得多一些,这应该是造假者在蓄意编造虚假会计数字过程中不自觉显露出来的思维惯式。此项测试支持假设4。
表5列出了6组“人为造假”与6组随机数样本数据的首位数概率分布平均值之间的比较。
表5表明,“人为造假”样本数据与随机数样本数据首位数的概率分布均值存在显著差异,两者之间的相关系数为-0.53181,因此不能将“人为造假”数据与随机数视为等同。此项测试不支持假设3。
2.第2位数测试
表6、表7、图3、图4分别给出了“人为造假”样本数据与随机数样本数据的第二位数概率分布值以及与奔福德定律的测试结果比较。
由表6可知,就第二位数而言,6组人为造假的样本数据与奔福德定律理论值同样呈弱的正相关关系,其平均相关系数仅为0.5570。此项测试支持假设1。
由表7可见,6组随机数样本数据与奔福德定律理论值相比同样呈弱的正相关或负的相关关系,平均相关系数为0.4046。其显著特征为序数0—9在第二位数上分布概率在0.10±0.0175的范围内上下波动。此项测试支持假设2。
图3显示,“人为造假”数据在第二位数上与奔福德定律理论值差异最大的是“0”。在6组样本数据中,“0”在第二位数上出现的最高频率为0.5254,最低频率为0.1777,平均频率为0.3392,均比理论值高。由此可以推测:造假者会不自觉地在第二位数上多用“0”。此项测试结果支持假设4。
表8列出了“人为造假”样本数据与随机数样本数据在第二位数上概率分布均值的比较。表8表明,“人为造假”样本数据与随机数样本数据在第二位数的概率分布均值存在显著差异,两者之间的相关系数为0.0833,因此不能将“人为造假”数据等同于随机数。此项测试不支持假设3。
3.前二位数据测试
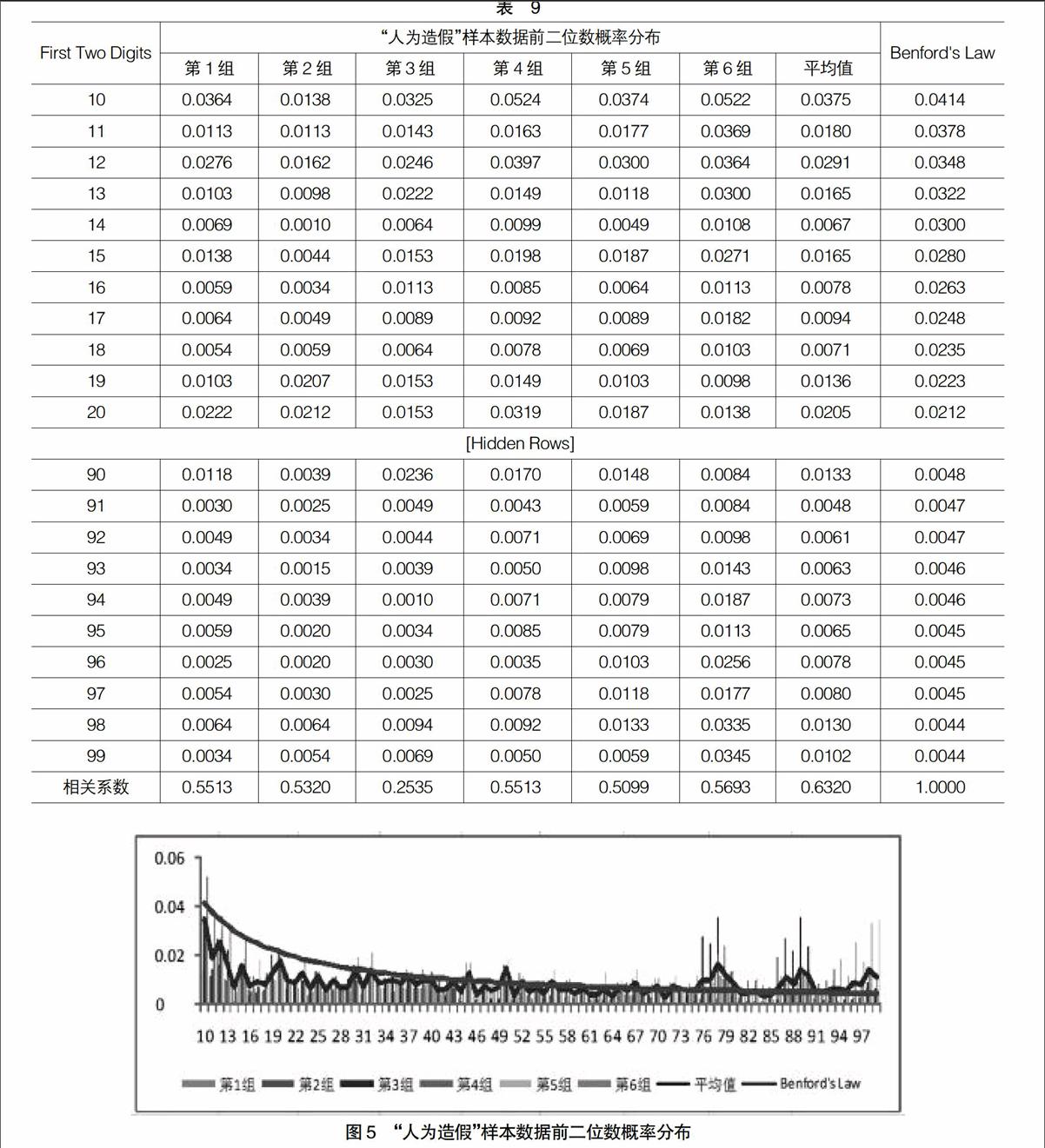
表9和图5分别列出了6组“人为造假”样本数据与随机数样本数据的前二位数概率分布情况。
由表9和图5可见(限于篇幅,图表中数据有删节):人为造假样本数据的前二位数概率分布与奔福德定律的理论值呈弱的正相关关系,6组样本数据中,相关系数最大值为0.5693,最小值为0.2535,平均相关系数为0.6320。此项测试为假设1的成立提供了证据支持。
由表10和图6发现(限于篇幅,图表中数据有删节):随机数样本数据前二位数的概率分布与奔福德定律的理论值存在弱的正相关关系,6组样本数据中,相关系数最大值为0.1185,最小值为-0.0758,平均相关系数为0.1441。其前二位数分布的特征为序数10—99均在范围为0.01±0.08上下波动。此项测试为假设2的成立提供了证据支持。
表11和图7列出了“人为造假”样本数据与随机数样本数据在前二位数上概率分布均值的比较。
由表11和图7可知,“人为造假”样本数据与随机数样本数据在前二位数的概率分布均值存在显著差异,两者之间的相关系数为0.1618,鉴于此,不能将“人为造假”数据等同于随机数。此项测试不支持假设3。
由图8可以观察到:“人为造假”样本数据的前二位数在71—98之间出现高于奔福德定律理论值的三个峰值,而且在10—25之间出现高于随机数均值且低于奔福德定律理论值的情况。由此可以推测:造假者在编造虚假会计数据时,有在10—25和71—98的区间上选择前二位数字的倾向。此项测试结果支持假设4。
综合上述对“人为造假”与“随机数”的测试分析结果可以得出以下结论:
第一,“人为造假”样本数据不论是首位数、第二位数还是前二位数的概率分布均与奔福德定律的理论值均存在显著差异,假设1在本次测试中得到证实。由此可以推论:只要是人为编造的数据,其首位数、第二位数和前三位数的概率分布很难出现与奔福德定律理论值一致的情况。
第二,“随机数”样本数据在首位数、第二位数、前二位数上的概率分布值与奔福德定律理论值同样存在显著差异,其显著的特征在于首位数、第二位数和前二位数的概率分别围绕均值0.1111、0.1000和0.0100波动。假设2在本项测试中得到证据支持。
第三,“人为造假”样本数据不论是首位数、第二位数,还是前二位数的概率分布均与随机数样本数据的相应概率分布值存在显著差异,假设3在本次测试中没有得到证明。鉴于此,不能简单地将人为编造的数据认同为随机数。
第四,舞弊者在编造虚假会计数字时存在某种共同的选择取向或固有的选择习惯,比如,他们会在首位数上多选择些“1”“7”“8”“9”,在第二位数上多用些“0”等。假设4在此次测试中得到支持,但并不充分。造假者编造虚假会计数字时对序数在不同数位上的选择取向有待深入研究。
此项测试结果很好地说明了奔福德定律在对“人为造假”数据识别的有效性,为我们利用奔福德定律侦测财务舞弊提供了重要的理论支持。
三、运用奔福德定律进行舞弊审计的启示与建议
通过对奔福德定律的深入研究与测试分析,可以得到如下启示:
第一,奔福德定律在舞弊审计领域的运用实际上是分析性复核方法在现代信息技术环境下的发展与有益的补充。传统的分析性复核方法是从财务数据的内在勾稽关系与逻辑上的合理性角度出发来发现会计错弊的。而奔福德定律的运用则是借助于现代计算技术从统计学的角度检测数字在不同数位上的概率分布规律,进而发现会计错弊的一种新型数值分析方法。奔福德定律在舞弊审计领域的运用丰富了舞弊审计的技术手段,加大了财务造假的难度,提高了舞弊审计工作的效率,丰富与发展了分析性复核方法体系。
第二,运用奔福德定律进行舞弊审计需要特别注意以下方面的局限性:(1)并不是所有的数据类型都适合奔福德定律,运用奔福德定律时要特别注意其限定性条件。(2)检测的样本数据与奔福德定律不相符并不说明一定存在舞弊,要注意排除样本数偏少、存在特定授权交易等情况。此外,样本数据与奔福德定律不相符只是存在财务舞弊的必要条件,只能说明存在舞弊的迹象或征兆,如果要证实舞弊的确存在,还需“顺藤摸瓜”“按图索骥”才能找到有效的证据。(3)检测的样本数据与奔福德定律相符并不说明一定不存在舞弊,尤其是在大样本数据的情况下,发生次数不多的舞弊数据会被淹没在大样本数据的“汪洋大海”之中而无法显现出来。此时,审计人员应该结合运用分层分析的方法将大样本“化整为零”。分层测试可以分很多种类,可以按样本的明细账户进行分层,可以针对不同的供货商、购货商进行分层,也可以根据不同购货地区、销售地区进行分层,还可以根据不同的季度甚至不同月份进行分层。
第三,运用奔福德定律进行舞弊审计还有一个重要的前提:造假者不知晓奔福德定律。在造假者不知晓奔福德定律的情况下,他们对财务数据的编造一般会存在这样的规律:(1)会不自觉地多选择一些以“1”为首位数的数字,但是首位数“1”的使用率达不到奔福德定律的理论值;(2)会有意识地多选择一些以“6”“7”“8”“9”开头的所谓大数字,特别是我国的造假者会偏爱“6”“8”“9”等吉祥数字;(3)会在第二位数上多用“0”。需要引起注意的是随着奔福德定律数值分析技术的广泛应用,对它了解的人会越来越多,造假者会注意到这一规律并会在造假时加以考虑。奔福德定律识别舞弊的有效性会随着人们对其知晓程度的提高而下降。
第四,可以将奔福德定律及其有关的数值分析工具视为“财务舞弊检验器”。利用奔福德定律,可以检测多种类型的财务舞弊,比如,在我国的证券市场中,对上市公司首次发行股票以及随后的增发、配股、ST(特别处理)与退市等都有严格的限制条件,很多企业会操控财务数据使之迎合政策界限的要求。借助于奔福德定律进行数值分析可以帮助我们透视数字背后隐藏的秘密,评价企业财务数据的质量,同时也可以给政府有关部门提供制定政策的科学依据。为此,建议我国有关部门研究推广奔福德定律的理论及其数值分析技术,将其纳入我国的审计理论与方法体系,进一步丰富我国在现代信息技术环境下应对高智能财务舞弊与经济犯罪的侦测手段。
第五,在舞弊审计中运用奔福德定律会涉及大量的统计分析工作,如果没有现代计算机技术的广泛运用,是不可能完成此项任务的。为解决这一现实问题,国外已经有人开发了专门的应用软件。许多国外公司开发的计算机辅助审计工具都将奔福德定律作为一个单独的模块嵌入其中,比如:ActiveDate for Excel、ACL、IDEA等,大大提高了工作效率。建议我国有关软件开发机构借鉴国外的相关经验,尽快开发出具有自主知识产权的奔福德定律应用软件工具。
结 论
1.人为造假的样本数据和完全随机数样本数据的首位数、第二位数、前二位数上的概率分布值与奔福德定律理论值存在显著差异;人为造假样本数据不论是首位数还是第二位数与前二位数的概率分布均与随机数存在显著差异,不能将人为编造的数据认同为随机数。
2.舞弊者在编造虚假会计数字时,对序数在不同数位上的选择存在某种共同的选择取向,研究并掌握造假者的数字选择取向对于识别财务舞弊有重要的意义。该方面的研究尚属空白,有待进一步发掘。
3.奔福德定律在识别“人为造假”数据方面具有明显作用,但在实际运用时要注意适用数据的条件和局限性。●
【参考文献】
[1] AICPA.Statement on Auditing Standards No. 99, Consideration of Fraud in a Financial Statement Audit [A].2002.
[2] WALLACE W. Assessing the quality of data used for benchmarking and decision-making[J].The Journal of Government Financial Management,2002,51(3):16-21.
[3] GORDON B M,COLIN O B. Using Benfords Law for Fraud Detection[J].Internal Auditing,2004,19(1):4-9.
[4] CINDY D,WILLIAM H,CARL P. The Effective Use of Benfords Law to Assist in Detecting Fraud in Accounting Data[J]. Journal of Forensic Accounting, 2004(5):1524-1586.
[5] NIGRINI M J. I've Got Your Number[J]. Journal of Accountancy,1999,187(5).
[6] NIGRINI M J. Digital Analysis using Benfords Law: Tests and Statistics for auditor[J]. EDPACS,2001,28(9):1-2.
[7] DRAKE P D,NIGRINI M J. Computer assisted analytical procedures using Benfords Law[J]. Journal of Accounting Education,2000,18(2):127-146.
[8] 张苏彤,奔福德定律:一种舞弊审计的数值分析方法[J].中国注册会计师,2005(11):70-72.
[9] 张苏彤,康智慧.信息时代舞弊审计新工具——奔福德定律及其来自中国上市公司的实证测试[J].审计研究,2007(3):81-87.
[10] 王福胜,李勋,孙逊.奔福德定律及其在审计中的应用研究[J].财会通讯(综合版),2007(3):13-16.
[11] 朱文明,王昊,陈伟.基于Benford 法则的舞弊检测方法研究[J].数理统计与管理,2007,26(1):41-46.
[12] 许存兴,张芙蓉.上市公司资产负债表造假实证分析——基于奔福德定律的研究[J].内蒙古财经学院学报,2009(3):65-69.
[13] 许存兴,张芙蓉.上市公司财务舞弊实证分析[J].天津商业大学学报,2010(3):51-54.
[14] ROGER S P. On the distribution of the first significant digits[J]. Annals of Mathematical Statistics, 1961,32(4):1223-1230.
[15] NIGRINI M J. Taxpayer compliance application of Benfords law[J]. Journal of the American Taxation Association,1996,18(1).
[16] NIGRINI M J,MITTERMAIER L I. The Use of Benford's Law as an Aid in Analytical Procedures[J]. Auditing:A Journal of Practice & Theory,1997,16(2):52-67.
[17] BASSAM H. Assessing Data Authenticity with Benford's Law[J].Information Systems Control Journal,2002(6):41.
[18] RAIMI R A. The first digit problem[J]. American Mathematical Monthly,1976,83(7):521-538.
